4.2指数函数 课件(共32张PPT)
文档属性
| 名称 | 4.2指数函数 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-09 00:00:00 | ||
图片预览










文档简介
(共32张PPT)
由已知式,求正数m的值:
(1) (2) (3)
答案:
幂
x的取值范围是什么?
R
函数
指数函数
什么函数?
问题1.
复习引入
问题2.《庄子·天下篇》中写道:
“一尺之棰,日取之半,万世不竭”
情景导学
...
一尺之棰 日取其半
第1天后
第2天后
第3天后
第4天后
第x天后
截取 x 天后,木棰的剩余量 y 与 x 所满足的关系式
...
杭州国庆期间的堵车画面
问题3.随着人民生活水平的提高,汽车的使用也越来越普遍,根据2018年发改委发布的《未来我国汽车需求分析报告》判断,今后汽车需求量的年平均增长率预计可达到 7% .那么以后各年汽车需求量将是2018年的多少倍?
分析: 如果把我国2018年汽车需求量看成是1个单位,2019年为第一年,那么:
1年后(即2019年),我国的汽车需求量可望为2018年的(1+7℅)倍;
2年后(即2020年),我国的汽车需求量可望为2019年的(1+7℅)2倍;
……
设x年后我国的汽车需求量为2018年的y倍,那么
像这样,增长率为常数的变化方式,我们称为指数增长.
杭州车牌摇号、车辆限行
问题4.课桌椅的更换,折旧问题.
爱护公物,人人有责!
爱护公共设施,提高自我修养!
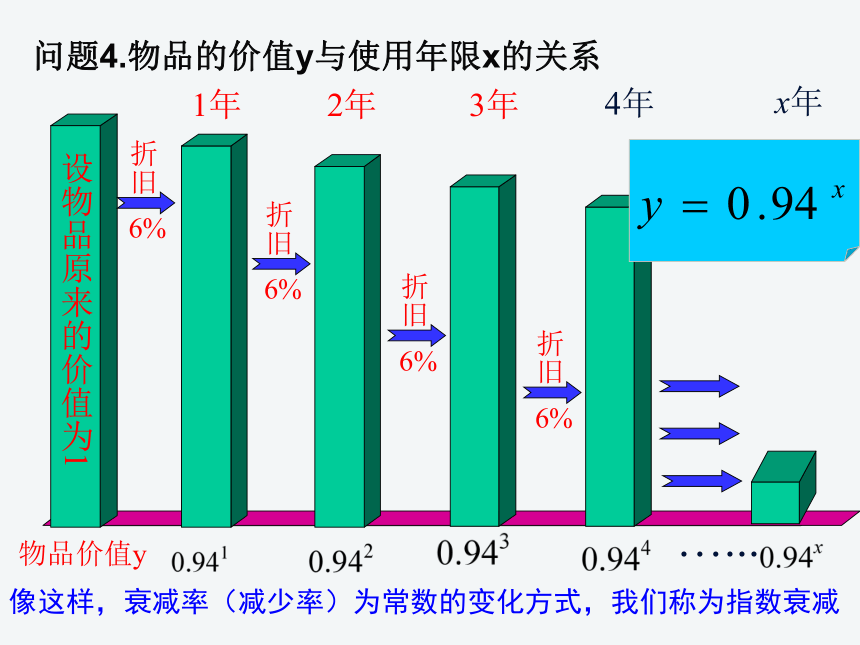
设物品原来的价值为1
x年
…...
折旧
6%
折旧
6%
折旧
6%
折旧
6%
1年
2年
3年
4年
问题4.物品的价值y与使用年限x的关系
物品价值y
像这样,衰减率(减少率)为常数的变化方式,我们称为指数衰减
上述问题中的函数解析式有什么共同特征?
问题 解析式 共同特征
问题1
问题2 问题3 问题4 探究
指数幂形式
自变量在指数位置
底数是常量
指数函数一般形式
其中
是自变量.
学习新知
指数函数
的定义域是什么
思考
为了使y=ax对任意的实数x都有意义,必须有a>0.
R
(a>0且a≠1)
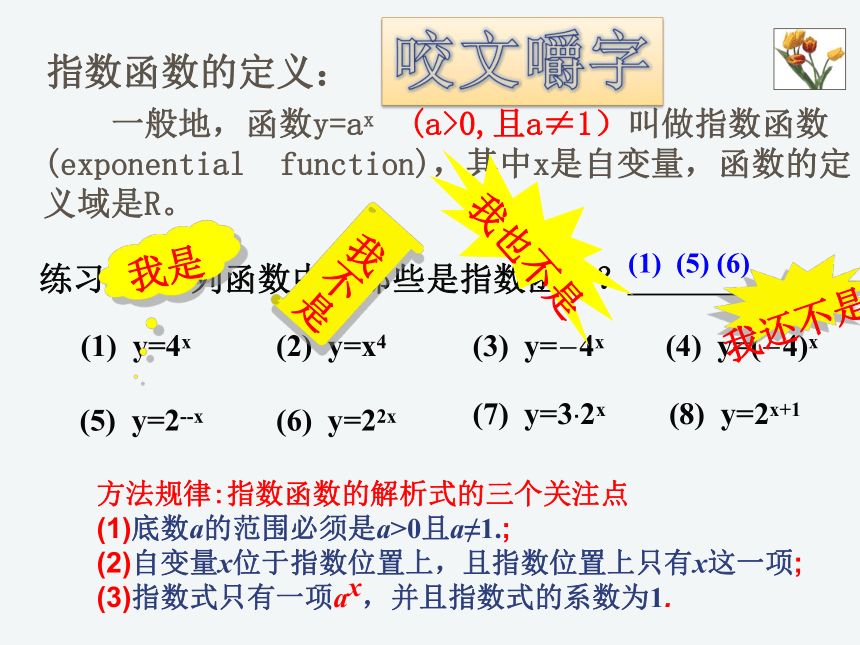
指数函数的定义:
一般地,函数y=ax (a>0,且a≠1)叫做指数函数
(exponential function),其中x是自变量,函数的定
义域是R。
问题:a的取值有哪几个区间
0
1
a
有(0,1)和(1,+∞)两个区间.
1常常成为讨论(分类)时的界值.
指数函数的定义:
一般地,函数y=ax (a>0,且a≠1)叫做指数函数
(exponential function),其中x是自变量,函数的定
义域是R。
练习1:下列函数中,那些是指数函数? .
(1) (5) (6)
(1) y=4x
(2) y=x4
(3) y=-4x
(4) y=(-4)x
(8) y=2x+1
(6) y=22x
(7) y=3·2x
(5) y=2--x
方法规律:指数函数的解析式的三个关注点
(1)底数a的范围必须是a>0且a≠1.;
(2)自变量x位于指数位置上,且指数位置上只有x这一项;
(3)指数式只有一项ax,并且指数式的系数为1.
我是
我不是
我也不是
我还不是
咬文嚼字
例1.指数函数 的图象经过点 ,求
待定系数法
研究函数的一般思路:
研究函数的一般方法是:
函数的
图象
函数的
性质
特殊的
函数
函数的
定义
用性质
解问题
探求新知
画出指数函数y=ax (a>0,且a≠1)的图象.
作出 , 的函数图像.
从特殊到一般
列表 描点 连线
-2 -1.5 -1 -0.5 0 0.5 1 1.5 2
作出函数 的图象
0
1
1
.
.
.
.
.
.
.
.
.
0.35
0.25
0. 71
4
2
2.83
1
1.41
0.5
…
…
…
…
-2 -1.5 -1 -0.5 0 0.5 1 1.5 2
4 2.83 2 1.41 1 0.71 0.5 0.35 0.25
作出函数 的图象
0
1
1
.
.
.
.
.
.
.
.
.
…
…
…
…
x y
… …
-3 0.125
-2 0.25
-1 0.5
0 1
1 2
2 4
3 8
… …
x y
… …
-3 8
-2 4
-1 2
0 1
1 0.5
2 0.25
3 0.125
… …
同一坐标系下指数函数 和 的图象有什么关系?
两个函数图象关于y 轴对称
作出 , 的函数图像.
O
1
1
关于y轴对称
描点、连线
0
1
1
0
1
1
0
1
0
1
y=ax (0y=ax (a>1)
X
O
Y
y=1
y=3X
y = 2 x
观察右边图象,回答下列问题:
问题1.图象分别在哪几个象限?
问题2.图象的上升、下降与底数a有联系吗?
问题3.图象中有哪些特殊的点?
答:当底数__时图象上升;当底数____时图象下降.
一、二
底数a由大变小时函数图像在第一象限内按___时针方向旋转.
顺
向上无限伸展,向下与x轴无限接近
图象还有其他哪些特征
向上无限伸展,直冲云霄
向下无限接近,直逼地面
天
地
指数函数的图象和性质
a>1 0图 象
x
y
0
y=1
y=ax
(a>1)
(0,1)
y
0
(0x
y=1
y=ax
(0,1)
a>1 0图 象 特 征
a>1 0性 质
1.图象全在x轴上方,与x轴无限接近
1.定义域为R,值域为(0,+ ).
2.图象过定点(0,1)
2.当x=0时,y=1
3.自左向右图象逐渐上升
3.自左向右图象逐渐下降
3.在R上是增函数
3.在R上是减函数
4.图象分布在左下和右上两个区域内
4.图象分布在左上和右下两个区域内
4.当x>0时,y>1;当x<0时,04.当x>0时, 01.
解锁密钥:
指数函数很简单
一瞥一捺记心间
图像恒过(0,1)点
横轴就是渐近线
是增是减观底数
y
x
O
y=1.5x
1
例2.比较下列各组数中两个值的大小:
(1)1.52.5,1.53.2;
解:(1)考察指数函数y=1.5x.
因为1. 5>1
所以y=1.5 x在R上是单调递增函数,
又因为 2. 5<3.2
所以1.52.5<1.53.2.
1.52.5
1.53.2
2.5
3.2
(2)0.5-1.2,0.5-1.5;
同底比较大小
构造一个指数函数,利用函数单调性
解:
例2.比较下列各组数中两个值的大小:
解:由指数函数的性质知
1.5 0.3> 1.5 0=1
所以
1.50.3>0.81.2.
0.8 1.2< 0.8 0=1
例2.比较下列各组数中两个值的大小:
(4)1.50.3,0.81.2.
y
x
O
y=1.5x
1
y=0.8x
寻找中间量
0.3
1.2
B
一箭多雕
变式2
≥
≥
≥
3.当底数不同不能直接比较时:可借助中间
数(如1或0等),间接比较两个指数的大小.
总结:
1.当同底数并明确底数a 与1的大小关系时:
直接用函数的单调性来解;
2. 当同底数但不明确底数a与1的大小关系时: 要分情况讨论;
应用
体会两个函数y=(0.99)x与y=(1.01)x
举例:
约为0.0255与37.7834
365天的飞跃
这就是:差之毫厘,谬以千里。
因此平时要防微杜渐,
莫以善小而不为,莫以恶小而为之。
假如每天进步一点点,日积月累,积极向前,那么成果是显然的。但如果每天懒散一点、懈怠一点呢?
知
识
升
华
知识上
方法上
归纳总结
(一)指数函数的定义;
(二)图象及性质;
(三)图象及性质的应用.
(一)分类讨论;
(二)数形结合;
(三)特殊到一般.
刺破青天锷未残,
接近地面趋无限;
百朵菊花集一束,
愿将芬芳留人间.
刀剑的刃
1.01x意指,每天改變或學習一點點,最後也將聚少成多聚沙成塔。
0.99x意指,每天偷懶一點,損失在不知不覺中變大,競爭力也在不知不覺中消失。
希望大家都能像那1.01x的數學題一般成功幸福!!!
由已知式,求正数m的值:
(1) (2) (3)
答案:
幂
x的取值范围是什么?
R
函数
指数函数
什么函数?
问题1.
复习引入
问题2.《庄子·天下篇》中写道:
“一尺之棰,日取之半,万世不竭”
情景导学
...
一尺之棰 日取其半
第1天后
第2天后
第3天后
第4天后
第x天后
截取 x 天后,木棰的剩余量 y 与 x 所满足的关系式
...
杭州国庆期间的堵车画面
问题3.随着人民生活水平的提高,汽车的使用也越来越普遍,根据2018年发改委发布的《未来我国汽车需求分析报告》判断,今后汽车需求量的年平均增长率预计可达到 7% .那么以后各年汽车需求量将是2018年的多少倍?
分析: 如果把我国2018年汽车需求量看成是1个单位,2019年为第一年,那么:
1年后(即2019年),我国的汽车需求量可望为2018年的(1+7℅)倍;
2年后(即2020年),我国的汽车需求量可望为2019年的(1+7℅)2倍;
……
设x年后我国的汽车需求量为2018年的y倍,那么
像这样,增长率为常数的变化方式,我们称为指数增长.
杭州车牌摇号、车辆限行
问题4.课桌椅的更换,折旧问题.
爱护公物,人人有责!
爱护公共设施,提高自我修养!
设物品原来的价值为1
x年
…...
折旧
6%
折旧
6%
折旧
6%
折旧
6%
1年
2年
3年
4年
问题4.物品的价值y与使用年限x的关系
物品价值y
像这样,衰减率(减少率)为常数的变化方式,我们称为指数衰减
上述问题中的函数解析式有什么共同特征?
问题 解析式 共同特征
问题1
问题2 问题3 问题4 探究
指数幂形式
自变量在指数位置
底数是常量
指数函数一般形式
其中
是自变量.
学习新知
指数函数
的定义域是什么
思考
为了使y=ax对任意的实数x都有意义,必须有a>0.
R
(a>0且a≠1)
指数函数的定义:
一般地,函数y=ax (a>0,且a≠1)叫做指数函数
(exponential function),其中x是自变量,函数的定
义域是R。
问题:a的取值有哪几个区间
0
1
a
有(0,1)和(1,+∞)两个区间.
1常常成为讨论(分类)时的界值.
指数函数的定义:
一般地,函数y=ax (a>0,且a≠1)叫做指数函数
(exponential function),其中x是自变量,函数的定
义域是R。
练习1:下列函数中,那些是指数函数? .
(1) (5) (6)
(1) y=4x
(2) y=x4
(3) y=-4x
(4) y=(-4)x
(8) y=2x+1
(6) y=22x
(7) y=3·2x
(5) y=2--x
方法规律:指数函数的解析式的三个关注点
(1)底数a的范围必须是a>0且a≠1.;
(2)自变量x位于指数位置上,且指数位置上只有x这一项;
(3)指数式只有一项ax,并且指数式的系数为1.
我是
我不是
我也不是
我还不是
咬文嚼字
例1.指数函数 的图象经过点 ,求
待定系数法
研究函数的一般思路:
研究函数的一般方法是:
函数的
图象
函数的
性质
特殊的
函数
函数的
定义
用性质
解问题
探求新知
画出指数函数y=ax (a>0,且a≠1)的图象.
作出 , 的函数图像.
从特殊到一般
列表 描点 连线
-2 -1.5 -1 -0.5 0 0.5 1 1.5 2
作出函数 的图象
0
1
1
.
.
.
.
.
.
.
.
.
0.35
0.25
0. 71
4
2
2.83
1
1.41
0.5
…
…
…
…
-2 -1.5 -1 -0.5 0 0.5 1 1.5 2
4 2.83 2 1.41 1 0.71 0.5 0.35 0.25
作出函数 的图象
0
1
1
.
.
.
.
.
.
.
.
.
…
…
…
…
x y
… …
-3 0.125
-2 0.25
-1 0.5
0 1
1 2
2 4
3 8
… …
x y
… …
-3 8
-2 4
-1 2
0 1
1 0.5
2 0.25
3 0.125
… …
同一坐标系下指数函数 和 的图象有什么关系?
两个函数图象关于y 轴对称
作出 , 的函数图像.
O
1
1
关于y轴对称
描点、连线
0
1
1
0
1
1
0
1
0
1
y=ax (0
X
O
Y
y=1
y=3X
y = 2 x
观察右边图象,回答下列问题:
问题1.图象分别在哪几个象限?
问题2.图象的上升、下降与底数a有联系吗?
问题3.图象中有哪些特殊的点?
答:当底数__时图象上升;当底数____时图象下降.
一、二
底数a由大变小时函数图像在第一象限内按___时针方向旋转.
顺
向上无限伸展,向下与x轴无限接近
图象还有其他哪些特征
向上无限伸展,直冲云霄
向下无限接近,直逼地面
天
地
指数函数的图象和性质
a>1 0
x
y
0
y=1
y=ax
(a>1)
(0,1)
y
0
(0
y=1
y=ax
(0,1)
a>1 0
a>1 0
1.图象全在x轴上方,与x轴无限接近
1.定义域为R,值域为(0,+ ).
2.图象过定点(0,1)
2.当x=0时,y=1
3.自左向右图象逐渐上升
3.自左向右图象逐渐下降
3.在R上是增函数
3.在R上是减函数
4.图象分布在左下和右上两个区域内
4.图象分布在左上和右下两个区域内
4.当x>0时,y>1;当x<0时,0
解锁密钥:
指数函数很简单
一瞥一捺记心间
图像恒过(0,1)点
横轴就是渐近线
是增是减观底数
y
x
O
y=1.5x
1
例2.比较下列各组数中两个值的大小:
(1)1.52.5,1.53.2;
解:(1)考察指数函数y=1.5x.
因为1. 5>1
所以y=1.5 x在R上是单调递增函数,
又因为 2. 5<3.2
所以1.52.5<1.53.2.
1.52.5
1.53.2
2.5
3.2
(2)0.5-1.2,0.5-1.5;
同底比较大小
构造一个指数函数,利用函数单调性
解:
例2.比较下列各组数中两个值的大小:
解:由指数函数的性质知
1.5 0.3> 1.5 0=1
所以
1.50.3>0.81.2.
0.8 1.2< 0.8 0=1
例2.比较下列各组数中两个值的大小:
(4)1.50.3,0.81.2.
y
x
O
y=1.5x
1
y=0.8x
寻找中间量
0.3
1.2
B
一箭多雕
变式2
≥
≥
≥
3.当底数不同不能直接比较时:可借助中间
数(如1或0等),间接比较两个指数的大小.
总结:
1.当同底数并明确底数a 与1的大小关系时:
直接用函数的单调性来解;
2. 当同底数但不明确底数a与1的大小关系时: 要分情况讨论;
应用
体会两个函数y=(0.99)x与y=(1.01)x
举例:
约为0.0255与37.7834
365天的飞跃
这就是:差之毫厘,谬以千里。
因此平时要防微杜渐,
莫以善小而不为,莫以恶小而为之。
假如每天进步一点点,日积月累,积极向前,那么成果是显然的。但如果每天懒散一点、懈怠一点呢?
知
识
升
华
知识上
方法上
归纳总结
(一)指数函数的定义;
(二)图象及性质;
(三)图象及性质的应用.
(一)分类讨论;
(二)数形结合;
(三)特殊到一般.
刺破青天锷未残,
接近地面趋无限;
百朵菊花集一束,
愿将芬芳留人间.
刀剑的刃
1.01x意指,每天改變或學習一點點,最後也將聚少成多聚沙成塔。
0.99x意指,每天偷懶一點,損失在不知不覺中變大,競爭力也在不知不覺中消失。
希望大家都能像那1.01x的數學題一般成功幸福!!!
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
