人教版八年级上册数学 11.1.2 三角形的高、中线与角平分线 学案(无答案)
文档属性
| 名称 | 人教版八年级上册数学 11.1.2 三角形的高、中线与角平分线 学案(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 113.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-10 15:34:14 | ||
图片预览

文档简介
三角形的高、中线与角平分线
【学习目标】
1.了解三角形的高、中线、角平分线。
2.会画三角形的高、中线、角平分线。
【学习重难点】
1.三角形的高、中线与角平分线的特征。
2.钝角三角形高的画法。
【学习过程】
一、复习回顾。
1.六边形的内角和等于_____度。
2.一个多边形的每一个外角为36°,那么这个多边形的边数是_____。
3.正八边形的每一个内角=_____,每一个外角=_____,每一个内角都比一个外角大_____度。
4.如果一个多边形的内角和是1800°,则这个多边形是_____边形。
二、新课学习。
(一)三角形的高、中线、角平分线。
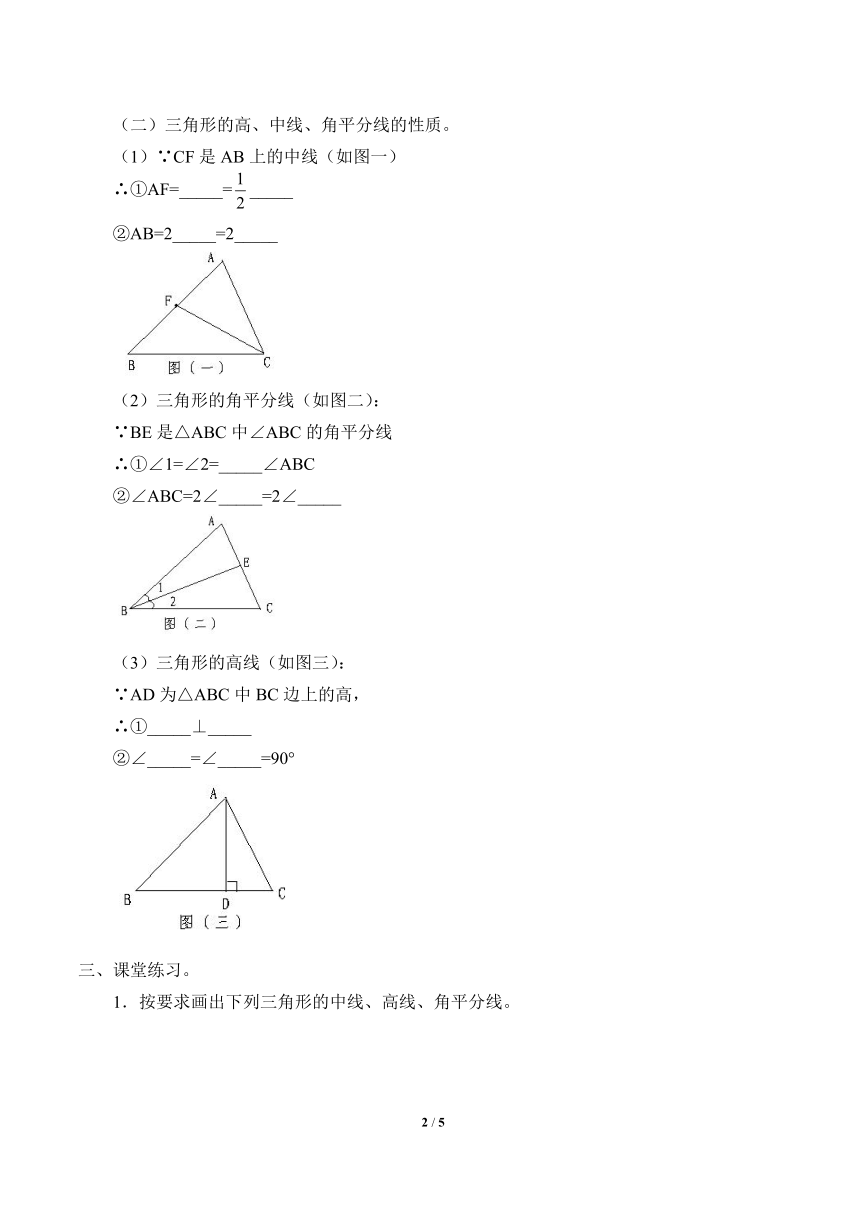
探究:请在下图三角形中,分别画出:
(1)BC边上的高AD;(2)BC边上的中线AE;(3)∠BAC平分线AF。
提示:
①画“BC边上的高AD”就是“过顶点_____向_____边上作垂线”。
②画“BC边上的中线AE”就是“连接顶点_____和_____边上的中点”。
若画三角形ABC的三条中线相交于一点,三条中线的焦点叫做三角形的_____。
③画“∠BAC平分线AF”就是“交∠BAC所对的边BC于点F”。
(二)三角形的高、中线、角平分线的性质。
(1)∵CF是AB上的中线(如图一)
∴①AF=_____=_____
②AB=2_____=2_____
(2)三角形的角平分线(如图二):
∵BE是△ABC中∠ABC的角平分线
∴①∠1=∠2=_____∠ABC
②∠ABC=2∠_____=2∠_____
(3)三角形的高线(如图三):
∵AD为△ABC中BC边上的高,
∴①_____⊥_____
②∠_____=∠_____=90°
三、课堂练习。
1.按要求画出下列三角形的中线、高线、角平分线。
2.如图1:∠BAC=60°,AD是三角形ABC的角平分线,则∠BAD=_____°,∠CAD=_____°。
3.如图,AD为△ABC中BC边上的高,∠B=35°,∠C=45°,
则∠BDA=_____°∠BAD=_____°,∠CAD=_____°。
4.如图,△ABC的周长为20,AB=6,AC=8,AD是BC边上的中线,则BC=_____,BD=_____,CD=_____。
5.关于三角形的高,下列说法正确的是( )。
A.必在三角形的内部 B.必在三角形的外部
C.必和三角形的一条边重合 D.以上均有可能
6.填空。
(1)如图,AD,BE,CF是的三条中线,
其中AF=3.5cm,CD=3cm,AC=4cm,
则AB=_____cm,BD=_____cm,AE=_____cm。
(2)如图,AD,BE,CF是的三条角平分线,
其中∠2=30°,∠ABC=70°,∠4=25°,
则,,。
7.如图,AD⊥BC,∠1=∠2,∠C=65°,求的各内角的度数。
8.如图,AD是中BC边上的中线,△ABD的周长比△ACD的周长大3cm,AB=8cm,则AC=______。
9.已知等腰三角形ABC,AB=AC,BD是AC边上的中线,BD把△ABC的周长分为15和12两部分,求△ABC各边的长。
4 / 4
【学习目标】
1.了解三角形的高、中线、角平分线。
2.会画三角形的高、中线、角平分线。
【学习重难点】
1.三角形的高、中线与角平分线的特征。
2.钝角三角形高的画法。
【学习过程】
一、复习回顾。
1.六边形的内角和等于_____度。
2.一个多边形的每一个外角为36°,那么这个多边形的边数是_____。
3.正八边形的每一个内角=_____,每一个外角=_____,每一个内角都比一个外角大_____度。
4.如果一个多边形的内角和是1800°,则这个多边形是_____边形。
二、新课学习。
(一)三角形的高、中线、角平分线。
探究:请在下图三角形中,分别画出:
(1)BC边上的高AD;(2)BC边上的中线AE;(3)∠BAC平分线AF。
提示:
①画“BC边上的高AD”就是“过顶点_____向_____边上作垂线”。
②画“BC边上的中线AE”就是“连接顶点_____和_____边上的中点”。
若画三角形ABC的三条中线相交于一点,三条中线的焦点叫做三角形的_____。
③画“∠BAC平分线AF”就是“交∠BAC所对的边BC于点F”。
(二)三角形的高、中线、角平分线的性质。
(1)∵CF是AB上的中线(如图一)
∴①AF=_____=_____
②AB=2_____=2_____
(2)三角形的角平分线(如图二):
∵BE是△ABC中∠ABC的角平分线
∴①∠1=∠2=_____∠ABC
②∠ABC=2∠_____=2∠_____
(3)三角形的高线(如图三):
∵AD为△ABC中BC边上的高,
∴①_____⊥_____
②∠_____=∠_____=90°
三、课堂练习。
1.按要求画出下列三角形的中线、高线、角平分线。
2.如图1:∠BAC=60°,AD是三角形ABC的角平分线,则∠BAD=_____°,∠CAD=_____°。
3.如图,AD为△ABC中BC边上的高,∠B=35°,∠C=45°,
则∠BDA=_____°∠BAD=_____°,∠CAD=_____°。
4.如图,△ABC的周长为20,AB=6,AC=8,AD是BC边上的中线,则BC=_____,BD=_____,CD=_____。
5.关于三角形的高,下列说法正确的是( )。
A.必在三角形的内部 B.必在三角形的外部
C.必和三角形的一条边重合 D.以上均有可能
6.填空。
(1)如图,AD,BE,CF是的三条中线,
其中AF=3.5cm,CD=3cm,AC=4cm,
则AB=_____cm,BD=_____cm,AE=_____cm。
(2)如图,AD,BE,CF是的三条角平分线,
其中∠2=30°,∠ABC=70°,∠4=25°,
则,,。
7.如图,AD⊥BC,∠1=∠2,∠C=65°,求的各内角的度数。
8.如图,AD是中BC边上的中线,△ABD的周长比△ACD的周长大3cm,AB=8cm,则AC=______。
9.已知等腰三角形ABC,AB=AC,BD是AC边上的中线,BD把△ABC的周长分为15和12两部分,求△ABC各边的长。
4 / 4
