人教版八年级上册数学11.3.2 多边形的内角和 学案(含答案)
文档属性
| 名称 | 人教版八年级上册数学11.3.2 多边形的内角和 学案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 147.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-10 16:56:43 | ||
图片预览


文档简介
多边形的内角和
班级: 组号: 姓名:
一、旧知回顾
1.三角形的内角和等于 度;正方形、长方形的内角和等于 度。
2.从n边形的一个顶点出发,可以画 条对角线,这些对角线把这个n边形分割成 个三角形。
二、新知梳理
3.认真阅读理解P21-22中关于多边形内角和推理过程。
4.多边形的内角和定理:n边形的内角和等于 度。
5.认真阅读P23中关于多边形外角和的推理过程。
6.多边形的外角和定理:多边形的外角和等于 度。
7.从P21-22多边形外角和的推理过程思路,你应该可以得出另一种证明多边形的内角和定理的方法。画出示意图,进行适当的推理说明。
三、试一试
8.填空:
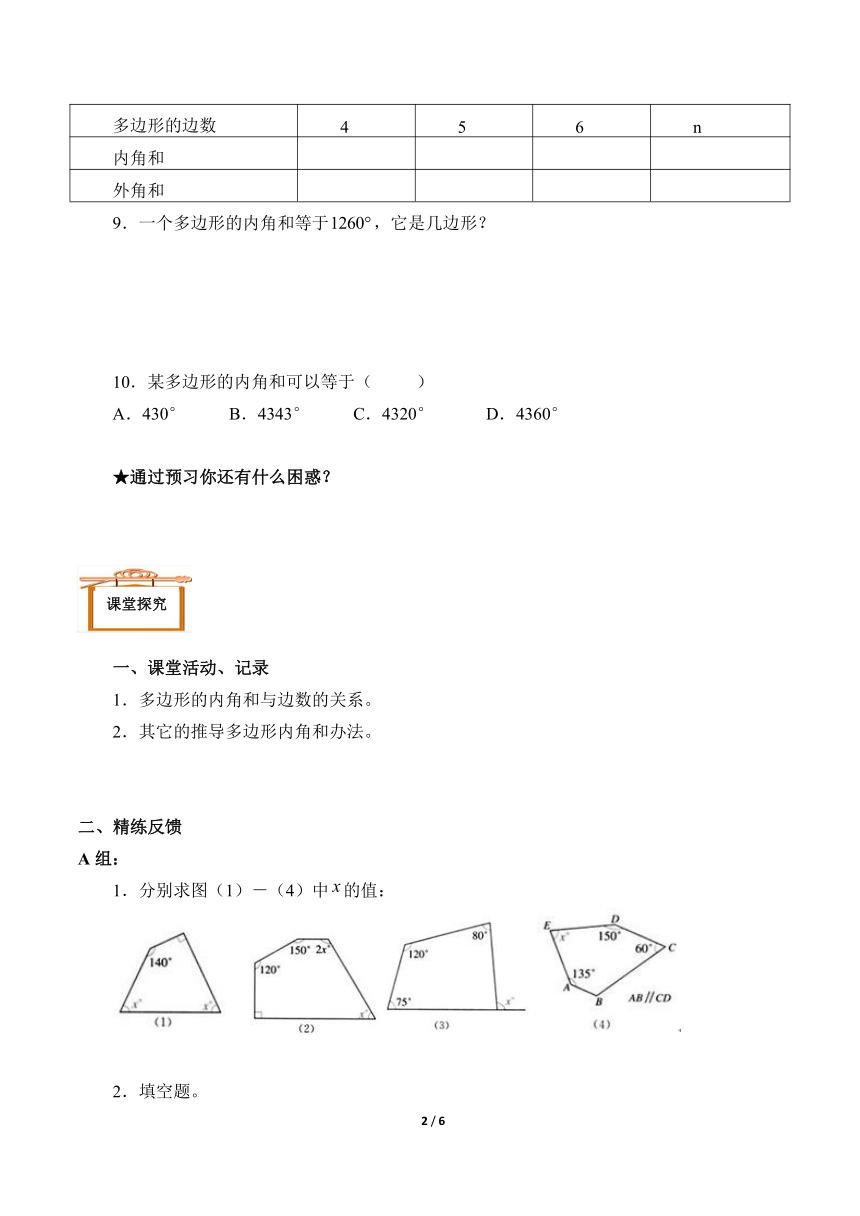
多边形的边数 4 5 6 n
内角和
外角和
9.一个多边形的内角和等于,它是几边形?
10.某多边形的内角和可以等于( )
A.430° B.4343° C.4320° D.4360°
★通过预习你还有什么困惑?
一、课堂活动、记录
1.多边形的内角和与边数的关系。
2.其它的推导多边形内角和办法。
二、精练反馈
A组:
1.分别求图(1)-(4)中的值:
2.填空题。
(1)内角和为1440°的多边形是 。
(2)一个多边形的每一个外角都等于30°,则这个多边形为 边形。
(3)一个多边形的每个内角都等于135°,则这个多边形为 边形。
(4)内角和等于外角和的多边形是 边形。
3.计算正十边形的每个内角的度数。
B组:
4.如图,五边形ABCDE的内角都相等,且,,求的值。
三、课堂小结
1.多边形内角和等于(n-2)×180。
2.如果一个四边形的一组对角互补,那么另一组对角也互补。
3.多边形外角和等于360。
四、拓展延伸(选做题)
1.一个多边形的内角和是外角和的2倍,它是 边形。
2.n边形的内角和与外角和比为13:2,则n= 。
3.一个多边形少一个内角的度数和为2300°。
(1)求它的边数;
(2)求少的那个内角的度数。
4.如果一个凸多边形的所有内角从小到大排列起来,恰好依次增加的度数相同,设该凸多边形的最小内角的度数为100°,最大内角的度数为140°,求该凸多边形的边数。
【答案】
【学前准备】
1.180 360
2.(n-3) (n-2)
3.略
4.180*(n-2)
5.略
6.360°
7.略
8.
多边形的边数 4 5 6 n
内角和 360 540 720 180(n-2)
外角和 360 360 360 360
9.解:设这个多边形为n边形
180(n-2)=1260
n=9
10.C
【课堂探究】
课堂活动、记录
略
精练反馈
1.x=65° x=60° x=95° x=75°
2.(1)十 (2)十二 (3)八 (4)四
3.解;设正十边形每个内角度数为x
10x=180°(10-2)
x=144°
4.解:因为五边形的内角和是540°,则每个内角为540°÷5=108°,∴∠E=∠C=108°,又∵∠1=∠2,∠3=∠4,由三角形内角和定理可知,∠1=∠2=∠3=∠4=(180°-108°)÷2=36°,∴x=∠EDC-∠1-∠3=108°-36°-36°=36°。
课堂小结
略
拓展延伸
1.六
2.十五
3.略
4.略
5 / 6
班级: 组号: 姓名:
一、旧知回顾
1.三角形的内角和等于 度;正方形、长方形的内角和等于 度。
2.从n边形的一个顶点出发,可以画 条对角线,这些对角线把这个n边形分割成 个三角形。
二、新知梳理
3.认真阅读理解P21-22中关于多边形内角和推理过程。
4.多边形的内角和定理:n边形的内角和等于 度。
5.认真阅读P23中关于多边形外角和的推理过程。
6.多边形的外角和定理:多边形的外角和等于 度。
7.从P21-22多边形外角和的推理过程思路,你应该可以得出另一种证明多边形的内角和定理的方法。画出示意图,进行适当的推理说明。
三、试一试
8.填空:
多边形的边数 4 5 6 n
内角和
外角和
9.一个多边形的内角和等于,它是几边形?
10.某多边形的内角和可以等于( )
A.430° B.4343° C.4320° D.4360°
★通过预习你还有什么困惑?
一、课堂活动、记录
1.多边形的内角和与边数的关系。
2.其它的推导多边形内角和办法。
二、精练反馈
A组:
1.分别求图(1)-(4)中的值:
2.填空题。
(1)内角和为1440°的多边形是 。
(2)一个多边形的每一个外角都等于30°,则这个多边形为 边形。
(3)一个多边形的每个内角都等于135°,则这个多边形为 边形。
(4)内角和等于外角和的多边形是 边形。
3.计算正十边形的每个内角的度数。
B组:
4.如图,五边形ABCDE的内角都相等,且,,求的值。
三、课堂小结
1.多边形内角和等于(n-2)×180。
2.如果一个四边形的一组对角互补,那么另一组对角也互补。
3.多边形外角和等于360。
四、拓展延伸(选做题)
1.一个多边形的内角和是外角和的2倍,它是 边形。
2.n边形的内角和与外角和比为13:2,则n= 。
3.一个多边形少一个内角的度数和为2300°。
(1)求它的边数;
(2)求少的那个内角的度数。
4.如果一个凸多边形的所有内角从小到大排列起来,恰好依次增加的度数相同,设该凸多边形的最小内角的度数为100°,最大内角的度数为140°,求该凸多边形的边数。
【答案】
【学前准备】
1.180 360
2.(n-3) (n-2)
3.略
4.180*(n-2)
5.略
6.360°
7.略
8.
多边形的边数 4 5 6 n
内角和 360 540 720 180(n-2)
外角和 360 360 360 360
9.解:设这个多边形为n边形
180(n-2)=1260
n=9
10.C
【课堂探究】
课堂活动、记录
略
精练反馈
1.x=65° x=60° x=95° x=75°
2.(1)十 (2)十二 (3)八 (4)四
3.解;设正十边形每个内角度数为x
10x=180°(10-2)
x=144°
4.解:因为五边形的内角和是540°,则每个内角为540°÷5=108°,∴∠E=∠C=108°,又∵∠1=∠2,∠3=∠4,由三角形内角和定理可知,∠1=∠2=∠3=∠4=(180°-108°)÷2=36°,∴x=∠EDC-∠1-∠3=108°-36°-36°=36°。
课堂小结
略
拓展延伸
1.六
2.十五
3.略
4.略
5 / 6
