人教版初中数学八年级上册 第十一章三角形复习 教案
文档属性
| 名称 | 人教版初中数学八年级上册 第十一章三角形复习 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 120.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-10 19:45:49 | ||
图片预览

文档简介
《三角形》复习课教学设计6
一、教学目的
复习三角形有关的概念,等腰三角形、直角三角形的性质及判定定理;能根据给出的图形和条件准确说出相关的结论,熟练运用三角形有关定义和定理解答简单数学问题。
二、教学内容
三角形的有关定义和定理,等腰三角形、直角三角形的性质及判定定理
(
引入
学生练习
课堂检测
)三、教学流程
四、教学手段:老师精讲,以学生练习、讨论为主;PPT展示
五、教学过程
(一)引入本节课的复习内容,《三角形》考题类型。计划用时2分钟
(二)学生练习
一、三角形的边、角关系
考点内容 考点练习(A)
(1)三角形的边、角关系 ①三角形的任何两边之和大于第三边,任何两边之差小于第三边; ②三角形的内角和等于180 ,外角和等于360 ; ③三角形的一个外角等于与它不相邻的两个内角之和。 (1)已知三角形的两边长分别是4和10,则此三角形第三边的长的取值范围是 ; (2)在△ABC中,∠A=60 , ∠B=70 , 则∠C= ; (3)如图,A、C、D共线, ∠A=30 , ∠B=70 , 则∠BCD= ;
(2)三角形的主要线段 ①三角形的高: ②三角形的角平分线: ③三角形的中线: ④三角形中位线:连接三角形两边的中点的线段叫做三角形的中位线。 ⑤三角形的中位线性质:三角形的中位线平行于第三边且等于第三边的一半。 (4)如图,AD是△ABC的高, ∠B=60 ,∠BAD= ; (5)如图,BD是△ABC的角平分线,若∠1=40 ,∠ABC = 。 (6)如图,△ABC的中线AD, ①若BC=10,则BD= ; ②若BD=10,则BC= 。 (7)如图,D、E分别是AB、AC的中点,若∠B=50 ,BC=10, 则∠ADE= ,DE= 。
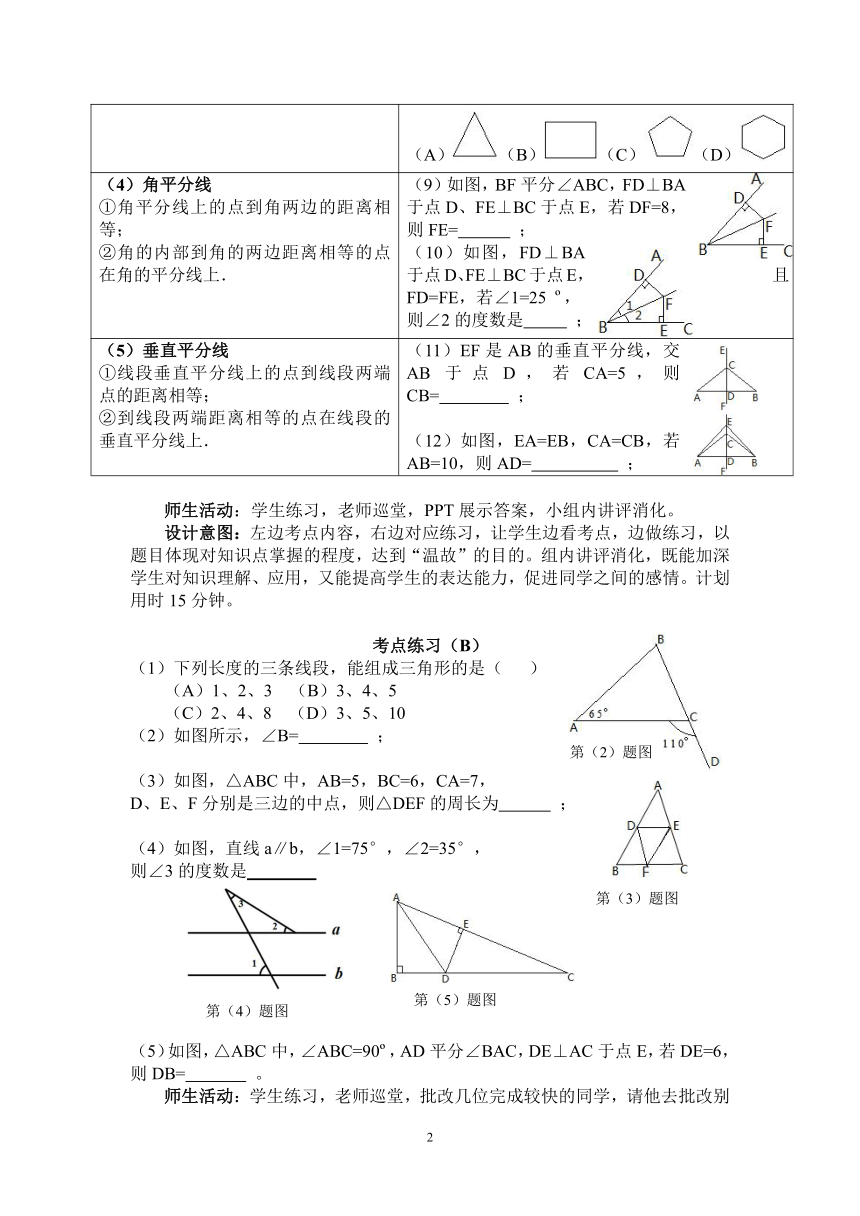
(3)三角形的稳定性 (8)下列各个图形中,那种图形具有稳定性( ) (A)(B)(C)(D)
(4)角平分线 ①角平分线上的点到角两边的距离相等; ②角的内部到角的两边距离相等的点在角的平分线上. (9)如图,BF平分∠ABC,FD⊥BA于点D、FE⊥BC于点E,若DF=8, 则FE= ; (10)如图,FD⊥BA于点D、FE⊥BC于点E,且FD=FE,若∠1=25 , 则∠2的度数是 ;
(5)垂直平分线 ①线段垂直平分线上的点到线段两端点的距离相等; ②到线段两端距离相等的点在线段的垂直平分线上. (11)EF是AB的垂直平分线,交AB于点D,若CA=5,则CB= ; (12)如图,EA=EB,CA=CB,若AB=10,则AD= ;
师生活动:学生练习,老师巡堂,PPT展示答案,小组内讲评消化。
设计意图:左边考点内容,右边对应练习,让学生边看考点,边做练习,以题目体现对知识点掌握的程度,达到“温故”的目的。组内讲评消化,既能加深学生对知识理解、应用,又能提高学生的表达能力,促进同学之间的感情。计划用时15分钟。
(
第(2)题图
)考点练习(B)
(1)下列长度的三条线段,能组成三角形的是( )
(A)1、2、3 (B)3、4、5
(C)2、4、8 (D)3、5、10
(2)如图所示,∠B= ;
(
第(3)题图
)(3)如图,△ABC中,AB=5,BC=6,CA=7,
D、E、F分别是三边的中点,则△DEF的周长为 ;
(4)如图,直线a∥b,∠1=75°,∠2=35°,
则∠3的度数是
(
第(4)题图
) (
第(5)题图
)
(5)如图,△ABC中,∠ABC=90 ,AD平分∠BAC,DE⊥AC于点E,若DE=6,则DB= 。
师生活动:学生练习,老师巡堂,批改几位完成较快的同学,请他去批改别的同学的答案,讲解。PPT展示答案,问同学需要讲评,根据学生的实际,挑1~2题目简单的讲评。
设计意图:经过(A)的练习,(B)是对三角形三边关系等进行一个小检测,巩固三角形三边关系等。计划用时5分钟。
(三)学生练习
二、等腰三角形
考点内容 考点练习(A)
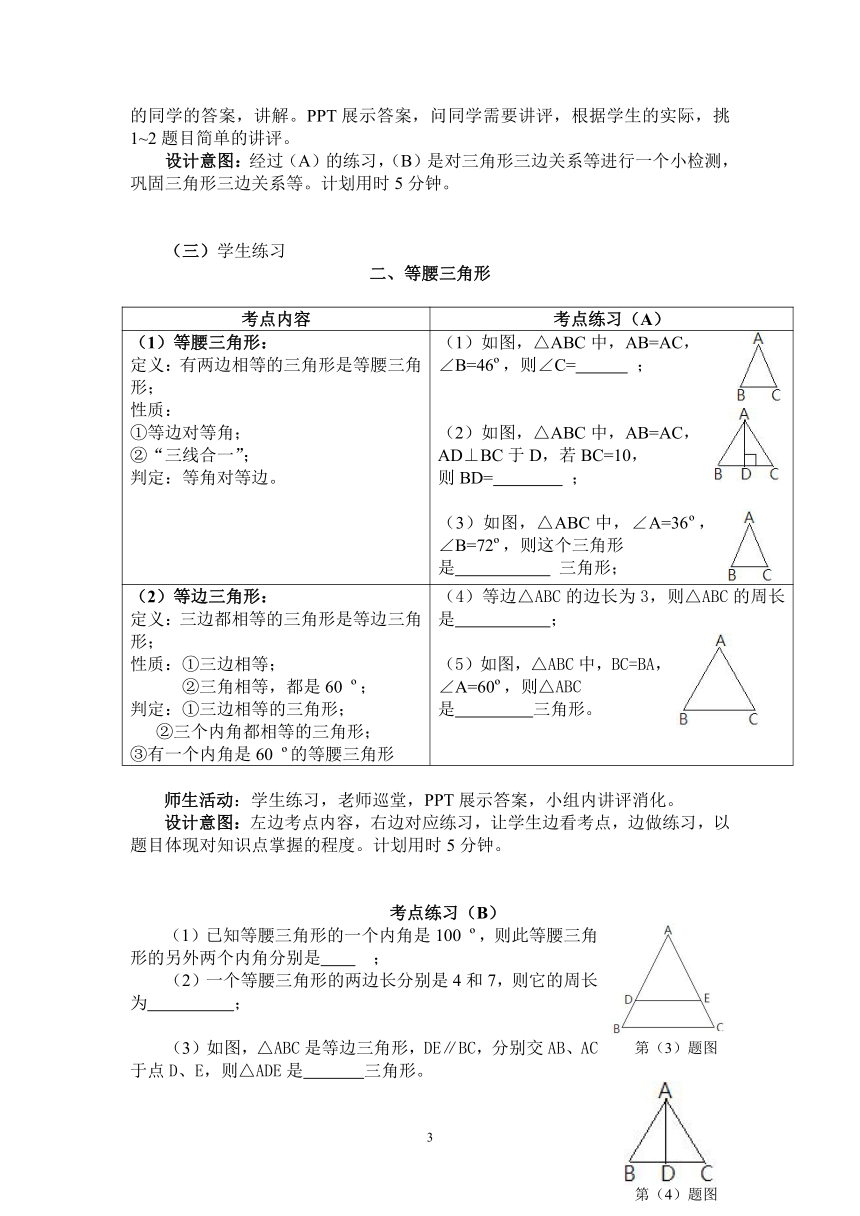
(1)等腰三角形: 定义:有两边相等的三角形是等腰三角形; 性质: ①等边对等角; ②“三线合一”; 判定:等角对等边。 (1)如图,△ABC中,AB=AC, ∠B=46 ,则∠C= ; (2)如图,△ABC中,AB=AC, AD⊥BC于D,若BC=10, 则BD= ; (3)如图,△ABC中,∠A=36 ,∠B=72 ,则这个三角形 是 三角形;
(2)等边三角形: 定义:三边都相等的三角形是等边三角形; 性质:①三边相等; ②三角相等,都是60 ; 判定:①三边相等的三角形; ②三个内角都相等的三角形; ③有一个内角是60 的等腰三角形 (4)等边△ABC的边长为3,则△ABC的周长是 ; (5)如图,△ABC中,BC=BA, ∠A=60 ,则△ABC 是 三角形。
师生活动:学生练习,老师巡堂,PPT展示答案,小组内讲评消化。
设计意图:左边考点内容,右边对应练习,让学生边看考点,边做练习,以题目体现对知识点掌握的程度。计划用时5分钟。
考点练习(B)
(
第(3)题图
)(1)已知等腰三角形的一个内角是100 ,则此等腰三角形的另外两个内角分别是 ;
(2)一个等腰三角形的两边长分别是4和7,则它的周长为 ;
(3)如图,△ABC是等边三角形,DE∥BC,分别交AB、AC于点D、E,则△ADE是 三角形。
(
第(4)题图
)
(4)如图,△ABC中,AB=AC,D是BC的中点,
∠B=50 ,则∠BAD= , ∠BAC= 。
师生活动:学生练习,老师巡堂,批改几位完成较快的同学,请他去批改别的同学的答案,讲解。PPT展示答案,问同学需要讲评,根据学生的实际,挑1~2题目简单的讲评。
设计意图:经过(A)的练习,(B)是对等腰三角形进行一个小检测,巩固等腰三角形的性质与判定。计划用时5分钟。
(四)学生练习
三、直角三角形
考点内容 考点练习(A)
(1)直角三角形 ①直角三角形的两个锐角互余; ②直角三角形中30 角所对的直角边是斜边的一半; ③直角三角形中,斜边上的中线等于斜边的一半; ④勾股定理:直角三角形中,两直角边的平方和等于斜边的平方; ⑤勾股定理逆定理:若一个三角形中有两条边的平方和等于第三边的平方,那么这个三角形是直角三角形。 (1) Rt△ABC中,∠C=90 , ∠A=40 , 则∠B= 。 (2)如图,Rt△ABC中, ∠C=90 ,∠A=30 ,AB=10, 则BC= ; (3)如图,△ABC中, ∠ACB=90 ,D是AB的中点,AB=10, 则CD= ; (4)如图,Rt△ABC中, ∠C=90 ,AC=8,BC=6, 则AB= ; (5)以下各组数为边长,不能组成直角三角形的是( ) (A)2、3、4 (B)3、4、5 (C)10、8、6 (D)5、13、12
师生活动:学生练习,老师巡堂,PPT展示答案,小组内讲评消化。
设计意图:左边考点内容,右边对应练习,让学生边看考点,边做练习,以题目体现对知识点掌握的程度。组内讲评消化。计划用时5分钟。
(
第1、2题图
)
考点练习(B)
(1)如图,Rt△ABC的斜边AB的中线CD=1,则AB的长为 ;
(2)如图,CD是Rt△ABC斜边AB的中线,∠B=30 ,AB=10,则△ACD 的周长是 ;
(3)已知△ABC中,AB=5,BC=12,CA=13, 那么△ABC是( )
(A)锐角三角形 (B)等腰三角形 (C)等边三角形 (D)直角三角形
(4)直角三角形中,一直角边长是6,斜边是10,则另外的一直角边的长是 。
(5)Rt△ABC中,∠C=90 ,∠A=∠B ,则∠B= 。
师生活动:学生练习,老师巡堂,批改几位完成较快的同学,请他去批改别的同学的答案,讲解。PPT展示答案,问同学需要讲评,根据学生的实际,挑1~2题目简单的讲评。
设计意图:经过(A)的练习,(B)是对直角三角形进行一个小检测,巩固直角三角形的性质与判定。计划用时5分钟。
(五)学生练习
《三角形》复习课课堂检测
姓名: 成绩:
(1)在中,若,则的度数是( )
A. B. C. D.
(2)已知三角形两边的长分别是4和10,则此三角形第三边的长可能是( )
(
第(3)题图
) A.5 B、6 C、11 D.16
(3)如图,是斜边的中线,且,
则的长为
(
第(4)题图
)
(4)点D、E分别是△ABC边AB、AC的中点。
若DE=8,则BC= ;
(5)如图,将三角尺的直角顶点放在直尺的一边上,
∠1=30°,∠2=50°,则∠3的度数等于 ;
(
第(5)题图
)
师生活动:学生练习,老师巡堂。PPT展示答案,同学互评,大致统计100分的同学。
设计意图:对本节课复习内容进行一个简单的检测。选择题、填空题,再次体现考纲的要求。题目考点单一,也能增强学生的信心。计划用时5分钟。
(六)小结:小结一下本节课复习内容。
课后反思:
本节课中,用题目替代了知识点的讲解,所以老师讲的时间少,学生做练习的时间多,分组进行讨论,调动学生学习的积极性。本班学生的学习基础比较薄弱,所以想用的练习题比较简单,基本每题只用一个知识点就基本能解决问题,学生练习起来有成功感,而且在组长的带领下、指导下,敢于发问,组长也能积极回答,整个的课堂学习气氛是比较活跃的。本节复习课,收到了良好的复习效果。
台山市教研室黎主任的分析:
1、将知识点题目化,是本节课的亮点。这节课的概念定理很多,若逐点的讲解会用时颇多,且老师的讲述完成是无效教学,会做的学生不想听,不会的学生听不懂。将知识点题目化,学生在答题练习中回顾知识要点,有提高了答题能力。
2、课堂教学中小组的作用,能充分的调动学生的积极性,活跃了课堂,提高学生的参与度,提高了教学效率。
3、本节课的教学内容是根据学生的学情确定的,难度控制在能解答中考的简单选择题及填空题。以题目练习代替知识复述,以指导学生练习代替老师讲解,主要处理符合学生实际,能使基础较弱的学生学得进去,中考能得分。
一、教学目的
复习三角形有关的概念,等腰三角形、直角三角形的性质及判定定理;能根据给出的图形和条件准确说出相关的结论,熟练运用三角形有关定义和定理解答简单数学问题。
二、教学内容
三角形的有关定义和定理,等腰三角形、直角三角形的性质及判定定理
(
引入
学生练习
课堂检测
)三、教学流程
四、教学手段:老师精讲,以学生练习、讨论为主;PPT展示
五、教学过程
(一)引入本节课的复习内容,《三角形》考题类型。计划用时2分钟
(二)学生练习
一、三角形的边、角关系
考点内容 考点练习(A)
(1)三角形的边、角关系 ①三角形的任何两边之和大于第三边,任何两边之差小于第三边; ②三角形的内角和等于180 ,外角和等于360 ; ③三角形的一个外角等于与它不相邻的两个内角之和。 (1)已知三角形的两边长分别是4和10,则此三角形第三边的长的取值范围是 ; (2)在△ABC中,∠A=60 , ∠B=70 , 则∠C= ; (3)如图,A、C、D共线, ∠A=30 , ∠B=70 , 则∠BCD= ;
(2)三角形的主要线段 ①三角形的高: ②三角形的角平分线: ③三角形的中线: ④三角形中位线:连接三角形两边的中点的线段叫做三角形的中位线。 ⑤三角形的中位线性质:三角形的中位线平行于第三边且等于第三边的一半。 (4)如图,AD是△ABC的高, ∠B=60 ,∠BAD= ; (5)如图,BD是△ABC的角平分线,若∠1=40 ,∠ABC = 。 (6)如图,△ABC的中线AD, ①若BC=10,则BD= ; ②若BD=10,则BC= 。 (7)如图,D、E分别是AB、AC的中点,若∠B=50 ,BC=10, 则∠ADE= ,DE= 。
(3)三角形的稳定性 (8)下列各个图形中,那种图形具有稳定性( ) (A)(B)(C)(D)
(4)角平分线 ①角平分线上的点到角两边的距离相等; ②角的内部到角的两边距离相等的点在角的平分线上. (9)如图,BF平分∠ABC,FD⊥BA于点D、FE⊥BC于点E,若DF=8, 则FE= ; (10)如图,FD⊥BA于点D、FE⊥BC于点E,且FD=FE,若∠1=25 , 则∠2的度数是 ;
(5)垂直平分线 ①线段垂直平分线上的点到线段两端点的距离相等; ②到线段两端距离相等的点在线段的垂直平分线上. (11)EF是AB的垂直平分线,交AB于点D,若CA=5,则CB= ; (12)如图,EA=EB,CA=CB,若AB=10,则AD= ;
师生活动:学生练习,老师巡堂,PPT展示答案,小组内讲评消化。
设计意图:左边考点内容,右边对应练习,让学生边看考点,边做练习,以题目体现对知识点掌握的程度,达到“温故”的目的。组内讲评消化,既能加深学生对知识理解、应用,又能提高学生的表达能力,促进同学之间的感情。计划用时15分钟。
(
第(2)题图
)考点练习(B)
(1)下列长度的三条线段,能组成三角形的是( )
(A)1、2、3 (B)3、4、5
(C)2、4、8 (D)3、5、10
(2)如图所示,∠B= ;
(
第(3)题图
)(3)如图,△ABC中,AB=5,BC=6,CA=7,
D、E、F分别是三边的中点,则△DEF的周长为 ;
(4)如图,直线a∥b,∠1=75°,∠2=35°,
则∠3的度数是
(
第(4)题图
) (
第(5)题图
)
(5)如图,△ABC中,∠ABC=90 ,AD平分∠BAC,DE⊥AC于点E,若DE=6,则DB= 。
师生活动:学生练习,老师巡堂,批改几位完成较快的同学,请他去批改别的同学的答案,讲解。PPT展示答案,问同学需要讲评,根据学生的实际,挑1~2题目简单的讲评。
设计意图:经过(A)的练习,(B)是对三角形三边关系等进行一个小检测,巩固三角形三边关系等。计划用时5分钟。
(三)学生练习
二、等腰三角形
考点内容 考点练习(A)
(1)等腰三角形: 定义:有两边相等的三角形是等腰三角形; 性质: ①等边对等角; ②“三线合一”; 判定:等角对等边。 (1)如图,△ABC中,AB=AC, ∠B=46 ,则∠C= ; (2)如图,△ABC中,AB=AC, AD⊥BC于D,若BC=10, 则BD= ; (3)如图,△ABC中,∠A=36 ,∠B=72 ,则这个三角形 是 三角形;
(2)等边三角形: 定义:三边都相等的三角形是等边三角形; 性质:①三边相等; ②三角相等,都是60 ; 判定:①三边相等的三角形; ②三个内角都相等的三角形; ③有一个内角是60 的等腰三角形 (4)等边△ABC的边长为3,则△ABC的周长是 ; (5)如图,△ABC中,BC=BA, ∠A=60 ,则△ABC 是 三角形。
师生活动:学生练习,老师巡堂,PPT展示答案,小组内讲评消化。
设计意图:左边考点内容,右边对应练习,让学生边看考点,边做练习,以题目体现对知识点掌握的程度。计划用时5分钟。
考点练习(B)
(
第(3)题图
)(1)已知等腰三角形的一个内角是100 ,则此等腰三角形的另外两个内角分别是 ;
(2)一个等腰三角形的两边长分别是4和7,则它的周长为 ;
(3)如图,△ABC是等边三角形,DE∥BC,分别交AB、AC于点D、E,则△ADE是 三角形。
(
第(4)题图
)
(4)如图,△ABC中,AB=AC,D是BC的中点,
∠B=50 ,则∠BAD= , ∠BAC= 。
师生活动:学生练习,老师巡堂,批改几位完成较快的同学,请他去批改别的同学的答案,讲解。PPT展示答案,问同学需要讲评,根据学生的实际,挑1~2题目简单的讲评。
设计意图:经过(A)的练习,(B)是对等腰三角形进行一个小检测,巩固等腰三角形的性质与判定。计划用时5分钟。
(四)学生练习
三、直角三角形
考点内容 考点练习(A)
(1)直角三角形 ①直角三角形的两个锐角互余; ②直角三角形中30 角所对的直角边是斜边的一半; ③直角三角形中,斜边上的中线等于斜边的一半; ④勾股定理:直角三角形中,两直角边的平方和等于斜边的平方; ⑤勾股定理逆定理:若一个三角形中有两条边的平方和等于第三边的平方,那么这个三角形是直角三角形。 (1) Rt△ABC中,∠C=90 , ∠A=40 , 则∠B= 。 (2)如图,Rt△ABC中, ∠C=90 ,∠A=30 ,AB=10, 则BC= ; (3)如图,△ABC中, ∠ACB=90 ,D是AB的中点,AB=10, 则CD= ; (4)如图,Rt△ABC中, ∠C=90 ,AC=8,BC=6, 则AB= ; (5)以下各组数为边长,不能组成直角三角形的是( ) (A)2、3、4 (B)3、4、5 (C)10、8、6 (D)5、13、12
师生活动:学生练习,老师巡堂,PPT展示答案,小组内讲评消化。
设计意图:左边考点内容,右边对应练习,让学生边看考点,边做练习,以题目体现对知识点掌握的程度。组内讲评消化。计划用时5分钟。
(
第1、2题图
)
考点练习(B)
(1)如图,Rt△ABC的斜边AB的中线CD=1,则AB的长为 ;
(2)如图,CD是Rt△ABC斜边AB的中线,∠B=30 ,AB=10,则△ACD 的周长是 ;
(3)已知△ABC中,AB=5,BC=12,CA=13, 那么△ABC是( )
(A)锐角三角形 (B)等腰三角形 (C)等边三角形 (D)直角三角形
(4)直角三角形中,一直角边长是6,斜边是10,则另外的一直角边的长是 。
(5)Rt△ABC中,∠C=90 ,∠A=∠B ,则∠B= 。
师生活动:学生练习,老师巡堂,批改几位完成较快的同学,请他去批改别的同学的答案,讲解。PPT展示答案,问同学需要讲评,根据学生的实际,挑1~2题目简单的讲评。
设计意图:经过(A)的练习,(B)是对直角三角形进行一个小检测,巩固直角三角形的性质与判定。计划用时5分钟。
(五)学生练习
《三角形》复习课课堂检测
姓名: 成绩:
(1)在中,若,则的度数是( )
A. B. C. D.
(2)已知三角形两边的长分别是4和10,则此三角形第三边的长可能是( )
(
第(3)题图
) A.5 B、6 C、11 D.16
(3)如图,是斜边的中线,且,
则的长为
(
第(4)题图
)
(4)点D、E分别是△ABC边AB、AC的中点。
若DE=8,则BC= ;
(5)如图,将三角尺的直角顶点放在直尺的一边上,
∠1=30°,∠2=50°,则∠3的度数等于 ;
(
第(5)题图
)
师生活动:学生练习,老师巡堂。PPT展示答案,同学互评,大致统计100分的同学。
设计意图:对本节课复习内容进行一个简单的检测。选择题、填空题,再次体现考纲的要求。题目考点单一,也能增强学生的信心。计划用时5分钟。
(六)小结:小结一下本节课复习内容。
课后反思:
本节课中,用题目替代了知识点的讲解,所以老师讲的时间少,学生做练习的时间多,分组进行讨论,调动学生学习的积极性。本班学生的学习基础比较薄弱,所以想用的练习题比较简单,基本每题只用一个知识点就基本能解决问题,学生练习起来有成功感,而且在组长的带领下、指导下,敢于发问,组长也能积极回答,整个的课堂学习气氛是比较活跃的。本节复习课,收到了良好的复习效果。
台山市教研室黎主任的分析:
1、将知识点题目化,是本节课的亮点。这节课的概念定理很多,若逐点的讲解会用时颇多,且老师的讲述完成是无效教学,会做的学生不想听,不会的学生听不懂。将知识点题目化,学生在答题练习中回顾知识要点,有提高了答题能力。
2、课堂教学中小组的作用,能充分的调动学生的积极性,活跃了课堂,提高学生的参与度,提高了教学效率。
3、本节课的教学内容是根据学生的学情确定的,难度控制在能解答中考的简单选择题及填空题。以题目练习代替知识复述,以指导学生练习代替老师讲解,主要处理符合学生实际,能使基础较弱的学生学得进去,中考能得分。
