4.4.2对数函数的图象和性质(第二课时)(共27张PPT)
文档属性
| 名称 | 4.4.2对数函数的图象和性质(第二课时)(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-12 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
第4章 指数函数与对数函数
4.4 对数函数
4.4.2 对数函数的图象和性质(第二课时)
人教A版(2019)
教学目标
学习目标 数学素养
1.进一步理解对数函数的图像和性质. 1.数形结合素养.
2.能利用对数函数性质来解决应用问题. 2.逻辑推理、化归转化素养
温故知新
01
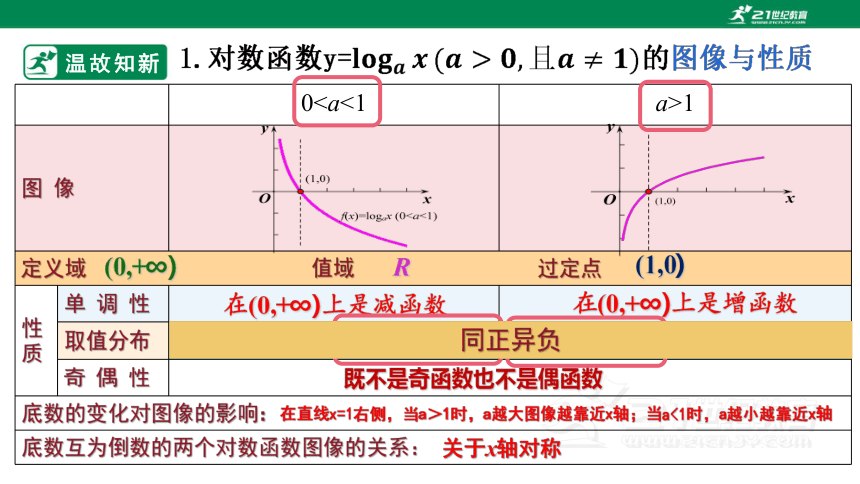
图 像
定义域 值域 过定点 性质 单 调 性
取值分布
奇 偶 性 底数的变化对图像的影响: 底数互为倒数的两个对数函数图像的关系: (0,+∞)
R
(1,0)
在(0,+∞)上是增函数
既不是奇函数也不是偶函数
当x>1时y>0;当0当x>1时y<0;当00.
在(0,+∞)上是减函数
在直线x=1右侧,当a>1时,a越大图像越靠近x轴;当a<1时,a越小越靠近x轴
关于x轴对称
同正异负
1.对数函数y=的图像与性质
温故知新
2. 反函数
根据运算性质可以由一个推导出另外一个,并且一个函数的定义域和值域分别是另外一个函数的值域和定义域的,我们就称它们互为反函数(inverse function).
一般地,指数函数与对数函数互为反函数,它们的定义域与值域正好互换.
互为反函数的两个函数:①它们的定义域与值域正好互换;②它们的图象关于直线y=x对称.
新知传授
题型1.反函数
【例1】⑴函数f(x)= 的反函数是 .
⑵函数y=3x-2的反函数是 .
⑶若函数y=f(x)是函数(a>0,且a≠1)的反函数,其图象经过点,则a=________.
解:
⑴由同底数的指数函数与对数函数互为反函数,得
f(x)= 的反函数是
⑵∵y=3x-2
交换x与y,得原函数的反函数为.
⑶∵函数y=f(x)图象经过点.
∴函数y=的图象经过点.
∴.
则.
新知传授
题型1.反函数
求反函数的步骤:
(1)反解出x ;
(2)交换x,y的位置;
(3)求出原函数的值域,作为反函数的定义域.
初试身手
题型1.反函数
1.求出下列函数的反函数:
⑴函数的反函数是 ;
⑵函数的反函数是 ;
⑶函数的反函数是 .
新知讲解
【例2】⑴函数f(x)=ln(1+x)的定义域为 ;
⑵函数的定义域为 ;
⑶函数的定义域为 .
解:
⑴要使函数f(x)=ln(1+x)有意义,必有x+1>0,即x>-1
则函数f(x)=ln(x+1)的定义域为(-1,+∞).
题型2.求对数型复合函数的定义域
(-1,+∞)
⑵要使函数有意义,必有,
解得1则函数的定义域为(1,2].
⑶要使函数有意义,必有,即,
解得0则函数的定义域为(0,2].
(1,2]
(0,2]
新知讲解
求对数函数定义域的注意事项
求与对数函数有关的函数定义域时,除遵循前面已学习过的求函数定义域的方法外,还要对这种函数自身作如下要求:一是要特别注意真数大于零;二是要注意对数的底数大于零且不等于1;三是按底数的取值应用单调性解不等式.
题型2.求对数型复合函数的定义域
新知讲解
⑴关于对数型函数的单调性由两点决定.一是底数a>1还是0题型3.与对数函数复合的函数的单调性
函数 单调性 外层函数 增函数 增函数 减函数 减函数
内层函数 增函数 减函数 增函数 减函数
复合函数
增函数
减函数
减函数
增函数
同增异减
例如:y=ln(1+x)的内层函数 ,外层函数 .
再如:的内层函数 ,
外层函数 .
新知讲解
【例3】求函数单调区间.
解:
题型3.对数型复合函数的单调性
分析:函数先要满足,确定函数f(x)的定义域,再考虑外函数单调性 ,然后确定内函数的单调区间.
又∵在(-∞,-1)上单调递减,在(3,+∞)上单调递增.
∴函数f(x)的定义域为(-∞,-1)∪(3,+∞).
∵,解得x>3或x<-1,
而函数y=在(0,+∞)上单调递增.
∴函数f(x)的单调递减区间为(-∞,-1),单调递增区间为(3,+∞).
新知讲解
题型3.对数型复合函数的单调性
求复合函数单调性的具体步骤:
①求定义域;
②拆分函数;
③分别求出y=f(u),u=g(x)的单调性;
④按“同增异减”得出复合函数的单调性.
初试身手
2.求解下列单调性问题:
⑴函数f(x)=ln(1+x)在区间(-1,+∞)上单调 ;
⑵函数f(x)=的单调递增区间为( )
A.(1,2) B.(2,+∞) C.(0,1) D.(-∞,0)
解:
(1)函数f(x)=ln(1+x)的定义域为(-1,+∞)
令u=1+x,则f(x)=lnu,而底数e>1,y=lnu为增函数,u=1+x单调递增.
则函数f(x)在(-1,+∞)上单调递增.
递增
⑵∵,解得0∴函数f(x)的定义域为(0,2).
又∵在(0,1)上单调递增,在(1,2)上单调递减.
令,则f(x)=,而,f(x)=为减函数.
∴函数f(x)单调递增区间为(1,2),故选A.
A
新知讲解
【例4】求下列函数的值域:
(1) ; (2) .
解:
题型4.求对数型复合函数的值域
(1)方法1:函数f(x)=的定义域为R.
∵,
∴,
∴的值域为{y|y≥2}.
方法2:函数f(x)=的定义域为R.
令u=,函数u=在(-∞,0)上递减,在(0,+∞)上递增,且
函数f(x)=
∴在在(-∞,0)上递减,在(0,+∞)上递增.
则当x=0时,函数f(x)取最小值2,而且f(x)无最大值.
∴的值域为{y|y≥2}.
新知讲解
【例4】求下列函数的值域:
(1) ; (2) .
解:
题型4.求对数型复合函数的值域
⑵∵,解得-1又∵函数在(0,+∞)单调递减,
∵,
∴,
∴.
∴的值域为{y|y≥-2}.
设,则.
新知讲解
题型4.求对数型复合函数的值域
对数型复合函数的值域的求解方法与步骤
对于形如的复合函数,其值域的求解步骤如下:
第1步:分解成两个函数;
第2步:求的定义城;
第3步:求u的取值范围
第4步:利用的单调性求出的范围.
初试身手
3.⑴函数的值域为 .
⑵函数在上的最大值为( )
A.0 B.1 C.2 D.a
解:
题型4.求对数型复合函数的值域
⑴∵,且f(x)在(-∞,+∞)上单调递增.
∴,
则该函数的值域为(0,+∞).
(0,+∞)
⑵∵,∴在上单调递减.
∴,故选C.
C
新知讲解
【例5】解下列不等式:
⑴; ⑵.
解:
(1)原不等式可化为,又∵3>1,
∴原不等等价于,解得1则原不等式的解集为{x|1(2)∵,
题型5.求解对数不等式
∴原不等等价于,解得,
则原不等式的解集为.
新知讲解
题型5.求解对数不等式
对数不等式解法:
对于形如的求解步骤如下:
第1步:根据a>1还是0第2步:a>1,原不等式等价于;0;
第3步:解不等式组;
第4步:得到原不等式解集.
初试身手
4.解关于x的不等式.
解:
①当a>1时,原不等式等价于,解得,
则原不等式的解集为.
②当0题型5.求解对数不等式
则原不等式的解集为.
新知讲解
【例6】已知函数
⑴求函数的定义域;
⑵判定的奇偶性.
解:
(1)要使函数有意义,必有,解得 x<-1或x>1,
则函数的定义域为(-∞,-1)∪(1,+∞).
(2)∵函数的定义域(-∞,-1)∪(1,+∞)关于原点对称,
题型6.对数函数型复合函数的奇偶性
∴对 x∈(-∞,-1)∪(1,+∞),-x∈(-∞,-1)∪(1,+∞).
则函数.
.
新知讲解
题型6.对数函数型复合函数的奇偶性
拓展:1.函数的定义域为 ,奇偶性为 .
2.函数的定义域为 ,奇偶性为 .
总结:形如,,,(a>0且a≠1,b>0)等函数均为 .
奇函数
奇函数
(-∞,-b)∪(b,+∞)
(-b,b)
奇函数
初试身手
5.设函数,则是( ).
A.奇函数,且在(0,1)上是增函数 B.奇函数,且在(0,1)上是减函数
C.偶函数,且在(0,1)上是增函数 D.偶函数,且在(0,1)上是减函数
解:
要使函数有意义,必有,解得 -1则函数的定义域为(-1,1).
题型6.对数函数型复合函数的奇偶性
∵对 x∈(-1,1),-x∈(-1,1),
则函数.
.
显然在(-1,1)上单调递增,则在(0,1)上也是增函数.故选A.
A
作业布置
作业:
1.若函数在(0,+∞)上是增函数,则实数a的取值范围是 .
2.函数单调递减区间为 .
3.已知a为常数,函数.若的反函数的图象经过点(3,1),则
a= .
4.求函数的值域.
5.若函数为偶函数,则a= .
6.不等式的解集为 .
7.已知函数,,则 .
8.已知函数.
⑴求函数的定义域和值域;
⑵若有最小值为-2,求a的值.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第4章 指数函数与对数函数
4.4 对数函数
4.4.2 对数函数的图象和性质(第二课时)
人教A版(2019)
教学目标
学习目标 数学素养
1.进一步理解对数函数的图像和性质. 1.数形结合素养.
2.能利用对数函数性质来解决应用问题. 2.逻辑推理、化归转化素养
温故知新
0
图 像
定义域 值域 过定点 性质 单 调 性
取值分布
奇 偶 性 底数的变化对图像的影响: 底数互为倒数的两个对数函数图像的关系: (0,+∞)
R
(1,0)
在(0,+∞)上是增函数
既不是奇函数也不是偶函数
当x>1时y>0;当0
在(0,+∞)上是减函数
在直线x=1右侧,当a>1时,a越大图像越靠近x轴;当a<1时,a越小越靠近x轴
关于x轴对称
同正异负
1.对数函数y=的图像与性质
温故知新
2. 反函数
根据运算性质可以由一个推导出另外一个,并且一个函数的定义域和值域分别是另外一个函数的值域和定义域的,我们就称它们互为反函数(inverse function).
一般地,指数函数与对数函数互为反函数,它们的定义域与值域正好互换.
互为反函数的两个函数:①它们的定义域与值域正好互换;②它们的图象关于直线y=x对称.
新知传授
题型1.反函数
【例1】⑴函数f(x)= 的反函数是 .
⑵函数y=3x-2的反函数是 .
⑶若函数y=f(x)是函数(a>0,且a≠1)的反函数,其图象经过点,则a=________.
解:
⑴由同底数的指数函数与对数函数互为反函数,得
f(x)= 的反函数是
⑵∵y=3x-2
交换x与y,得原函数的反函数为.
⑶∵函数y=f(x)图象经过点.
∴函数y=的图象经过点.
∴.
则.
新知传授
题型1.反函数
求反函数的步骤:
(1)反解出x ;
(2)交换x,y的位置;
(3)求出原函数的值域,作为反函数的定义域.
初试身手
题型1.反函数
1.求出下列函数的反函数:
⑴函数的反函数是 ;
⑵函数的反函数是 ;
⑶函数的反函数是 .
新知讲解
【例2】⑴函数f(x)=ln(1+x)的定义域为 ;
⑵函数的定义域为 ;
⑶函数的定义域为 .
解:
⑴要使函数f(x)=ln(1+x)有意义,必有x+1>0,即x>-1
则函数f(x)=ln(x+1)的定义域为(-1,+∞).
题型2.求对数型复合函数的定义域
(-1,+∞)
⑵要使函数有意义,必有,
解得1
⑶要使函数有意义,必有,即,
解得0
(1,2]
(0,2]
新知讲解
求对数函数定义域的注意事项
求与对数函数有关的函数定义域时,除遵循前面已学习过的求函数定义域的方法外,还要对这种函数自身作如下要求:一是要特别注意真数大于零;二是要注意对数的底数大于零且不等于1;三是按底数的取值应用单调性解不等式.
题型2.求对数型复合函数的定义域
新知讲解
⑴关于对数型函数的单调性由两点决定.一是底数a>1还是0
函数 单调性 外层函数 增函数 增函数 减函数 减函数
内层函数 增函数 减函数 增函数 减函数
复合函数
增函数
减函数
减函数
增函数
同增异减
例如:y=ln(1+x)的内层函数 ,外层函数 .
再如:的内层函数 ,
外层函数 .
新知讲解
【例3】求函数单调区间.
解:
题型3.对数型复合函数的单调性
分析:函数先要满足,确定函数f(x)的定义域,再考虑外函数单调性 ,然后确定内函数的单调区间.
又∵在(-∞,-1)上单调递减,在(3,+∞)上单调递增.
∴函数f(x)的定义域为(-∞,-1)∪(3,+∞).
∵,解得x>3或x<-1,
而函数y=在(0,+∞)上单调递增.
∴函数f(x)的单调递减区间为(-∞,-1),单调递增区间为(3,+∞).
新知讲解
题型3.对数型复合函数的单调性
求复合函数单调性的具体步骤:
①求定义域;
②拆分函数;
③分别求出y=f(u),u=g(x)的单调性;
④按“同增异减”得出复合函数的单调性.
初试身手
2.求解下列单调性问题:
⑴函数f(x)=ln(1+x)在区间(-1,+∞)上单调 ;
⑵函数f(x)=的单调递增区间为( )
A.(1,2) B.(2,+∞) C.(0,1) D.(-∞,0)
解:
(1)函数f(x)=ln(1+x)的定义域为(-1,+∞)
令u=1+x,则f(x)=lnu,而底数e>1,y=lnu为增函数,u=1+x单调递增.
则函数f(x)在(-1,+∞)上单调递增.
递增
⑵∵,解得0
又∵在(0,1)上单调递增,在(1,2)上单调递减.
令,则f(x)=,而,f(x)=为减函数.
∴函数f(x)单调递增区间为(1,2),故选A.
A
新知讲解
【例4】求下列函数的值域:
(1) ; (2) .
解:
题型4.求对数型复合函数的值域
(1)方法1:函数f(x)=的定义域为R.
∵,
∴,
∴的值域为{y|y≥2}.
方法2:函数f(x)=的定义域为R.
令u=,函数u=在(-∞,0)上递减,在(0,+∞)上递增,且
函数f(x)=
∴在在(-∞,0)上递减,在(0,+∞)上递增.
则当x=0时,函数f(x)取最小值2,而且f(x)无最大值.
∴的值域为{y|y≥2}.
新知讲解
【例4】求下列函数的值域:
(1) ; (2) .
解:
题型4.求对数型复合函数的值域
⑵∵,解得-1
∵,
∴,
∴.
∴的值域为{y|y≥-2}.
设,则.
新知讲解
题型4.求对数型复合函数的值域
对数型复合函数的值域的求解方法与步骤
对于形如的复合函数,其值域的求解步骤如下:
第1步:分解成两个函数;
第2步:求的定义城;
第3步:求u的取值范围
第4步:利用的单调性求出的范围.
初试身手
3.⑴函数的值域为 .
⑵函数在上的最大值为( )
A.0 B.1 C.2 D.a
解:
题型4.求对数型复合函数的值域
⑴∵,且f(x)在(-∞,+∞)上单调递增.
∴,
则该函数的值域为(0,+∞).
(0,+∞)
⑵∵,∴在上单调递减.
∴,故选C.
C
新知讲解
【例5】解下列不等式:
⑴; ⑵.
解:
(1)原不等式可化为,又∵3>1,
∴原不等等价于,解得1
题型5.求解对数不等式
∴原不等等价于,解得,
则原不等式的解集为.
新知讲解
题型5.求解对数不等式
对数不等式解法:
对于形如的求解步骤如下:
第1步:根据a>1还是0
第3步:解不等式组;
第4步:得到原不等式解集.
初试身手
4.解关于x的不等式.
解:
①当a>1时,原不等式等价于,解得,
则原不等式的解集为.
②当0
则原不等式的解集为.
新知讲解
【例6】已知函数
⑴求函数的定义域;
⑵判定的奇偶性.
解:
(1)要使函数有意义,必有,解得 x<-1或x>1,
则函数的定义域为(-∞,-1)∪(1,+∞).
(2)∵函数的定义域(-∞,-1)∪(1,+∞)关于原点对称,
题型6.对数函数型复合函数的奇偶性
∴对 x∈(-∞,-1)∪(1,+∞),-x∈(-∞,-1)∪(1,+∞).
则函数.
.
新知讲解
题型6.对数函数型复合函数的奇偶性
拓展:1.函数的定义域为 ,奇偶性为 .
2.函数的定义域为 ,奇偶性为 .
总结:形如,,,(a>0且a≠1,b>0)等函数均为 .
奇函数
奇函数
(-∞,-b)∪(b,+∞)
(-b,b)
奇函数
初试身手
5.设函数,则是( ).
A.奇函数,且在(0,1)上是增函数 B.奇函数,且在(0,1)上是减函数
C.偶函数,且在(0,1)上是增函数 D.偶函数,且在(0,1)上是减函数
解:
要使函数有意义,必有,解得 -1
题型6.对数函数型复合函数的奇偶性
∵对 x∈(-1,1),-x∈(-1,1),
则函数.
.
显然在(-1,1)上单调递增,则在(0,1)上也是增函数.故选A.
A
作业布置
作业:
1.若函数在(0,+∞)上是增函数,则实数a的取值范围是 .
2.函数单调递减区间为 .
3.已知a为常数,函数.若的反函数的图象经过点(3,1),则
a= .
4.求函数的值域.
5.若函数为偶函数,则a= .
6.不等式的解集为 .
7.已知函数,,则 .
8.已知函数.
⑴求函数的定义域和值域;
⑵若有最小值为-2,求a的值.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
