2024鲁科版高中物理选择性必修第二册同步练习--专题强化练3 磁场中的临界、极值问题
文档属性
| 名称 | 2024鲁科版高中物理选择性必修第二册同步练习--专题强化练3 磁场中的临界、极值问题 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-11-10 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024鲁科版高中物理选择性必修第二册同步
专题强化练3 磁场中的临界、极值问题
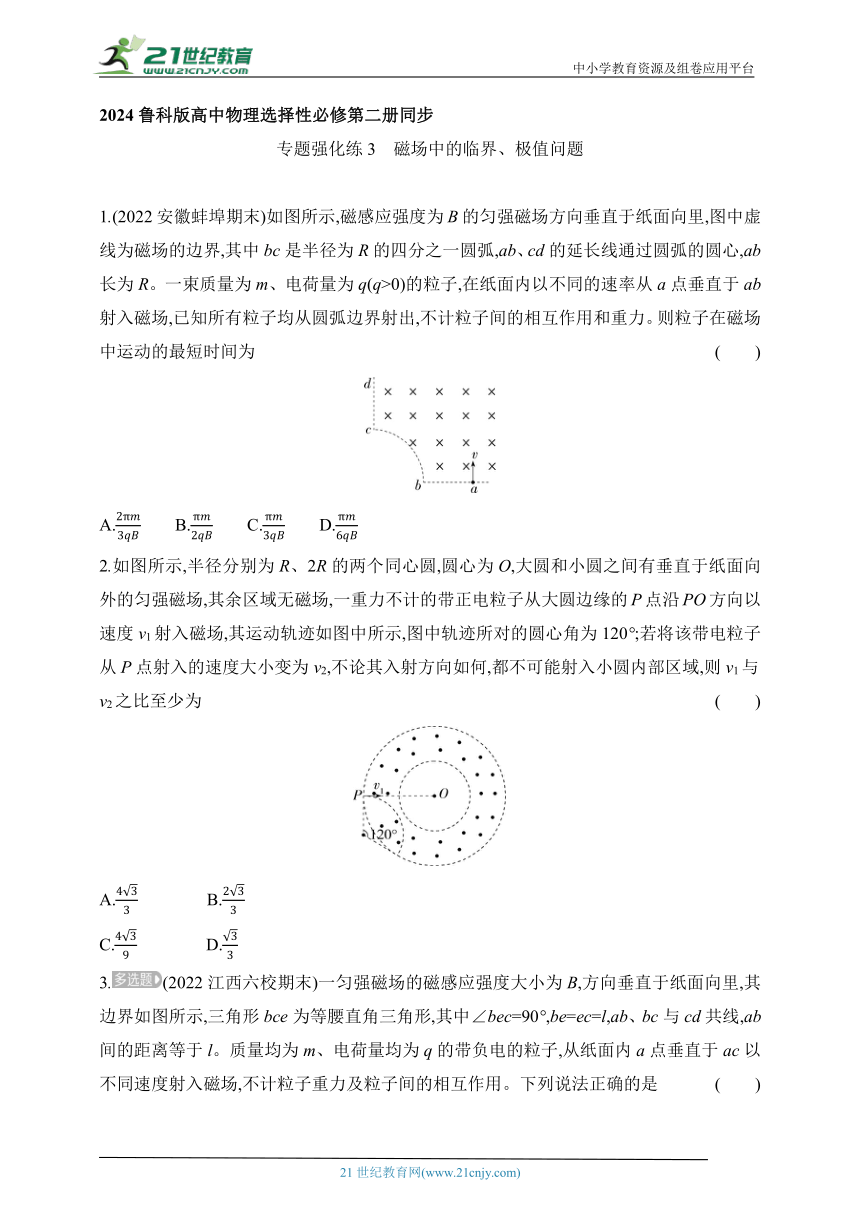
1.(2022安徽蚌埠期末)如图所示,磁感应强度为B的匀强磁场方向垂直于纸面向里,图中虚线为磁场的边界,其中bc是半径为R的四分之一圆弧,ab、cd的延长线通过圆弧的圆心,ab长为R。一束质量为m、电荷量为q(q>0)的粒子,在纸面内以不同的速率从a点垂直于ab射入磁场,已知所有粒子均从圆弧边界射出,不计粒子间的相互作用和重力。则粒子在磁场中运动的最短时间为 ( )
A. B. C. D.
2.如图所示,半径分别为R、2R的两个同心圆,圆心为O,大圆和小圆之间有垂直于纸面向外的匀强磁场,其余区域无磁场,一重力不计的带正电粒子从大圆边缘的P点沿PO方向以速度v1射入磁场,其运动轨迹如图中所示,图中轨迹所对的圆心角为120°;若将该带电粒子从P点射入的速度大小变为v2,不论其入射方向如何,都不可能射入小圆内部区域,则v1与v2之比至少为 ( )
A. B.
C. D.
3.(2022江西六校期末)一匀强磁场的磁感应强度大小为B,方向垂直于纸面向里,其边界如图所示,三角形bce为等腰直角三角形,其中∠bec=90°,be=ec=l,ab、bc与cd共线,ab间的距离等于l。质量均为m、电荷量均为q的带负电的粒子,从纸面内a点垂直于ac以不同速度射入磁场,不计粒子重力及粒子间的相互作用。下列说法正确的是 ( )
A.可以经过三角形边界的粒子的速率最小值为
B.可以经过三角形边界的粒子的速率最大值为
C.在磁场中运动时间最短的粒子速率为
D.在磁场中运动时间最短的粒子运动时间为
4.(2022山东青岛二中期中)如图所示,边界OA与OC之间分布有垂直纸面向里的匀强磁场,边界OA上有一粒子源S。某一时刻,从S平行于纸面向各个方向发射出大量带正电的同种粒子(不计粒子的重力及粒子间的相互作用),所有粒子的初速度大小相同,经过一段时间有大量粒子从边界OC射出磁场。已知∠AOC=60°,从边界OC射出的粒子在磁场中运动的最短时间等于(T为粒子在磁场中运动的周期),则从边界OC射出的粒子在磁场中运动的最长时间为 ( )
A. B. C. D.
5.(2022黑龙江哈尔滨师范大学青冈实验中学期中,改编)如图所示,在矩形区域abcd内存在磁感应强度为B、方向垂直于纸面向里的匀强磁场,矩形区域的宽ab=L,长ad=3L。一粒子源处于ad边中点O,在t=0时刻粒子源垂直于磁场发射出大量的同种带电粒子,所有粒子的初速度大小相同,方向与Od的夹角分布在0~180°范围内。已知最早到达bc边的粒子的运动时间为t=t0,粒子在磁场中做圆周运动的半径R=L,不计粒子的重力和粒子间的相互作用,求
(1)粒子在磁场中做匀速圆周运动的周期T;
(2)粒子的比荷;
(3)粒子在磁场中运动的最长时间。
6.(2021山东威海期末)如图所示,在区域Ⅰ(0≤x≤d)和区域Ⅱ(d0)的粒子从O点沿x轴正方向进入磁场,粒子离开区域Ⅰ时的速度方向与x轴正方向的夹角为30°,不计重力,求:
(1)粒子进入区域Ⅰ时的速度大小;
(2)粒子在区域Ⅱ中的运动时间;
(3)若区域Ⅱ内磁感应强度大小可变,要保证粒子能够从区域Ⅱ右侧射出,求磁感应强度大小B'应满足的条件。
专题强化练3 磁场中的临界、极值问题
1.A 2.A 3.BC 4.B
1.A 依题意,由几何知识判断可知,当粒子在磁场中做匀速圆周运动的圆心恰好在b点时,粒子在磁场中运动的圆弧所对的圆心角最小,此时粒子运动的半径r=R,由几何关系可求得此时圆弧所对应的圆心角θ=120°,所以,粒子在磁场中运动的最短时间为tmin=·=,故选A。
2.A 粒子在磁场中做圆周运动,如图,由几何知识得r1==,由洛伦兹力提供向心力,根据牛顿第二定律得qv1B=m,解得v1=,若粒子以速度大小为v2朝各个方向入射,当粒子竖直向上射入磁场时,如果粒子不能进入小圆区域,则所有粒子都不可能进入小圆区域,粒子竖直向上射入磁场且恰好不能进入小圆区域时粒子轨道半径r2=,由洛伦兹力提供向心力,根据牛顿第二定律得qv2B=m,解得v2=,则v1=v2,选项A正确,B、C、D错误。
3.BC 设粒子在磁场中运动的半径为r、速率为v,根据牛顿第二定律有qvB=m,解得r=。可以经过三角形边界的粒子的最小半径为rmin==,所以可以经过三角形边界的粒子的速率最小值为vmin==;可以经过三角形边界的粒子的最大半径为rmax==,所以可以经过三角形边界的粒子的速率最大值为vmax==,故A错误,B正确。根据几何关系可知,打在b、c两点所在直线的粒子,运动圆弧所对的圆心角最大,运动时间最长,为半个周期,而打在be边上的粒子的运动时间随到b点的距离增大而减小,打在ec边上的粒子的运动时间随到e点的距离增大而增大,因此打在e点的粒子运动时间最短,此时粒子的运动半径为l,所以速率为v=,其运动时间为t=T=·=,故C正确,D错误。
4.B 粒子在磁场中沿逆时针方向做匀速圆周运动,由于所有粒子的速度大小都相同,故弧长越小,粒子在磁场中运动时间就越短。由S作OC的垂线交OC于D,可知粒子轨迹过D点时在磁场中运动时间最短,根据最短时间为,结合几何知识可得粒子做圆周运动的轨迹半径等于SD(如图);由于粒子沿逆时针方向运动,故沿SA方向射出的粒子在磁场中运动的时间最长,根据几何知识易知SE=2SD,则此粒子在磁场中运动轨迹恰为半圆,故粒子在磁场中运动的最长时间为,选项B正确,A、C、D错误。
5.答案 (1)6t0 (2) (3)2t0
解析 (1)最早到达bc边的粒子在磁场中运动的轨迹如图甲,其对应圆心角为θ,由几何关系有sin =,所以θ=60°
=,解得T=6t0
(2)粒子做圆周运动的向心力由洛伦兹力提供,根据牛顿第二定律得qvB=m,又有v=
所以T==6t0
解得=
(3)如图乙所示,在磁场中运动时间最长的粒子的轨迹与bc边相切于N点,与ab边的交点为M点,圆轨迹的半径为O2O=O2M=L,O2a=,由几何关系知轨迹对应的圆心角φ为120°,粒子在磁场中运动的最长时间tmax==2t0。
方法技巧 解题关键是画出粒子的运动轨迹,根据几何知识确定隐含的极值条件和粒子运动轨迹对应的圆心角。
6.答案 (1) (2) (3)B'<3B
解析 (1)根据题意画出粒子的运动轨迹如图所示
设粒子在区域Ⅰ内运动的轨迹半径为r1,根据几何知识得d2+(r1 cos 30°)2=
根据牛顿第二定律得qvB=m
联立解得v=
(2)设粒子在区域Ⅱ内运动的轨迹半径为r2,周期为T,则根据牛顿第二定律得2Bqv=m,解得r2=d
根据几何知识得,粒子在区域Ⅱ中运动的轨迹所对应的圆心角θ=,据运动学公式得v=
粒子在区域Ⅱ中运动的时间t=T
联立各式解得t=
(3)粒子运动轨迹刚好与区域Ⅱ右侧相切时,轨迹如图所示
设粒子刚好从区域Ⅱ右侧射出时,运动的轨迹半径为r3,根据几何知识得r3+r3 sin 30°=d
根据牛顿第二定律得B'qv=m
联立各式解得B'=3B
所以,要保证粒子能从区域Ⅱ右侧射出,磁感应强度应满足的条件为B'<3B
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024鲁科版高中物理选择性必修第二册同步
专题强化练3 磁场中的临界、极值问题
1.(2022安徽蚌埠期末)如图所示,磁感应强度为B的匀强磁场方向垂直于纸面向里,图中虚线为磁场的边界,其中bc是半径为R的四分之一圆弧,ab、cd的延长线通过圆弧的圆心,ab长为R。一束质量为m、电荷量为q(q>0)的粒子,在纸面内以不同的速率从a点垂直于ab射入磁场,已知所有粒子均从圆弧边界射出,不计粒子间的相互作用和重力。则粒子在磁场中运动的最短时间为 ( )
A. B. C. D.
2.如图所示,半径分别为R、2R的两个同心圆,圆心为O,大圆和小圆之间有垂直于纸面向外的匀强磁场,其余区域无磁场,一重力不计的带正电粒子从大圆边缘的P点沿PO方向以速度v1射入磁场,其运动轨迹如图中所示,图中轨迹所对的圆心角为120°;若将该带电粒子从P点射入的速度大小变为v2,不论其入射方向如何,都不可能射入小圆内部区域,则v1与v2之比至少为 ( )
A. B.
C. D.
3.(2022江西六校期末)一匀强磁场的磁感应强度大小为B,方向垂直于纸面向里,其边界如图所示,三角形bce为等腰直角三角形,其中∠bec=90°,be=ec=l,ab、bc与cd共线,ab间的距离等于l。质量均为m、电荷量均为q的带负电的粒子,从纸面内a点垂直于ac以不同速度射入磁场,不计粒子重力及粒子间的相互作用。下列说法正确的是 ( )
A.可以经过三角形边界的粒子的速率最小值为
B.可以经过三角形边界的粒子的速率最大值为
C.在磁场中运动时间最短的粒子速率为
D.在磁场中运动时间最短的粒子运动时间为
4.(2022山东青岛二中期中)如图所示,边界OA与OC之间分布有垂直纸面向里的匀强磁场,边界OA上有一粒子源S。某一时刻,从S平行于纸面向各个方向发射出大量带正电的同种粒子(不计粒子的重力及粒子间的相互作用),所有粒子的初速度大小相同,经过一段时间有大量粒子从边界OC射出磁场。已知∠AOC=60°,从边界OC射出的粒子在磁场中运动的最短时间等于(T为粒子在磁场中运动的周期),则从边界OC射出的粒子在磁场中运动的最长时间为 ( )
A. B. C. D.
5.(2022黑龙江哈尔滨师范大学青冈实验中学期中,改编)如图所示,在矩形区域abcd内存在磁感应强度为B、方向垂直于纸面向里的匀强磁场,矩形区域的宽ab=L,长ad=3L。一粒子源处于ad边中点O,在t=0时刻粒子源垂直于磁场发射出大量的同种带电粒子,所有粒子的初速度大小相同,方向与Od的夹角分布在0~180°范围内。已知最早到达bc边的粒子的运动时间为t=t0,粒子在磁场中做圆周运动的半径R=L,不计粒子的重力和粒子间的相互作用,求
(1)粒子在磁场中做匀速圆周运动的周期T;
(2)粒子的比荷;
(3)粒子在磁场中运动的最长时间。
6.(2021山东威海期末)如图所示,在区域Ⅰ(0≤x≤d)和区域Ⅱ(d
(1)粒子进入区域Ⅰ时的速度大小;
(2)粒子在区域Ⅱ中的运动时间;
(3)若区域Ⅱ内磁感应强度大小可变,要保证粒子能够从区域Ⅱ右侧射出,求磁感应强度大小B'应满足的条件。
专题强化练3 磁场中的临界、极值问题
1.A 2.A 3.BC 4.B
1.A 依题意,由几何知识判断可知,当粒子在磁场中做匀速圆周运动的圆心恰好在b点时,粒子在磁场中运动的圆弧所对的圆心角最小,此时粒子运动的半径r=R,由几何关系可求得此时圆弧所对应的圆心角θ=120°,所以,粒子在磁场中运动的最短时间为tmin=·=,故选A。
2.A 粒子在磁场中做圆周运动,如图,由几何知识得r1==,由洛伦兹力提供向心力,根据牛顿第二定律得qv1B=m,解得v1=,若粒子以速度大小为v2朝各个方向入射,当粒子竖直向上射入磁场时,如果粒子不能进入小圆区域,则所有粒子都不可能进入小圆区域,粒子竖直向上射入磁场且恰好不能进入小圆区域时粒子轨道半径r2=,由洛伦兹力提供向心力,根据牛顿第二定律得qv2B=m,解得v2=,则v1=v2,选项A正确,B、C、D错误。
3.BC 设粒子在磁场中运动的半径为r、速率为v,根据牛顿第二定律有qvB=m,解得r=。可以经过三角形边界的粒子的最小半径为rmin==,所以可以经过三角形边界的粒子的速率最小值为vmin==;可以经过三角形边界的粒子的最大半径为rmax==,所以可以经过三角形边界的粒子的速率最大值为vmax==,故A错误,B正确。根据几何关系可知,打在b、c两点所在直线的粒子,运动圆弧所对的圆心角最大,运动时间最长,为半个周期,而打在be边上的粒子的运动时间随到b点的距离增大而减小,打在ec边上的粒子的运动时间随到e点的距离增大而增大,因此打在e点的粒子运动时间最短,此时粒子的运动半径为l,所以速率为v=,其运动时间为t=T=·=,故C正确,D错误。
4.B 粒子在磁场中沿逆时针方向做匀速圆周运动,由于所有粒子的速度大小都相同,故弧长越小,粒子在磁场中运动时间就越短。由S作OC的垂线交OC于D,可知粒子轨迹过D点时在磁场中运动时间最短,根据最短时间为,结合几何知识可得粒子做圆周运动的轨迹半径等于SD(如图);由于粒子沿逆时针方向运动,故沿SA方向射出的粒子在磁场中运动的时间最长,根据几何知识易知SE=2SD,则此粒子在磁场中运动轨迹恰为半圆,故粒子在磁场中运动的最长时间为,选项B正确,A、C、D错误。
5.答案 (1)6t0 (2) (3)2t0
解析 (1)最早到达bc边的粒子在磁场中运动的轨迹如图甲,其对应圆心角为θ,由几何关系有sin =,所以θ=60°
=,解得T=6t0
(2)粒子做圆周运动的向心力由洛伦兹力提供,根据牛顿第二定律得qvB=m,又有v=
所以T==6t0
解得=
(3)如图乙所示,在磁场中运动时间最长的粒子的轨迹与bc边相切于N点,与ab边的交点为M点,圆轨迹的半径为O2O=O2M=L,O2a=,由几何关系知轨迹对应的圆心角φ为120°,粒子在磁场中运动的最长时间tmax==2t0。
方法技巧 解题关键是画出粒子的运动轨迹,根据几何知识确定隐含的极值条件和粒子运动轨迹对应的圆心角。
6.答案 (1) (2) (3)B'<3B
解析 (1)根据题意画出粒子的运动轨迹如图所示
设粒子在区域Ⅰ内运动的轨迹半径为r1,根据几何知识得d2+(r1 cos 30°)2=
根据牛顿第二定律得qvB=m
联立解得v=
(2)设粒子在区域Ⅱ内运动的轨迹半径为r2,周期为T,则根据牛顿第二定律得2Bqv=m,解得r2=d
根据几何知识得,粒子在区域Ⅱ中运动的轨迹所对应的圆心角θ=,据运动学公式得v=
粒子在区域Ⅱ中运动的时间t=T
联立各式解得t=
(3)粒子运动轨迹刚好与区域Ⅱ右侧相切时,轨迹如图所示
设粒子刚好从区域Ⅱ右侧射出时,运动的轨迹半径为r3,根据几何知识得r3+r3 sin 30°=d
根据牛顿第二定律得B'qv=m
联立各式解得B'=3B
所以,要保证粒子能从区域Ⅱ右侧射出,磁感应强度应满足的条件为B'<3B
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
