2024鲁科版高中物理选择性必修第三册同步练习--第5节 气体实验定律
文档属性
| 名称 | 2024鲁科版高中物理选择性必修第三册同步练习--第5节 气体实验定律 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-11-10 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024鲁科版高中物理选择性必修第三册同步
第5节 气体实验定律
基础过关练
题组一 玻意耳定律
1.各种卡通形状的氢气球受到孩子们的喜欢,若孩子一不小心松手,氢气球会飞向天空,上升到一定高度会胀破,关于其胀破的原因,下列说法中正确的是 ( )
A.球内氢气温度升高
B.球内氢气压强增大
C.球内气体体积增大
D.球内外的压力差超过球的承受限度
2.如图所示为一定质量的气体在不同温度下的两条等温线,则下列说法中正确的是( )
A.一定质量的气体在发生等温变化时,其压强与体积成反比
B.一定质量的气体,在不同温度下的等温线是不同的
C.T1>T2
D.T13.有一导热气缸,气缸内用质量为m的活塞密封一定质量的理想气体,活塞的横截面积为S,大气压强为p0。如图所示,气缸水平放置时,活塞与气缸底部的距离为L,现将气缸竖直放置,活塞将缓慢下降,不计活塞与气缸间的摩擦,不计气缸周围环境温度的变化,重力加速度为g,求活塞静止时到气缸底部的距离。
4.(2021山东菏泽期末)在两端封闭、粗细均匀的U形细玻璃管内有一段水银柱,水银柱的两端各封闭有一段空气。当U形管两端竖直朝上时,平视图如图甲所示,左、右两边空气柱的长度分别为l1=18.0 cm和l2=12.0 cm,左边气体的压强为12.0 cmHg。现将U形管缓慢平放在水平桌面上,俯视图如图乙所示。已知没有气体从管的一边通过水银逸入另一边,且整个过程中气体温度保持不变。求:U形管平放时两边空气柱的长度l'1、l'2。
题组二 查理定律
5.(2023上海长宁二模)一定质量的气体保持体积不变,温度由0 ℃升高到10 ℃时,其压强的增加量为Δp1;当温度由100 ℃升高到110 ℃时,其压强的增加量为Δp2。则Δp1与Δp2之比是 ( )
A.1∶1 B.1∶10
C.10∶110 D.273∶283
6.如图所示为一定质量气体的等容线,下面说法中正确的是 ( )
A.直线AB的斜率是
B.0 ℃时气体的压强为p0
C.温度在接近0 K时气体的压强为零
D.BA延长线与横轴交点横坐标为-273 ℃
7.(2021福建霞浦第一中学阶段练习)如图所示,四个两端封闭、粗细均匀的玻璃管内的空气被一段水银柱隔开,按图中标明的条件,当玻璃管水平放置时,水银柱处于静止状态。如果管内两端的空气都升高相同的温度,则水银柱向左移动的是 ( )
A
B
C
D
8.(2023山东临沂一模)某学习小组设计了一种测温装置,用于测量教室内的气温(教室内的气压为一个标准大气压,相当于76 cm汞柱产生的压强),结构如图所示,导热性能良好的大玻璃泡A内有一定量的气体,与A相连的B管插在水银槽中,B管内水银面的高度x可反映所处环境的温度,据此在B管上标注出温度的刻度值。当教室内温度为7 ℃时,B管内水银面的高度为20 cm。B管的体积与大玻璃泡A的体积相比可忽略不计,则以下说法正确的是( )
A.B管上所刻的温度数值上高下低
B.B管内水银面的高度为16 cm时,教室内的温度为17 ℃
C.B管上所标的温度数值间隔是不均匀的
D.若把这个已标注好温度值的装置移到高山上,测出的温度比实际温度偏高
9.(2022广东广州二模)如图,刚经过高温消毒的茶杯和杯盖,从消毒碗柜里取出后,茶杯放置在水平桌面上并立刻盖上杯盖,茶杯内密封温度为87 ℃、压强等于外界大气压强p0的气体。已知杯盖的质量为m,杯口面积为S,重力加速度为g。求茶杯内气体降温至27 ℃时,茶杯对杯盖的支持力大小。(取T=t+273 K)
题组三 盖—吕萨克定律
10.如图所示,某同学用封有气体的玻璃管来测绝对零度,当水温是30 ℃时,空气柱长度为30 cm,当水温是90 ℃时,空气柱的长度是36 cm,则该同学测得的绝对零度为 ( )
A.-273 ℃ B.-270 ℃
C.-268 ℃ D.-271 ℃
11.(2023广东茂名二模)小明想用易拉罐制作一个简易装置,用来判定环境温度是否发生变化。其做法是:向空的易拉罐插入一根粗细均匀的透明吸管,接口用石蜡密封,吸管内有一液滴封闭着可看作理想气体的空气,整个装置水平放置。在忽略大气压变化的情况下,下列说法正确的是 ( )
A.易拉罐不变,吸管越细,装置越灵敏
B.当液滴向右移动时,环境温度降低
C.当液滴向左移动时,易拉罐内气体内能减少
D.液滴向右移动过程中,易拉罐内气体分子运动激烈程度增大
12.(2021福建厦门集美中学期中)若一容器内气体的温度从7 ℃升高到47 ℃,而容器内气体压强不变,容器容积不变,则此时容器内的气体质量减少了 ( )
A.11.5% B.12.5% C.14.3% D.16.8%
13.(2023湖南岳阳适应性考试)如图所示,一足够高圆柱形容器竖直放置,通过活塞封闭着摄氏温度为t的理想气体。活塞的质量为m,横截面积为S,与容器底部相距h。现通过电热丝给气体加热一段时间,结果活塞缓慢上升了h,已知大气压强为p0,重力加速度为g,不计器壁向外散失的热量及活塞与器壁间的摩擦,取T=t+273 K,求:
(1)气体的压强;
(2)这段时间内气体的温度升高了多少
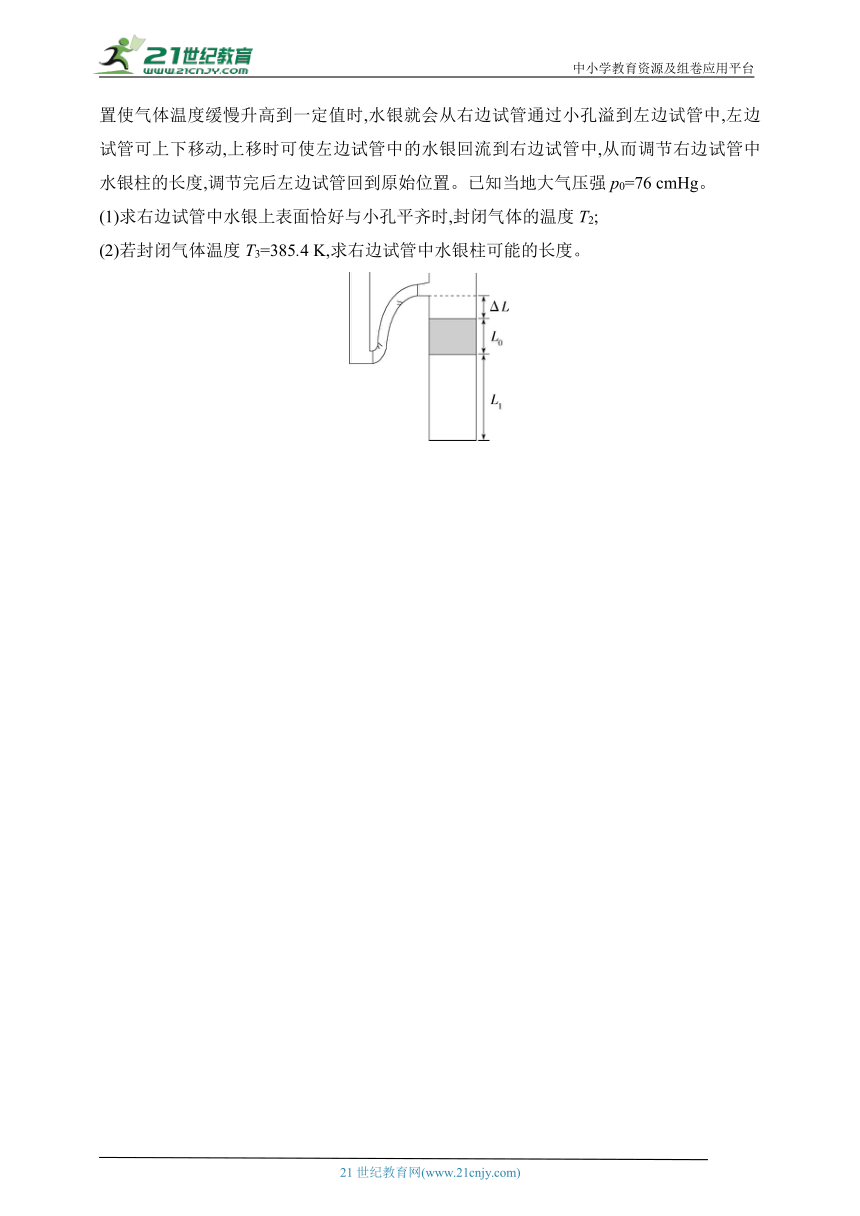
14.(2023山东日照期末)一竖直放置的圆柱形试管内,通过一段长L0=24 cm的水银柱封闭了一段理想气体,气柱高L1=60 cm、温度T1=300 K,水银的上表面与管侧面小孔的高度差ΔL=16 cm,小孔左边用一橡胶软管连接另一支上端开口的空试管,如图所示。通过加热装置使气体温度缓慢升高到一定值时,水银就会从右边试管通过小孔溢到左边试管中,左边试管可上下移动,上移时可使左边试管中的水银回流到右边试管中,从而调节右边试管中水银柱的长度,调节完后左边试管回到原始位置。已知当地大气压强p0=76 cmHg。
(1)求右边试管中水银上表面恰好与小孔平齐时,封闭气体的温度T2;
(2)若封闭气体温度T3=385.4 K,求右边试管中水银柱可能的长度。
能力提升练
题组一 液柱封闭类
1.(2022重庆八中期中)如图所示,一内径均匀的导热U形管竖直放置,右侧管口封闭,左侧上端与大气相通。一段水银柱D和一个光滑轻质活塞C将A、B两部分空气封在管内。初始稳定状态下,A气柱长度为lA=9 cm,B气柱长度为lB=6 cm,两管内水银面的高度差h=10 cm。已知大气压强恒为p0=76 cmHg,环境温度恒为T0=297 K。
(1)求初始稳定状态下B气体的压强pB;
(2)现仅对B气体缓慢加热,使B气体的温度为TB=627 K,求此时左、右管水银柱液面高度差;
(3)为使左右两管内液面等高,现仅用外力使活塞缓慢上移,求两液面等高时活塞移动的距离x(左侧管道足够长)。
2.(2021广东珠海模拟)某同学实验时将一根长L=1 m、粗细均匀的玻璃管竖直固定在升降机内,玻璃管上端开口下端封闭,在管内用h=46 cm的水银柱封闭着L1=50 cm的空气柱。若忽略升降机内环境温度的变化,升降机内大气压强恒为p0=74 cmHg,取g=10 m/s2,现在升降机先以a=3.5 m/s2的加速度匀加速下降一段时间后,再以相同大小的加速度匀减速下降,求两种状态下稳定时被封闭空气柱的长度分别为多少 (结果保留两位有效数字)
题组二 活塞封闭类
3.(2023山东济宁一模)如图甲所示,两端开口的导热气缸水平固定,A、B是厚度不计的两轻活塞,可在气缸内无摩擦滑动,缸内有理想气体。A、B静止时,缸内两部分的气柱长分别为L和;劲度系数k=的轻弹簧,一端连接活塞A、一端固定在位于活塞A左侧的O点(图中未画出),且为原长。现用轻质细线将活塞B与重物C拴接,如图乙所示,一段时间后活塞A、B再次静止。已知活塞A、B面积S1、S2的关系为S1=2S2=2S,大气压强为p0,重力加速度为g,重物C的质量为m=,环境和缸内气体温度T1=300 K。两活塞再次静止时,求:
(1)气缸内气体的压强;
(2)活塞B移动的距离x。
甲
乙
4.(2022山东济南外国语学校检测)如图,一竖直放置的气缸上端开口,气缸壁内有卡口a和b,a、b间距为h,a距缸底的高度为H;活塞只能在a、b间移动,其下方密封有一定质量的理想气体。已知活塞质量为m,横截面积为S,厚度可忽略;活塞和气缸壁均绝热,不计它们之间的摩擦。开始时活塞处于静止状态,上、下方气体压强均为p0,温度均为T0。现用电热丝缓慢加热气缸中的气体,直至活塞刚好到达b处。求此时气缸内气体的温度以及在此过程中气体对外所做的功。(重力加速度大小为g)
题组三 充放气问题中气体实验定律的应用
5.(2022重庆阶段练习)可折叠轮椅的发明为参加北京冬残奥会的运动员的出行提供了便利。该轮椅只需简单几步,就能缩至不到20 L放入拉杆箱中,并可带上飞机放入行李舱。若轮椅折叠收入箱中时,轮胎中空气全部被排尽,打开使用时需重新充气。已知大气压强为p0且保持不变,某次在室温下(27 ℃)对轮胎充气,使轮胎内压强达到4p0。单边轮胎充满气时内部气体体积为V0,且充满后轮胎不漏气。
(1)若打气筒每次充入0.1V0的压强为p0的空气,则对单边轮胎共需打气多少次
(2)若运动员坐上轮椅后,轮胎内气体体积变为V0,要使轮胎内压强不超过4.5p0,则行驶时胎内气体温度应不超过多少摄氏度 (不考虑行驶过程中胎内气体体积的变化,取T=t+273 K)
6.(2021辽宁朝阳一模)如图所示是某种防疫消毒用的喷雾消毒桶的原理图。消毒桶的总容积为10 L,装入7 L的药液后再用密封盖将消毒桶密封,与消毒桶相连的活塞式打气筒每次能压入250 cm3的1 atm的空气,设整个过程温度保持不变,求:
(1)要使消毒桶中空气的压强达到5 atm,打气筒应打压几次
(2)在消毒桶中空气的压强达到5 atm时,打开喷嘴使其喷雾,直到内、外气体压强相等时不再向外喷消毒液,消毒桶内是否还剩消毒液 如果剩下的话,还剩下多少体积的消毒液 如果剩不下了,喷出去的气体质量占原来喷消毒液前消毒桶内气体质量的多少
第5节 气体实验定律
基础过关练
1.CD 2.ABD 5.A 6.ABD 7.CD 8.D
10.B 11.ACD 12.B
1.CD 氢气球上升时,可以认为是等温变化的过程,由于高空处空气稀薄,球外空气的压强小,球内气体要膨胀,到一定程度时,气球就会胀破,故选C、D。
2.ABD 一定质量的气体的等温线为双曲线的一支,由等温线的物理意义可知,压强与体积成反比,在不同温度下的等温线是不同的,所以A、B正确;对于一定质量的气体,温度越高,等温线离坐标原点的位置就越远,故C错误,D正确。
导师点睛 一定质量的气体的p-V图像规律
(1)不同的等温线温度不同,越靠近原点的等温线温度越低,越远离原点的等温线温度越高。
(2)由不同等温线的分布情况可以判断温度的高低。
3.答案 L
解析 由于气缸导热,且不计环境温度的变化,将气缸由水平放置变成竖直放置,直到活塞不再下降的过程中,缸内密闭气体经历的是等温过程,设此时活塞到气缸底部的距离为h
气缸水平放置时,对活塞有:p1S-p0S=0
气缸竖直放置后活塞静止时,对活塞有
p2S-mg-p0S=0
对上述过程中的气体,根据玻意耳定律有:p1LS=p2hS
联立解得:h=L。
方法技巧 应用玻意耳定律的思路和方法
(1)确定研究对象,并判断是否满足玻意耳定律成立的条件。
(2)确定始末状态及状态参量(p1、V1,p2、V2)。
(3)根据玻意耳定律列方程p1V1=p2V2,代入数值求解(注意各状态参量要统一单位)。
(4)注意分析题目中的隐含条件,必要时还应由力学或几何知识列出辅助方程。
(5)有时要检验结果是否符合实际,对不符合实际的结果要舍去。
4.答案 22.5 cm 7.5 cm
解析 设U形管两端竖直朝上时,左、右两边气体的压强分别为p1和p2。
由力的平衡条件有p1=p2+ρg(l1-l2)
式中ρ为水银密度,g为重力加速度大小
U形管水平放置时,两边气体压强相等,设为p,此时原左、右两边气柱长度分别变为l'1和l'2。
由玻意耳定律有p1l1=pl'1,p2l2=pl'2
两边气柱长度的变化量大小相等,设为x,x=l'1-l1=l2-l'2
联立得x=4.5 cm,l'1=22.5 cm,l'2=7.5 cm。
5.A 一定质量的气体保持体积不变,根据查理定律的推论式有=,两种情况温度变化量相同,故可得Δp1=Δp2,Δp1∶Δp2=1∶1,故选A。
6.ABD 在p-t图像上,等容线的延长线与t轴的交点横坐标为-273 ℃,从图中可以看出,0 ℃时气体压强为p0,因此直线AB的斜率为,A、B、D正确;在接近0 K时,气体已变为液态或固态,因此不满足查理定律,压强不为零,C错误。
7.CD 假设温度升高,水银柱不动,两边气体均做等容变化,根据查理定律可得压强的增加量Δp=p,而左右两边初态压强p相同,两边温度升高量ΔT也相同,所以Δp跟成正比,即左右两边气体初态温度T越高,气体压强的增加量Δp越小,水银柱应向气体压强增加量小的方向移动,即应向初态温度高的一侧移动,根据以上分析,A图中,TaTb,水银柱应向左移动;D图中,Ta>Tb,水银柱应向左移动,A、B错误,C、D正确。
8.D 当温度升高时,管内气体体积变大,B管液面降低,则B管上所刻的温度数值上低下高,故A错误;B管的体积与大玻璃泡A的体积相比可忽略不计,可认为气体做等容变化,则当温度为7 ℃时,有T1=273 K+7 K=280 K,玻璃泡A内气体压强为p1=76 cmHg-20 cmHg=56 cmHg,温度改变为T2时,气体压强为p2=76 cmHg-16 cmHg=60 cmHg,根据=可得T2=300 K=27 ℃,选项B错误;温度改变为T时,气体压强为p=76-x(cmHg),根据=可得T=380-5x(K),则B管上所标的温度数值间隔是均匀的,选项C错误;若把这个已经刻好温度值的装置移到高山上,大气压强比地面偏小,导致A内体积偏大,管内液面下降,则测出的温度比实际温度偏高,故D正确。
9.答案 p0S+mg
解析 茶杯内气体初始温度为T1=(87+273)K=360 K
气体末状态温度为T2=(27+273)K=300 K
杯内封闭气体发生等容变化,由查理定律有=
代入数据解得,末态杯内气体的压强p'=p0
对杯盖,由平衡条件有p'S+N=p0S+mg
解得N=p0S+mg
10.B 设绝对零度为T0 ,则T1=-T0+30 ℃,V1=30 cm×S,T2=-T0+90 ℃,V2=36 cm×S ,由盖—吕萨克定律得=,代入数据解得T0=-270 ℃ ,故B正确。
11.ACD 由题意可知,罐内气体做等压变化,由盖—吕萨克定律=可知,当罐内气体温度升高时,气体的体积增大,吸管内的液滴向右移动,则吸管上的温度刻度值左小右大。由V=Sl可得,当易拉罐不变,温度变化相同时,体积变化相同,吸管越细,液滴移动距离越大,所以装置越灵敏,A正确;当液滴向右移动时,气体的体积增大,由盖—吕萨克定律可知,环境温度升高,则易拉罐内气体分子运动激烈程度增大,B错误,D正确;当液滴向左移动时,气体的体积减小,由盖—吕萨克定律可知,环境温度降低,则易拉罐内气体内能减少,C正确。故选A、C、D。
12.B 根据盖—吕萨克定律可知
=
解得=
则容器内的气体质量减少了
==12.5%
故选B。
13.答案 (1)p0+ (2)273 K+t
解析 (1)设气体的压强为p,以活塞为研究对象,受力分析得:pS=p0S+mg
解得气体的压强为p=p0+。
(2)设加热后气体的摄氏温度为t',以被封闭的气体为研究对象,气体经历等压变化
初状态:V1=hS,T1=273 K+t
末状态:V2=2hS,T2=273 K+t'
由盖—吕萨克定律=
得:=
解得t'=273 K+2t
Δt=t'-t=273 K+t。
14.答案 (1)380 K (2)6 cm或18 cm
解析 (1)被封闭气体从初始状态到水银上表面恰好与小孔平齐的过程中,压强p1不变,设右侧试管横截面积为S,则根据盖—吕萨克定律=,解得T2=380 K。
(2)假设右侧水银不会进入左侧,则封闭气体从T1升到T3是等压过程,则根据盖—吕萨克定律得=,解得L3=77.08 cm,因为77.08 cm+24 cm>60 cm+16 cm+24 cm,所以此时右边试管中水银柱上表面已经超过了小孔的位置,即假设不成立,实际有一部分水银流到了左侧,设右边试管中水银柱剩余长度为x,封闭气体长度为L4,压强为p4,则
联立解得x=6 cm或x=18 cm
能力提升练
1.答案 (1)66 cmHg (2)0 (3)15 cm
解析 (1)由题意知B部分气体稳定状态下的压强pB=pA-ρgh=p0-ρgh=66 cmHg。
(2)设U形管的横截面积为S,B气体的温度TB=627 K时,右管水银柱下降Δh
B部分气体初状态压强pB=66 cmHg,体积VB=lBS,温度T0=297 K
末状态压强p'B=p0-ρg(h-2Δh),体积V'B=(lB+Δh)S
由理想气体状态方程得=
联立解得Δh=5 cm,由初始状态两管内水银面的高度差h=10 cm知,此时左右管水银柱液面高度差为0。
(3)A部分气体初状态压强pA=76 cmHg,体积为VA=lAS
末状态压强为p'A,体积V'A=l'AS
B部分气体初状态压强pB=66 cmHg,体积为VB=lBS末状态压强pB2=p'A,体积VB2=S
根据玻意耳定律有pAVA=p'AV'A,pBVB=pB2VB2
解得l'A=19 cm
所以活塞在管中移动的距离
x=l'A-lA+=19 cm-9 cm+ cm=15 cm。
2.答案 60 cm 47 cm
解析 升降机静止时,水银柱产生的压强p==ρgh
升降机加速下降时水银柱产生的压强p1==ρ(g-a)h
解得p1=p=29.9 cmHg
气体发生等温变化,由玻意耳定律可得
(p0+p)L1S=(p0+p1)L2S
解得L2≈58 cm,由于L2+h>L
因此升降机加速下降时,玻璃管内有水银溢出,设剩余水银长度为x,则剩余水银在静止时产生的压强为px=ρgx,由玻意耳定律可得
(p0+p)L1S=(L-x)S
解得x=40 cm,此时空气柱长度为L3=L-x=60 cm
若升降机静止,x=40 cm的水银柱产生的压强为px=40 cmHg,升降机匀减速下降时,水银柱产生的压强为p3=px=54 cmHg
气体发生等温变化,由玻意耳定律可得
(p0+p)L1S=(p0+p3)L4S
联立解得L4≈47 cm。
3.答案 (1)p0 (2)L
解析 (1)活塞重新静止时,对活塞B受力分析可知
pS+mg=p0S
解得p=p0。
(2)对活塞A,由平衡条件得p0·2S=p·2S+kΔx
解得弹簧的形变量Δx=L
对缸内气体,根据玻意耳定律有
p0=p
解得x=L
4.答案 T0 (p0S+mg)h
解析 开始时活塞位于a处,加热后,气缸中的气体先经历等容过程,直至活塞开始运动。设活塞刚要运动时气缸中气体的温度为T1,压强为p1,根据查理定律有
= ①
根据力的平衡条件有p1S=p0S+mg ②
联立可得T1=T0 ③
此后,气缸中的气体经历等压过程,直至活塞刚好到达b处,设此时气缸中气体的温度为T2;设活塞位于a处和b处时气体的体积分别为V1和V2。根据盖—吕萨克定律有= ④
式中V1=SH,V2=S(H+h) ⑤
联立③④⑤式解得T2=T0
从开始加热到活塞到达b处的过程中,气缸中的气体对外做的功为W=(p0S+mg)h
方法技巧 本题可直接对气缸内的理想气体用理想气体状态方程,=,结合活塞的平衡条件p1S=p0S+mg,能更简便获得结果。
5.答案 (1)40 (2)42 ℃
解析 (1)在室温下对轮胎充气,由玻意耳定律可得np0×0.1V0=4p0V0
解得n=40次
(2)设运动员坐上轮椅后轮胎内气体压强为p',由玻意耳定律可得4p0V0=p'×V0
行驶过程中胎内气体体积不变,由查理定律可得=
联立可得t=42 ℃
6.答案 (1)48 (2)剩不下
解析 (1)设需打压n次才能使消毒桶内气体压强变为5 atm,由玻意耳定律得
p1(V1+nΔV)=p2V1
其中p1=1 atm,p2=5 atm,V1=10 L-7 L=3 L,ΔV=250 cm3=0.25 L
将已知量代入得n=48(次)
(2)停止喷雾时,桶内气体压强变为1 atm,此时气体体积为V2
由玻意耳定律得p2V1=p1V2
即5 atm×3 L=1 atm×V2
解得V2=15 L
大于消毒桶的总容积10 L,故消毒桶里没有剩下消毒液。喷出去气体体积
ΔV=15 L-10 L=5 L
则==
方法技巧 充气、放气和分装问题的处理技巧
(1)充气问题
向球、轮胎中充气是一个典型的变质量的气体问题。只要选择球内原有气体和即将打入的气体作为研究对象,就可把充气过程中气体质量变化的问题转化为定质量问题。
(2)抽气问题
从容器内抽气的过程中,容器内的气体质量不断减小,这属于变质量问题。分析时,将每次抽气过程中抽出的气体和剩余气体作为研究对象,质量不变,故抽气过程可看作是等温膨胀过程。
(3)分装问题
将一个大容器里的气体分装到多个小容器中的问题也是一个典型的变质量问题。分析这类问题时,可以把大容器中的气体和多个小容器中的气体看作整体研究,可将变质量问题转化为定质量问题,运用相关规律求解。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024鲁科版高中物理选择性必修第三册同步
第5节 气体实验定律
基础过关练
题组一 玻意耳定律
1.各种卡通形状的氢气球受到孩子们的喜欢,若孩子一不小心松手,氢气球会飞向天空,上升到一定高度会胀破,关于其胀破的原因,下列说法中正确的是 ( )
A.球内氢气温度升高
B.球内氢气压强增大
C.球内气体体积增大
D.球内外的压力差超过球的承受限度
2.如图所示为一定质量的气体在不同温度下的两条等温线,则下列说法中正确的是( )
A.一定质量的气体在发生等温变化时,其压强与体积成反比
B.一定质量的气体,在不同温度下的等温线是不同的
C.T1>T2
D.T1
4.(2021山东菏泽期末)在两端封闭、粗细均匀的U形细玻璃管内有一段水银柱,水银柱的两端各封闭有一段空气。当U形管两端竖直朝上时,平视图如图甲所示,左、右两边空气柱的长度分别为l1=18.0 cm和l2=12.0 cm,左边气体的压强为12.0 cmHg。现将U形管缓慢平放在水平桌面上,俯视图如图乙所示。已知没有气体从管的一边通过水银逸入另一边,且整个过程中气体温度保持不变。求:U形管平放时两边空气柱的长度l'1、l'2。
题组二 查理定律
5.(2023上海长宁二模)一定质量的气体保持体积不变,温度由0 ℃升高到10 ℃时,其压强的增加量为Δp1;当温度由100 ℃升高到110 ℃时,其压强的增加量为Δp2。则Δp1与Δp2之比是 ( )
A.1∶1 B.1∶10
C.10∶110 D.273∶283
6.如图所示为一定质量气体的等容线,下面说法中正确的是 ( )
A.直线AB的斜率是
B.0 ℃时气体的压强为p0
C.温度在接近0 K时气体的压强为零
D.BA延长线与横轴交点横坐标为-273 ℃
7.(2021福建霞浦第一中学阶段练习)如图所示,四个两端封闭、粗细均匀的玻璃管内的空气被一段水银柱隔开,按图中标明的条件,当玻璃管水平放置时,水银柱处于静止状态。如果管内两端的空气都升高相同的温度,则水银柱向左移动的是 ( )
A
B
C
D
8.(2023山东临沂一模)某学习小组设计了一种测温装置,用于测量教室内的气温(教室内的气压为一个标准大气压,相当于76 cm汞柱产生的压强),结构如图所示,导热性能良好的大玻璃泡A内有一定量的气体,与A相连的B管插在水银槽中,B管内水银面的高度x可反映所处环境的温度,据此在B管上标注出温度的刻度值。当教室内温度为7 ℃时,B管内水银面的高度为20 cm。B管的体积与大玻璃泡A的体积相比可忽略不计,则以下说法正确的是( )
A.B管上所刻的温度数值上高下低
B.B管内水银面的高度为16 cm时,教室内的温度为17 ℃
C.B管上所标的温度数值间隔是不均匀的
D.若把这个已标注好温度值的装置移到高山上,测出的温度比实际温度偏高
9.(2022广东广州二模)如图,刚经过高温消毒的茶杯和杯盖,从消毒碗柜里取出后,茶杯放置在水平桌面上并立刻盖上杯盖,茶杯内密封温度为87 ℃、压强等于外界大气压强p0的气体。已知杯盖的质量为m,杯口面积为S,重力加速度为g。求茶杯内气体降温至27 ℃时,茶杯对杯盖的支持力大小。(取T=t+273 K)
题组三 盖—吕萨克定律
10.如图所示,某同学用封有气体的玻璃管来测绝对零度,当水温是30 ℃时,空气柱长度为30 cm,当水温是90 ℃时,空气柱的长度是36 cm,则该同学测得的绝对零度为 ( )
A.-273 ℃ B.-270 ℃
C.-268 ℃ D.-271 ℃
11.(2023广东茂名二模)小明想用易拉罐制作一个简易装置,用来判定环境温度是否发生变化。其做法是:向空的易拉罐插入一根粗细均匀的透明吸管,接口用石蜡密封,吸管内有一液滴封闭着可看作理想气体的空气,整个装置水平放置。在忽略大气压变化的情况下,下列说法正确的是 ( )
A.易拉罐不变,吸管越细,装置越灵敏
B.当液滴向右移动时,环境温度降低
C.当液滴向左移动时,易拉罐内气体内能减少
D.液滴向右移动过程中,易拉罐内气体分子运动激烈程度增大
12.(2021福建厦门集美中学期中)若一容器内气体的温度从7 ℃升高到47 ℃,而容器内气体压强不变,容器容积不变,则此时容器内的气体质量减少了 ( )
A.11.5% B.12.5% C.14.3% D.16.8%
13.(2023湖南岳阳适应性考试)如图所示,一足够高圆柱形容器竖直放置,通过活塞封闭着摄氏温度为t的理想气体。活塞的质量为m,横截面积为S,与容器底部相距h。现通过电热丝给气体加热一段时间,结果活塞缓慢上升了h,已知大气压强为p0,重力加速度为g,不计器壁向外散失的热量及活塞与器壁间的摩擦,取T=t+273 K,求:
(1)气体的压强;
(2)这段时间内气体的温度升高了多少
14.(2023山东日照期末)一竖直放置的圆柱形试管内,通过一段长L0=24 cm的水银柱封闭了一段理想气体,气柱高L1=60 cm、温度T1=300 K,水银的上表面与管侧面小孔的高度差ΔL=16 cm,小孔左边用一橡胶软管连接另一支上端开口的空试管,如图所示。通过加热装置使气体温度缓慢升高到一定值时,水银就会从右边试管通过小孔溢到左边试管中,左边试管可上下移动,上移时可使左边试管中的水银回流到右边试管中,从而调节右边试管中水银柱的长度,调节完后左边试管回到原始位置。已知当地大气压强p0=76 cmHg。
(1)求右边试管中水银上表面恰好与小孔平齐时,封闭气体的温度T2;
(2)若封闭气体温度T3=385.4 K,求右边试管中水银柱可能的长度。
能力提升练
题组一 液柱封闭类
1.(2022重庆八中期中)如图所示,一内径均匀的导热U形管竖直放置,右侧管口封闭,左侧上端与大气相通。一段水银柱D和一个光滑轻质活塞C将A、B两部分空气封在管内。初始稳定状态下,A气柱长度为lA=9 cm,B气柱长度为lB=6 cm,两管内水银面的高度差h=10 cm。已知大气压强恒为p0=76 cmHg,环境温度恒为T0=297 K。
(1)求初始稳定状态下B气体的压强pB;
(2)现仅对B气体缓慢加热,使B气体的温度为TB=627 K,求此时左、右管水银柱液面高度差;
(3)为使左右两管内液面等高,现仅用外力使活塞缓慢上移,求两液面等高时活塞移动的距离x(左侧管道足够长)。
2.(2021广东珠海模拟)某同学实验时将一根长L=1 m、粗细均匀的玻璃管竖直固定在升降机内,玻璃管上端开口下端封闭,在管内用h=46 cm的水银柱封闭着L1=50 cm的空气柱。若忽略升降机内环境温度的变化,升降机内大气压强恒为p0=74 cmHg,取g=10 m/s2,现在升降机先以a=3.5 m/s2的加速度匀加速下降一段时间后,再以相同大小的加速度匀减速下降,求两种状态下稳定时被封闭空气柱的长度分别为多少 (结果保留两位有效数字)
题组二 活塞封闭类
3.(2023山东济宁一模)如图甲所示,两端开口的导热气缸水平固定,A、B是厚度不计的两轻活塞,可在气缸内无摩擦滑动,缸内有理想气体。A、B静止时,缸内两部分的气柱长分别为L和;劲度系数k=的轻弹簧,一端连接活塞A、一端固定在位于活塞A左侧的O点(图中未画出),且为原长。现用轻质细线将活塞B与重物C拴接,如图乙所示,一段时间后活塞A、B再次静止。已知活塞A、B面积S1、S2的关系为S1=2S2=2S,大气压强为p0,重力加速度为g,重物C的质量为m=,环境和缸内气体温度T1=300 K。两活塞再次静止时,求:
(1)气缸内气体的压强;
(2)活塞B移动的距离x。
甲
乙
4.(2022山东济南外国语学校检测)如图,一竖直放置的气缸上端开口,气缸壁内有卡口a和b,a、b间距为h,a距缸底的高度为H;活塞只能在a、b间移动,其下方密封有一定质量的理想气体。已知活塞质量为m,横截面积为S,厚度可忽略;活塞和气缸壁均绝热,不计它们之间的摩擦。开始时活塞处于静止状态,上、下方气体压强均为p0,温度均为T0。现用电热丝缓慢加热气缸中的气体,直至活塞刚好到达b处。求此时气缸内气体的温度以及在此过程中气体对外所做的功。(重力加速度大小为g)
题组三 充放气问题中气体实验定律的应用
5.(2022重庆阶段练习)可折叠轮椅的发明为参加北京冬残奥会的运动员的出行提供了便利。该轮椅只需简单几步,就能缩至不到20 L放入拉杆箱中,并可带上飞机放入行李舱。若轮椅折叠收入箱中时,轮胎中空气全部被排尽,打开使用时需重新充气。已知大气压强为p0且保持不变,某次在室温下(27 ℃)对轮胎充气,使轮胎内压强达到4p0。单边轮胎充满气时内部气体体积为V0,且充满后轮胎不漏气。
(1)若打气筒每次充入0.1V0的压强为p0的空气,则对单边轮胎共需打气多少次
(2)若运动员坐上轮椅后,轮胎内气体体积变为V0,要使轮胎内压强不超过4.5p0,则行驶时胎内气体温度应不超过多少摄氏度 (不考虑行驶过程中胎内气体体积的变化,取T=t+273 K)
6.(2021辽宁朝阳一模)如图所示是某种防疫消毒用的喷雾消毒桶的原理图。消毒桶的总容积为10 L,装入7 L的药液后再用密封盖将消毒桶密封,与消毒桶相连的活塞式打气筒每次能压入250 cm3的1 atm的空气,设整个过程温度保持不变,求:
(1)要使消毒桶中空气的压强达到5 atm,打气筒应打压几次
(2)在消毒桶中空气的压强达到5 atm时,打开喷嘴使其喷雾,直到内、外气体压强相等时不再向外喷消毒液,消毒桶内是否还剩消毒液 如果剩下的话,还剩下多少体积的消毒液 如果剩不下了,喷出去的气体质量占原来喷消毒液前消毒桶内气体质量的多少
第5节 气体实验定律
基础过关练
1.CD 2.ABD 5.A 6.ABD 7.CD 8.D
10.B 11.ACD 12.B
1.CD 氢气球上升时,可以认为是等温变化的过程,由于高空处空气稀薄,球外空气的压强小,球内气体要膨胀,到一定程度时,气球就会胀破,故选C、D。
2.ABD 一定质量的气体的等温线为双曲线的一支,由等温线的物理意义可知,压强与体积成反比,在不同温度下的等温线是不同的,所以A、B正确;对于一定质量的气体,温度越高,等温线离坐标原点的位置就越远,故C错误,D正确。
导师点睛 一定质量的气体的p-V图像规律
(1)不同的等温线温度不同,越靠近原点的等温线温度越低,越远离原点的等温线温度越高。
(2)由不同等温线的分布情况可以判断温度的高低。
3.答案 L
解析 由于气缸导热,且不计环境温度的变化,将气缸由水平放置变成竖直放置,直到活塞不再下降的过程中,缸内密闭气体经历的是等温过程,设此时活塞到气缸底部的距离为h
气缸水平放置时,对活塞有:p1S-p0S=0
气缸竖直放置后活塞静止时,对活塞有
p2S-mg-p0S=0
对上述过程中的气体,根据玻意耳定律有:p1LS=p2hS
联立解得:h=L。
方法技巧 应用玻意耳定律的思路和方法
(1)确定研究对象,并判断是否满足玻意耳定律成立的条件。
(2)确定始末状态及状态参量(p1、V1,p2、V2)。
(3)根据玻意耳定律列方程p1V1=p2V2,代入数值求解(注意各状态参量要统一单位)。
(4)注意分析题目中的隐含条件,必要时还应由力学或几何知识列出辅助方程。
(5)有时要检验结果是否符合实际,对不符合实际的结果要舍去。
4.答案 22.5 cm 7.5 cm
解析 设U形管两端竖直朝上时,左、右两边气体的压强分别为p1和p2。
由力的平衡条件有p1=p2+ρg(l1-l2)
式中ρ为水银密度,g为重力加速度大小
U形管水平放置时,两边气体压强相等,设为p,此时原左、右两边气柱长度分别变为l'1和l'2。
由玻意耳定律有p1l1=pl'1,p2l2=pl'2
两边气柱长度的变化量大小相等,设为x,x=l'1-l1=l2-l'2
联立得x=4.5 cm,l'1=22.5 cm,l'2=7.5 cm。
5.A 一定质量的气体保持体积不变,根据查理定律的推论式有=,两种情况温度变化量相同,故可得Δp1=Δp2,Δp1∶Δp2=1∶1,故选A。
6.ABD 在p-t图像上,等容线的延长线与t轴的交点横坐标为-273 ℃,从图中可以看出,0 ℃时气体压强为p0,因此直线AB的斜率为,A、B、D正确;在接近0 K时,气体已变为液态或固态,因此不满足查理定律,压强不为零,C错误。
7.CD 假设温度升高,水银柱不动,两边气体均做等容变化,根据查理定律可得压强的增加量Δp=p,而左右两边初态压强p相同,两边温度升高量ΔT也相同,所以Δp跟成正比,即左右两边气体初态温度T越高,气体压强的增加量Δp越小,水银柱应向气体压强增加量小的方向移动,即应向初态温度高的一侧移动,根据以上分析,A图中,Ta
8.D 当温度升高时,管内气体体积变大,B管液面降低,则B管上所刻的温度数值上低下高,故A错误;B管的体积与大玻璃泡A的体积相比可忽略不计,可认为气体做等容变化,则当温度为7 ℃时,有T1=273 K+7 K=280 K,玻璃泡A内气体压强为p1=76 cmHg-20 cmHg=56 cmHg,温度改变为T2时,气体压强为p2=76 cmHg-16 cmHg=60 cmHg,根据=可得T2=300 K=27 ℃,选项B错误;温度改变为T时,气体压强为p=76-x(cmHg),根据=可得T=380-5x(K),则B管上所标的温度数值间隔是均匀的,选项C错误;若把这个已经刻好温度值的装置移到高山上,大气压强比地面偏小,导致A内体积偏大,管内液面下降,则测出的温度比实际温度偏高,故D正确。
9.答案 p0S+mg
解析 茶杯内气体初始温度为T1=(87+273)K=360 K
气体末状态温度为T2=(27+273)K=300 K
杯内封闭气体发生等容变化,由查理定律有=
代入数据解得,末态杯内气体的压强p'=p0
对杯盖,由平衡条件有p'S+N=p0S+mg
解得N=p0S+mg
10.B 设绝对零度为T0 ,则T1=-T0+30 ℃,V1=30 cm×S,T2=-T0+90 ℃,V2=36 cm×S ,由盖—吕萨克定律得=,代入数据解得T0=-270 ℃ ,故B正确。
11.ACD 由题意可知,罐内气体做等压变化,由盖—吕萨克定律=可知,当罐内气体温度升高时,气体的体积增大,吸管内的液滴向右移动,则吸管上的温度刻度值左小右大。由V=Sl可得,当易拉罐不变,温度变化相同时,体积变化相同,吸管越细,液滴移动距离越大,所以装置越灵敏,A正确;当液滴向右移动时,气体的体积增大,由盖—吕萨克定律可知,环境温度升高,则易拉罐内气体分子运动激烈程度增大,B错误,D正确;当液滴向左移动时,气体的体积减小,由盖—吕萨克定律可知,环境温度降低,则易拉罐内气体内能减少,C正确。故选A、C、D。
12.B 根据盖—吕萨克定律可知
=
解得=
则容器内的气体质量减少了
==12.5%
故选B。
13.答案 (1)p0+ (2)273 K+t
解析 (1)设气体的压强为p,以活塞为研究对象,受力分析得:pS=p0S+mg
解得气体的压强为p=p0+。
(2)设加热后气体的摄氏温度为t',以被封闭的气体为研究对象,气体经历等压变化
初状态:V1=hS,T1=273 K+t
末状态:V2=2hS,T2=273 K+t'
由盖—吕萨克定律=
得:=
解得t'=273 K+2t
Δt=t'-t=273 K+t。
14.答案 (1)380 K (2)6 cm或18 cm
解析 (1)被封闭气体从初始状态到水银上表面恰好与小孔平齐的过程中,压强p1不变,设右侧试管横截面积为S,则根据盖—吕萨克定律=,解得T2=380 K。
(2)假设右侧水银不会进入左侧,则封闭气体从T1升到T3是等压过程,则根据盖—吕萨克定律得=,解得L3=77.08 cm,因为77.08 cm+24 cm>60 cm+16 cm+24 cm,所以此时右边试管中水银柱上表面已经超过了小孔的位置,即假设不成立,实际有一部分水银流到了左侧,设右边试管中水银柱剩余长度为x,封闭气体长度为L4,压强为p4,则
联立解得x=6 cm或x=18 cm
能力提升练
1.答案 (1)66 cmHg (2)0 (3)15 cm
解析 (1)由题意知B部分气体稳定状态下的压强pB=pA-ρgh=p0-ρgh=66 cmHg。
(2)设U形管的横截面积为S,B气体的温度TB=627 K时,右管水银柱下降Δh
B部分气体初状态压强pB=66 cmHg,体积VB=lBS,温度T0=297 K
末状态压强p'B=p0-ρg(h-2Δh),体积V'B=(lB+Δh)S
由理想气体状态方程得=
联立解得Δh=5 cm,由初始状态两管内水银面的高度差h=10 cm知,此时左右管水银柱液面高度差为0。
(3)A部分气体初状态压强pA=76 cmHg,体积为VA=lAS
末状态压强为p'A,体积V'A=l'AS
B部分气体初状态压强pB=66 cmHg,体积为VB=lBS末状态压强pB2=p'A,体积VB2=S
根据玻意耳定律有pAVA=p'AV'A,pBVB=pB2VB2
解得l'A=19 cm
所以活塞在管中移动的距离
x=l'A-lA+=19 cm-9 cm+ cm=15 cm。
2.答案 60 cm 47 cm
解析 升降机静止时,水银柱产生的压强p==ρgh
升降机加速下降时水银柱产生的压强p1==ρ(g-a)h
解得p1=p=29.9 cmHg
气体发生等温变化,由玻意耳定律可得
(p0+p)L1S=(p0+p1)L2S
解得L2≈58 cm,由于L2+h>L
因此升降机加速下降时,玻璃管内有水银溢出,设剩余水银长度为x,则剩余水银在静止时产生的压强为px=ρgx,由玻意耳定律可得
(p0+p)L1S=(L-x)S
解得x=40 cm,此时空气柱长度为L3=L-x=60 cm
若升降机静止,x=40 cm的水银柱产生的压强为px=40 cmHg,升降机匀减速下降时,水银柱产生的压强为p3=px=54 cmHg
气体发生等温变化,由玻意耳定律可得
(p0+p)L1S=(p0+p3)L4S
联立解得L4≈47 cm。
3.答案 (1)p0 (2)L
解析 (1)活塞重新静止时,对活塞B受力分析可知
pS+mg=p0S
解得p=p0。
(2)对活塞A,由平衡条件得p0·2S=p·2S+kΔx
解得弹簧的形变量Δx=L
对缸内气体,根据玻意耳定律有
p0=p
解得x=L
4.答案 T0 (p0S+mg)h
解析 开始时活塞位于a处,加热后,气缸中的气体先经历等容过程,直至活塞开始运动。设活塞刚要运动时气缸中气体的温度为T1,压强为p1,根据查理定律有
= ①
根据力的平衡条件有p1S=p0S+mg ②
联立可得T1=T0 ③
此后,气缸中的气体经历等压过程,直至活塞刚好到达b处,设此时气缸中气体的温度为T2;设活塞位于a处和b处时气体的体积分别为V1和V2。根据盖—吕萨克定律有= ④
式中V1=SH,V2=S(H+h) ⑤
联立③④⑤式解得T2=T0
从开始加热到活塞到达b处的过程中,气缸中的气体对外做的功为W=(p0S+mg)h
方法技巧 本题可直接对气缸内的理想气体用理想气体状态方程,=,结合活塞的平衡条件p1S=p0S+mg,能更简便获得结果。
5.答案 (1)40 (2)42 ℃
解析 (1)在室温下对轮胎充气,由玻意耳定律可得np0×0.1V0=4p0V0
解得n=40次
(2)设运动员坐上轮椅后轮胎内气体压强为p',由玻意耳定律可得4p0V0=p'×V0
行驶过程中胎内气体体积不变,由查理定律可得=
联立可得t=42 ℃
6.答案 (1)48 (2)剩不下
解析 (1)设需打压n次才能使消毒桶内气体压强变为5 atm,由玻意耳定律得
p1(V1+nΔV)=p2V1
其中p1=1 atm,p2=5 atm,V1=10 L-7 L=3 L,ΔV=250 cm3=0.25 L
将已知量代入得n=48(次)
(2)停止喷雾时,桶内气体压强变为1 atm,此时气体体积为V2
由玻意耳定律得p2V1=p1V2
即5 atm×3 L=1 atm×V2
解得V2=15 L
大于消毒桶的总容积10 L,故消毒桶里没有剩下消毒液。喷出去气体体积
ΔV=15 L-10 L=5 L
则==
方法技巧 充气、放气和分装问题的处理技巧
(1)充气问题
向球、轮胎中充气是一个典型的变质量的气体问题。只要选择球内原有气体和即将打入的气体作为研究对象,就可把充气过程中气体质量变化的问题转化为定质量问题。
(2)抽气问题
从容器内抽气的过程中,容器内的气体质量不断减小,这属于变质量问题。分析时,将每次抽气过程中抽出的气体和剩余气体作为研究对象,质量不变,故抽气过程可看作是等温膨胀过程。
(3)分装问题
将一个大容器里的气体分装到多个小容器中的问题也是一个典型的变质量问题。分析这类问题时,可以把大容器中的气体和多个小容器中的气体看作整体研究,可将变质量问题转化为定质量问题,运用相关规律求解。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 分子动理论与气体实验定律
- 第1节 分子动理论的基本观点
- 第2节 科学测量:用油膜法估测油酸分子的大小
- 第3节 气体分子速率分布的统计规律
- 第4节 科学探究:气体压强与体积的关系
- 第5节 气体实验定律
- 第2章 固体与液体
- 第1节 固体类型及微观结构
- 第2节 表面张力和毛细现象
- 第3节 材料及其应用
- 第3章 热力学定律
- 第1节 热力学第一定律
- 第2节 能量的转化与守恒
- 第3节 热力学第二定律
- 第4节 熵——系统无序程度的量度
- 第4章 原子结构
- 第1节 电子的发现与汤姆孙原子模型
- 第2节 原子的核式结构模型
- 第3节 光谱与氢原子光谱
- 第4节 玻尔原子模型
- 第5章 原子核与核能
- 第1节 认识原子核
- 第2节 原子核衰变及半衰期
- 第3节 核力与核能
- 第4节 核裂变和核聚变
- 第5节 核能的利用与环境保护
- 第6章 波粒二象性
- 第1节 光电效应及其解释
- 第2节 实物粒子的波粒二象性
