3.3 幂函数 课件(共17张PPT)
文档属性
| 名称 | 3.3 幂函数 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-09 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
3.3 幂函数
探究:观察几个实例得出的函数解析式,有什么共同特征?
(1)如果张红购买了每千克1元的蔬菜千克,那么需要支付的费用________.
(2)如果正方形的边长为,那么正方形的面积________.
(3)如果立方体的边长为,那么立方体的体积________.
(4)如果一个正方形场地的面积为,那么这个正方形的边长
(5)如果某人秒内汽车行进了,那么他骑车的平均速度
幂函数的定义
思考:如何判断一个函数是否为幂函数?
(1)底数只能是自变量;
(2)指数是常数,且;
(3)的系数为1;
(4)项数只有一项。
例题 下列几个函数中为幂函数的是______.
①; ②;
③; ④
⑤ ⑥
⑦ 3x ; ⑧
②⑥
题型一:根据函数是幂函数求参数
例1:若幂函数 y= f(x) 的图象过点(2,),则函数的解析式为___ _ .
例2:已知y=(m2+2m-2) +2n-3是幂函数,求m,n的值.
解:解得
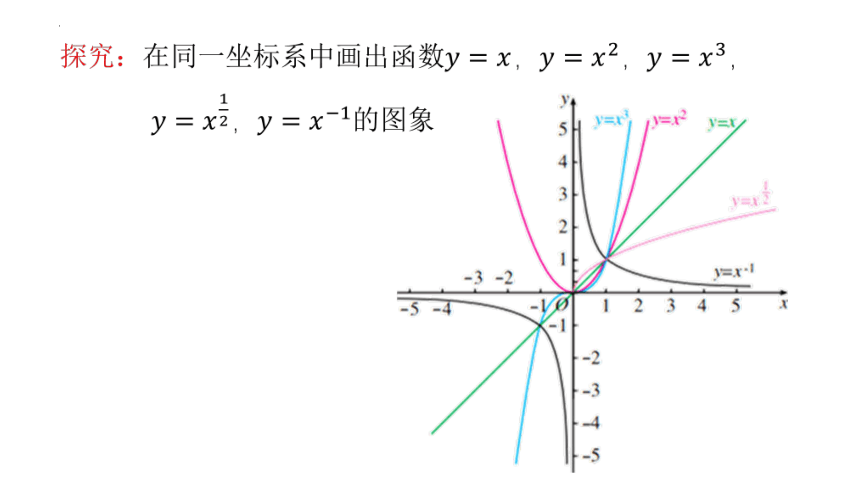
探究:在同一坐标系中画出函数,,,
,的图象
观察函数图象并结合函数解析式,将你发现的结论写在表格内.
项目
定义域
值域
奇偶性
单调性
观察幂函数图象,总结幂函数的性质
幂函数的图象一定会在第一象限,一定不在第四象限;
1、这些函数图象位置有何特征?
恒过定点(1,1)
2、这些函数有公共点吗?
【当时,还会过(0,0)】
3、在第一象限,单调性
4、奇偶性
题型二:幂函数的图象与应用
A
例题:
在区间上,指大图低
在区间上,指大图高
B
变式:
变式:若四个幂函数图象在同一坐标系中的图象如图所示,则的大小关系是( ).
B
变式:若幂函数与在第一象限内的图象如图所示,
则( )
A.
B.
C.
D.
B
例4 证明幂函数在上是增函数.
题型三:幂函数图象过定点(1,1)
变式:
题型四:幂函数的单调性与奇偶性
B
-2
变式:
例:
例:
题型五:利用幂函数单调性比较大小
比较大小:与; (2) 与.
解:(1)∵幂函数在上是单调递增,
又,∴>.
(2)∵幂函数在上单调递减,
又,∴
(3)∵幂函数和在上单调递增,
又,∴>,
∴
直接法 当幂指数相同时,可直接利用幂函数的单调性来比较
转化法 当幂指数不同时,可以先转化为相同的幂指数,再利用单调性来比较大小
中间量法 当底数不同且幂指数也不同时,不能运用单调性比较大小,可选取适当的中间值,从而达到比较大小的目的
题型六:利用幂函数单调性解不等式
变式:
例:
3.3 幂函数
探究:观察几个实例得出的函数解析式,有什么共同特征?
(1)如果张红购买了每千克1元的蔬菜千克,那么需要支付的费用________.
(2)如果正方形的边长为,那么正方形的面积________.
(3)如果立方体的边长为,那么立方体的体积________.
(4)如果一个正方形场地的面积为,那么这个正方形的边长
(5)如果某人秒内汽车行进了,那么他骑车的平均速度
幂函数的定义
思考:如何判断一个函数是否为幂函数?
(1)底数只能是自变量;
(2)指数是常数,且;
(3)的系数为1;
(4)项数只有一项。
例题 下列几个函数中为幂函数的是______.
①; ②;
③; ④
⑤ ⑥
⑦ 3x ; ⑧
②⑥
题型一:根据函数是幂函数求参数
例1:若幂函数 y= f(x) 的图象过点(2,),则函数的解析式为___ _ .
例2:已知y=(m2+2m-2) +2n-3是幂函数,求m,n的值.
解:解得
探究:在同一坐标系中画出函数,,,
,的图象
观察函数图象并结合函数解析式,将你发现的结论写在表格内.
项目
定义域
值域
奇偶性
单调性
观察幂函数图象,总结幂函数的性质
幂函数的图象一定会在第一象限,一定不在第四象限;
1、这些函数图象位置有何特征?
恒过定点(1,1)
2、这些函数有公共点吗?
【当时,还会过(0,0)】
3、在第一象限,单调性
4、奇偶性
题型二:幂函数的图象与应用
A
例题:
在区间上,指大图低
在区间上,指大图高
B
变式:
变式:若四个幂函数图象在同一坐标系中的图象如图所示,则的大小关系是( ).
B
变式:若幂函数与在第一象限内的图象如图所示,
则( )
A.
B.
C.
D.
B
例4 证明幂函数在上是增函数.
题型三:幂函数图象过定点(1,1)
变式:
题型四:幂函数的单调性与奇偶性
B
-2
变式:
例:
例:
题型五:利用幂函数单调性比较大小
比较大小:与; (2) 与.
解:(1)∵幂函数在上是单调递增,
又,∴>.
(2)∵幂函数在上单调递减,
又,∴
(3)∵幂函数和在上单调递增,
又,∴>,
∴
直接法 当幂指数相同时,可直接利用幂函数的单调性来比较
转化法 当幂指数不同时,可以先转化为相同的幂指数,再利用单调性来比较大小
中间量法 当底数不同且幂指数也不同时,不能运用单调性比较大小,可选取适当的中间值,从而达到比较大小的目的
题型六:利用幂函数单调性解不等式
变式:
例:
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
