不等式的性质2
图片预览




文档简介
课件10张PPT。9.1.2 不等式的性质(二)复习回顾 不等式的性质1 不等式的两边加(或减)同一个数(或式子),不等号的方向不变.
不等式的性质2 不等式的两边乘(或除以)同一个正数,不等号的方向不变. 不等式的性质 3 不等式的两边乘(或 除以)同一个负数,不等号的方向改变
注意: 必须把不等号的方向改变不等式的性质试一试1.若-m>5,则m -5.
2.如果 >0, 那么xy 0.
3.如果a>-1,那么a-b -1-b.
4.-0.9<-0.3,两边都除以(-0.3),得_______.
>><3 >1 用炸药爆破时,如果导火索燃烧的速度是0.8 cm/s,人跑开的速度是每秒4 m,为了使点导火索的战士在爆破时能够跑到100 m以外的安全区域,这个导火索的长度应大于多少厘米?探究解:设导火索的长度是x cm .根据题意,得
×4≥100.
答:导火索的长度应大于20 cm.
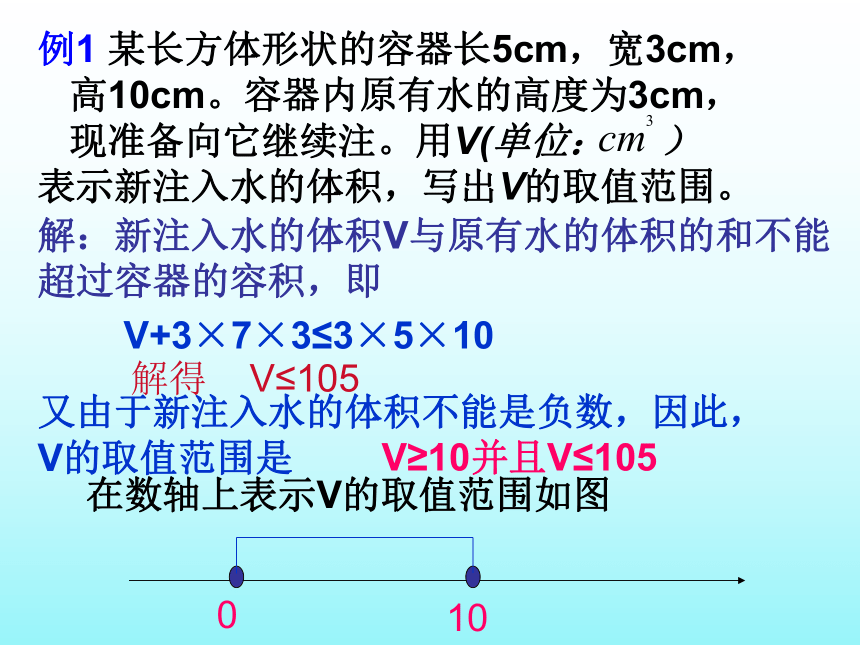
解得: x≥20例1 某长方体形状的容器长5cm,宽3cm,
高10cm。容器内原有水的高度为3cm,
现准备向它继续注。用V(单位: )
表示新注入水的体积,写出V的取值范围。
解:新注入水的体积V与原有水的体积的和不能
超过容器的容积,即V+3×7×3≤3×5×10解得 V≤105又由于新注入水的体积不能是负数,因此,
V的取值范围是V≥10并且V≤105在数轴上表示V的取值范围如图0105例2 三角形中任意两边之差
与第三边有怎样的大小关系?想一想三角形中任意两边之差小于第三边解:如图,设a,b,c为任意一个三角
形的三条边的长,则a+b>c, b+c>a, c+a>b.由式子a+b>c 移项可得a>c-b, b>c-a .类似地,由式子b+c>a及c+a>b移项可得c>a-b, b>a-c 及 c>b-a, a>b-c例3 一件由黄金与白 银制成的首饰重ag,商家
称其中黄金含量不低于90﹪,黄金与白银的密度
分别是19.3g/ 与10.5g/ ,列出不等式
表示这件首饰的体积应满足什么条件.
(质量=密度×体积)练一练:P127 练习 2本节课你的收获是什么? ※利用不等式的性质解不等式 ※不等式性质的运用
作业:P128--129
8、9、10、11、13
不抄题目
不等式的性质2 不等式的两边乘(或除以)同一个正数,不等号的方向不变. 不等式的性质 3 不等式的两边乘(或 除以)同一个负数,不等号的方向改变
注意: 必须把不等号的方向改变不等式的性质试一试1.若-m>5,则m -5.
2.如果 >0, 那么xy 0.
3.如果a>-1,那么a-b -1-b.
4.-0.9<-0.3,两边都除以(-0.3),得_______.
>><3 >1 用炸药爆破时,如果导火索燃烧的速度是0.8 cm/s,人跑开的速度是每秒4 m,为了使点导火索的战士在爆破时能够跑到100 m以外的安全区域,这个导火索的长度应大于多少厘米?探究解:设导火索的长度是x cm .根据题意,得
×4≥100.
答:导火索的长度应大于20 cm.
解得: x≥20例1 某长方体形状的容器长5cm,宽3cm,
高10cm。容器内原有水的高度为3cm,
现准备向它继续注。用V(单位: )
表示新注入水的体积,写出V的取值范围。
解:新注入水的体积V与原有水的体积的和不能
超过容器的容积,即V+3×7×3≤3×5×10解得 V≤105又由于新注入水的体积不能是负数,因此,
V的取值范围是V≥10并且V≤105在数轴上表示V的取值范围如图0105例2 三角形中任意两边之差
与第三边有怎样的大小关系?想一想三角形中任意两边之差小于第三边解:如图,设a,b,c为任意一个三角
形的三条边的长,则a+b>c, b+c>a, c+a>b.由式子a+b>c 移项可得a>c-b, b>c-a .类似地,由式子b+c>a及c+a>b移项可得c>a-b, b>a-c 及 c>b-a, a>b-c例3 一件由黄金与白 银制成的首饰重ag,商家
称其中黄金含量不低于90﹪,黄金与白银的密度
分别是19.3g/ 与10.5g/ ,列出不等式
表示这件首饰的体积应满足什么条件.
(质量=密度×体积)练一练:P127 练习 2本节课你的收获是什么? ※利用不等式的性质解不等式 ※不等式性质的运用
作业:P128--129
8、9、10、11、13
不抄题目
