2023-2024学年苏科版数学七上期中复习专题突破 第2章 有理数 课件(共24页PPT)
文档属性
| 名称 | 2023-2024学年苏科版数学七上期中复习专题突破 第2章 有理数 课件(共24页PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 816.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-11 00:00:00 | ||
图片预览





文档简介
(共24张PPT)
第2章 有理数
1
对接课标 单元架构
2
知识梳理 整合提升
3
典题自测 迎战中考
目
录
对接课标 单元架构
1
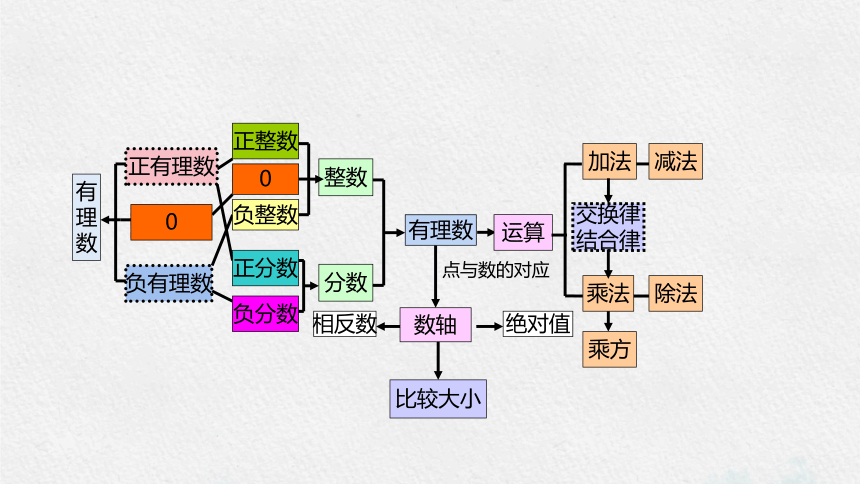
整数
分数
数轴
比较大小
相反数
绝对值
点与数的对应
负分数
正分数
正有理数
负有理数
0
有理数
0
正整数
负整数
有
理
数
减法
运算
加法
乘法
乘方
除法
交换律
结合律
有理数
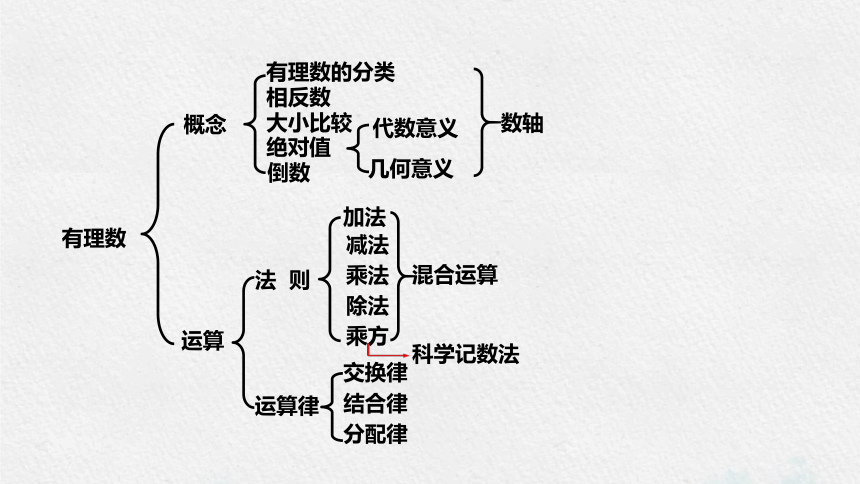
概念
运算
有理数的分类
相反数
大小比较
法 则
运算律
数轴
绝对值
倒数
加法
减法
乘法
除法
乘方
混合运算
交换律
科学记数法
结合律
分配律
代数意义
几何意义
2
知识梳理 整合提升
1
正数和负数的定义
像1,2,3,1.8%这样大于0的数叫做正数.
像-3,-1,-2,-2.7%这样在正数前面加上符号“-”(负)的数叫做负数.
有时,我们为了明确表达意义,在正数前面也加上“+”(正)号,如+3,+1.8%,+0.5,….不过一般情况下我们省略“+”不写.
注意
2
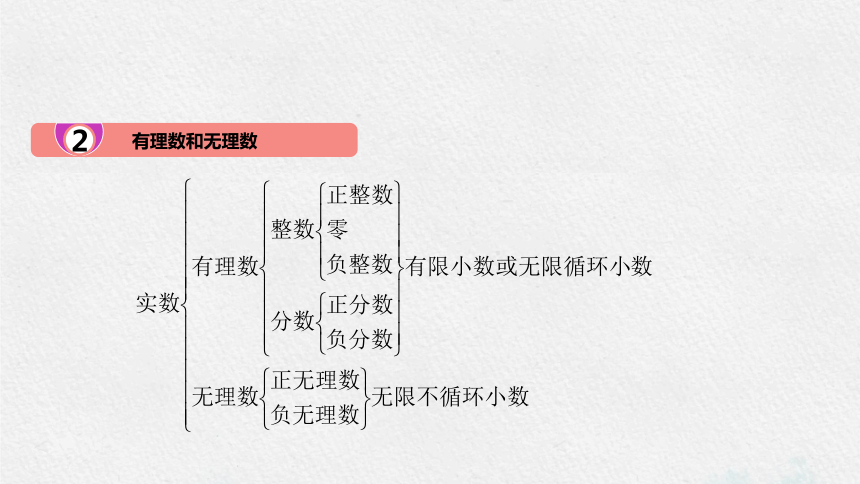
有理数和无理数
3
数轴
0
-3 -2 -1 1 2 3
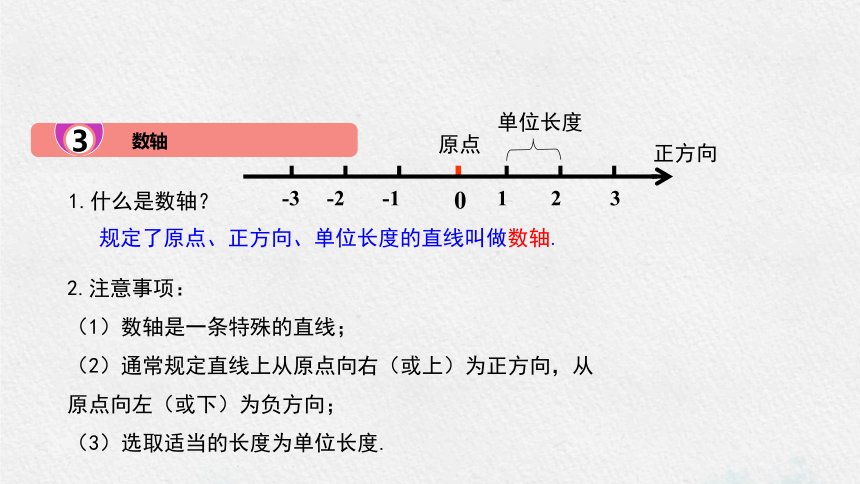
1.什么是数轴?
原点
正方向
单位长度
规定了原点、正方向、单位长度的直线叫做数轴.
2.注意事项:
(1)数轴是一条特殊的直线;
(2)通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向;
(3)选取适当的长度为单位长度.
4
绝对值和相反数
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
│-5│=5
│4│=4
4到原点的距离是4,所以4的绝对值是4,记做|4|=4
-5到原点的距离是5,所以-5的绝对值是5,记做|-5|=5
我们把一个数在数轴上对应的点到原点的距离叫做这个数的绝对值,用“| |”表示.
0到原点的距离是0,所以0的绝对值是0,记做|0|=0
4
绝对值和相反数
像3.5和-3.5这样,只有符号不同的两个数叫做互为相反数.
例如,-8的相反数是8,7的相反数是-7.
一般地,a和-a互为相反数;特别地,0的相反数是0.
5
有理数的加法和减法
有理数加法法则
(1)同号两数相加,结果取相同符号,并把绝对值相加.
(2)异号两数相加,结果取绝对值较大的加数的符号,并将较大的绝对值减较小的绝对值.互为相反数的两个数相加得0.
(3)一个数同0相加,仍得这个数.
5
有理数的加法和减法
1.有理数的减法法则:
减去一个数,等于加上这个数的相反数.
即 a -b = a +(-b)
2.有理数的减法法则是一个转化法则,减号转化为加号,同时要注意减数变为它的相反数,这样就可以用加法来解决减法问题
6
有理数的乘除
两数相乘,同号得正,异号得负,并把绝对值相乘.任何数同0相乘,都得0.
2.几个不是零的数相乘,负因数的个数为
奇数时积为负数
偶数时积为正数
3.几个数相乘若有因数为零则积为零.
4.有理数乘法的求解步骤:
有理数相乘,先确定积的符号,再确定积的绝对值.
5.乘积是1的两个数互为倒数.
1.有理数乘法法则:
6
有理数的乘除
一、有理数除法法则:
2.两数相除,同号得正,异号得负,并把绝对值相除.
0除以任何一个不等于0的数,都得0
二、有理数除法化为有理数乘法以后,可以利用有理数乘法的运算律简化运算
三、乘除混合运算往往先将除法化为乘法,然后确定积的符号,最后求出结果(乘除混合运算按从左到右的顺序进行计算)
1.
7
有理数的乘方
1.求几个相同因数的积的运算,叫做乘方.
2.乘方的符号法则:
(1)正数的任何次幂都是正数
(2)负数的奇次幂是负数,负数的偶次幂是正数
(3)零的正整数次幂都是零
3.注意:
二者的区别及相互关系;
的区别.
幂
指数
底数
8
有理数的混合运算
做有理数的混合运算时,应注意以下运算顺序
1.先乘方,再乘除,最后加减;
2.同级运算,从左到右进行;
3.如有括号,先做括号内的运算,按小括号、
中括号、大括号依次进行.
3
典题自测 迎战中考
1、某项科学研究以45分钟为1个单位时间,并将每天上午10时记为0,如9:15记为-1,1045记为1.以此类推,上午7:45记为( )
A. -7.45 B. -135 C. -2.15 D. -3
根据题意,可知基准时间为上午10时,10时以前记为负,10时以后记为正.因为7:45<10∶00,所以7∶45应该记为负数.又因为7∶45比基准时间上午10时少2小时15分钟=135分钟,135÷45=3(个)单位时间,所以上午7:45记为-3.
解析∶
解答这类题时,一般先判断题中所给的正数或负数所表示的意义,然后比较需表示的数与基准量的大小,进而得出所表示的数的正负,最后计算出需表示的数与基准量的差的绝对值,进而得出答案.
非常点评:
D
因为2是正数,一个正数的绝对值是它本身,所以2的绝对值是2.
2、2的绝对值是( )
A. -2 B. C. 2 D.
解析∶
C
本题与教材P28习题2.4第1题对应,都属于考查绝对值概念的基础题.解答本题时,还可以先在数轴上找到表示2的点,然后根据绝对值的几何意义解答.
对接教材:
3、2020的相反数是( )
A. -2020 B. 2020 C. D. -
因为只有符号不同的两个数互为相反数,与2020只有符号不同的数为-2020,所以2020的相反数是-2020.
解析∶
A
对接教材:
本题与教材P28习题2.4第2题对应,都属于考查相反数概念的基础题.求一个数的相反数时,一般使用相反数的概念求解.
4、-2的相反数是( )
A. 2 B. C. -2 D. -
因为-2=-,把- 的分子、分母颠倒后,可得- ,所以-2的倒数是- .
解析∶
D
非常点评:
本题考查倒数的概念,属于基础题. 在求一个不为0的数a的倒数时,一般先化为分数形式,然后将分子、分母颠倒.
5、写出一个负数,使这个数的绝对值小于3:_______.
解析根据题意,所写的数必须同时满足:①是负数;②绝对值小于3。据此可知这个数表示的点在数轴上的位置在表示-3和0这两个点之间(不包括0与-3),所以不妨取-1(答案不唯一).
解析∶
答案答案不唯一,如-1
非常点评:
本题考查了负数和绝对值的意义,属于基础题.解这类题目时,一般首先根据题意判断所写的数需满足的所有条件,然后据此确定这个数的范围,最后写出一个在上述范围里的数即可.
谢谢欣赏
第2章 有理数
1
对接课标 单元架构
2
知识梳理 整合提升
3
典题自测 迎战中考
目
录
对接课标 单元架构
1
整数
分数
数轴
比较大小
相反数
绝对值
点与数的对应
负分数
正分数
正有理数
负有理数
0
有理数
0
正整数
负整数
有
理
数
减法
运算
加法
乘法
乘方
除法
交换律
结合律
有理数
概念
运算
有理数的分类
相反数
大小比较
法 则
运算律
数轴
绝对值
倒数
加法
减法
乘法
除法
乘方
混合运算
交换律
科学记数法
结合律
分配律
代数意义
几何意义
2
知识梳理 整合提升
1
正数和负数的定义
像1,2,3,1.8%这样大于0的数叫做正数.
像-3,-1,-2,-2.7%这样在正数前面加上符号“-”(负)的数叫做负数.
有时,我们为了明确表达意义,在正数前面也加上“+”(正)号,如+3,+1.8%,+0.5,….不过一般情况下我们省略“+”不写.
注意
2
有理数和无理数
3
数轴
0
-3 -2 -1 1 2 3
1.什么是数轴?
原点
正方向
单位长度
规定了原点、正方向、单位长度的直线叫做数轴.
2.注意事项:
(1)数轴是一条特殊的直线;
(2)通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向;
(3)选取适当的长度为单位长度.
4
绝对值和相反数
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
│-5│=5
│4│=4
4到原点的距离是4,所以4的绝对值是4,记做|4|=4
-5到原点的距离是5,所以-5的绝对值是5,记做|-5|=5
我们把一个数在数轴上对应的点到原点的距离叫做这个数的绝对值,用“| |”表示.
0到原点的距离是0,所以0的绝对值是0,记做|0|=0
4
绝对值和相反数
像3.5和-3.5这样,只有符号不同的两个数叫做互为相反数.
例如,-8的相反数是8,7的相反数是-7.
一般地,a和-a互为相反数;特别地,0的相反数是0.
5
有理数的加法和减法
有理数加法法则
(1)同号两数相加,结果取相同符号,并把绝对值相加.
(2)异号两数相加,结果取绝对值较大的加数的符号,并将较大的绝对值减较小的绝对值.互为相反数的两个数相加得0.
(3)一个数同0相加,仍得这个数.
5
有理数的加法和减法
1.有理数的减法法则:
减去一个数,等于加上这个数的相反数.
即 a -b = a +(-b)
2.有理数的减法法则是一个转化法则,减号转化为加号,同时要注意减数变为它的相反数,这样就可以用加法来解决减法问题
6
有理数的乘除
两数相乘,同号得正,异号得负,并把绝对值相乘.任何数同0相乘,都得0.
2.几个不是零的数相乘,负因数的个数为
奇数时积为负数
偶数时积为正数
3.几个数相乘若有因数为零则积为零.
4.有理数乘法的求解步骤:
有理数相乘,先确定积的符号,再确定积的绝对值.
5.乘积是1的两个数互为倒数.
1.有理数乘法法则:
6
有理数的乘除
一、有理数除法法则:
2.两数相除,同号得正,异号得负,并把绝对值相除.
0除以任何一个不等于0的数,都得0
二、有理数除法化为有理数乘法以后,可以利用有理数乘法的运算律简化运算
三、乘除混合运算往往先将除法化为乘法,然后确定积的符号,最后求出结果(乘除混合运算按从左到右的顺序进行计算)
1.
7
有理数的乘方
1.求几个相同因数的积的运算,叫做乘方.
2.乘方的符号法则:
(1)正数的任何次幂都是正数
(2)负数的奇次幂是负数,负数的偶次幂是正数
(3)零的正整数次幂都是零
3.注意:
二者的区别及相互关系;
的区别.
幂
指数
底数
8
有理数的混合运算
做有理数的混合运算时,应注意以下运算顺序
1.先乘方,再乘除,最后加减;
2.同级运算,从左到右进行;
3.如有括号,先做括号内的运算,按小括号、
中括号、大括号依次进行.
3
典题自测 迎战中考
1、某项科学研究以45分钟为1个单位时间,并将每天上午10时记为0,如9:15记为-1,1045记为1.以此类推,上午7:45记为( )
A. -7.45 B. -135 C. -2.15 D. -3
根据题意,可知基准时间为上午10时,10时以前记为负,10时以后记为正.因为7:45<10∶00,所以7∶45应该记为负数.又因为7∶45比基准时间上午10时少2小时15分钟=135分钟,135÷45=3(个)单位时间,所以上午7:45记为-3.
解析∶
解答这类题时,一般先判断题中所给的正数或负数所表示的意义,然后比较需表示的数与基准量的大小,进而得出所表示的数的正负,最后计算出需表示的数与基准量的差的绝对值,进而得出答案.
非常点评:
D
因为2是正数,一个正数的绝对值是它本身,所以2的绝对值是2.
2、2的绝对值是( )
A. -2 B. C. 2 D.
解析∶
C
本题与教材P28习题2.4第1题对应,都属于考查绝对值概念的基础题.解答本题时,还可以先在数轴上找到表示2的点,然后根据绝对值的几何意义解答.
对接教材:
3、2020的相反数是( )
A. -2020 B. 2020 C. D. -
因为只有符号不同的两个数互为相反数,与2020只有符号不同的数为-2020,所以2020的相反数是-2020.
解析∶
A
对接教材:
本题与教材P28习题2.4第2题对应,都属于考查相反数概念的基础题.求一个数的相反数时,一般使用相反数的概念求解.
4、-2的相反数是( )
A. 2 B. C. -2 D. -
因为-2=-,把- 的分子、分母颠倒后,可得- ,所以-2的倒数是- .
解析∶
D
非常点评:
本题考查倒数的概念,属于基础题. 在求一个不为0的数a的倒数时,一般先化为分数形式,然后将分子、分母颠倒.
5、写出一个负数,使这个数的绝对值小于3:_______.
解析根据题意,所写的数必须同时满足:①是负数;②绝对值小于3。据此可知这个数表示的点在数轴上的位置在表示-3和0这两个点之间(不包括0与-3),所以不妨取-1(答案不唯一).
解析∶
答案答案不唯一,如-1
非常点评:
本题考查了负数和绝对值的意义,属于基础题.解这类题目时,一般首先根据题意判断所写的数需满足的所有条件,然后据此确定这个数的范围,最后写出一个在上述范围里的数即可.
谢谢欣赏
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
