2023-2024学年苏科版数学七上期中复习专题突破 第3章 代数式 课件(共19页PPT)
文档属性
| 名称 | 2023-2024学年苏科版数学七上期中复习专题突破 第3章 代数式 课件(共19页PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 721.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-11 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
第3章 代数式
1
对接课标 单元架构
2
知识梳理 整合提升
3
典题自测 迎战中考
目
录
对接课标 单元架构
1
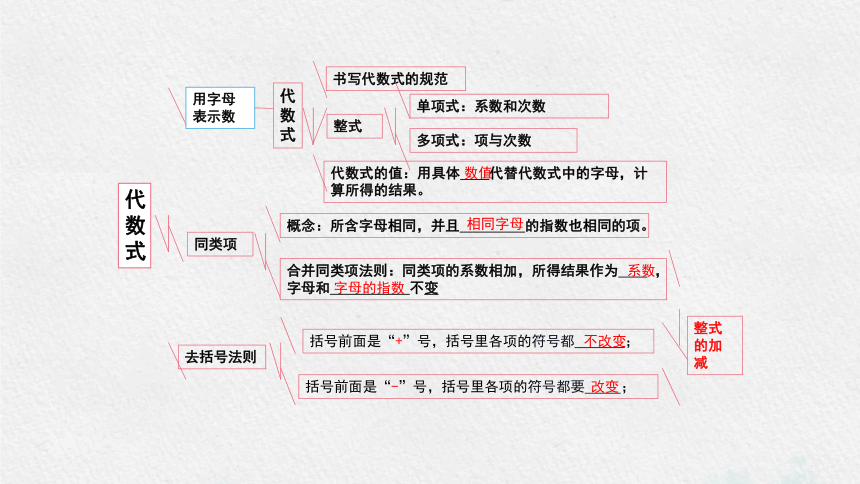
代数式
用字母表示数
代数式
书写代数式的规范
同类项
去括号法则
代数式的值:用具体 代替代数式中的字母,计算所得的结果。
概念:所含字母相同,并且 的指数也相同的项。
合并同类项法则:同类项的系数相加,所得结果作为 ,
字母和 不变
括号前面是“+”号,括号里各项的符号都 ;
括号前面是“-”号,括号里各项的符号都要 ;
整式
单项式:系数和次数
多项式:项与次数
不改变
改变
数值
相同字母
系数
字母的指数
整式的加减
2
知识梳理 整合提升
一.整式的有关概念:
1.单项式:
由数与字母的积构成的代数式叫单项式.
单独一个数或一个字母也是单项式.
与单项式有关的常识知识:
单项式中的数字因数叫做单项式的系数.
单项式中所有字母的指数的和叫做单项式的次数.
2.多项式:
几个单项式的和叫做多项式.
与多项式有关的常识知识:
多项式中的每个单项式叫做多项式的项.
多项式中次数最高项的次数,叫做这个多项式的次数.
把多项式按某字母的指数从高到低的排列叫降幂排列.
反之,叫升幂排列.
3.整式:
单项式和多项式统称为整式.
【思维点拨】整式可以有分母,但分母中不能有字母.
二.同类项以及同类项的合并:
1.同类项:
所含字母相同,并且相同字母的指数也相同的几个单项式(项)叫同类项.
2.同类项的合并:
同类项的系数相加,所得的结果作为系数,字母和字母的指数保持不变.
括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项的符号都不改变;
a+(-b+c)=a-b+c
括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项的符号都改变.
a-(-b+c)=a+b-c
简称:正不变负变
三.去括号的法则:
四、整式的加减:
整式的加减,先去括号,然后合并同类项.
3
典题自测 迎战中考
类型一:对整式的认识
下列各式:
是整式的有( )
A.5个 B.6个 C.7个 D.8个
分析:根据整式的定义,整式的分母中不能含有字母,再结合题意即可得出答案;
故答案选:C
C
类型二:对多项式的认识
下列各式:
是整式的有( )
A.5个 B.6个 C.7个 D.8个
C
分析:本题考查同类项的定义,所含字母相同且相同字母的指数也相同的项是同类项,根据同类项的定义中相同字母的指数也相同,即可判断.
解:A、相同字母的指数不同,则不是同类项,选项错误;
B、所含字母不同,则不是同类项,选项错误;
C、正确;
D、所含字母不同,则不是同类项,选项错误.
故选:C
类型三:同类项的合并
下列各式合并同类项后,结果正确的是( )
A.3a+2b=5ab B.3x3y2-2x2y=xy
C.3x2+2x3=5x5 D.4x2y-7yx2=-3x2y
分析:直接利用合并同类项法则计算得出答案.
解:A、3a+2b,无法合并,故此选项错误;
B、3x3y2-2x2y,无法合并,故此选项错误;
C、3x2+2x3,无法合并,故此选项错误;
D、4x2y-7yx2=-3x2y,正确.
故选:D.
D
类型四:整式的加减计算
计算
(1)(a-3b)-(3a-b);
(2)-3ab-2[(2a2-3ab+b)-3(a2-b)].
解:(1)原式=a-3b-3a+b=-2a-2b;
(2)原式=-3ab-2(2a2-3ab+b-3a2+3b)
=-3ab-4a2+6ab-2b+6a2-6b
=3ab+2a2-8b.
分析:先去括号,然后合并同类项即可.
类型五:求代数式以及求代数式的值
已知A=x2-2xy,B=y2+3xy.
(1)求2A-3B?
(2)若A-B+C=0,试求C?
(3)若x=-2,y=-3时,求2A-B+C的值?
解:(1)∵A=x2-2xy,B=y2+3xy,
∴2A-3B
=2(x2-2xy)-3(y2+3xy)
=2x2-4xy-3y2-9xy
=2x2-13xy-3y2;
分析:(1)直接把A=x2-2xy,B=y2+3xy代入进行计算即可;
(2)根据题意得出C的表达式,再去括号,合并同类项即可;
分析:(3)把A、B、C的表达式代入,合并同类项后,把x=-2,y=-3代入进行计算即可
解(3)∵A=x2-2xy,B=y2+3xy,C=y2+5xy-x2,
∴2A-B+C
=2(x2-2xy)-(y2+3xy)+(y2+5xy-x2)
=2x2-4xy-y2-3xy+y2+5xy-x2
=x2-2xy,
当x=-2,y=-3,原式=4-2×6=-8
解(2)∵A-B+C=0,
∴C=B-A
=(y2+3xy)-(x2-2xy)
=y2+3xy-x2+2xy
=y2+5xy-x2
类型六:根据错解求正确的代数式
李可同学欲将一个多项式加上2xy-3yz+4时,由于错把“加上”当作“减去”使得计算结果为-6xy+8yz-9,请你求出正确的答案.
分析:用这个多项式加上-6xy+8yz-9,求出这个多项式的式子,然后用这个多项式再减去-6xy+8yz-9,求出结果即可.
解:-6xy+8yz-9+2(2xy-3yz+4)
=-6xy+8yz-9+4xy-6yz+8
=-2xy+2yz-1
谢谢欣赏
第3章 代数式
1
对接课标 单元架构
2
知识梳理 整合提升
3
典题自测 迎战中考
目
录
对接课标 单元架构
1
代数式
用字母表示数
代数式
书写代数式的规范
同类项
去括号法则
代数式的值:用具体 代替代数式中的字母,计算所得的结果。
概念:所含字母相同,并且 的指数也相同的项。
合并同类项法则:同类项的系数相加,所得结果作为 ,
字母和 不变
括号前面是“+”号,括号里各项的符号都 ;
括号前面是“-”号,括号里各项的符号都要 ;
整式
单项式:系数和次数
多项式:项与次数
不改变
改变
数值
相同字母
系数
字母的指数
整式的加减
2
知识梳理 整合提升
一.整式的有关概念:
1.单项式:
由数与字母的积构成的代数式叫单项式.
单独一个数或一个字母也是单项式.
与单项式有关的常识知识:
单项式中的数字因数叫做单项式的系数.
单项式中所有字母的指数的和叫做单项式的次数.
2.多项式:
几个单项式的和叫做多项式.
与多项式有关的常识知识:
多项式中的每个单项式叫做多项式的项.
多项式中次数最高项的次数,叫做这个多项式的次数.
把多项式按某字母的指数从高到低的排列叫降幂排列.
反之,叫升幂排列.
3.整式:
单项式和多项式统称为整式.
【思维点拨】整式可以有分母,但分母中不能有字母.
二.同类项以及同类项的合并:
1.同类项:
所含字母相同,并且相同字母的指数也相同的几个单项式(项)叫同类项.
2.同类项的合并:
同类项的系数相加,所得的结果作为系数,字母和字母的指数保持不变.
括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项的符号都不改变;
a+(-b+c)=a-b+c
括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项的符号都改变.
a-(-b+c)=a+b-c
简称:正不变负变
三.去括号的法则:
四、整式的加减:
整式的加减,先去括号,然后合并同类项.
3
典题自测 迎战中考
类型一:对整式的认识
下列各式:
是整式的有( )
A.5个 B.6个 C.7个 D.8个
分析:根据整式的定义,整式的分母中不能含有字母,再结合题意即可得出答案;
故答案选:C
C
类型二:对多项式的认识
下列各式:
是整式的有( )
A.5个 B.6个 C.7个 D.8个
C
分析:本题考查同类项的定义,所含字母相同且相同字母的指数也相同的项是同类项,根据同类项的定义中相同字母的指数也相同,即可判断.
解:A、相同字母的指数不同,则不是同类项,选项错误;
B、所含字母不同,则不是同类项,选项错误;
C、正确;
D、所含字母不同,则不是同类项,选项错误.
故选:C
类型三:同类项的合并
下列各式合并同类项后,结果正确的是( )
A.3a+2b=5ab B.3x3y2-2x2y=xy
C.3x2+2x3=5x5 D.4x2y-7yx2=-3x2y
分析:直接利用合并同类项法则计算得出答案.
解:A、3a+2b,无法合并,故此选项错误;
B、3x3y2-2x2y,无法合并,故此选项错误;
C、3x2+2x3,无法合并,故此选项错误;
D、4x2y-7yx2=-3x2y,正确.
故选:D.
D
类型四:整式的加减计算
计算
(1)(a-3b)-(3a-b);
(2)-3ab-2[(2a2-3ab+b)-3(a2-b)].
解:(1)原式=a-3b-3a+b=-2a-2b;
(2)原式=-3ab-2(2a2-3ab+b-3a2+3b)
=-3ab-4a2+6ab-2b+6a2-6b
=3ab+2a2-8b.
分析:先去括号,然后合并同类项即可.
类型五:求代数式以及求代数式的值
已知A=x2-2xy,B=y2+3xy.
(1)求2A-3B?
(2)若A-B+C=0,试求C?
(3)若x=-2,y=-3时,求2A-B+C的值?
解:(1)∵A=x2-2xy,B=y2+3xy,
∴2A-3B
=2(x2-2xy)-3(y2+3xy)
=2x2-4xy-3y2-9xy
=2x2-13xy-3y2;
分析:(1)直接把A=x2-2xy,B=y2+3xy代入进行计算即可;
(2)根据题意得出C的表达式,再去括号,合并同类项即可;
分析:(3)把A、B、C的表达式代入,合并同类项后,把x=-2,y=-3代入进行计算即可
解(3)∵A=x2-2xy,B=y2+3xy,C=y2+5xy-x2,
∴2A-B+C
=2(x2-2xy)-(y2+3xy)+(y2+5xy-x2)
=2x2-4xy-y2-3xy+y2+5xy-x2
=x2-2xy,
当x=-2,y=-3,原式=4-2×6=-8
解(2)∵A-B+C=0,
∴C=B-A
=(y2+3xy)-(x2-2xy)
=y2+3xy-x2+2xy
=y2+5xy-x2
类型六:根据错解求正确的代数式
李可同学欲将一个多项式加上2xy-3yz+4时,由于错把“加上”当作“减去”使得计算结果为-6xy+8yz-9,请你求出正确的答案.
分析:用这个多项式加上-6xy+8yz-9,求出这个多项式的式子,然后用这个多项式再减去-6xy+8yz-9,求出结果即可.
解:-6xy+8yz-9+2(2xy-3yz+4)
=-6xy+8yz-9+4xy-6yz+8
=-2xy+2yz-1
谢谢欣赏
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
