探索三角形全等的条件练习题

探索三角形全等的条件练习题
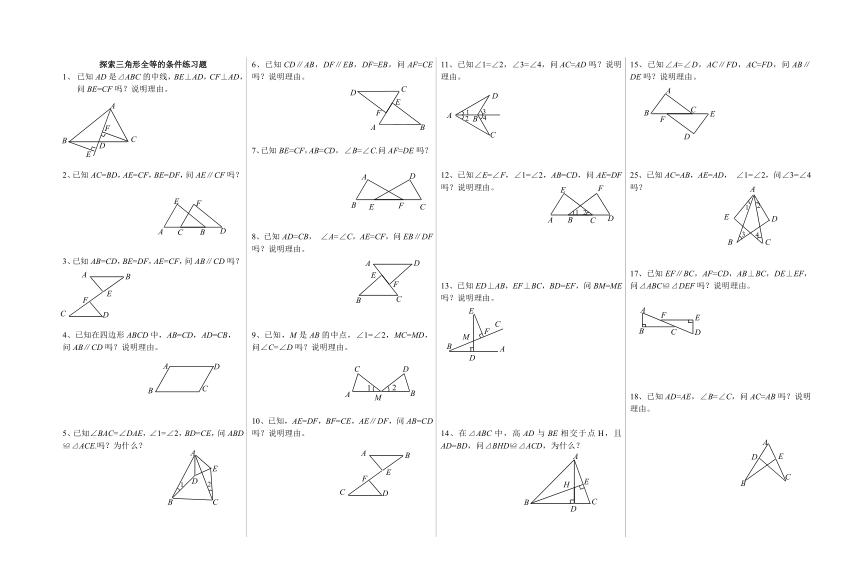
1、 已知AD是⊿ABC的中线，BE⊥AD，CF⊥AD，问BE=CF吗？说明理由。
2、已知AC=BD，AE=CF，BE=DF，问AE∥CF吗？
3、已知AB=CD，BE=DF，AE=CF，问AB∥CD吗？
4、已知在四边形ABCD中，AB=CD，AD=CB，
问AB∥CD吗？说明理由。
5、已知∠BAC=∠DAE，∠1=∠2，BD=CE，问ABD≌⊿ACE.吗？为什么？
6、已知CD∥AB，DF∥EB，DF=EB，问AF=CE吗？说明理由。
7、已知BE=CF，AB=CD， ∠B=∠C.问AF=DE吗？
8、已知AD=CB， ∠A=∠C，AE=CF，问EB∥DF吗？说明理由。
9、已知，M是AB的中点，∠1=∠2，MC=MD，问∠C=∠D吗？说明理由。
10、已知，AE=DF，BF=CE，AE∥DF，问AB=CD吗？说明理由。
11、已知∠1=∠2，∠3=∠4，问AC=AD吗？说明理由。
12、已知∠E=∠F，∠1=∠2，AB=CD，问AE=DF吗？说明理由。
13、已知ED⊥AB，EF⊥BC，BD=EF，问BM=ME吗？说明理由。
14、在⊿ABC中，高AD与BE相交于点H，且AD=BD，问⊿BHD≌⊿ACD，为什么？
15、已知∠A=∠D，AC∥FD，AC=FD，问AB∥DE吗？说明理由。
25、已知AC=AB，AE=AD， ∠1=∠2，问∠3=∠4吗？
17、已知EF∥BC，AF=CD，AB⊥BC，DE⊥EF，问⊿ABC≌⊿DEF吗？说明理由。
18、已知AD=AE，∠B=∠C，问AC=AB吗？说明理由。
19、已知AD⊥BC，BD=CD，问AB=AC吗？
20、已知∠1=∠2，BC=AD，问⊿ABC≌⊿BAD吗？
21、已知AB=AC， ∠1=∠2，AD=AE，问⊿ABD≌⊿ACE.说明理由。
22、已知BE∥DF，AD∥BC，AE=CF，问⊿AFD≌⊿CEB吗？
23、已知AD=AE，BD=CE，∠1=∠2，问⊿ABD≌⊿ACE吗？
24、已知AB=AC，AD=AE，∠1=∠2，问CE=BD吗？
16、已知CE⊥AB，DF⊥AB，AC∥DB，AC=BD，问CE=DF吗？说明理由。
26、如图，AD=BC，AE=BE，问∠C=∠D吗？
27、已知∠1=∠2，AC=BD，E，F，A，B在同一直线上，问∠3=∠4吗？
28、已知DO⊥BC，OC=OA，OB=OD，问CD=AB吗？
29、已知CE=DF，AE=BF，AE⊥AD，FD⊥AD，问⊿EAB≌⊿FDC吗？
30、已知AB与CD相交于点E，EA=EC，ED=EB，问⊿AED≌⊿CEB吗？
31、已知AB=AC，D，E分别是AB，AC的中点。问BE=CD吗？说明理由。
32、已知DE=FE，FC∥AB，问AE=CE吗？
33、已知CE⊥AB，DF⊥AB，CE=DF，AE=BF，问⊿CEB≌⊿DFA吗？说明理由。
34、如图，D，E，F，B在一条直线上，AB=CD，∠B=∠D，BF=DE，问(1)AE=CF(2)AE∥CF。
35、已知，点C是AB的中点，CD∥BE，且CD=BE，问∠D=∠E吗？说明理由。
36、已知，E、F是AB上的两点，AE=BF，又AC∥DB，AC=DB，问CF=DE吗？说明理由。
37、已知，AC⊥CE，AC=CE， ∠ABC=∠DEC=900，问BD=AB+ED吗？
38、⊿ABC≌⊿A′B′C′，AD与A′D′分别是中线，问AD=A′D′吗？
C
E
B
D
A
D
E
B
C
A
E
D
C
A
B
B
A
F
E
D
C
2
1
D
C
B
A
M
B
A
E
F
C
D
C
E
F
D
A
B
2
1
B
C
E
A
D
A
C
D
B
1
2
3
4
A
B
C
D
E
F
1
2
A
B
C
E
H
D
A
C
M
E
F
B
D
A
B
C
E
F
D
C
A
E
B
F
D
B
F
E
C
D
A
2
1
C
B
E
D
A
A
B
C
E
D
F
A
D
E
B
C
A
B
C
D
A
B
C
D
O
1
2
F
E
B
D
C
A
C
E
F
D
A
B
D
F
B
E
A
C
E
D
B
C
A
C
E
F
D
A
B
A
D
B
E
C
A
B
C
D
E
1
2
A
C
D
B
E
F
G
1
2
A
D
E
B
C
1
2
3
4
A
C
D
E
B
A
E
D
C
B
O
C
D
A
E
F
B
2
1
3
4
D
C
B
A
B
A
E
F
C
D
F
E
D
B
C
A
E
F
E
D
C
B
D
A
C
B
A
D′
C′
B′
A′
D
C
B
A
1
2