对数运算基本性质
图片预览



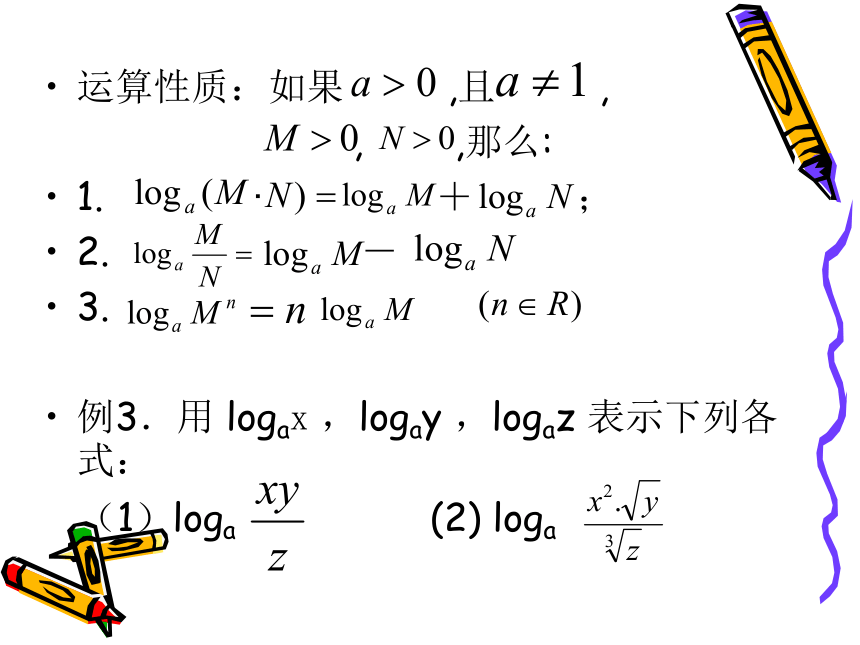

文档简介
课件11张PPT。§2.2.1对数的运算性质 复习:
1.对数的定义:
2.对数恒等式:
3.指数运算性质:(1) ·
(2) (3)
对数会有怎样的运算性质呢? 问题:根据对数的定义及指数的运算性质解答下面问题,看看你能发现什么:
设 , ,试用m,n表示 ·N), , 。
解:由题意可得 M=am , N=an
所以loga(M ·N)=loga(am · an)
=logaam+n
=m+n
即loga(M ·N) =logaM+logaN
运算性质:如果 ,且 ,
, ,那么:
1. · + ;
2. -
3.
例3.用 logax ,logay ,logaz 表示下列各式:
(1)loga (2) loga 例4.求下列各式的值:
(1)log2(47×25) (2) lg
练习:
1.用lg x , lg y ,lg z 表示下列各式:
(1)lg (xyz) (2) lg
2.求下列各式的值:
(1) log3(27×92) (2) lg 0.00001
3.已知lg2=a , lg3=b , 请用a ,b 表示 lg12 .4.求下列各式的值:
(1)log26-log23 (2) lg5+lg2
(3)log53+log5 (4)log35-log315
解(1) 法一:
原式= log2(2×3)-log23
= log22 + log23 -log23= log22 =1
法二:log26-log23 =log2 =log22 =1
(2) lg5+lg2 = lg(5×2)=lg10=1
(3)原式=log5(3× )=log51=0
(4)原式= log3 = log3 = log33-1=-15.计算lg ( 103-102)的结果。
解: lg ( 103-102)
= lg 【102( 10-1)】
= lg(102× 9)
=lg102+lg9
=2+lg9
常用对数表和自然对数表
换底公式
(a>0,且 ;c>0 ,且 ;b>0)
特别地:
P75 4. 利用对数的换底公式化简下列各式:(1)logac·logca
(2)log23·log34·log45·log52
(3)(log43+log83)(log32+log92) 解:1)logac·logca = · =1
2)log23·log34·log45·log52= · · ·
=1
3)(log43+log83)(log32+log92)
=( + )(log32 + )
= ( + )(log32+ ) = ·
=小结:本节课我们学习了对数的运算性质及换底公式,要注意指数运算性质与对数运算性质的对照。
指数运算性质: 对数运算性质:
· · +
-作业 :课本P82 3 (1)(3)(5)
4 (1)(3)
5 (1)(4)
课外练习:同步导学P57
1.对数的定义:
2.对数恒等式:
3.指数运算性质:(1) ·
(2) (3)
对数会有怎样的运算性质呢? 问题:根据对数的定义及指数的运算性质解答下面问题,看看你能发现什么:
设 , ,试用m,n表示 ·N), , 。
解:由题意可得 M=am , N=an
所以loga(M ·N)=loga(am · an)
=logaam+n
=m+n
即loga(M ·N) =logaM+logaN
运算性质:如果 ,且 ,
, ,那么:
1. · + ;
2. -
3.
例3.用 logax ,logay ,logaz 表示下列各式:
(1)loga (2) loga 例4.求下列各式的值:
(1)log2(47×25) (2) lg
练习:
1.用lg x , lg y ,lg z 表示下列各式:
(1)lg (xyz) (2) lg
2.求下列各式的值:
(1) log3(27×92) (2) lg 0.00001
3.已知lg2=a , lg3=b , 请用a ,b 表示 lg12 .4.求下列各式的值:
(1)log26-log23 (2) lg5+lg2
(3)log53+log5 (4)log35-log315
解(1) 法一:
原式= log2(2×3)-log23
= log22 + log23 -log23= log22 =1
法二:log26-log23 =log2 =log22 =1
(2) lg5+lg2 = lg(5×2)=lg10=1
(3)原式=log5(3× )=log51=0
(4)原式= log3 = log3 = log33-1=-15.计算lg ( 103-102)的结果。
解: lg ( 103-102)
= lg 【102( 10-1)】
= lg(102× 9)
=lg102+lg9
=2+lg9
常用对数表和自然对数表
换底公式
(a>0,且 ;c>0 ,且 ;b>0)
特别地:
P75 4. 利用对数的换底公式化简下列各式:(1)logac·logca
(2)log23·log34·log45·log52
(3)(log43+log83)(log32+log92) 解:1)logac·logca = · =1
2)log23·log34·log45·log52= · · ·
=1
3)(log43+log83)(log32+log92)
=( + )(log32 + )
= ( + )(log32+ ) = ·
=小结:本节课我们学习了对数的运算性质及换底公式,要注意指数运算性质与对数运算性质的对照。
指数运算性质: 对数运算性质:
· · +
-作业 :课本P82 3 (1)(3)(5)
4 (1)(3)
5 (1)(4)
课外练习:同步导学P57
