6.2 密度-2023-2024学年八年级物理上册同步高效助教课件(人教版)30页ppt
文档属性
| 名称 | 6.2 密度-2023-2024学年八年级物理上册同步高效助教课件(人教版)30页ppt |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-11-10 00:29:54 | ||
图片预览











文档简介
第2节
第六章
密 度
第1课时
国王交给金匠一定质量的黄金,打造一顶纯金的王冠,当精美无比的王冠打造完毕时,国王却怀疑金匠用其它便宜的金属来替换了黄金。于是,令人用秤去称,结果王冠的质量与交给金匠的黄金的质量是相同的。
国王还应该测出什么物理量,用什么方法才能最终判断国王是否被骗?
1.根据______不同的特性来比较。
2.控制体积相同来比较______。
颜色
质量
铜块 铁块 铝块
托盘天平
结论:体积相同的不同物质质量不同。
3.控制质量相同来比较______。
体积
4.质量和体积均不同时,可利用________________来鉴别。
单位体积的质量
结论:质量相同的不同物质体积不同。
不同体积的铝块
托盘天平
砝码
刻度尺
物质
m / g
V / cm3
/g˙cm-3
铁块1
15.8
2
铁块2
31.6
4
铁块3
47.4
6
铁块4
63.2
8
铁块5
79
10
铝块1
5.4
2
铝块2
10.8
4
铝块3
16.2
6
铝块4
21.6
8
铝块5
27
10
获取实验数据
运用图象寻找规律
补充m=0,V=0的点
为避免偶然性,应再选用其它物质进行探究。
7.9
7.9
7.9
7.9
2.7
2.7
2.7
2.7
2.7
7.9
铝
铁
铜
1.同种物质的质量与体积
成_____比,即比值是_______的;
2.不同物质的质量与体积的比值一般______。
结论:
正
不同
一定
3.物质的质量与体积的比值反映了物质的_______。
特性
1.定义:某种物质组成物体的质量与它的体积之比。
2.公式:
3.单位:
(3)单位换算: 103 kg/m3 = 1 g/cm 3
=1kg ∕ dm3=1t ∕ m3
(1)国际单位:千克每立方米(kg/m3或 kg·m-3 )
(2)常用单位:克每立方厘米(g/cm3 或 g·cm-3 )
(4)密度单位由质量单位和体积单位组成,是复合单位。
????=????????
?
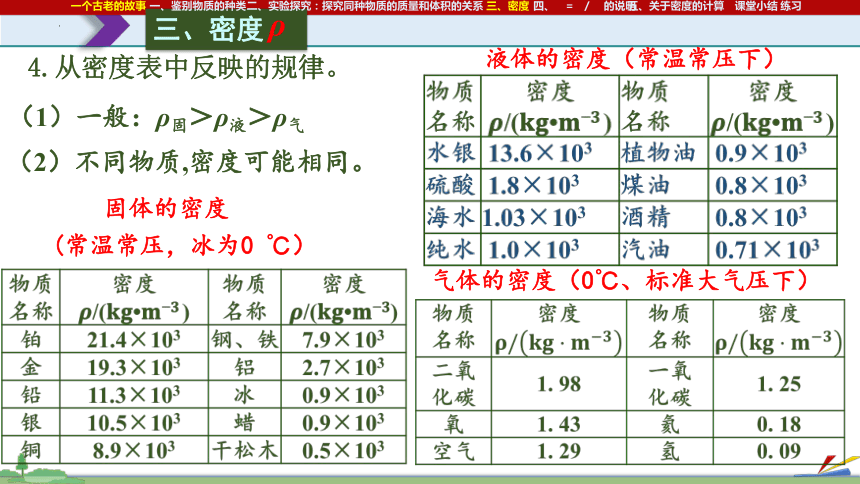
4.从密度表中反映的规律。
固体的密度
液体的密度(常温常压下)
气体的密度(0℃、标准大气压下)
(常温常压,冰为0 ℃)
(1)一般:ρ固>ρ液>ρ气
(2)不同物质,密度可能相同。
4.从密度表中反映的规律。
三.密度
液体的密度(常温常压下)
气体的密度(0℃、标准大气压下)
(1)一般:ρ固>ρ液>ρ气
(2)不同物质,密度可能相同。
(3)物态不同,密度可能不同。
(4)固体和液体密度的数值都
表示为“×103 ”的形式。
4.从密度表中反映的规律。
如ρ水=1.0×103 kg/m3 表示:
1 m3的水的质量为1.0×103 kg
(1)一般:ρ固>ρ液>ρ气
(2)不同物质,密度可能相同。
(3)物态不同,密度可能不同。
5.密度是物质的特性。
⑴一定状态下同种物质,密度不随质量和体积变化。
⑵不同种物质,密度一般不同。
⑶密度与物质的种类、物态和温度有关,与质量和体积无关。
对于密度公式????=????????的正确理解为( )
A.某种物质的密度 ρ 跟其质量 m 成正比
B.某种物质的质量 m 跟其体积 V 成反比
C.某种物质的密度 ρ 跟其体积 V 成反比
D.密度是物质的一种特性,与其质量、体积无关
?
D
例
题
第2节
翔雁物理
第六章
密 度
第2课时
1.单位统一:
2.推导式:
3.对应性:ρ、m、V对应于同一物体。
5.混合物的密度:
4.密度在数值上等于质量与体积之比;等于物体单位体积的质量。
(1)国际单位:
m ( kg ); V ( m3 ); ρ ( kg / m3 )
(2)常用单位:
m ( g ); V ( cm3 ); ρ ( g / cm3 )
密度为ρ1 、 ρ2的两种金属等质量制成合金块后的密度ρ合金1=_______;
等体积制成合金块后的密度ρ合金1=_______。
1.一块金属块的质量是1.97 t,体积是0.25 m3,它的密度多大?这可能是什么金属?
查表可知:此金属可能为铁块。
解:
1.97 t=1 970 kg
金属块的密度:
2.有一烧杯内装有质量是55 g、密度为1.1×103 kg/m3的盐水,盐水的体积是多大?
解:
V= = =50cm3
答:盐水的体积为50cm3。
由????=????????得:
?
盐水的体积:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
3.有一个质量为237 g,体积为40 cm3铁球,它是空心的吗?若是空心,则空心的体积是多大?空心中铸满铝后球的密度。
解:
237g铁的体积:
;此铁球是空心的。
空心的体积:
注入铝的质量:
球的密度:
1.空心物体的体积。
物体体积(总体积)= 材料体积(实心体积)+容积(空心体积)
2.解题方法:
(1)密度关系。
(2)质量关系。
(3)体积关系。
根据题中的文字、图或表格等信息建立某些物理量的倍数关系或比值关系,再列方程或等量代换。
1. 某型汽车使用的是237kg的钢质外壳,若替换成等体积的聚丙烯塑料材质,可减少多少质量?(ρ钢=7.9×103kg/m3,ρ塑=1.1×103kg/m3)
答案:204kg
2.一铜球,体积20cm3,质量为89g,问:
(1)此球是否空心。(2)在其空心部分铸满铝时球的总质量。
(3)铸满铝后球的平均密度。
答案:116g
密度及其应用
质量与体积的关系
定义
不同物质,质量跟体积的比值不同
同种物质,质量跟体积的比值相同
某种物质质量与体积的比叫作这种物质的密度
公式
g/cm3 和 kg/m3。它们的关系为1g/cm3 = 1×103 kg/m3
ρ =
m
V
单位
3.在容积为1.4dm3的容器内装有质量为1.3kg的石块,当向容器里灌入900g水时,水恰能充满容器,则石块的密度为多少?
答案:2.6g/cm3
4.盐水选种需要密度为1.1×103kg/m3的盐水,为了检验所配制的盐水是否符合要求,取了500ml盐水样品,称得它的质量为0.6kg,请分析,这样的盐水是否符合要求?若不符合要求,每500ml原来的盐水应加多少盐或水?
答案:500g水
5.一节车厢的容积为40m3,最大载重为30t,现要同时运输钢材和木材两种材料,使钢材和木材将车厢装满,为了能合理地利用这一车厢,试计算钢材和木材的体积应各装多少m3?(ρ钢=8×103kg/m3 ; ρ木=0.5×103kg/m3)
6.要测黄河水的含砂量,则可采取一定的河水,测出其质量和体积,根据纯水和纯砂的密度,即可算出黄河水的含砂量,黄河中上游水土流失,导致黄河水中含砂量增加,为了及时监测,现在某河段中间捞取体积为5×10-3m3的黄河水,测量其质量为5.6kg,问该河段每立方米黄河水(指纯水和砂的总体积为1m3)中的含砂量为多少㎏?(砂的密度为2.5×103kg/m3)
【答案:200kg】
7.飞机设计师为了减轻飞机自重,将一刚制零件改为铝制零件,使其质量减少了104kg,制造该零件用铝的质量是多少?(钢的密度为7.9g/cm3,铝的密度为2.7g/cm3)
【答案:54kg】
8.一空瓶的质量为200g,装满水时,瓶和水的总质量是700g,将瓶里的水倒出,在瓶内装一些金属颗粒,称出瓶和金属的总质量为878g,然后将瓶内装满水,称出瓶、水和金属总质量是1318g,求瓶内金属的密度多大?
答案:11.3g ∕ cm3
9.一个装满水的水杯,杯和水的总质量为600g,将一些金属粒倒入杯中沉底后从杯中共溢出200g水,待水溢完测得此时水杯总质量为900g,则金属粒的密度为多少?
【答案:2.5 g∕cm3】
4.已知密度分别为ρ1 、 ρ2的两种金制成合金,
(1)等质量制成时合金块的密度为ρ合金1 ________________。
(2)等体积制成时合金块的密度为ρ合金2 ________________。
(3)质量比为1∶ 3制成时合金块的密度为ρ合金3 _____________。
(用 ρ1 、 ρ2表示结果 )
第六章
密 度
第1课时
国王交给金匠一定质量的黄金,打造一顶纯金的王冠,当精美无比的王冠打造完毕时,国王却怀疑金匠用其它便宜的金属来替换了黄金。于是,令人用秤去称,结果王冠的质量与交给金匠的黄金的质量是相同的。
国王还应该测出什么物理量,用什么方法才能最终判断国王是否被骗?
1.根据______不同的特性来比较。
2.控制体积相同来比较______。
颜色
质量
铜块 铁块 铝块
托盘天平
结论:体积相同的不同物质质量不同。
3.控制质量相同来比较______。
体积
4.质量和体积均不同时,可利用________________来鉴别。
单位体积的质量
结论:质量相同的不同物质体积不同。
不同体积的铝块
托盘天平
砝码
刻度尺
物质
m / g
V / cm3
/g˙cm-3
铁块1
15.8
2
铁块2
31.6
4
铁块3
47.4
6
铁块4
63.2
8
铁块5
79
10
铝块1
5.4
2
铝块2
10.8
4
铝块3
16.2
6
铝块4
21.6
8
铝块5
27
10
获取实验数据
运用图象寻找规律
补充m=0,V=0的点
为避免偶然性,应再选用其它物质进行探究。
7.9
7.9
7.9
7.9
2.7
2.7
2.7
2.7
2.7
7.9
铝
铁
铜
1.同种物质的质量与体积
成_____比,即比值是_______的;
2.不同物质的质量与体积的比值一般______。
结论:
正
不同
一定
3.物质的质量与体积的比值反映了物质的_______。
特性
1.定义:某种物质组成物体的质量与它的体积之比。
2.公式:
3.单位:
(3)单位换算: 103 kg/m3 = 1 g/cm 3
=1kg ∕ dm3=1t ∕ m3
(1)国际单位:千克每立方米(kg/m3或 kg·m-3 )
(2)常用单位:克每立方厘米(g/cm3 或 g·cm-3 )
(4)密度单位由质量单位和体积单位组成,是复合单位。
????=????????
?
4.从密度表中反映的规律。
固体的密度
液体的密度(常温常压下)
气体的密度(0℃、标准大气压下)
(常温常压,冰为0 ℃)
(1)一般:ρ固>ρ液>ρ气
(2)不同物质,密度可能相同。
4.从密度表中反映的规律。
三.密度
液体的密度(常温常压下)
气体的密度(0℃、标准大气压下)
(1)一般:ρ固>ρ液>ρ气
(2)不同物质,密度可能相同。
(3)物态不同,密度可能不同。
(4)固体和液体密度的数值都
表示为“×103 ”的形式。
4.从密度表中反映的规律。
如ρ水=1.0×103 kg/m3 表示:
1 m3的水的质量为1.0×103 kg
(1)一般:ρ固>ρ液>ρ气
(2)不同物质,密度可能相同。
(3)物态不同,密度可能不同。
5.密度是物质的特性。
⑴一定状态下同种物质,密度不随质量和体积变化。
⑵不同种物质,密度一般不同。
⑶密度与物质的种类、物态和温度有关,与质量和体积无关。
对于密度公式????=????????的正确理解为( )
A.某种物质的密度 ρ 跟其质量 m 成正比
B.某种物质的质量 m 跟其体积 V 成反比
C.某种物质的密度 ρ 跟其体积 V 成反比
D.密度是物质的一种特性,与其质量、体积无关
?
D
例
题
第2节
翔雁物理
第六章
密 度
第2课时
1.单位统一:
2.推导式:
3.对应性:ρ、m、V对应于同一物体。
5.混合物的密度:
4.密度在数值上等于质量与体积之比;等于物体单位体积的质量。
(1)国际单位:
m ( kg ); V ( m3 ); ρ ( kg / m3 )
(2)常用单位:
m ( g ); V ( cm3 ); ρ ( g / cm3 )
密度为ρ1 、 ρ2的两种金属等质量制成合金块后的密度ρ合金1=_______;
等体积制成合金块后的密度ρ合金1=_______。
1.一块金属块的质量是1.97 t,体积是0.25 m3,它的密度多大?这可能是什么金属?
查表可知:此金属可能为铁块。
解:
1.97 t=1 970 kg
金属块的密度:
2.有一烧杯内装有质量是55 g、密度为1.1×103 kg/m3的盐水,盐水的体积是多大?
解:
V= = =50cm3
答:盐水的体积为50cm3。
由????=????????得:
?
盐水的体积:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
3.有一个质量为237 g,体积为40 cm3铁球,它是空心的吗?若是空心,则空心的体积是多大?空心中铸满铝后球的密度。
解:
237g铁的体积:
;此铁球是空心的。
空心的体积:
注入铝的质量:
球的密度:
1.空心物体的体积。
物体体积(总体积)= 材料体积(实心体积)+容积(空心体积)
2.解题方法:
(1)密度关系。
(2)质量关系。
(3)体积关系。
根据题中的文字、图或表格等信息建立某些物理量的倍数关系或比值关系,再列方程或等量代换。
1. 某型汽车使用的是237kg的钢质外壳,若替换成等体积的聚丙烯塑料材质,可减少多少质量?(ρ钢=7.9×103kg/m3,ρ塑=1.1×103kg/m3)
答案:204kg
2.一铜球,体积20cm3,质量为89g,问:
(1)此球是否空心。(2)在其空心部分铸满铝时球的总质量。
(3)铸满铝后球的平均密度。
答案:116g
密度及其应用
质量与体积的关系
定义
不同物质,质量跟体积的比值不同
同种物质,质量跟体积的比值相同
某种物质质量与体积的比叫作这种物质的密度
公式
g/cm3 和 kg/m3。它们的关系为1g/cm3 = 1×103 kg/m3
ρ =
m
V
单位
3.在容积为1.4dm3的容器内装有质量为1.3kg的石块,当向容器里灌入900g水时,水恰能充满容器,则石块的密度为多少?
答案:2.6g/cm3
4.盐水选种需要密度为1.1×103kg/m3的盐水,为了检验所配制的盐水是否符合要求,取了500ml盐水样品,称得它的质量为0.6kg,请分析,这样的盐水是否符合要求?若不符合要求,每500ml原来的盐水应加多少盐或水?
答案:500g水
5.一节车厢的容积为40m3,最大载重为30t,现要同时运输钢材和木材两种材料,使钢材和木材将车厢装满,为了能合理地利用这一车厢,试计算钢材和木材的体积应各装多少m3?(ρ钢=8×103kg/m3 ; ρ木=0.5×103kg/m3)
6.要测黄河水的含砂量,则可采取一定的河水,测出其质量和体积,根据纯水和纯砂的密度,即可算出黄河水的含砂量,黄河中上游水土流失,导致黄河水中含砂量增加,为了及时监测,现在某河段中间捞取体积为5×10-3m3的黄河水,测量其质量为5.6kg,问该河段每立方米黄河水(指纯水和砂的总体积为1m3)中的含砂量为多少㎏?(砂的密度为2.5×103kg/m3)
【答案:200kg】
7.飞机设计师为了减轻飞机自重,将一刚制零件改为铝制零件,使其质量减少了104kg,制造该零件用铝的质量是多少?(钢的密度为7.9g/cm3,铝的密度为2.7g/cm3)
【答案:54kg】
8.一空瓶的质量为200g,装满水时,瓶和水的总质量是700g,将瓶里的水倒出,在瓶内装一些金属颗粒,称出瓶和金属的总质量为878g,然后将瓶内装满水,称出瓶、水和金属总质量是1318g,求瓶内金属的密度多大?
答案:11.3g ∕ cm3
9.一个装满水的水杯,杯和水的总质量为600g,将一些金属粒倒入杯中沉底后从杯中共溢出200g水,待水溢完测得此时水杯总质量为900g,则金属粒的密度为多少?
【答案:2.5 g∕cm3】
4.已知密度分别为ρ1 、 ρ2的两种金制成合金,
(1)等质量制成时合金块的密度为ρ合金1 ________________。
(2)等体积制成时合金块的密度为ρ合金2 ________________。
(3)质量比为1∶ 3制成时合金块的密度为ρ合金3 _____________。
(用 ρ1 、 ρ2表示结果 )
同课章节目录
- 科学之旅
- 第一章 机械运动
- 第1节 长度和时间的测量
- 第2节 运动的描述
- 第3节 运动的快慢
- 第4节 测量平均速度
- 第二章 声现象
- 第1节 声音的产生和传播
- 第2节 声音的特性
- 第3节 声的利用
- 第4节 噪声的危害和控制
- 第三章 物态变化
- 第1节 温度
- 第2节 熔化和凝固
- 第3节 汽化和液化
- 第4节 升华和凝华
- 第四章 光现象
- 第1节 光的直线传播
- 第2节 光的反射
- 第3节 平面镜成像
- 第4节 光的折射
- 第5节 光的色散
- 第五章 透镜及其应用
- 第1节 透镜
- 第2节 生活中的透镜
- 第3节 凸透镜成像的规律
- 第4节 眼睛和眼镜
- 第5节 显微镜和望远镜
- 第六章 质量和密度
- 第1节 质量
- 第2节 密度
- 第3节 测量物质的密度
- 第4节 密度与社会生活
