不等式及其解集
图片预览

文档简介
课 题 9.1.1 不等式及其解集
授课人 透堡中学
时 间 2008.5.15上午第二节
地 点 连江四中五层多媒体教室 七年(2)班
教学目标 知识与技能 1、感受生活中存在着大量的不等关系,了解不等式和一元一次不等式的意义;2、通过解决简单的实际问题,使学生自发地寻找不等式的解,会把不等式的解集正确地表示到数轴上.过程与方法 经历由具体实例建立不等模型的过程,经历探究不等式解与解集的不同意义的过程,渗透数形结合思想。 情感态度与价值观通过对不等式、不等式解与解集的探究,引导学生在独立思考的基础上积极参与对数学问题的讨论,培养他们的合作交流意识;让学生充分体会到生活中处处有数学,并能将它们应用到生活的各个领域。
教学重点 正确理解不等式、 不等式解与解集的意义,把不等式的解集正确地表示到数轴上。
教学难点 正确理解不等式解集的意义。
课前准备 多媒体课件
教学过程(师生活动) 设计理念
提出问题 多媒体演示:1、小芳和她的外公、外婆正在跷跷板上做游戏.现在小芳不玩了,跷跷板发生了倾斜,游戏无法继续进行下去了.这是什么原因呢?2、某日,李老师准备在7:00从马鼻乘车到30千米之外的连江县城开会,假如该车匀速行驶且中间不停车,要在8:40之前到达县城,车速应满足什么条件?(引导学生从时间和路程上去分析) 通过实例创设情境,从“等”过渡到“不等”,培养学生的观察能力,激发他们的学习兴趣.
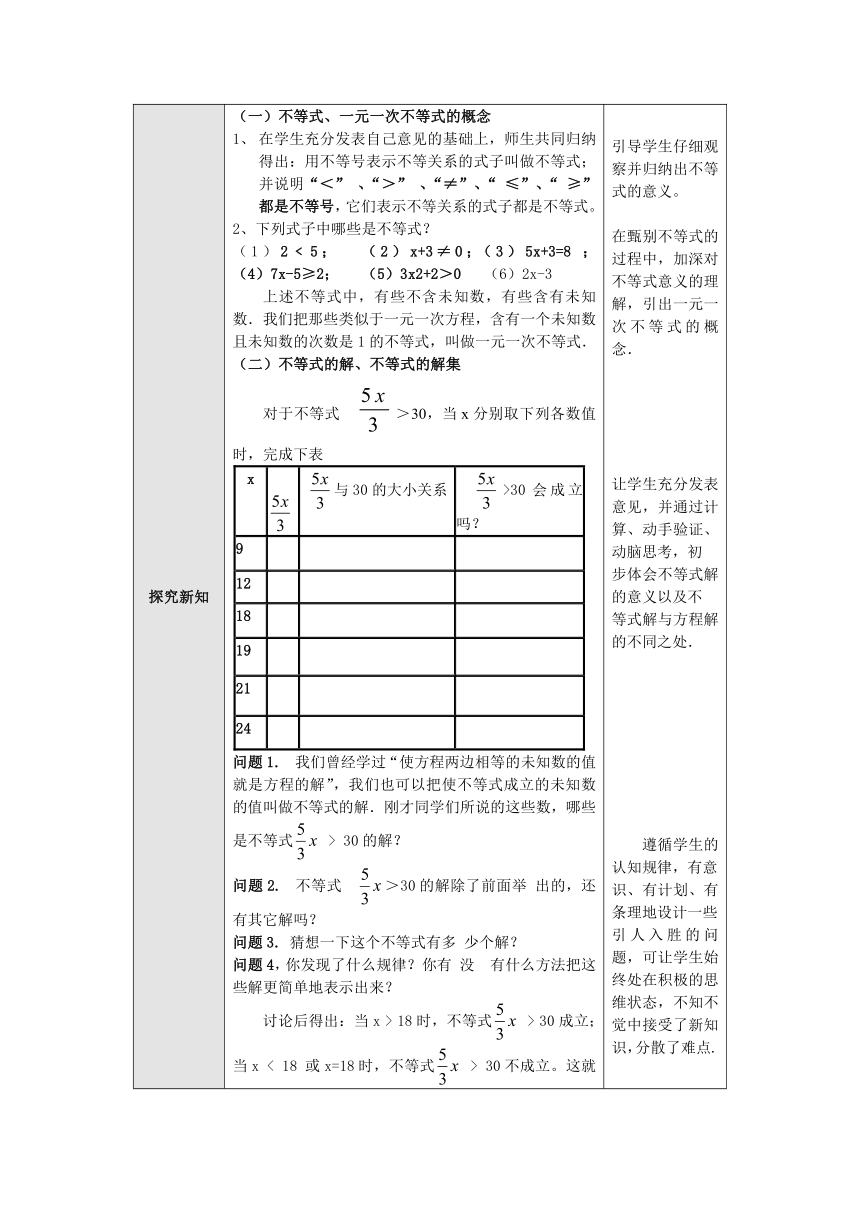
探究新知 (一)不等式、一元一次不等式的概念在学生充分发表自己意见的基础上,师生共同归纳得出:用不等号表示不等关系的式子叫做不等式;并说明“<” 、“>” 、“≠”、“ ≤”、“ ≥”都是不等号,它们表示不等关系的式子都是不等式。2、下列式子中哪些是不等式?(1)2﹤5; (2)x+3≠0;(3)5x+3=8 ; (4)7x-5≥2; (5)3x2+2>0 (6)2x-3 上述不等式中,有些不含未知数,有些含有未知数.我们把那些类似于一元一次方程,含有一个未知数且未知数的次数是1的不等式,叫做一元一次不等式.(二)不等式的解、不等式的解集 对于不等式 >30,当x分别取下列各数值时,完成下表x 与30的大小关系 >30会成立吗?9 12 18 19 21 24 问题1. 我们曾经学过“使方程两边相等的未知数的值就是方程的解”,我们也可以把使不等式成立的未知数的值叫做不等式的解.刚才同学们所说的这些数,哪些是不等式 > 30的解?问题2. 不等式 >30的解除了前面举 出的,还有其它解吗?问题3. 猜想一下这个不等式有多 少个解?问题4,你发现了什么规律?你有 没 有什么方法把这些解更简单地表示出来?讨论后得出:当x > 18时,不等式 > 30成立;当x < 18 或x=18时,不等式 > 30不成立。这就是说,任何一个大于18的数都是不等式 > 30的解,这样的解有无数个。因此,x > 18表示了能使不等式 > 30成立的“x”的取值范围。我们把它叫做不等式 > 30的解的集合,简称解集.这个解集还可以用数轴来表示(教师示范表示方法).回到前面的问题,要使汽车在18:40以前到达连江,车速必须大于每小时18千米。一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集.求不等式的解集的过程叫做解不等式. 引导学生仔细观察并归纳出不等式的意义。在甄别不等式的过程中,加深对不等式意义的理解,引出一元一次不等式的概念. 让学生充分发表意见,并通过计算、动手验证、动脑思考,初步体会不等式解的意义以及不等式解与方程解的不同之处. 遵循学生的认知规律,有意识、有计划、有条理地设计一些引人入胜的问题,可让学生始终处在积极的思维状态,不知不觉中接受了新知识,分散了难点.
巩固新知 1、下列数值哪些是不等式x+2≤5的解 它的解集是什么 并在数轴上表示解集。 -4, 3.1, 0, 1000, 2.5, 3, -2.5 , 4.8, 12, 2 2、判断下列说法是否正确:(1)、2是不等式x-3<5的解。( )(2)、-4是不等式x+4>0的解。( )(3)、不等式x+6>1的解集是x=0。( )(4)、不等式x-3<1的解有无穷多个,解集是x<4。 ( )(5)、不等式x+3<5的正整数解是1。( )(6)、x>1是不等式x+1>0的解集。( ) 巩固对不等式解集概念的理解,并会在数轴上表示不等式的解集。
小结与作业
总结归纳 1、不等式与一元一次不等式的概念;2、不等式的解与不等式的解集;3、不等式的解集在数轴上的表示. 通过总结归纳,完善学生已有的知识结构。
布置作业 1、必做题:教科书第128页习题9.1第1、2、3题其中第3题的第(1)(2)两小题的解集要在数轴上表示出来
课后反思与延伸 1、a,b两个实数在数轴上的对应点如图所示:用“<”或“>”号填空:(1)a__________b; (2)|a|__________|b|; (3)a+b__________0; (4)a-b__________0; (5)a+b__________a-b; (6)ab__________a.某开山工程正在进行爆破作业,已知导火索燃烧的速度是每秒0.8cm,人跑开的速度是每秒4m,为了使放炮的工人在爆炸时能跑到100m外的安全地带导火索的长度应超过多少cm?3、找出不等式3x-1>5的五个解,并比较它们与方程3x-1=5的解的大小。4、试写出一个不等式使它的解集满足下列条件:(1)x= - 2是不等式的一个解;(2)不等式的正整数解只有1、2;(3)不等式的解中不含 - 3. 反思与延伸为后面的课程做铺垫
课堂设计理念
本课设置了丰富的实际情境,比如跷跷板游戏等,研究这些问题,可以使学生体会到现实生活中存在着大量的不等关系,不等式是现实世界中不等关系的一种数学表示形式,它也是刻画现实世界中量与量之间关系的有效模型. 教学中要突出知识之间的内在联系.不等式与方程一样,都是反映客观事物变化规律及其关系的模型.在教学中,类比已经学过的方程知识,引导学生自己去探索、发现、甄别,从而得出一元一次不等式、不等式的解与解集的意义. 教学过程也是学生的认知过程,只有学生积极地参与教学活动才能收到良好的效果.因此,本课采用启发诱导、实例探究、讲练结合的教学方法,揭示知识的发生和形成过程.这种教学方法以“生动探索”为基础,先“引导发现”,后“讲评点拨”,让学生在克服困难与障碍的过程中充分发挥自己的观察力、想像力和思维力,再加上多媒体的运用,使学生真正成为学习的主体。
授课人 透堡中学
时 间 2008.5.15上午第二节
地 点 连江四中五层多媒体教室 七年(2)班
教学目标 知识与技能 1、感受生活中存在着大量的不等关系,了解不等式和一元一次不等式的意义;2、通过解决简单的实际问题,使学生自发地寻找不等式的解,会把不等式的解集正确地表示到数轴上.过程与方法 经历由具体实例建立不等模型的过程,经历探究不等式解与解集的不同意义的过程,渗透数形结合思想。 情感态度与价值观通过对不等式、不等式解与解集的探究,引导学生在独立思考的基础上积极参与对数学问题的讨论,培养他们的合作交流意识;让学生充分体会到生活中处处有数学,并能将它们应用到生活的各个领域。
教学重点 正确理解不等式、 不等式解与解集的意义,把不等式的解集正确地表示到数轴上。
教学难点 正确理解不等式解集的意义。
课前准备 多媒体课件
教学过程(师生活动) 设计理念
提出问题 多媒体演示:1、小芳和她的外公、外婆正在跷跷板上做游戏.现在小芳不玩了,跷跷板发生了倾斜,游戏无法继续进行下去了.这是什么原因呢?2、某日,李老师准备在7:00从马鼻乘车到30千米之外的连江县城开会,假如该车匀速行驶且中间不停车,要在8:40之前到达县城,车速应满足什么条件?(引导学生从时间和路程上去分析) 通过实例创设情境,从“等”过渡到“不等”,培养学生的观察能力,激发他们的学习兴趣.
探究新知 (一)不等式、一元一次不等式的概念在学生充分发表自己意见的基础上,师生共同归纳得出:用不等号表示不等关系的式子叫做不等式;并说明“<” 、“>” 、“≠”、“ ≤”、“ ≥”都是不等号,它们表示不等关系的式子都是不等式。2、下列式子中哪些是不等式?(1)2﹤5; (2)x+3≠0;(3)5x+3=8 ; (4)7x-5≥2; (5)3x2+2>0 (6)2x-3 上述不等式中,有些不含未知数,有些含有未知数.我们把那些类似于一元一次方程,含有一个未知数且未知数的次数是1的不等式,叫做一元一次不等式.(二)不等式的解、不等式的解集 对于不等式 >30,当x分别取下列各数值时,完成下表x 与30的大小关系 >30会成立吗?9 12 18 19 21 24 问题1. 我们曾经学过“使方程两边相等的未知数的值就是方程的解”,我们也可以把使不等式成立的未知数的值叫做不等式的解.刚才同学们所说的这些数,哪些是不等式 > 30的解?问题2. 不等式 >30的解除了前面举 出的,还有其它解吗?问题3. 猜想一下这个不等式有多 少个解?问题4,你发现了什么规律?你有 没 有什么方法把这些解更简单地表示出来?讨论后得出:当x > 18时,不等式 > 30成立;当x < 18 或x=18时,不等式 > 30不成立。这就是说,任何一个大于18的数都是不等式 > 30的解,这样的解有无数个。因此,x > 18表示了能使不等式 > 30成立的“x”的取值范围。我们把它叫做不等式 > 30的解的集合,简称解集.这个解集还可以用数轴来表示(教师示范表示方法).回到前面的问题,要使汽车在18:40以前到达连江,车速必须大于每小时18千米。一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集.求不等式的解集的过程叫做解不等式. 引导学生仔细观察并归纳出不等式的意义。在甄别不等式的过程中,加深对不等式意义的理解,引出一元一次不等式的概念. 让学生充分发表意见,并通过计算、动手验证、动脑思考,初步体会不等式解的意义以及不等式解与方程解的不同之处. 遵循学生的认知规律,有意识、有计划、有条理地设计一些引人入胜的问题,可让学生始终处在积极的思维状态,不知不觉中接受了新知识,分散了难点.
巩固新知 1、下列数值哪些是不等式x+2≤5的解 它的解集是什么 并在数轴上表示解集。 -4, 3.1, 0, 1000, 2.5, 3, -2.5 , 4.8, 12, 2 2、判断下列说法是否正确:(1)、2是不等式x-3<5的解。( )(2)、-4是不等式x+4>0的解。( )(3)、不等式x+6>1的解集是x=0。( )(4)、不等式x-3<1的解有无穷多个,解集是x<4。 ( )(5)、不等式x+3<5的正整数解是1。( )(6)、x>1是不等式x+1>0的解集。( ) 巩固对不等式解集概念的理解,并会在数轴上表示不等式的解集。
小结与作业
总结归纳 1、不等式与一元一次不等式的概念;2、不等式的解与不等式的解集;3、不等式的解集在数轴上的表示. 通过总结归纳,完善学生已有的知识结构。
布置作业 1、必做题:教科书第128页习题9.1第1、2、3题其中第3题的第(1)(2)两小题的解集要在数轴上表示出来
课后反思与延伸 1、a,b两个实数在数轴上的对应点如图所示:用“<”或“>”号填空:(1)a__________b; (2)|a|__________|b|; (3)a+b__________0; (4)a-b__________0; (5)a+b__________a-b; (6)ab__________a.某开山工程正在进行爆破作业,已知导火索燃烧的速度是每秒0.8cm,人跑开的速度是每秒4m,为了使放炮的工人在爆炸时能跑到100m外的安全地带导火索的长度应超过多少cm?3、找出不等式3x-1>5的五个解,并比较它们与方程3x-1=5的解的大小。4、试写出一个不等式使它的解集满足下列条件:(1)x= - 2是不等式的一个解;(2)不等式的正整数解只有1、2;(3)不等式的解中不含 - 3. 反思与延伸为后面的课程做铺垫
课堂设计理念
本课设置了丰富的实际情境,比如跷跷板游戏等,研究这些问题,可以使学生体会到现实生活中存在着大量的不等关系,不等式是现实世界中不等关系的一种数学表示形式,它也是刻画现实世界中量与量之间关系的有效模型. 教学中要突出知识之间的内在联系.不等式与方程一样,都是反映客观事物变化规律及其关系的模型.在教学中,类比已经学过的方程知识,引导学生自己去探索、发现、甄别,从而得出一元一次不等式、不等式的解与解集的意义. 教学过程也是学生的认知过程,只有学生积极地参与教学活动才能收到良好的效果.因此,本课采用启发诱导、实例探究、讲练结合的教学方法,揭示知识的发生和形成过程.这种教学方法以“生动探索”为基础,先“引导发现”,后“讲评点拨”,让学生在克服困难与障碍的过程中充分发挥自己的观察力、想像力和思维力,再加上多媒体的运用,使学生真正成为学习的主体。
