5.1.1 认识一元一次方程 课件(共18张PPT)-2023-2024学年七年级数学上册同步精品课件(北师大版)
文档属性
| 名称 | 5.1.1 认识一元一次方程 课件(共18张PPT)-2023-2024学年七年级数学上册同步精品课件(北师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 834.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-11 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
第五章 一元一次方程
第1节 认识一元一次方程(1)
导入新课
讲授新课
课堂小结
随堂训练
学习目标
1.理解一元一次方程的概念.
2.会根据具体问题中的等量关系列出一元一次方程.
情境引入
老师的年龄乘以3再减去7刚好为23,那现在你能知道老师的年龄吗?你是怎么猜?
小游戏:猜小明的年龄
情境引入
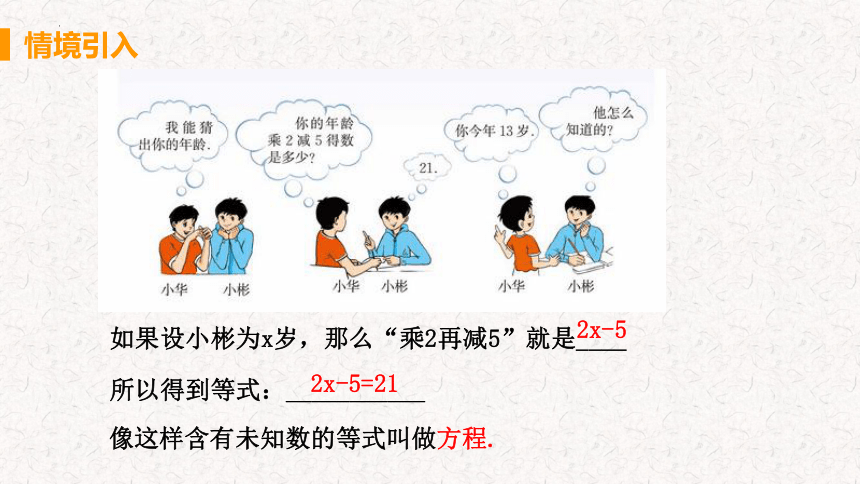
如果设小彬为x岁,那么“乘2再减5”就是____
所以得到等式:___________
2x-5=21
2x-5
像这样含有未知数的等式叫做方程.
合作探究
知识点1 一元一次方程
新课讲解
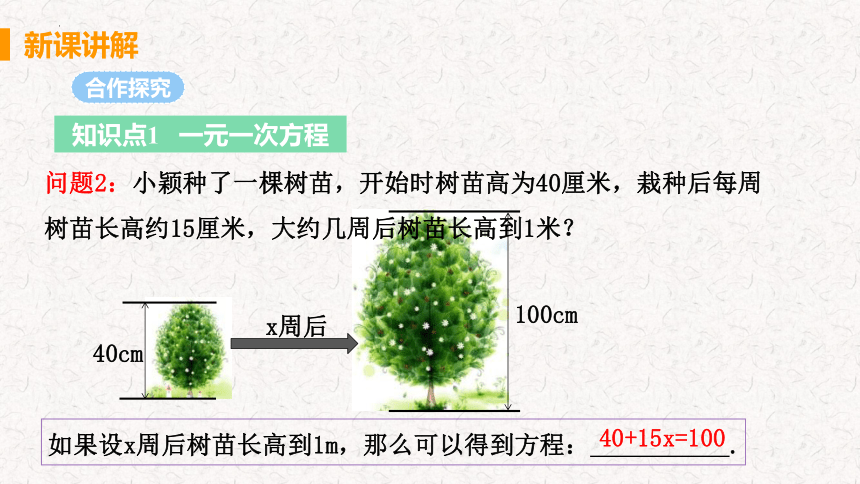
问题2:小颖种了一棵树苗,开始时树苗高为40厘米,栽种后每周树苗长高约15厘米,大约几周后树苗长高到1米?
40cm
100cm
x周后
如果设x周后树苗长高到1m,那么可以得到方程: .
40+15x=100
新课讲解
问题3:甲、乙两地相距 22 km,张叔叔从甲地出发到乙地,每时比原计划多行走 1 km,因此提前 12 min 到达乙地,张叔叔原计划每时行走多少千米?
设张叔叔原计划每时行走 x km,可以得到方程:___________.
新课讲解
问题4:第六次全国人口普查统计数据, 2010年全国每10万人中具有大学文化程度的人数为8930人,它比2000年增长了147.30%,求2000年每10万人中约有多少人具有大学文化程度
如果设2000年每10万人中约有x人具有大学文化程度,那么可以得到方程:
x(1+147.30%)=8930
新课讲解
问题5:某长方形操场的面积是 5 850 m2,长和宽之差为 25 m,这个操场的长与宽分别是多少米?
如果设这个操场的宽为 x m,那么长为(x+25)m.由此可以得到方程:_______________.
x(x+25)=5 850
新课讲解
(1)由上面的问题你得到了哪些方程?其中哪些是你熟悉的方程?与同伴进行交流.
2x – 5 = 21
40 + 5x = 100
x(1 + 147.30%) = 8 930
x(x + 25)= 5 850
议一议
新课讲解
(2)方程 2x–5=21,40+5x=100,x(1+ 147.30%)= 8 930 有什么共同点?
在一个方程中,只_______________,而且方程中的代数式都是整式,_____________都是1,这样的方程叫做一元一次方程.
含有一个未知数
未知数的指数
判断一个方程是一元一次方程,化简后必须满足三个条件:①含有一个未知数;
②未知数的指数是1;
③方程中的代数式都是整式.
新课讲解
典例分析
例1.判断下列各式是不是一元一次方程.
①2x2-5=4;②-m+8=1;③x=1;④x+y=1;
⑤x+3>0;⑥2x2-2(x2-x)=1;⑦ ;⑧πx=12.
√
√
√
√
新课讲解
典例分析
例2.若关于x的方程(m-2)xm2-2+4=7是一元一次方程,求m的值.
解:根据一元一次方程的定义可知
m2-2 =2,且m-2≠0
所以 m =-2.
使方程左、右两边的值相等的未知数的值,叫做方程的解.
x=2是方程3x+(10-x)=20的解吗?
新课讲解
在“猜年龄”游戏中,当被告知计算的结果是21时,我们所列的方程为3x-7=23,从而求出年龄是10.由于10能使方程的两边相等,我们就把10叫做3x-7=23的解.
新课讲解
典例分析
例3.检验下列各数是不是方程5x-2=7+2x的解,并写出检验过程.
(1)x=2; (2)x=3.
解:(1)将x=2代入方程,左边=8,右边=11,左边≠右边,所以x=2不是方程5x-2=7+2x的解;
(2)将x=3代入方程,左边=13,右边=13,左边=右边,所以x=3是方程5x-2=7+2x的解.
当堂小练
1.下列说法正确的是 ( )
A.含有一个未知数的等式叫一元一次方程。
B.未知数的次数是1的方程叫一元一次方程。
C.含有一个未知数,并且未知数的次数是1的整式叫一元一次方程。
D. 不是一元一次方程。
当堂小练
2. 是一元一次方程,则k =___
当堂小练
3.小刚准备用自己节省的零花钱购买一台MP4来学习英语,他已存有100元,并计划从本月起每月节省30元,直到他有460元.设x个月后小刚有460元,则可列出计算月数的方程为( )
A.30x+100=460 B.30x-100=460
C.x-100=460 D.x+150=460
课堂小结
1.在一个方程中,只含有一个未知数x(元),并且未知数的指数是1(次),这样的方程叫做一元一次方程.
2.根据题意,列方程的一般步骤:
(1)分析题意,找等量关系
(2)合理设出未知数
(3)根据等量关系,列出方程
第五章 一元一次方程
第1节 认识一元一次方程(1)
导入新课
讲授新课
课堂小结
随堂训练
学习目标
1.理解一元一次方程的概念.
2.会根据具体问题中的等量关系列出一元一次方程.
情境引入
老师的年龄乘以3再减去7刚好为23,那现在你能知道老师的年龄吗?你是怎么猜?
小游戏:猜小明的年龄
情境引入
如果设小彬为x岁,那么“乘2再减5”就是____
所以得到等式:___________
2x-5=21
2x-5
像这样含有未知数的等式叫做方程.
合作探究
知识点1 一元一次方程
新课讲解
问题2:小颖种了一棵树苗,开始时树苗高为40厘米,栽种后每周树苗长高约15厘米,大约几周后树苗长高到1米?
40cm
100cm
x周后
如果设x周后树苗长高到1m,那么可以得到方程: .
40+15x=100
新课讲解
问题3:甲、乙两地相距 22 km,张叔叔从甲地出发到乙地,每时比原计划多行走 1 km,因此提前 12 min 到达乙地,张叔叔原计划每时行走多少千米?
设张叔叔原计划每时行走 x km,可以得到方程:___________.
新课讲解
问题4:第六次全国人口普查统计数据, 2010年全国每10万人中具有大学文化程度的人数为8930人,它比2000年增长了147.30%,求2000年每10万人中约有多少人具有大学文化程度
如果设2000年每10万人中约有x人具有大学文化程度,那么可以得到方程:
x(1+147.30%)=8930
新课讲解
问题5:某长方形操场的面积是 5 850 m2,长和宽之差为 25 m,这个操场的长与宽分别是多少米?
如果设这个操场的宽为 x m,那么长为(x+25)m.由此可以得到方程:_______________.
x(x+25)=5 850
新课讲解
(1)由上面的问题你得到了哪些方程?其中哪些是你熟悉的方程?与同伴进行交流.
2x – 5 = 21
40 + 5x = 100
x(1 + 147.30%) = 8 930
x(x + 25)= 5 850
议一议
新课讲解
(2)方程 2x–5=21,40+5x=100,x(1+ 147.30%)= 8 930 有什么共同点?
在一个方程中,只_______________,而且方程中的代数式都是整式,_____________都是1,这样的方程叫做一元一次方程.
含有一个未知数
未知数的指数
判断一个方程是一元一次方程,化简后必须满足三个条件:①含有一个未知数;
②未知数的指数是1;
③方程中的代数式都是整式.
新课讲解
典例分析
例1.判断下列各式是不是一元一次方程.
①2x2-5=4;②-m+8=1;③x=1;④x+y=1;
⑤x+3>0;⑥2x2-2(x2-x)=1;⑦ ;⑧πx=12.
√
√
√
√
新课讲解
典例分析
例2.若关于x的方程(m-2)xm2-2+4=7是一元一次方程,求m的值.
解:根据一元一次方程的定义可知
m2-2 =2,且m-2≠0
所以 m =-2.
使方程左、右两边的值相等的未知数的值,叫做方程的解.
x=2是方程3x+(10-x)=20的解吗?
新课讲解
在“猜年龄”游戏中,当被告知计算的结果是21时,我们所列的方程为3x-7=23,从而求出年龄是10.由于10能使方程的两边相等,我们就把10叫做3x-7=23的解.
新课讲解
典例分析
例3.检验下列各数是不是方程5x-2=7+2x的解,并写出检验过程.
(1)x=2; (2)x=3.
解:(1)将x=2代入方程,左边=8,右边=11,左边≠右边,所以x=2不是方程5x-2=7+2x的解;
(2)将x=3代入方程,左边=13,右边=13,左边=右边,所以x=3是方程5x-2=7+2x的解.
当堂小练
1.下列说法正确的是 ( )
A.含有一个未知数的等式叫一元一次方程。
B.未知数的次数是1的方程叫一元一次方程。
C.含有一个未知数,并且未知数的次数是1的整式叫一元一次方程。
D. 不是一元一次方程。
当堂小练
2. 是一元一次方程,则k =___
当堂小练
3.小刚准备用自己节省的零花钱购买一台MP4来学习英语,他已存有100元,并计划从本月起每月节省30元,直到他有460元.设x个月后小刚有460元,则可列出计算月数的方程为( )
A.30x+100=460 B.30x-100=460
C.x-100=460 D.x+150=460
课堂小结
1.在一个方程中,只含有一个未知数x(元),并且未知数的指数是1(次),这样的方程叫做一元一次方程.
2.根据题意,列方程的一般步骤:
(1)分析题意,找等量关系
(2)合理设出未知数
(3)根据等量关系,列出方程
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
