4.4 角的比较课件(共20张PPT)-2023-2024学年七年级数学上册同步精品课件(北师大版)
文档属性
| 名称 | 4.4 角的比较课件(共20张PPT)-2023-2024学年七年级数学上册同步精品课件(北师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 616.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-11 00:00:00 | ||
图片预览





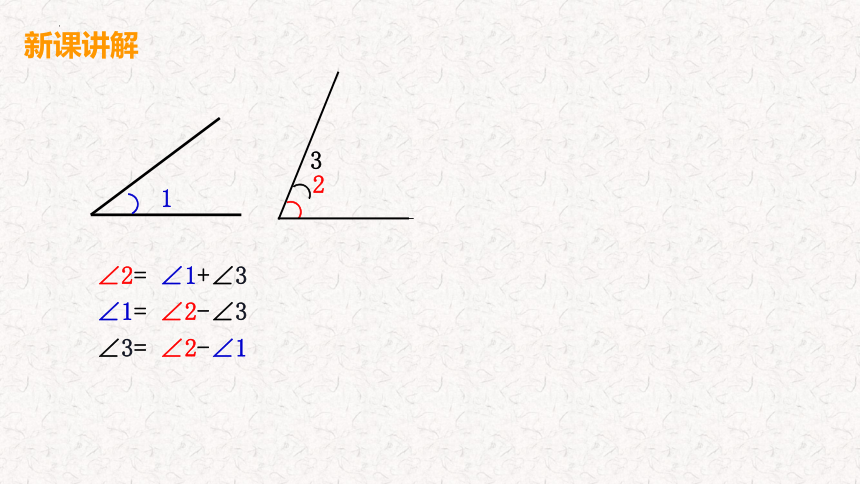
文档简介
(共20张PPT)
第四章 基本平面图形
第4节 角的比较
导入新课
讲授新课
课堂小结
随堂训练
学习目标
1.会比较角的大小,能估计一个角的大小.(重点)
2.会利用角的平分线的定义解决有关角的计算问题.(难点)
情境引入
选择从哪一面上山会感觉到舒缓呢?
成功永远属于肯攀高峰的人
!
情境引入
D
A
B
C
∠ABC>∠DCB
合作探究
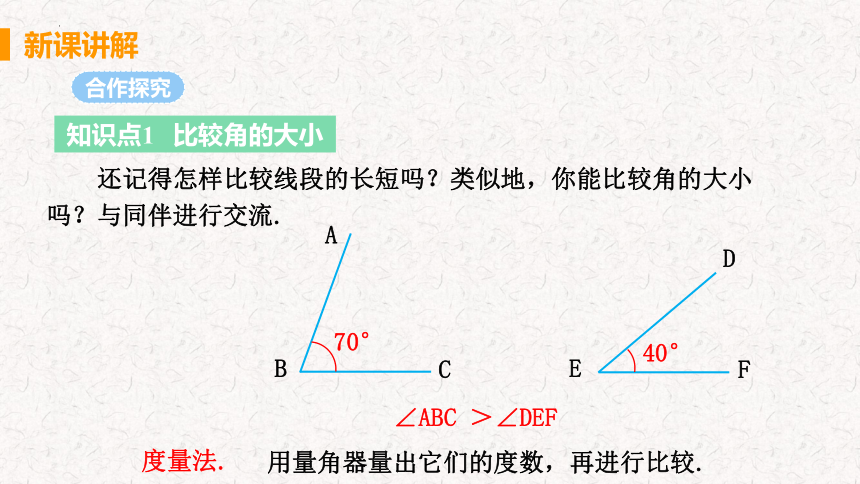
知识点1 比较角的大小
新课讲解
还记得怎样比较线段的长短吗?类似地,你能比较角的大小吗?与同伴进行交流.
度量法.
B
A
C
D
E
F
70°
40°
∠ABC >∠DEF
用量角器量出它们的度数,再进行比较.
新课讲解
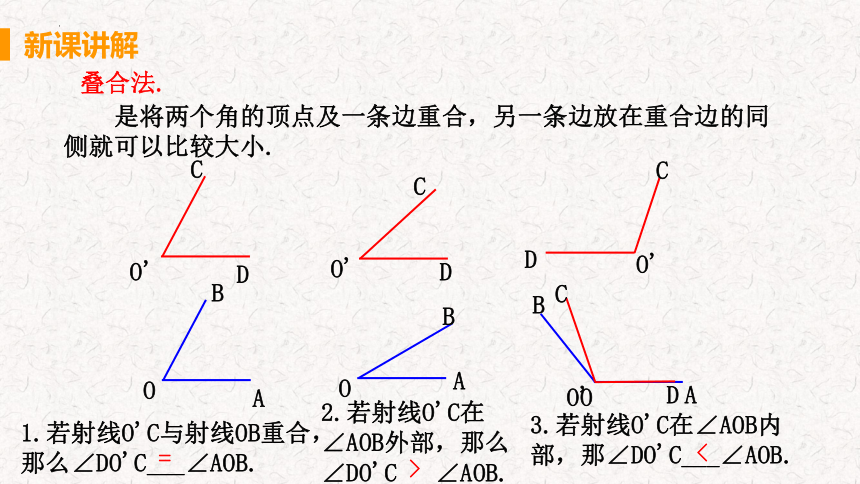
叠合法.
是将两个角的顶点及一条边重合,另一条边放在重合边的同侧就可以比较大小.
O
B
A
O'
C
D
O
B
A
O'
C
D
O
B
A
O'
C
D
1.若射线O'C与射线OB重合,那么∠DO'C___∠AOB.
2.若射线O'C在∠AOB外部,那么∠DO'C___∠AOB.
3.若射线O'C在∠AOB内部,那∠DO'C___∠AOB.
=
>
<
O'
C
D
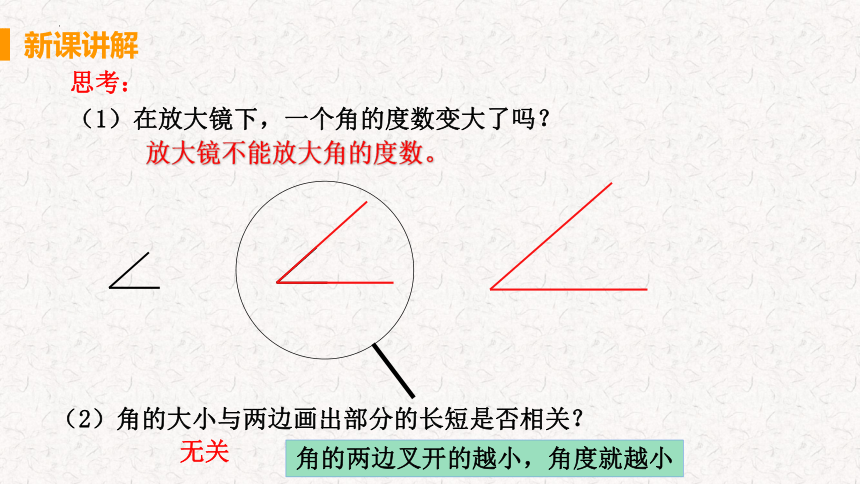
思考:
(1)在放大镜下,一个角的度数变大了吗?
放大镜不能放大角的度数。
新课讲解
(2)角的大小与两边画出部分的长短是否相关?
无关
角的两边叉开的越小,角度就越小
新课讲解
典例分析
例1.根据下图,回答下列问题:
(1)试比较∠AOB,∠AOD,∠AOE,∠AOC的大小,
并找出其中的锐角、直角、钝角、平角;
(2)试比较 ∠BOC 和 ∠DOE 的大小.
(3)小亮通过折叠的方法,使 OD 与 OC 重合,OE 落在 ∠BOC 的内部,所以∠BOC 大于 ∠DOE. 你能理解这种方法吗?
∠2= ∠1+∠3
∠1= ∠2-∠3
∠3= ∠2-∠1
⌒
2
⌒
1
3
⌒
新课讲解
解:(1)由图可知,∠AOB是平角,∠AOC是钝角,∠AOD是直角,∠AOE是锐角,
所以∠AOB>∠AOC>∠AOD>∠AOE.
(2)
新课讲解
典例分析
∠BOC>∠DOE
(3)折叠之后相当于把两个角的顶点及一边重合在一起,用第二种方法进行比较.
O
A
B
C
D
E
(4)请在图中画出小亮折叠的折痕 OF,∠DOF 与∠COF 有什么大小关系?
F
∠DOF = ∠COF
新课讲解
典例分析
新课讲解
做一做
思考:
当∠2= 2∠1时,∠1、∠3是什么关系?
⌒
2
⌒
⌒
3
1
O
A
C
B
从一个角的顶点出发的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.
角平分线的定义
新课讲解
符号语言
∵∠1=∠3 (或∠2= 2∠1,∠2= 2∠3)
∴射线OC是∠AOB平分线
∵射线OC平分∠AOB
∴∠1=∠3 (或∠2=2∠1,∠2=2∠3)
⌒
2
⌒
⌒
3
1
O
A
C
B
新课讲解
典例分析
例2.已知:∠AOB=76°,OC为∠AOB的角平分线,
那么∠AOC= ,∠AOC= ∠AOB,∠AOB= ∠COB
O
B
C
A
38°
2
新课讲解
例3.如图,已知点O为直线AB上一点,OM,ON分别是∠AOC,∠BOC的平分线,求∠MON的度数.
典例分析
新课讲解
解:因为点A,O,B在一条直线上,
所以∠AOB=180°.
因为∠AOC+∠BOC=∠AOB,
所以∠AOC+∠BOC=180°.
又因为OM,ON分别是∠AOC和∠BOC的平分线,
所以∠MOC= ∠AOC,∠CON= ∠BOC.
所以∠MOC+∠CON= (∠AOC+∠BOC)= ×180°=90°.
又因为∠MON=∠MOC+∠CON,
∴∠MON=90°.
当堂小练
1.如图,若∠AOC=∠BOD,那么∠AOD与∠BOC的关系是( )
A.∠AOD>∠BOC B.∠AOD<∠BOC
C.∠AOD=∠BOC D.无法确定
当堂小练
2.如图,∠AOB=50°,OC平分∠AOB,则∠AOC=________°.
当堂小练
3.如图,将长方形ABCD沿EF折叠,C点落在C′处,D点落在D′处.若∠EFC=119°,则∠BFC′为( )
A.58° B.45° C.60° D.42°
课堂小结
1.角的大小比较方法:度量法,叠合法
2.角度的换算
3.角平分线
4.方向角
第四章 基本平面图形
第4节 角的比较
导入新课
讲授新课
课堂小结
随堂训练
学习目标
1.会比较角的大小,能估计一个角的大小.(重点)
2.会利用角的平分线的定义解决有关角的计算问题.(难点)
情境引入
选择从哪一面上山会感觉到舒缓呢?
成功永远属于肯攀高峰的人
!
情境引入
D
A
B
C
∠ABC>∠DCB
合作探究
知识点1 比较角的大小
新课讲解
还记得怎样比较线段的长短吗?类似地,你能比较角的大小吗?与同伴进行交流.
度量法.
B
A
C
D
E
F
70°
40°
∠ABC >∠DEF
用量角器量出它们的度数,再进行比较.
新课讲解
叠合法.
是将两个角的顶点及一条边重合,另一条边放在重合边的同侧就可以比较大小.
O
B
A
O'
C
D
O
B
A
O'
C
D
O
B
A
O'
C
D
1.若射线O'C与射线OB重合,那么∠DO'C___∠AOB.
2.若射线O'C在∠AOB外部,那么∠DO'C___∠AOB.
3.若射线O'C在∠AOB内部,那∠DO'C___∠AOB.
=
>
<
O'
C
D
思考:
(1)在放大镜下,一个角的度数变大了吗?
放大镜不能放大角的度数。
新课讲解
(2)角的大小与两边画出部分的长短是否相关?
无关
角的两边叉开的越小,角度就越小
新课讲解
典例分析
例1.根据下图,回答下列问题:
(1)试比较∠AOB,∠AOD,∠AOE,∠AOC的大小,
并找出其中的锐角、直角、钝角、平角;
(2)试比较 ∠BOC 和 ∠DOE 的大小.
(3)小亮通过折叠的方法,使 OD 与 OC 重合,OE 落在 ∠BOC 的内部,所以∠BOC 大于 ∠DOE. 你能理解这种方法吗?
∠2= ∠1+∠3
∠1= ∠2-∠3
∠3= ∠2-∠1
⌒
2
⌒
1
3
⌒
新课讲解
解:(1)由图可知,∠AOB是平角,∠AOC是钝角,∠AOD是直角,∠AOE是锐角,
所以∠AOB>∠AOC>∠AOD>∠AOE.
(2)
新课讲解
典例分析
∠BOC>∠DOE
(3)折叠之后相当于把两个角的顶点及一边重合在一起,用第二种方法进行比较.
O
A
B
C
D
E
(4)请在图中画出小亮折叠的折痕 OF,∠DOF 与∠COF 有什么大小关系?
F
∠DOF = ∠COF
新课讲解
典例分析
新课讲解
做一做
思考:
当∠2= 2∠1时,∠1、∠3是什么关系?
⌒
2
⌒
⌒
3
1
O
A
C
B
从一个角的顶点出发的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.
角平分线的定义
新课讲解
符号语言
∵∠1=∠3 (或∠2= 2∠1,∠2= 2∠3)
∴射线OC是∠AOB平分线
∵射线OC平分∠AOB
∴∠1=∠3 (或∠2=2∠1,∠2=2∠3)
⌒
2
⌒
⌒
3
1
O
A
C
B
新课讲解
典例分析
例2.已知:∠AOB=76°,OC为∠AOB的角平分线,
那么∠AOC= ,∠AOC= ∠AOB,∠AOB= ∠COB
O
B
C
A
38°
2
新课讲解
例3.如图,已知点O为直线AB上一点,OM,ON分别是∠AOC,∠BOC的平分线,求∠MON的度数.
典例分析
新课讲解
解:因为点A,O,B在一条直线上,
所以∠AOB=180°.
因为∠AOC+∠BOC=∠AOB,
所以∠AOC+∠BOC=180°.
又因为OM,ON分别是∠AOC和∠BOC的平分线,
所以∠MOC= ∠AOC,∠CON= ∠BOC.
所以∠MOC+∠CON= (∠AOC+∠BOC)= ×180°=90°.
又因为∠MON=∠MOC+∠CON,
∴∠MON=90°.
当堂小练
1.如图,若∠AOC=∠BOD,那么∠AOD与∠BOC的关系是( )
A.∠AOD>∠BOC B.∠AOD<∠BOC
C.∠AOD=∠BOC D.无法确定
当堂小练
2.如图,∠AOB=50°,OC平分∠AOB,则∠AOC=________°.
当堂小练
3.如图,将长方形ABCD沿EF折叠,C点落在C′处,D点落在D′处.若∠EFC=119°,则∠BFC′为( )
A.58° B.45° C.60° D.42°
课堂小结
1.角的大小比较方法:度量法,叠合法
2.角度的换算
3.角平分线
4.方向角
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
