26.3 二次函数y=ax2+bx+c的图象(第3课时) 课件(共38张PPT)-2023-2024学年九年级数学上册同步精品课堂(沪教版)
文档属性
| 名称 | 26.3 二次函数y=ax2+bx+c的图象(第3课时) 课件(共38张PPT)-2023-2024学年九年级数学上册同步精品课堂(沪教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 19.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-11 00:00:00 | ||
图片预览










文档简介
(共38张PPT)
26.3二次函数y=ax +bx+c的图象(第3课时)
第26章 二次函数
教师
xxx
沪教版 九年级第一学期
代数问题
几何图形面积的最大值问题
01
02
CONTANTS
目 录
代数问题
01
在日常生活中存在着许许多多的与数学知识有关的实际问题.商品买卖过程中,作为商家追求利润最大化是永恒的追求.
如果你是商场经理,如何定价才能使商场获得最大利润呢?
情景引入
同学们在路边、闹市区经常会看到很多的大型广告牌,大家平常见到的广告牌一般什么形状的比较多
思考:现在一个广告公司接到了一笔业务,需要设计一块周长为12 m的矩形广告牌,由于公司一般根据广告牌面积的大小收取制作设计费,如果你是该公司的设计员,你能否设计出令广告公司老总满意的广告牌
情景引入
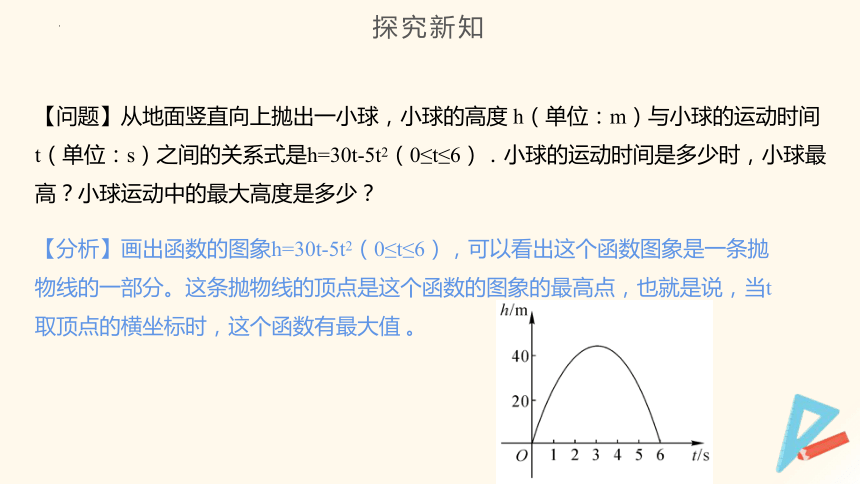
【问题】从地面竖直向上抛出一小球,小球的高度 h(单位:m)与小球的运动时间 t(单位:s)之间的关系式是h=30t-5t2(0≤t≤6).小球的运动时间是多少时,小球最高?小球运动中的最大高度是多少?
【分析】画出函数的图象h=30t-5t2(0≤t≤6),可以看出这个函数图象是一条抛物线的一部分。这条抛物线的顶点是这个函数的图象的最高点,也就是说,当t取顶点的横坐标时,这个函数有最大值 。
探究新知
因此,当t=-=-=3时,
h有最大值。
也就是说,小球运动的时间是3s时,小球最高,小球运动中的最大高度是45m。
探究新知
一般地,当a>0(a<0)时,抛物线y=ax2+bx+c的顶点是最低(高)点,也就是说,当x=-时,二次函数y=ax2+bx+c有最小(大)值。
探究新知
用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长l 的变化而变化。当l 是多少米时,场地的面积S最大?
矩形场地的周长是60m,一边长为l m,所以另一边长为(-l )m。场地的面积S=l (30-l ),
即S=-l 2+30l(0<l <30)。
因此,当l =-=-=15时,S有最大值==225,也就是说,当l是15m时,场地的面积S最大。
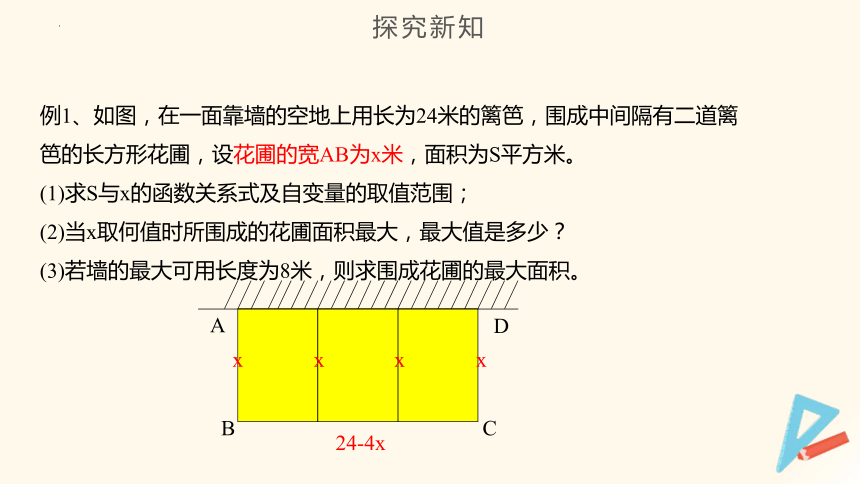
例1、如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米。
(1)求S与x的函数关系式及自变量的取值范围;
(2)当x取何值时所围成的花圃面积最大,最大值是多少?
(3)若墙的最大可用长度为8米,则求围成花圃的最大面积。
A
B
C
D
x
x
x
x
24-4x
探究新知
解:1)S=x(24-4x)=-4x2+24x(02)当x=-=3时,= = 36 ㎡
3) ∵墙的可用长度为8米
∴ 0<24-4x ≤8
∴ 4≤x<6
∴当x=4cm时,S最大值=32 平方米
探究新知
归纳总结
面积最值问题:
①找好自变量;
②利用相关的图象面积公式,列出函数关系式;
③利用函数的最值解决面积最值问题。注意:自变量的取决范围。
探究新知
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映;如调整价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出20件。已知商品的进价为每件40元,如果定价才能使利润最大?
【销售最大利润问题关键】
通过售价与利润关系得到二次函数的关系式,根据二次函数最值解决利润最值问题。
探究新知
1)设每件涨价x元,则此时每星期少卖______件,实际卖出________________件,此时每件产品的销售价为__________元,每周产品的销售额___________________元,此时每周产品的成本____________________元,因此周利润合计为:
y=(60+x)(300-10x)-40×(300-10x)
=-10x2+100x+6000
=+6250 (0≤x≤30)
当产品单价涨价5元,即售价65元,最大利润为6250元。
10x
300-10x
60+x
(60+x)(300-10x)
40×(300-10x)
探究新知
2)设每件降价a元,则此时每星期多卖______件,实际卖出________________件,此时每件产品的销售价为__________元,每周产品的销售额___________________元,此时每周产品的成本______________ 元,因此周利润合计为:
20a
300+20a
60-a
(60-a)(300+20a)
40×(300+20a)
y=(60-a)(300+20a)-40×(300+20a)
=-20a2+100a+6000
=+6125 (0≤a≤20)
当产品单价降价2.5元,即售价57.5元,最大利润为6125元。
探究新知
当产品单价降价2.5元,即售价57.5元,最大利润为6125元。
当产品单价涨价5元,即售价65元,最大利润为6250元。
当产品售价60元,利润为6000元。
综上所述,当涨价5元时利润最大,最大利润6250元。
探究新知
归纳总结
注意:
1. 用二次函数解实际问题时,审题是关键,检验容易被忽略,求得的结果除了要满足题中的数量关系,还要符合实际问题的意义.
2. 在实际问题中求最值时,解题思路是:列二次函数解析式,
①用配方法把函数解析式化为y=a(x-h)2+k的形式求函数的最值;
②针对函数解析式用顶点坐标公式求函数的最值.
探究新知
图示是抛物线形拱桥,当拱桥顶离水面2m时,水面宽4m。若水面下降1m,水面宽度增加多少?
探究新知
2m
4m
x
y
建立如图所示的直角坐标系,
设这条抛物线表示的二次函数为y=a
由抛物线过点(2,-2)得-2=a×4,a=-
所以这条抛物线表示的二次函数为
将y=-3带入二次函数得,
∴水面的宽度增加了(-4)m
新建坐标轴位置不同,所列方程不同
探究新知
2m
4m
x
0
y
建立如图所示直角坐标系,
设这条抛物线表示的二次函数为y=a+b
由抛物线过点(2,0)、(0,2)
所以这条抛物线表示的二次函数为+2
将y=-1带入二次函数得,
∴水面的宽度增加了(-4)m
探究新知
归纳总结
有关抛物线形的实际问题的一般解题思路。
(1)建立适当的平面直角坐标系。
(2)根据题意找出已知点的坐标。
(3)求出抛物线解析式。
(4)直接利用图象解决实际问题。
探究新知
几何图形面积的最大值问题
02
几何图形面积的最大值问题
例2:如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和CD分别在两直角边上.
(1)如果设矩形的一边AB=xm,那么AD边的长度如何表示?
F
E
A
C
D
40m
30m
B
思考:△CBF与△EAF有什么关系?有何启发?
探究新知
解: (1)∵AB=x,则BF=40-x.
∵BC∥AD,
∴△BCF∽△AEF.
即
F
E
A
C
D
40m
30m
B
x
40-x
探究新知
(2)设矩形的面积为ym ,当x取何值时,y的值最大?最大值是多少?
F
E
A
C
D
40m
30m
B
x
40-x
解: (2)由面积公式易得:
即
所以,当x=20时,y的值最大,最大为300.
即当AB=20cm时,矩形最大为300cm .
探究新知
变式:在上面的问题中,把矩形改为如图所示的位置,其他条件不变,那么矩形的最大面积是多少?
思考:类比原题的方法,能否利用相似表示AD?
A
C
D
40m
30m
B
O
E
F
探究新知
A
C
D
40m
30m
B
∟
∟
M
N
O
E
F
解:过点O作OM⊥EF交于AD与点N,由勾股定理易得EF=50cm,由等积法可得OM=24,
设AB=x,则MN=AB=x,易得ON=24-x,
由△AOD∽△FOE,得
即 ,
易得
所以当AB=12cm时,矩形最大为300cm .
探究新知
1.(2019山西中考)北中环桥是省城太原的一座跨汾河大桥(如图1),它由五个高度不同,跨径也不同的抛物线型钢拱通过吊桥,拉锁与主梁相连,最高的钢拱如图2所示,此钢拱(近似看成二次函数的图象-抛物线)在同一竖直平面内,与拱脚所在的水平面相交于A,B两点,拱高为78米(即最高点O到AB的距离为78米),跨径为90米(即AB=90米),以最高点O为坐标原点,以平行于AB的直线为轴建立平面直角坐标系,则此抛物线钢拱的函数表达式为( )
A. B. C. D.
B
探究新知
2.(2019合肥市中考)如图,隧道的截面由抛物线和长方形OABC构成,长方形的长OA是12m,宽OC是4m.按照图中所示的平面直角坐标系,抛物线可以用y=﹣x2+bx+c表示.在抛物线型拱璧上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m.那么两排灯的水平距离最小是( )
A.2m B.4m C.m D.m
D
探究新知
3. 足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线. 不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表: 下列结论:
①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t=4.5 ;
③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
B
探究新知
4.(2020贺州市中考)某学生在一平地上推铅球,铅球出手时离地面的高度为 米,出手后铅球在空中运动的高度y(米)与水平距离x(米)之间的函数关系式为,当铅球运行至与出手高度相等时,与出手点水平距离为8米,则该学生推铅球的成绩为________米.
10
探究新知
5.如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣k)2+h.已知球与D点的水平距离为6m时,达到最高2.6m,球网与D点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )
A.球不会过网 B.球会过球网但不会出界
C.球会过球网并会出界 D.无法确定
C
探究新知
6.如图,一座抛物线型拱桥,桥下水面宽度是4m时,拱高为2m,一艘木船宽2m.要能顺利从桥下通过,船顶点与桥拱之间的间隔应不少于0.3m,那么木船的高不得超______m.
x
y
O
1.2
探究新知
7.每年六、七月份某市荔枝大量上市,今年某水果商以5元/kg的价格购进一批荔枝进行销售,运输过程中质量损耗5%,运输费用是0.7元/kg,假设不计其他费用.(1)水果商要把荔枝售价至少定为 才不会亏本;
(2)在销售过程中,水果商发现每天荔枝的销售量m(kg)与销售单价x(元/kg)之间满足关系:m=-10x+120,那么当销售单价定为 时,每天获得的利润w最大.
6元
9元
探究新知
8.某商店试销一种新商品,新商品的进价为30元/件,经过一段时间的试销发现,每月的销售量会因售价的调整而不同.令每月销售量为y件,售价为x元/件,每月的总利润为Q元.
(1)当售价在40~50元时,每月销售量都为60件,则此时每月的总利润最多是多少元?
解:由题意得:当40≤x≤50时,
Q = 60(x-30)= 60x-1800
∵ y = 60 > 0,Q随x的增大而增大
∴当x最大= 50时,Q最大= 1200
答:此时每月的总利润最多是1200元.
探究新知
(2)当售价在50~70元时,每月销售量与售价的关系如图所示,则此时当该商品售价x是多少元时,该商店每月获利最大,最大利润是多少元?
解:当50≤x≤70时,
设y与x函数关系式为y=kx+b,
∵线段过(50,60)和(70,20).
50k+b=60
70k+b=20
∴
∴y =-2x +160(50≤x≤70)
解得:
k =-2
b = 160
探究新知
课堂小结
感谢观看
26.3二次函数y=ax +bx+c的图象(第3课时)
第26章 二次函数
教师
xxx
沪教版 九年级第一学期
代数问题
几何图形面积的最大值问题
01
02
CONTANTS
目 录
代数问题
01
在日常生活中存在着许许多多的与数学知识有关的实际问题.商品买卖过程中,作为商家追求利润最大化是永恒的追求.
如果你是商场经理,如何定价才能使商场获得最大利润呢?
情景引入
同学们在路边、闹市区经常会看到很多的大型广告牌,大家平常见到的广告牌一般什么形状的比较多
思考:现在一个广告公司接到了一笔业务,需要设计一块周长为12 m的矩形广告牌,由于公司一般根据广告牌面积的大小收取制作设计费,如果你是该公司的设计员,你能否设计出令广告公司老总满意的广告牌
情景引入
【问题】从地面竖直向上抛出一小球,小球的高度 h(单位:m)与小球的运动时间 t(单位:s)之间的关系式是h=30t-5t2(0≤t≤6).小球的运动时间是多少时,小球最高?小球运动中的最大高度是多少?
【分析】画出函数的图象h=30t-5t2(0≤t≤6),可以看出这个函数图象是一条抛物线的一部分。这条抛物线的顶点是这个函数的图象的最高点,也就是说,当t取顶点的横坐标时,这个函数有最大值 。
探究新知
因此,当t=-=-=3时,
h有最大值。
也就是说,小球运动的时间是3s时,小球最高,小球运动中的最大高度是45m。
探究新知
一般地,当a>0(a<0)时,抛物线y=ax2+bx+c的顶点是最低(高)点,也就是说,当x=-时,二次函数y=ax2+bx+c有最小(大)值。
探究新知
用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长l 的变化而变化。当l 是多少米时,场地的面积S最大?
矩形场地的周长是60m,一边长为l m,所以另一边长为(-l )m。场地的面积S=l (30-l ),
即S=-l 2+30l(0<l <30)。
因此,当l =-=-=15时,S有最大值==225,也就是说,当l是15m时,场地的面积S最大。
例1、如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米。
(1)求S与x的函数关系式及自变量的取值范围;
(2)当x取何值时所围成的花圃面积最大,最大值是多少?
(3)若墙的最大可用长度为8米,则求围成花圃的最大面积。
A
B
C
D
x
x
x
x
24-4x
探究新知
解:1)S=x(24-4x)=-4x2+24x(0
3) ∵墙的可用长度为8米
∴ 0<24-4x ≤8
∴ 4≤x<6
∴当x=4cm时,S最大值=32 平方米
探究新知
归纳总结
面积最值问题:
①找好自变量;
②利用相关的图象面积公式,列出函数关系式;
③利用函数的最值解决面积最值问题。注意:自变量的取决范围。
探究新知
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映;如调整价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出20件。已知商品的进价为每件40元,如果定价才能使利润最大?
【销售最大利润问题关键】
通过售价与利润关系得到二次函数的关系式,根据二次函数最值解决利润最值问题。
探究新知
1)设每件涨价x元,则此时每星期少卖______件,实际卖出________________件,此时每件产品的销售价为__________元,每周产品的销售额___________________元,此时每周产品的成本____________________元,因此周利润合计为:
y=(60+x)(300-10x)-40×(300-10x)
=-10x2+100x+6000
=+6250 (0≤x≤30)
当产品单价涨价5元,即售价65元,最大利润为6250元。
10x
300-10x
60+x
(60+x)(300-10x)
40×(300-10x)
探究新知
2)设每件降价a元,则此时每星期多卖______件,实际卖出________________件,此时每件产品的销售价为__________元,每周产品的销售额___________________元,此时每周产品的成本______________ 元,因此周利润合计为:
20a
300+20a
60-a
(60-a)(300+20a)
40×(300+20a)
y=(60-a)(300+20a)-40×(300+20a)
=-20a2+100a+6000
=+6125 (0≤a≤20)
当产品单价降价2.5元,即售价57.5元,最大利润为6125元。
探究新知
当产品单价降价2.5元,即售价57.5元,最大利润为6125元。
当产品单价涨价5元,即售价65元,最大利润为6250元。
当产品售价60元,利润为6000元。
综上所述,当涨价5元时利润最大,最大利润6250元。
探究新知
归纳总结
注意:
1. 用二次函数解实际问题时,审题是关键,检验容易被忽略,求得的结果除了要满足题中的数量关系,还要符合实际问题的意义.
2. 在实际问题中求最值时,解题思路是:列二次函数解析式,
①用配方法把函数解析式化为y=a(x-h)2+k的形式求函数的最值;
②针对函数解析式用顶点坐标公式求函数的最值.
探究新知
图示是抛物线形拱桥,当拱桥顶离水面2m时,水面宽4m。若水面下降1m,水面宽度增加多少?
探究新知
2m
4m
x
y
建立如图所示的直角坐标系,
设这条抛物线表示的二次函数为y=a
由抛物线过点(2,-2)得-2=a×4,a=-
所以这条抛物线表示的二次函数为
将y=-3带入二次函数得,
∴水面的宽度增加了(-4)m
新建坐标轴位置不同,所列方程不同
探究新知
2m
4m
x
0
y
建立如图所示直角坐标系,
设这条抛物线表示的二次函数为y=a+b
由抛物线过点(2,0)、(0,2)
所以这条抛物线表示的二次函数为+2
将y=-1带入二次函数得,
∴水面的宽度增加了(-4)m
探究新知
归纳总结
有关抛物线形的实际问题的一般解题思路。
(1)建立适当的平面直角坐标系。
(2)根据题意找出已知点的坐标。
(3)求出抛物线解析式。
(4)直接利用图象解决实际问题。
探究新知
几何图形面积的最大值问题
02
几何图形面积的最大值问题
例2:如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和CD分别在两直角边上.
(1)如果设矩形的一边AB=xm,那么AD边的长度如何表示?
F
E
A
C
D
40m
30m
B
思考:△CBF与△EAF有什么关系?有何启发?
探究新知
解: (1)∵AB=x,则BF=40-x.
∵BC∥AD,
∴△BCF∽△AEF.
即
F
E
A
C
D
40m
30m
B
x
40-x
探究新知
(2)设矩形的面积为ym ,当x取何值时,y的值最大?最大值是多少?
F
E
A
C
D
40m
30m
B
x
40-x
解: (2)由面积公式易得:
即
所以,当x=20时,y的值最大,最大为300.
即当AB=20cm时,矩形最大为300cm .
探究新知
变式:在上面的问题中,把矩形改为如图所示的位置,其他条件不变,那么矩形的最大面积是多少?
思考:类比原题的方法,能否利用相似表示AD?
A
C
D
40m
30m
B
O
E
F
探究新知
A
C
D
40m
30m
B
∟
∟
M
N
O
E
F
解:过点O作OM⊥EF交于AD与点N,由勾股定理易得EF=50cm,由等积法可得OM=24,
设AB=x,则MN=AB=x,易得ON=24-x,
由△AOD∽△FOE,得
即 ,
易得
所以当AB=12cm时,矩形最大为300cm .
探究新知
1.(2019山西中考)北中环桥是省城太原的一座跨汾河大桥(如图1),它由五个高度不同,跨径也不同的抛物线型钢拱通过吊桥,拉锁与主梁相连,最高的钢拱如图2所示,此钢拱(近似看成二次函数的图象-抛物线)在同一竖直平面内,与拱脚所在的水平面相交于A,B两点,拱高为78米(即最高点O到AB的距离为78米),跨径为90米(即AB=90米),以最高点O为坐标原点,以平行于AB的直线为轴建立平面直角坐标系,则此抛物线钢拱的函数表达式为( )
A. B. C. D.
B
探究新知
2.(2019合肥市中考)如图,隧道的截面由抛物线和长方形OABC构成,长方形的长OA是12m,宽OC是4m.按照图中所示的平面直角坐标系,抛物线可以用y=﹣x2+bx+c表示.在抛物线型拱璧上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m.那么两排灯的水平距离最小是( )
A.2m B.4m C.m D.m
D
探究新知
3. 足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线. 不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表: 下列结论:
①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t=4.5 ;
③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
B
探究新知
4.(2020贺州市中考)某学生在一平地上推铅球,铅球出手时离地面的高度为 米,出手后铅球在空中运动的高度y(米)与水平距离x(米)之间的函数关系式为,当铅球运行至与出手高度相等时,与出手点水平距离为8米,则该学生推铅球的成绩为________米.
10
探究新知
5.如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣k)2+h.已知球与D点的水平距离为6m时,达到最高2.6m,球网与D点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )
A.球不会过网 B.球会过球网但不会出界
C.球会过球网并会出界 D.无法确定
C
探究新知
6.如图,一座抛物线型拱桥,桥下水面宽度是4m时,拱高为2m,一艘木船宽2m.要能顺利从桥下通过,船顶点与桥拱之间的间隔应不少于0.3m,那么木船的高不得超______m.
x
y
O
1.2
探究新知
7.每年六、七月份某市荔枝大量上市,今年某水果商以5元/kg的价格购进一批荔枝进行销售,运输过程中质量损耗5%,运输费用是0.7元/kg,假设不计其他费用.(1)水果商要把荔枝售价至少定为 才不会亏本;
(2)在销售过程中,水果商发现每天荔枝的销售量m(kg)与销售单价x(元/kg)之间满足关系:m=-10x+120,那么当销售单价定为 时,每天获得的利润w最大.
6元
9元
探究新知
8.某商店试销一种新商品,新商品的进价为30元/件,经过一段时间的试销发现,每月的销售量会因售价的调整而不同.令每月销售量为y件,售价为x元/件,每月的总利润为Q元.
(1)当售价在40~50元时,每月销售量都为60件,则此时每月的总利润最多是多少元?
解:由题意得:当40≤x≤50时,
Q = 60(x-30)= 60x-1800
∵ y = 60 > 0,Q随x的增大而增大
∴当x最大= 50时,Q最大= 1200
答:此时每月的总利润最多是1200元.
探究新知
(2)当售价在50~70元时,每月销售量与售价的关系如图所示,则此时当该商品售价x是多少元时,该商店每月获利最大,最大利润是多少元?
解:当50≤x≤70时,
设y与x函数关系式为y=kx+b,
∵线段过(50,60)和(70,20).
50k+b=60
70k+b=20
∴
∴y =-2x +160(50≤x≤70)
解得:
k =-2
b = 160
探究新知
课堂小结
感谢观看
