山东省泰安市东平县沙河站镇中学数学(青岛版)八年级下册:10.5一次函数与一元一次不等式
文档属性
| 名称 | 山东省泰安市东平县沙河站镇中学数学(青岛版)八年级下册:10.5一次函数与一元一次不等式 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-24 07:56:17 | ||
图片预览





文档简介
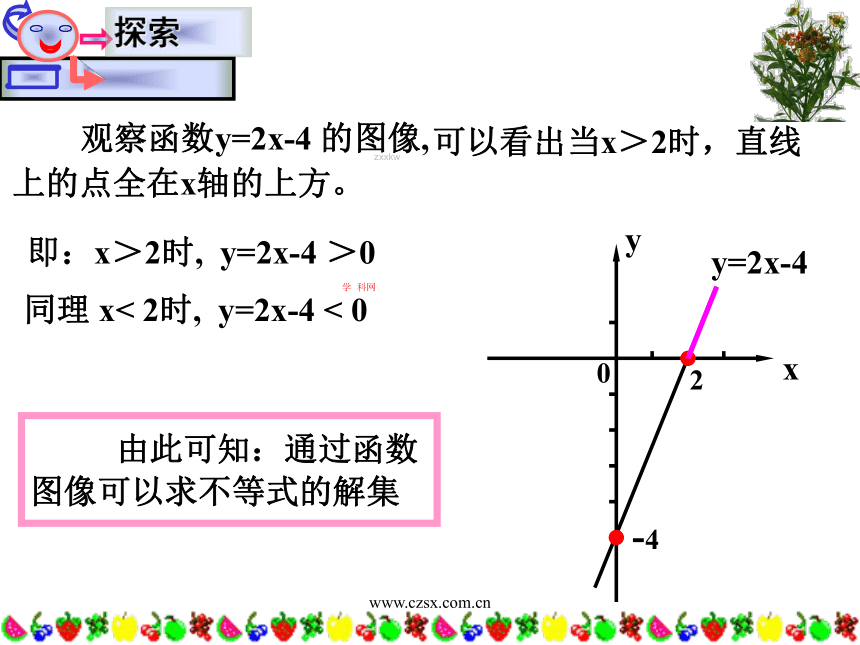
课件23张PPT。www.czsx.com.cn八年级《数学》下册 10.5 一次函数与一元一次不等式沙河站中学 王承梅zxxkwwww.czsx.com.cn思考: (1)以下两个问题是不是同一个问题?
①解不等式:2x-4>0
②当x为何值时,函数y=2x -4的值大于0?
(2)你如何利用图象来说明②?
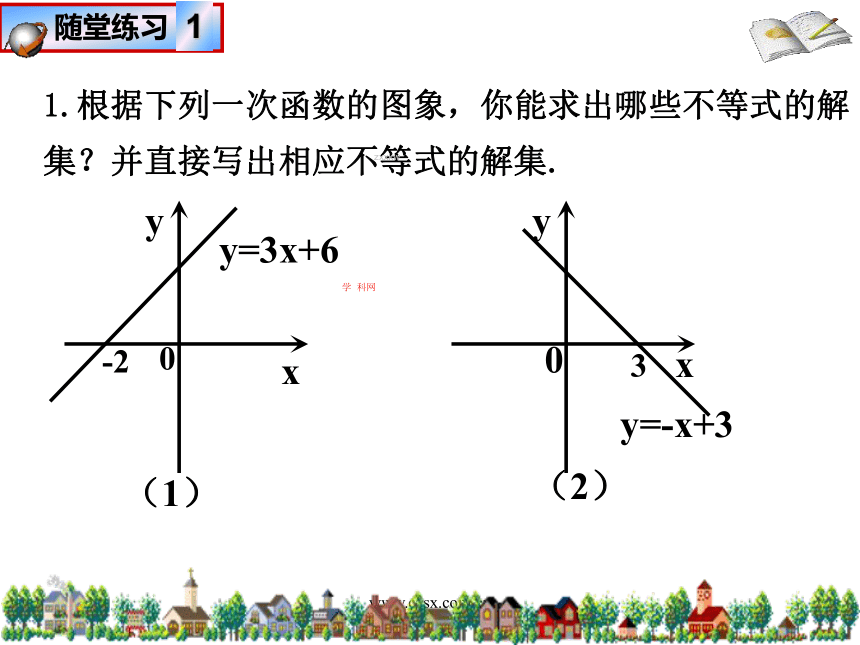
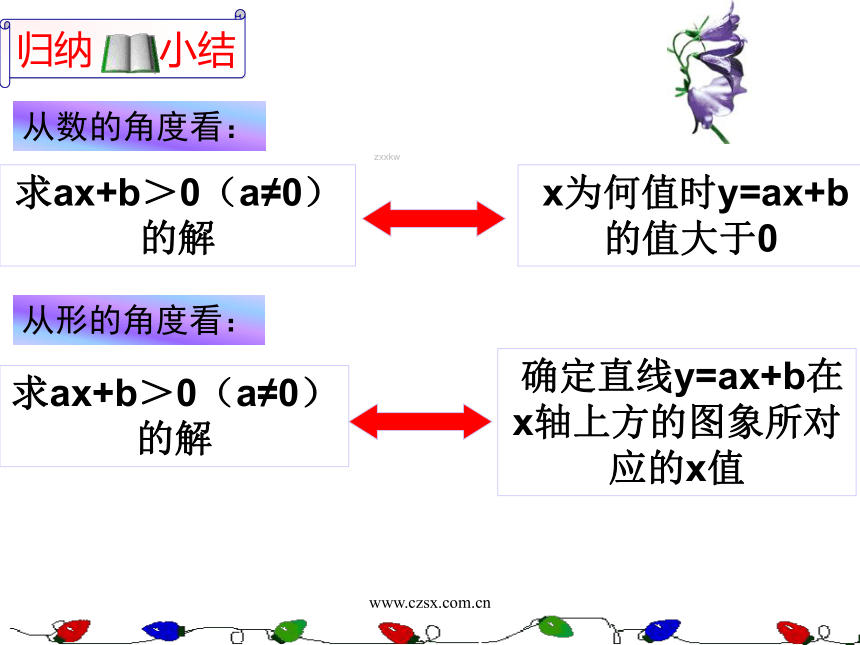
(3)“解不等式2x-4<0”可以与怎样的一次函数问题是同一的?怎样在图象上加以说明?zxxkw学 科网www.czsx.com.cny=2x-4即:x>2时, y=2x-4 >0 由此可知:通过函数图像可以求不等式的解集同理 x< 2时, y=2x-4 < 0zxxkw学 科网www.czsx.com.cn“解不等式ax+b>0(a,b为常数,a≠0)”与“求自变量x为什么范围内,一次函数y=ax+b的值大于0”有什么关系?(同一个问题) 由于任何一元一次不等式都可以转化为ax+b>0或ax +b <0(a,b为常数,a≠0)的形式, 所以解一元一次不等式可以看作:当一次函数值大于(或小于)于0时,求自变量相应的取值范围.zxxkw学 科网www.czsx.com.cn1.根据下列一次函数的图象,你能求出哪些不等式的解集?并直接写出相应不等式的解集.zxxkw学 科网www.czsx.com.cnx=2x<2x≥2X>2zxxkw学 科网www.czsx.com.cn从数的角度看:求ax+b>0(a≠0)的解 x为何值时y=ax+b的值大于0求ax+b>0(a≠0)的解 确定直线y=ax+b在x轴上方的图象所对应的x值从形的角度看:zxxkwwww.czsx.com.cn解(1)移项得:5x - 3x > 10 - 6合并,得 2x > 4∴原不等式的解是: x>2化系数为1,得x >2(2)作出函数 y = 2x -4 的图象(如图)从图知观察知,当x>2时 y 的值在x轴上方,即 y > 0因此当 x > 2 时函数的值大于0。zxxkw学 科网www.czsx.com.cnzxxkw学 科网学 科网www.czsx.com.cn例题:用画函数图象的方法解不等式5x+4<2x+10解法1:原不等式化为3x -6<0,画出直线y = 3x -6(如图) 可以看出,当x<2 时这条直线上
的点在x轴的下方,即这时y = 3x -6 <0
所以不等式的解集为x<2zxxkw学 科网www.czsx.com.cn解法二:画出函数 y = 2x+10 y = 5x+4图象 从图中看出:当x <2时直线 y = 5x +4 在 y = 2x +10的下方 即 5x+4 < 2x +10∴ 不等式 5x+4 < 2 x +10 的解集是x < 2学 科网www.czsx.com.cn已知一次函数 y = 2x+1,根据它的图象回答下列问题.
(1) x 取什么值时,函数值 y 为1?
(2) x 取什么值时,函数值 y 大于3?
(3) x 取什么值时,函数值 y 小于3?解:作出函数 y = 2x+1的图象及直线y = 3 (如图)y = 2x +1y= 3从图中可知:(1)当 x = 0.5时,函数值 y 为1。(2)当x > 1.5 时,函数值 y 大于3。(3)当x <1 .5时,函数值 y 小于3。学 科网www.czsx.com.cn利用图象求不等式6x-3<x+2的解方法一:将方程变形为ax+b<0的形式5x-5<0转化为函数解析式画图象y=5x-5方法二:把不等式6x-3<x+2的两边看成是两个函数:即y1=6x-3,y2=x+2转化为两个函数画出两个函数图象找出交点(观察x在什么范围时图象 y1点在y2点的下方)0-1yx1所以不等式6x-3<x+2的解是x<1所以不等式6x-3<x+2的解是x<1(观察x在什么范围时图象上的点是x轴下方)学 科网www.czsx.com.cnwww.czsx.com.cn 1、某单位准备和一个体车主或一国营出租车公司中
的一家签订月租车合同,设汽车每月行驶x 千米,个体车
主收费y1元,国营出租车公司收费为y2元,观察下列图象
可知(如图1-5-2),当x________时,选用个体车较合算. 2、当自变量 x 的取值满足什么条件时,
函数 y = 3x+8 的值满足下列条件?
y = 0 (2) y = -7
(3) y >0 (4) y < 2
3、用图象法解方程
(1)5x -1 = 2x + 5www.czsx.com.cn1.范围为什么时,函数y=2x+6的值满足以下条件?
(1) y=0 (2) y>0
2.利用图像解不等式:5x-1 >2x+53、作出函数y=-2x-5的图象,观察图象回答下列问题:
① x取什么值时,-2x-5=0?
② x取什么值时,-2x-5>0?
③ x取什么值时,-2x-5≤0?
④ x取什么值时,-2x-5<0?x=-3x>-3x>2www.czsx.com.cn1.若y1=-x+3,y2=3x+4,当x取何值时,y1>y2?2.兄弟俩赛跑,哥哥先让弟弟跑9m,然后自己才开始跑.已知弟弟每秒跑3m,哥哥每秒跑4m.列出函数关系式,作出函数图象,观察图象回答下列问题:
(1)何时弟弟跑在哥哥前面?
(2)何时哥哥跑在弟弟前面?
(3)谁先跑过20m?谁先跑过100m?0至12秒12秒之后弟弟先跑过20m,哥哥先跑过100米www.czsx.com.cn通过这节课的学习,你有什么收获?用一次函数图象来解一元一次不等式一次函数、一元一次不等式之间的联系www.czsx.com.cn 由上面两个问题的关系,能进一步得到“解不等式ax+b >0或ax+b < 0(a,b为常数)”与“求自变量x为何值时,一次函数y = ax+b 的函数值大于0或一次函数y = ax+b 的函数值小于0”有什么关系?由于任何一元一次不等式都可以转化为ax+b>0或ax+b < 0(a,b为常数a≠0)的形式,所以解一元一次不等式可以转化为:当一次函数值大(小)于0时,求自变量相应的取值范围。www.czsx.com.cn 由于一次函数图象是一条直线,它与x轴相交,在x轴上方的图象对应的函数值y大于0,则图象对应的自变量x为相应的自变量取值范围;在x轴下方的图象对应的函数值y小于0,则图象对应的自变量x为相应的自变量取值范围。也是相应的不等式的解集。2、如图,直线L1, L2交于一点P,若y1 ≥y2 ,则( )
x ≥ 3
x ≤3
2 ≤ x ≤ 3
x ≤ 41、已知函数Y=3X+8,当X————————,函数
的值等于0。当X————————,函数的值大于0。当X———————— ,函数的值不大于2。= ≤- 2>B巩固练习www.czsx.com.cn3.已知函数 (1)当y>0时, x的取值范围是 . (2)当y<0.5 时, x的取值范围是 . (3)当-1≤y≤1时, x的取值范围是 .4、已知一次函数y=kx+b(k≠0)的图象与坐标轴的交点分别为(-1,0)和(0,-2),
则不等式kx+b<0的解集是( )
A、x>-2; B、x<-2
C、x>-1; D、x<-1.www.czsx.com.cn4、已知一次函数y=kx+b(k≠0)的图象与坐标轴的交点分别为(-1,0)和(0,-2),
则不等式kx+b<0的解集是( )
A、x>-2; B、x<-2
C、x>-1; D、x<-1.
①解不等式:2x-4>0
②当x为何值时,函数y=2x -4的值大于0?
(2)你如何利用图象来说明②?
(3)“解不等式2x-4<0”可以与怎样的一次函数问题是同一的?怎样在图象上加以说明?zxxkw学 科网www.czsx.com.cny=2x-4即:x>2时, y=2x-4 >0 由此可知:通过函数图像可以求不等式的解集同理 x< 2时, y=2x-4 < 0zxxkw学 科网www.czsx.com.cn“解不等式ax+b>0(a,b为常数,a≠0)”与“求自变量x为什么范围内,一次函数y=ax+b的值大于0”有什么关系?(同一个问题) 由于任何一元一次不等式都可以转化为ax+b>0或ax +b <0(a,b为常数,a≠0)的形式, 所以解一元一次不等式可以看作:当一次函数值大于(或小于)于0时,求自变量相应的取值范围.zxxkw学 科网www.czsx.com.cn1.根据下列一次函数的图象,你能求出哪些不等式的解集?并直接写出相应不等式的解集.zxxkw学 科网www.czsx.com.cnx=2x<2x≥2X>2zxxkw学 科网www.czsx.com.cn从数的角度看:求ax+b>0(a≠0)的解 x为何值时y=ax+b的值大于0求ax+b>0(a≠0)的解 确定直线y=ax+b在x轴上方的图象所对应的x值从形的角度看:zxxkwwww.czsx.com.cn解(1)移项得:5x - 3x > 10 - 6合并,得 2x > 4∴原不等式的解是: x>2化系数为1,得x >2(2)作出函数 y = 2x -4 的图象(如图)从图知观察知,当x>2时 y 的值在x轴上方,即 y > 0因此当 x > 2 时函数的值大于0。zxxkw学 科网www.czsx.com.cnzxxkw学 科网学 科网www.czsx.com.cn例题:用画函数图象的方法解不等式5x+4<2x+10解法1:原不等式化为3x -6<0,画出直线y = 3x -6(如图) 可以看出,当x<2 时这条直线上
的点在x轴的下方,即这时y = 3x -6 <0
所以不等式的解集为x<2zxxkw学 科网www.czsx.com.cn解法二:画出函数 y = 2x+10 y = 5x+4图象 从图中看出:当x <2时直线 y = 5x +4 在 y = 2x +10的下方 即 5x+4 < 2x +10∴ 不等式 5x+4 < 2 x +10 的解集是x < 2学 科网www.czsx.com.cn已知一次函数 y = 2x+1,根据它的图象回答下列问题.
(1) x 取什么值时,函数值 y 为1?
(2) x 取什么值时,函数值 y 大于3?
(3) x 取什么值时,函数值 y 小于3?解:作出函数 y = 2x+1的图象及直线y = 3 (如图)y = 2x +1y= 3从图中可知:(1)当 x = 0.5时,函数值 y 为1。(2)当x > 1.5 时,函数值 y 大于3。(3)当x <1 .5时,函数值 y 小于3。学 科网www.czsx.com.cn利用图象求不等式6x-3<x+2的解方法一:将方程变形为ax+b<0的形式5x-5<0转化为函数解析式画图象y=5x-5方法二:把不等式6x-3<x+2的两边看成是两个函数:即y1=6x-3,y2=x+2转化为两个函数画出两个函数图象找出交点(观察x在什么范围时图象 y1点在y2点的下方)0-1yx1所以不等式6x-3<x+2的解是x<1所以不等式6x-3<x+2的解是x<1(观察x在什么范围时图象上的点是x轴下方)学 科网www.czsx.com.cnwww.czsx.com.cn 1、某单位准备和一个体车主或一国营出租车公司中
的一家签订月租车合同,设汽车每月行驶x 千米,个体车
主收费y1元,国营出租车公司收费为y2元,观察下列图象
可知(如图1-5-2),当x________时,选用个体车较合算. 2、当自变量 x 的取值满足什么条件时,
函数 y = 3x+8 的值满足下列条件?
y = 0 (2) y = -7
(3) y >0 (4) y < 2
3、用图象法解方程
(1)5x -1 = 2x + 5www.czsx.com.cn1.范围为什么时,函数y=2x+6的值满足以下条件?
(1) y=0 (2) y>0
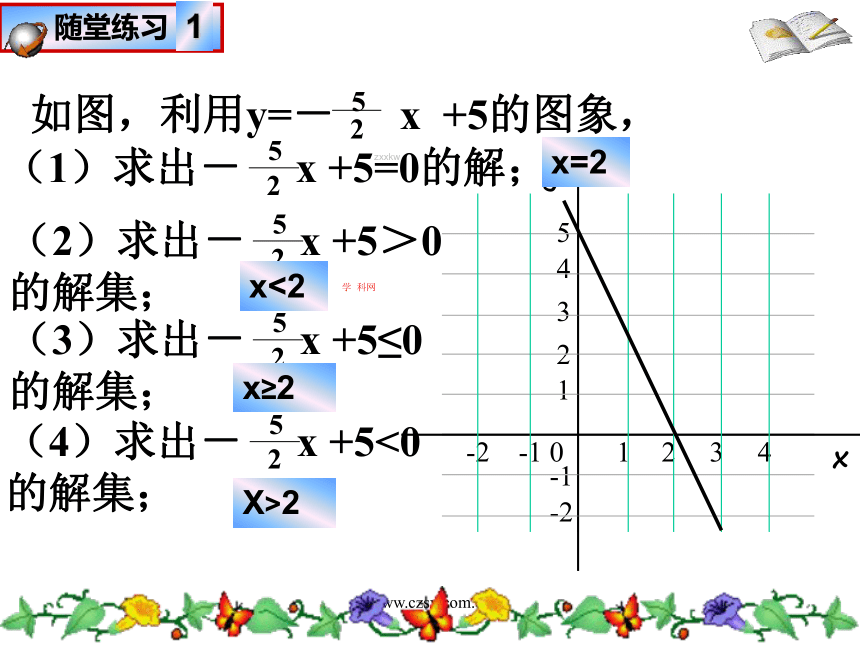
2.利用图像解不等式:5x-1 >2x+53、作出函数y=-2x-5的图象,观察图象回答下列问题:
① x取什么值时,-2x-5=0?
② x取什么值时,-2x-5>0?
③ x取什么值时,-2x-5≤0?
④ x取什么值时,-2x-5<0?x=-3x>-3x>2www.czsx.com.cn1.若y1=-x+3,y2=3x+4,当x取何值时,y1>y2?2.兄弟俩赛跑,哥哥先让弟弟跑9m,然后自己才开始跑.已知弟弟每秒跑3m,哥哥每秒跑4m.列出函数关系式,作出函数图象,观察图象回答下列问题:
(1)何时弟弟跑在哥哥前面?
(2)何时哥哥跑在弟弟前面?
(3)谁先跑过20m?谁先跑过100m?0至12秒12秒之后弟弟先跑过20m,哥哥先跑过100米www.czsx.com.cn通过这节课的学习,你有什么收获?用一次函数图象来解一元一次不等式一次函数、一元一次不等式之间的联系www.czsx.com.cn 由上面两个问题的关系,能进一步得到“解不等式ax+b >0或ax+b < 0(a,b为常数)”与“求自变量x为何值时,一次函数y = ax+b 的函数值大于0或一次函数y = ax+b 的函数值小于0”有什么关系?由于任何一元一次不等式都可以转化为ax+b>0或ax+b < 0(a,b为常数a≠0)的形式,所以解一元一次不等式可以转化为:当一次函数值大(小)于0时,求自变量相应的取值范围。www.czsx.com.cn 由于一次函数图象是一条直线,它与x轴相交,在x轴上方的图象对应的函数值y大于0,则图象对应的自变量x为相应的自变量取值范围;在x轴下方的图象对应的函数值y小于0,则图象对应的自变量x为相应的自变量取值范围。也是相应的不等式的解集。2、如图,直线L1, L2交于一点P,若y1 ≥y2 ,则( )
x ≥ 3
x ≤3
2 ≤ x ≤ 3
x ≤ 41、已知函数Y=3X+8,当X————————,函数
的值等于0。当X————————,函数的值大于0。当X———————— ,函数的值不大于2。= ≤- 2>B巩固练习www.czsx.com.cn3.已知函数 (1)当y>0时, x的取值范围是 . (2)当y<0.5 时, x的取值范围是 . (3)当-1≤y≤1时, x的取值范围是 .4、已知一次函数y=kx+b(k≠0)的图象与坐标轴的交点分别为(-1,0)和(0,-2),
则不等式kx+b<0的解集是( )
A、x>-2; B、x<-2
C、x>-1; D、x<-1.www.czsx.com.cn4、已知一次函数y=kx+b(k≠0)的图象与坐标轴的交点分别为(-1,0)和(0,-2),
则不等式kx+b<0的解集是( )
A、x>-2; B、x<-2
C、x>-1; D、x<-1.
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
