17.1勾股定理第2课时
文档属性
| 名称 | 17.1勾股定理第2课时 |  | |
| 格式 | zip | ||
| 文件大小 | 302.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-24 11:21:03 | ||
图片预览


文档简介
课件19张PPT。第十七章 勾股定理
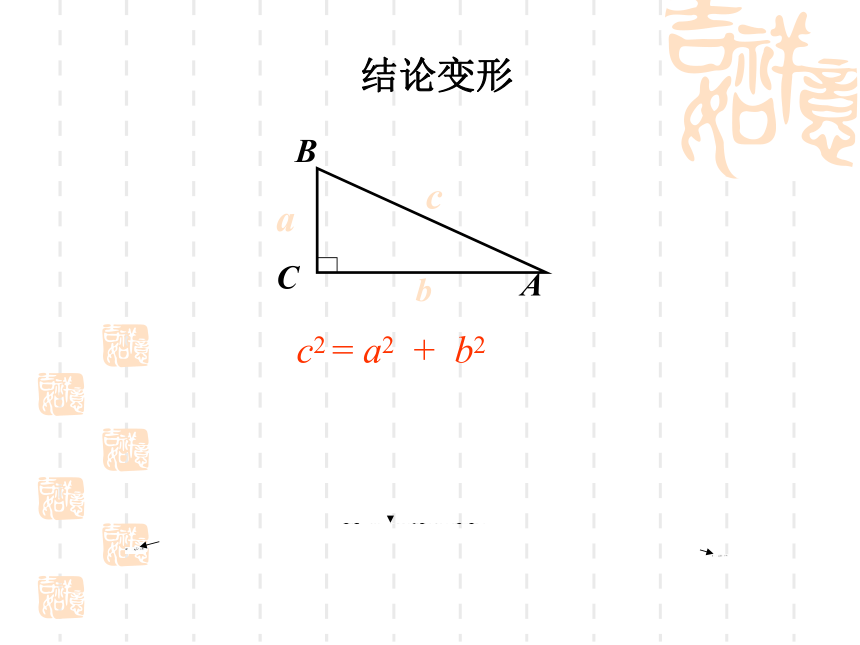
17.1 勾股定理(二)勾股定理:直角三角形两直角边的平方和等于斜边的平方.回 顾 活 动 1如果在Rt△ ABC中,∠C=90°,
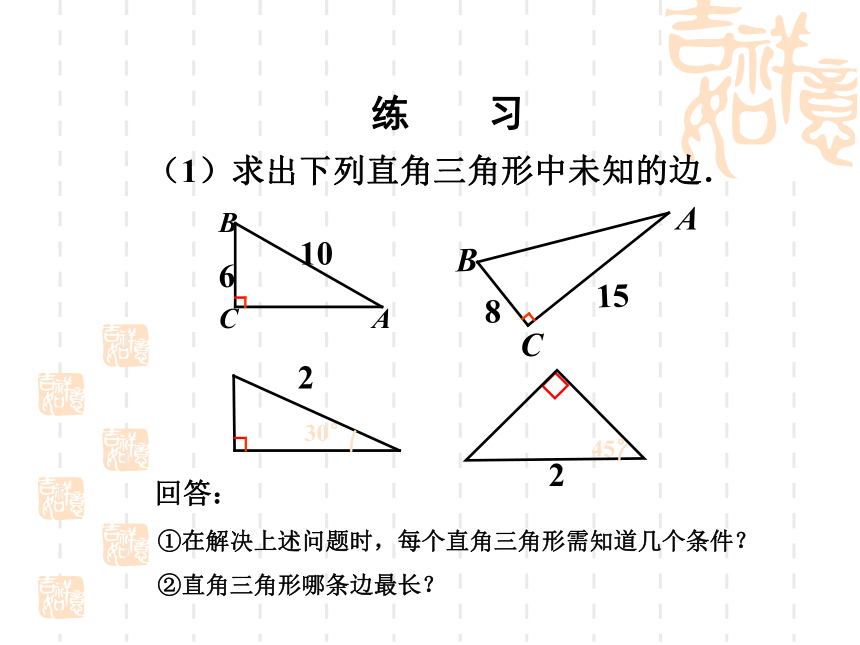
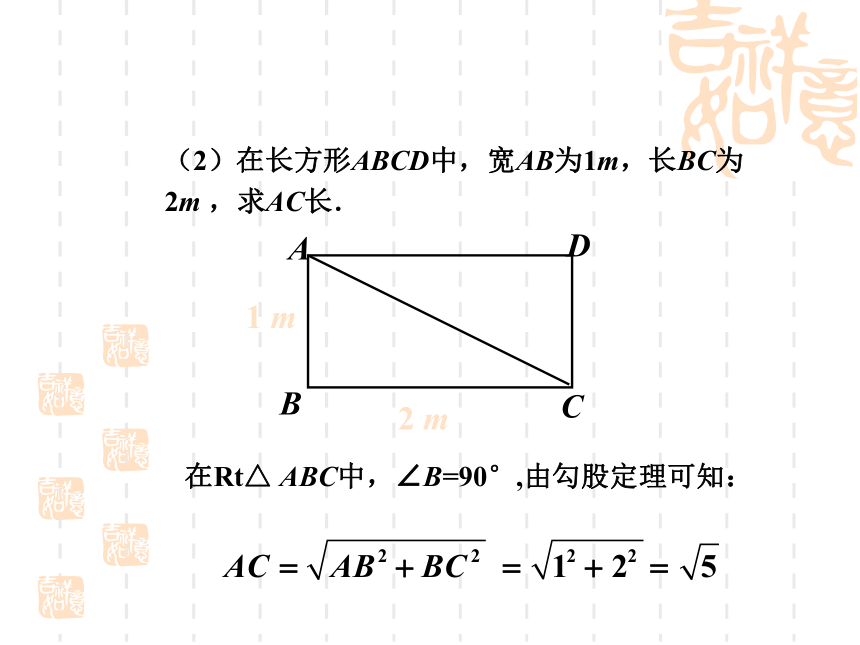
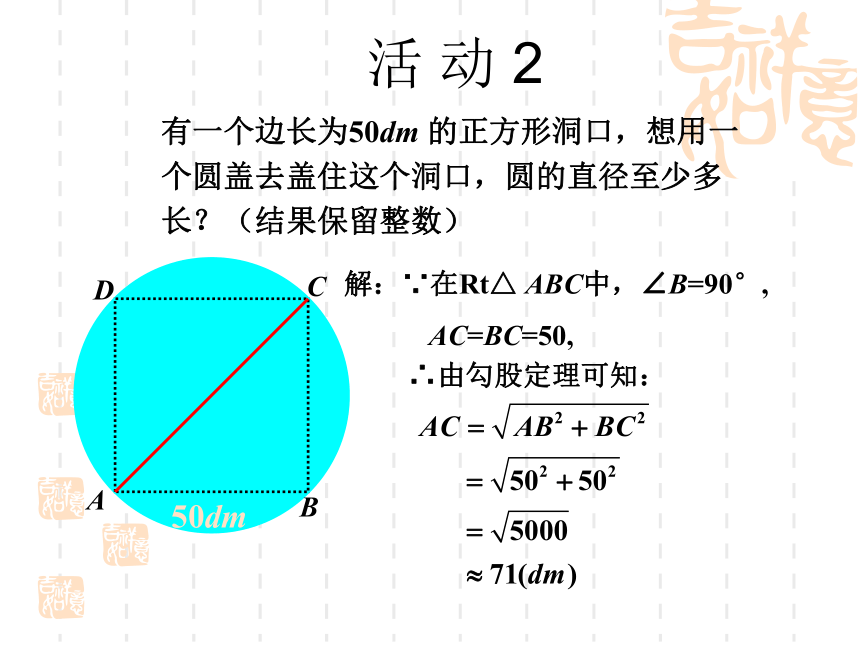
那么结论变形c2 = a2 + b2(1)求出下列直角三角形中未知的边.练 习回答:①在解决上述问题时,每个直角三角形需知道几个条件?②直角三角形哪条边最长?(2)在长方形ABCD中,宽AB为1m,长BC为2m ,求AC长.1 m2 m在Rt△ ABC中,∠B=90°,由勾股定理可知:有一个边长为50dm 的正方形洞口,想用一个圆盖去盖住这个洞口,圆的直径至少多长?(结果保留整数)50dmABCD解:∵在Rt△ ABC中,∠B=90°,
AC=BC=50,∴由勾股定理可知:活 动 2
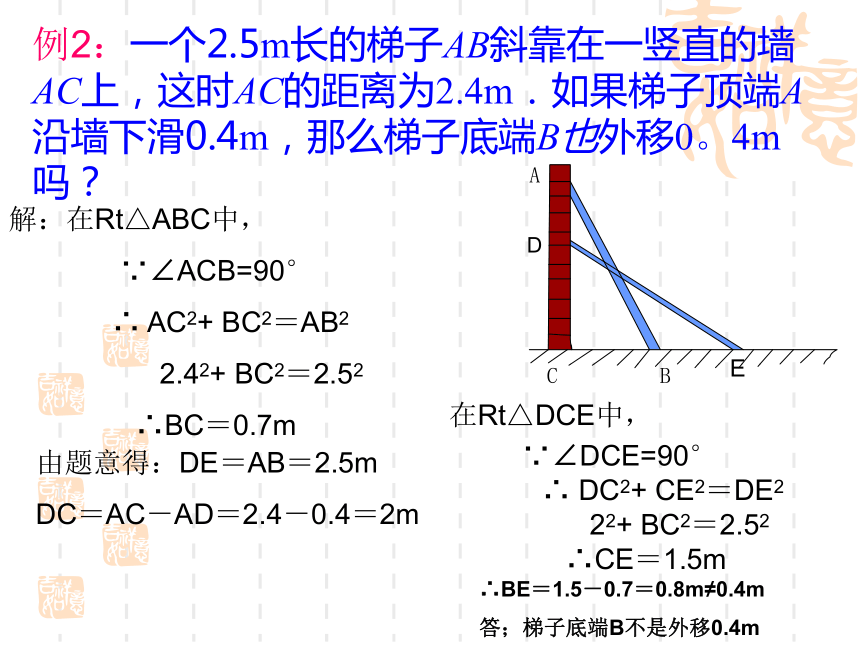
例2:一个2.5m长的梯子AB斜靠在一竖直的墙AC上,这时AC的距离为2.4m.如果梯子顶端A沿墙下滑0.4m,那么梯子底端B也外移0。4m吗?
DE解:在Rt△ABC中,
∵∠ACB=90°
∴ AC2+ BC2=AB2
2.42+ BC2=2.52
∴BC=0.7m由题意得:DE=AB=2.5m
DC=AC-AD=2.4-0.4=2m在Rt△DCE中,∴BE=1.5-0.7=0.8m≠0.4m
答;梯子底端B不是外移0.4m ∵∠DCE=90°
∴ DC2+ CE2=DE2
22+ BC2=2.52
∴CE=1.5m课中探究如图,一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?在Rt△AOB中,
OB2= ,OB= .
在Rt△COD中,
OD2= ,OD= .
BD= .
梯子的顶端沿墙下滑0.5 m,梯子底端外移____变式练习:如图,一个3米长的梯子AB,斜着靠在竖直的墙AO上,这时AO的距离为2.5米.①求梯子的底端B距墙角O多少米?②如果梯子的顶端A沿墙角下滑0.5米至C,请同学们:猜一猜,底端也将滑动0.5米吗?算一算,底端滑动的距离近似值是多少? (结果保留两位小数)尝试应用1、已知如图所示,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得CB=60m,AC=20 m,你能求出A,B两点间的距离吗(结果保留整数)?在RtΔABC中,根据勾股定理:
AB2=BC2-AC2=602-202 = 3200
所以,AC= ≈ 57
A,B两点间的距离约为572、 已知等边三角形ABC的边长是6cm,(1)求高AD的长;(2)S△ABC解:(1)∵△ABC是等边三角形,AD是高在Rt△ABD中,根据勾股定理3:如图,铁路上A,B两点相距25km,C,D为两庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?
x25-x解:设AE= x km,
根据勾股定理,得
AD2+AE2=DE2
BC2+BE2=CE2又 ∵ DE=CE∴ AD2+AE2= BC2+BE2即:152+x2=102+(25-x)2答:E站应建在离A站10km处。∴ X=10则 BE=(25-x)km1510
4:在我国古代数学著作《九章算术》中记载了一道有趣的问题这个问题意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面,问这个水池的深度和这根芦苇的长度各是多少?DABC解:设水池的深度AC为X米,
则芦苇高AD为 (X+1)米.根据题意得:
BC2+AC2=AB2∴52+X2 =(X+1)225+X2=X2+2X+1 X=12 ∴X+1=12+1=13(米)答:水池的深度为12米,芦苇高为13米.5:矩形ABCD如图折叠,使点D落在BC边上的点F处,已知AB=8,BC=10,求折痕AE的长。ABCDFE解:设DE为X,X(8- X)则CE为 (8- X).由题意可知:EF=DE=X,XAF=AD=1010108 ∵∠B=90°
∴ AB2+ BF2=AF282+ BF2=102
∴BF=6∴CF=BC-BF=10-6=464 ∵∠C=90°
∴ CE2+CF2=EF2(8- X)2+42=X264 -16X+X2+16=X280 -16X=016X=80X=56: 如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是( ).
(A)3 (B )√ 5 (C)2 (D)1分析: 由于蚂蚁是沿正方体的外表面爬行的,
故需把正方体展开成平面图形(如图).B当堂达标1.一棵树因雪灾于A处折断,如图所示,测得树梢触地点B到树根C处的距离为4米,∠ABC约45°,树干AC垂直于地面,那么此树在未折断之前的高度约为 米
A. B.4 C. D.以上答案都不对
2.已知直角三角形的两直角边长分别为3cm和5cm,则第三边长为 ____cm第1题图当堂达标3. 有一个边长为1米正方形的洞口,想用一个圆形盖去盖住这个洞口,则圆形盖半径至少为 米.
4.长方形的一边长是5,对角线是13,则另一条边是 .
5.如图所示是一个长方形零件的平面图,尺寸如图所示, 求两孔中心A, B之间的距离.(单位:毫米)第5题图学习体会1.本节课你又那些收获?
2.预习时的疑难问题解决了吗?你还有那些疑惑?
3.你认为本节还有哪些需要注意的地方?布置作业: P教材习题17.1中3、4 、5题
17.1 勾股定理(二)勾股定理:直角三角形两直角边的平方和等于斜边的平方.回 顾 活 动 1如果在Rt△ ABC中,∠C=90°,
那么结论变形c2 = a2 + b2(1)求出下列直角三角形中未知的边.练 习回答:①在解决上述问题时,每个直角三角形需知道几个条件?②直角三角形哪条边最长?(2)在长方形ABCD中,宽AB为1m,长BC为2m ,求AC长.1 m2 m在Rt△ ABC中,∠B=90°,由勾股定理可知:有一个边长为50dm 的正方形洞口,想用一个圆盖去盖住这个洞口,圆的直径至少多长?(结果保留整数)50dmABCD解:∵在Rt△ ABC中,∠B=90°,
AC=BC=50,∴由勾股定理可知:活 动 2
例2:一个2.5m长的梯子AB斜靠在一竖直的墙AC上,这时AC的距离为2.4m.如果梯子顶端A沿墙下滑0.4m,那么梯子底端B也外移0。4m吗?
DE解:在Rt△ABC中,
∵∠ACB=90°
∴ AC2+ BC2=AB2
2.42+ BC2=2.52
∴BC=0.7m由题意得:DE=AB=2.5m
DC=AC-AD=2.4-0.4=2m在Rt△DCE中,∴BE=1.5-0.7=0.8m≠0.4m
答;梯子底端B不是外移0.4m ∵∠DCE=90°
∴ DC2+ CE2=DE2
22+ BC2=2.52
∴CE=1.5m课中探究如图,一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?在Rt△AOB中,
OB2= ,OB= .
在Rt△COD中,
OD2= ,OD= .
BD= .
梯子的顶端沿墙下滑0.5 m,梯子底端外移____变式练习:如图,一个3米长的梯子AB,斜着靠在竖直的墙AO上,这时AO的距离为2.5米.①求梯子的底端B距墙角O多少米?②如果梯子的顶端A沿墙角下滑0.5米至C,请同学们:猜一猜,底端也将滑动0.5米吗?算一算,底端滑动的距离近似值是多少? (结果保留两位小数)尝试应用1、已知如图所示,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得CB=60m,AC=20 m,你能求出A,B两点间的距离吗(结果保留整数)?在RtΔABC中,根据勾股定理:
AB2=BC2-AC2=602-202 = 3200
所以,AC= ≈ 57
A,B两点间的距离约为572、 已知等边三角形ABC的边长是6cm,(1)求高AD的长;(2)S△ABC解:(1)∵△ABC是等边三角形,AD是高在Rt△ABD中,根据勾股定理3:如图,铁路上A,B两点相距25km,C,D为两庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?
x25-x解:设AE= x km,
根据勾股定理,得
AD2+AE2=DE2
BC2+BE2=CE2又 ∵ DE=CE∴ AD2+AE2= BC2+BE2即:152+x2=102+(25-x)2答:E站应建在离A站10km处。∴ X=10则 BE=(25-x)km1510
4:在我国古代数学著作《九章算术》中记载了一道有趣的问题这个问题意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面,问这个水池的深度和这根芦苇的长度各是多少?DABC解:设水池的深度AC为X米,
则芦苇高AD为 (X+1)米.根据题意得:
BC2+AC2=AB2∴52+X2 =(X+1)225+X2=X2+2X+1 X=12 ∴X+1=12+1=13(米)答:水池的深度为12米,芦苇高为13米.5:矩形ABCD如图折叠,使点D落在BC边上的点F处,已知AB=8,BC=10,求折痕AE的长。ABCDFE解:设DE为X,X(8- X)则CE为 (8- X).由题意可知:EF=DE=X,XAF=AD=1010108 ∵∠B=90°
∴ AB2+ BF2=AF282+ BF2=102
∴BF=6∴CF=BC-BF=10-6=464 ∵∠C=90°
∴ CE2+CF2=EF2(8- X)2+42=X264 -16X+X2+16=X280 -16X=016X=80X=56: 如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是( ).
(A)3 (B )√ 5 (C)2 (D)1分析: 由于蚂蚁是沿正方体的外表面爬行的,
故需把正方体展开成平面图形(如图).B当堂达标1.一棵树因雪灾于A处折断,如图所示,测得树梢触地点B到树根C处的距离为4米,∠ABC约45°,树干AC垂直于地面,那么此树在未折断之前的高度约为 米
A. B.4 C. D.以上答案都不对
2.已知直角三角形的两直角边长分别为3cm和5cm,则第三边长为 ____cm第1题图当堂达标3. 有一个边长为1米正方形的洞口,想用一个圆形盖去盖住这个洞口,则圆形盖半径至少为 米.
4.长方形的一边长是5,对角线是13,则另一条边是 .
5.如图所示是一个长方形零件的平面图,尺寸如图所示, 求两孔中心A, B之间的距离.(单位:毫米)第5题图学习体会1.本节课你又那些收获?
2.预习时的疑难问题解决了吗?你还有那些疑惑?
3.你认为本节还有哪些需要注意的地方?布置作业: P教材习题17.1中3、4 、5题
