9.1.2不等式的性质
图片预览



文档简介
课件9张PPT。9.1.2 不等式性质的应用不等式的性质
不等式的性质1:
如果a>b,那么a+c>b+c,a-c>b-c。
不等式的性质2:
如果a>b,并且c>0,那么ac>bc
不等式的性质3:
如果a>b,并且c<0,那么ac 温故而知新确定目标、合作探究1.怎样运用不等式的性质解不等式
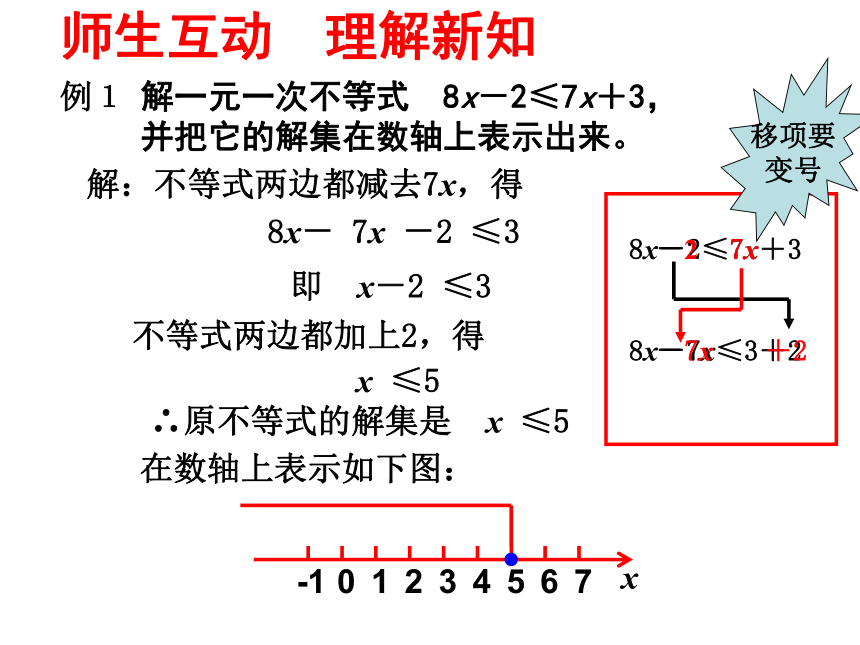
2.解一元一次不等式的依据和步骤是什么?解:不等式两边都减去7x,得 8x- 7x -2 ≤3即 x-2 ≤3不等式两边都加上2,得x ≤5∴原不等式的解集是 x ≤5在数轴上表示如下图:-2+27x-7x移项要
变号解一元一次不等式 8x-2≤7x+3,并把它的解集在数轴上表示出来。例1 师生互动 理解新知例2 解不等式
3(1+x)>2(1+2x)3(1+x)>2(1+2x)解:去括号,得 3+3x>2+4x移项,得 3x-4x> 2-3合并同类项,得 -x>-1系数化为1,得 x<1 写不等式的解集时,要把表示未知数的字母写在不等号的左边。 师生互动 理解新知反馈检测解下列不等式,并在数轴上表示解集:(1)(3)(2)(4)拓展延伸1.不等式 的非正整数解的个数是 2.若不等式 的正整数解是1,2,3,求m的取值范围 知识小结1.解不等式的依据和基本步骤是什么?2.在解不等式时,要注意什么问题?依据:不等式的三个性质基本步骤:去括号、移项、合并同类项、系数化为1(2)系数化为1时,当系数为负数时要改变不等号的方向(1)移项时要改变移动项的符号(3)不等式解集的表示形式为: 或 作 业128页6.
134页练习1.
(1)(2)
不等式的性质1:
如果a>b,那么a+c>b+c,a-c>b-c。
不等式的性质2:
如果a>b,并且c>0,那么ac>bc
不等式的性质3:
如果a>b,并且c<0,那么ac
2.解一元一次不等式的依据和步骤是什么?解:不等式两边都减去7x,得 8x- 7x -2 ≤3即 x-2 ≤3不等式两边都加上2,得x ≤5∴原不等式的解集是 x ≤5在数轴上表示如下图:-2+27x-7x移项要
变号解一元一次不等式 8x-2≤7x+3,并把它的解集在数轴上表示出来。例1 师生互动 理解新知例2 解不等式
3(1+x)>2(1+2x)3(1+x)>2(1+2x)解:去括号,得 3+3x>2+4x移项,得 3x-4x> 2-3合并同类项,得 -x>-1系数化为1,得 x<1 写不等式的解集时,要把表示未知数的字母写在不等号的左边。 师生互动 理解新知反馈检测解下列不等式,并在数轴上表示解集:(1)(3)(2)(4)拓展延伸1.不等式 的非正整数解的个数是 2.若不等式 的正整数解是1,2,3,求m的取值范围 知识小结1.解不等式的依据和基本步骤是什么?2.在解不等式时,要注意什么问题?依据:不等式的三个性质基本步骤:去括号、移项、合并同类项、系数化为1(2)系数化为1时,当系数为负数时要改变不等号的方向(1)移项时要改变移动项的符号(3)不等式解集的表示形式为: 或 作 业128页6.
134页练习1.
(1)(2)
