人教A版(2019)必修第一册 4.2.2对数函数的图象和性质(第二课时)课件(共16张PPT)
文档属性
| 名称 | 人教A版(2019)必修第一册 4.2.2对数函数的图象和性质(第二课时)课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 685.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-10 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
4.2.2对数函数的图象和性质
(第二课时)
温故知新
1. 说一说对数函数的概念
2. 对数函数的图象及性质
题型一 与对数函数有关的函数图象恒过定点问题
1.令真数为1
2.求x
3.代入求y
4.写出点(x,y)
题型二 解对数不等式
题型三 含对数式的函数的定义域、值域
题型四 已知与对数函数有关的函数的最值,求参数的取值
方法小结 如果底数中参数的取值不确定时,要对底数的范围进行分类讨论,以确定该函数的单调性,则可利用最值
题型五 对数型函数的奇偶性问题
题型六 对数型函数的单调性问题
题型七 与对数函数有关的函数图象及其应用
题型八 反函数
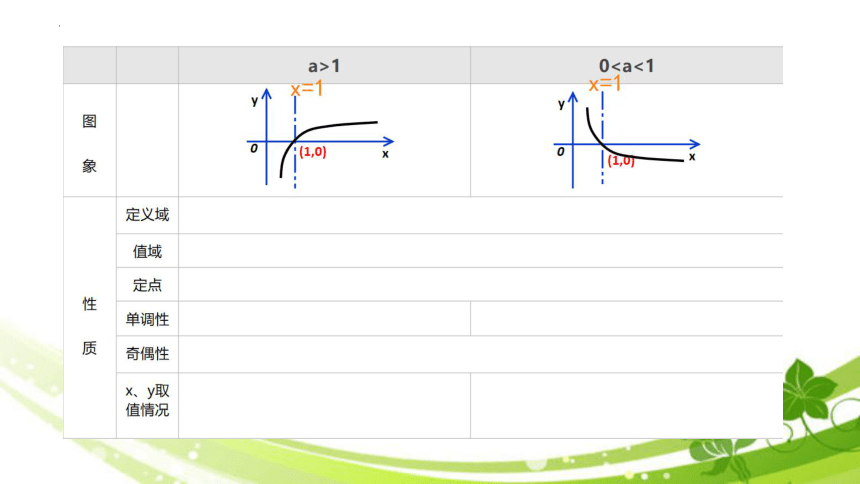
a>1
0X二1
图
0
象
定义域
值域
定点
性
单调性
质
奇偶性
x、y取
值情况
典例1己知函数f(x)=lnx,若f八(x-1)<1,则实数
x的取值范围是()
A.(-c,e+1)
B.(0,+c)
C.(1,e+1)
D.(e+1,+c)
典例2
已知函数/(x)=log(1-)+loga(x+3)(a>0且a≠1)
①求函数f(x)的定义域和值域.
②若函数f八x)有最小值为-2,求的值.
典例3函数y=g(xhVx2+1)是()
A.偶函数
B.奇函数
C.既是奇函数又是偶函数
D.既不是奇函数又不是偶函数
典例4函数f(x)=gx2的单调递减区间是()
A.(-0,0)
B.(-0,1)
C.(1,,+∝)
D.(0,+c)
求复合函数形如y=logf八x)(a>0且a≠1)的单调性步骤如下:
①求函数的定义域
②令t=f(x),则y=loga1
③分别求函数t=f(x)和函数y=log在定义域内的单调性
④利用口诀“同增异减”最后得出原函数的单调性,
即内外层单调性相同,则原函数就是增函数,
内外层单调性相反,则原函数就是减函数
定义域问题
值域问题
换元法求值域
小结
与对数函数有关的函数应用
单调性应用°
对数型复合函数的单调性
奇偶性应用
4.2.2对数函数的图象和性质
(第二课时)
温故知新
1. 说一说对数函数的概念
2. 对数函数的图象及性质
题型一 与对数函数有关的函数图象恒过定点问题
1.令真数为1
2.求x
3.代入求y
4.写出点(x,y)
题型二 解对数不等式
题型三 含对数式的函数的定义域、值域
题型四 已知与对数函数有关的函数的最值,求参数的取值
方法小结 如果底数中参数的取值不确定时,要对底数的范围进行分类讨论,以确定该函数的单调性,则可利用最值
题型五 对数型函数的奇偶性问题
题型六 对数型函数的单调性问题
题型七 与对数函数有关的函数图象及其应用
题型八 反函数
a>1
0
图
0
象
定义域
值域
定点
性
单调性
质
奇偶性
x、y取
值情况
典例1己知函数f(x)=lnx,若f八(x-1)<1,则实数
x的取值范围是()
A.(-c,e+1)
B.(0,+c)
C.(1,e+1)
D.(e+1,+c)
典例2
已知函数/(x)=log(1-)+loga(x+3)(a>0且a≠1)
①求函数f(x)的定义域和值域.
②若函数f八x)有最小值为-2,求的值.
典例3函数y=g(xhVx2+1)是()
A.偶函数
B.奇函数
C.既是奇函数又是偶函数
D.既不是奇函数又不是偶函数
典例4函数f(x)=gx2的单调递减区间是()
A.(-0,0)
B.(-0,1)
C.(1,,+∝)
D.(0,+c)
求复合函数形如y=logf八x)(a>0且a≠1)的单调性步骤如下:
①求函数的定义域
②令t=f(x),则y=loga1
③分别求函数t=f(x)和函数y=log在定义域内的单调性
④利用口诀“同增异减”最后得出原函数的单调性,
即内外层单调性相同,则原函数就是增函数,
内外层单调性相反,则原函数就是减函数
定义域问题
值域问题
换元法求值域
小结
与对数函数有关的函数应用
单调性应用°
对数型复合函数的单调性
奇偶性应用
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
