17.2勾股定理的逆定理课件
文档属性
| 名称 | 17.2勾股定理的逆定理课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-24 00:00:00 | ||
图片预览





文档简介
课件26张PPT。在数学的天地里,重要的不是我们知道
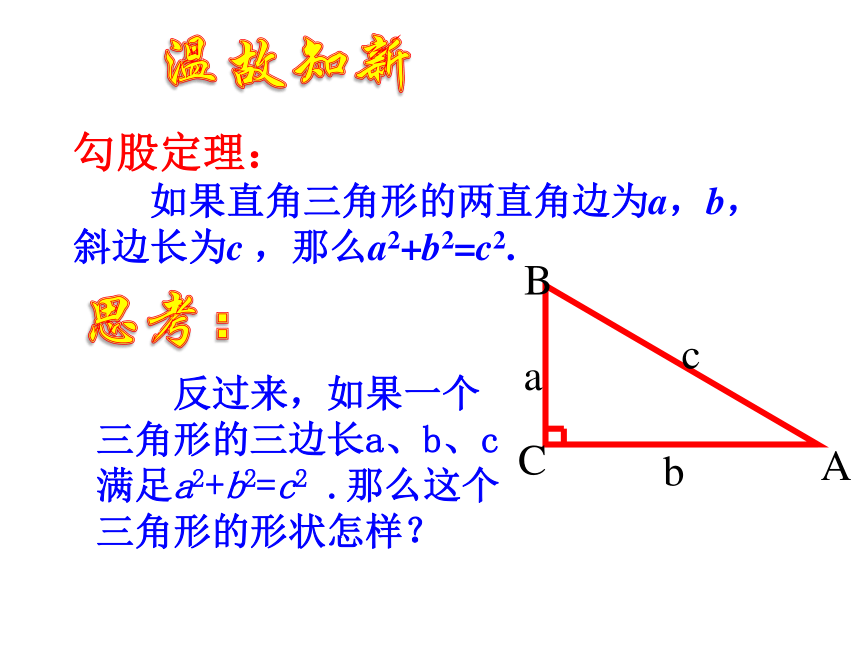
什么,而是我们怎么知道什么。 —毕达哥拉斯 17.2 勾股定理的逆定理沈 习 兵横山中学温故知新勾股定理:
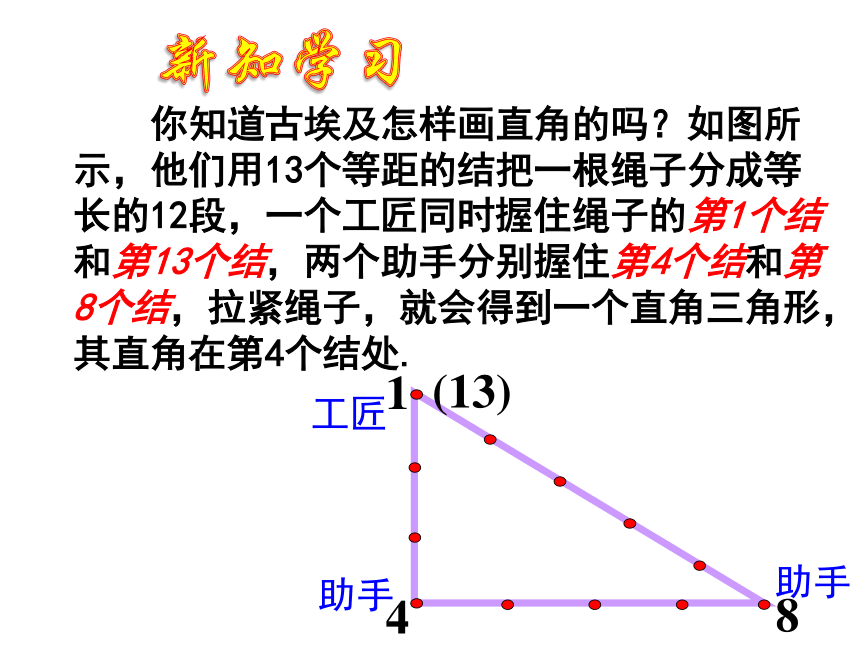
如果直角三角形的两直角边为a,b,斜边长为c ,那么a2+b2=c2. 反过来,如果一个三角形的三边长a、b、c满足a2+b2=c2 .那么这个三角形的形状怎样?思考: 你知道古埃及怎样画直角的吗?如图所示,他们用13个等距的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处.新知学习工匠助手助手
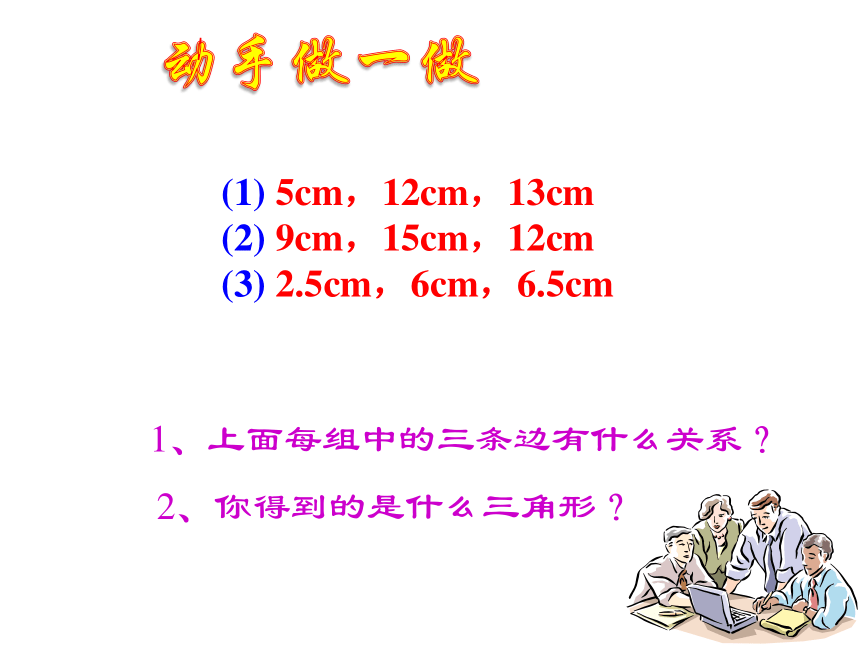
(1) 5cm,12cm,13cm
(2) 9cm,15cm,12cm
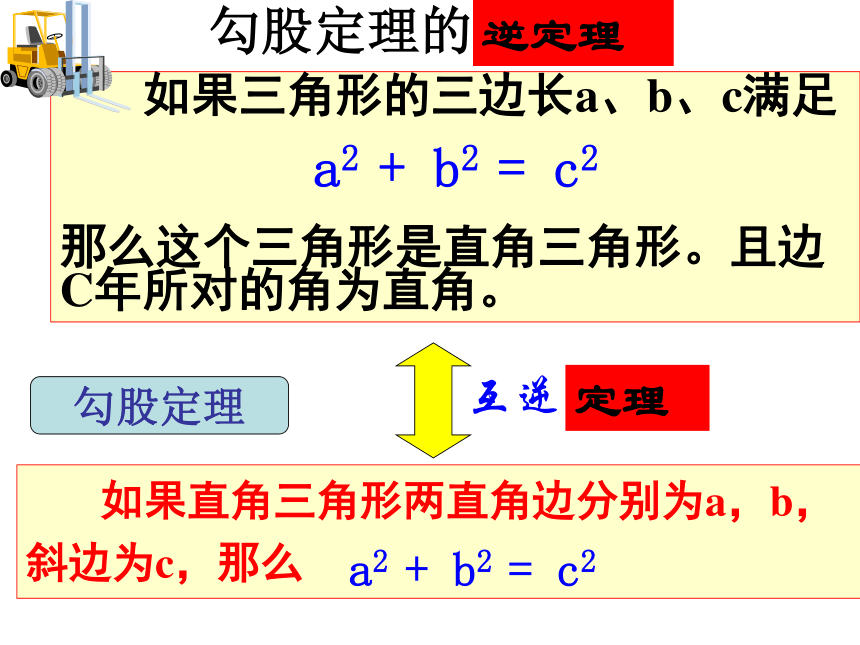
(3) 2.5cm,6cm,6.5cm1、上面每组中的三条边有什么关系?动手做一做2、你得到的是什么三角形?勾股定理的逆命题勾股定理互逆命题互逆命题:
两个命题中, 如果第一个命题的题设是第二个命题的结论, 而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题.
如果把其中一个叫做原命题, 那么另一个叫做它的逆命题.
互逆定理:
如果一个定理的逆命题经过证明是真命题, 那么它也是一个定理, 这两个定理叫做互逆定理, 其中一个叫做另一个的逆定理.
驶向胜利的彼岸定理与逆定理我们已经学习了一些互逆的定理,如:
勾股定理及其逆定理,
两直线平行,内错角相等;内错角相等,两直线平行.想一想:
互逆命题与互逆定理有何关系?(1)两条直线平行,内错角相等.
(2)如果两个实数相等,那么它们的平方相等.
(3)如果两个实数相等,那么它们的绝对值相等.
(4)全等三角形的对应角相等.说出下列命题的逆命题.这些命题的逆命题成立吗?逆命题: 内错角相等,两条直线平行. 成立逆命题:如果两个实数的平方相等,那么这两个实数相等. 不成立逆命题:如果两个实数的绝对值相等,那么这两个实数相等. 不成立逆命题:对应角相等的两个三角形是全等三角形. 不成立感悟: 原命题成立时, 逆命题有时成立, 有时不成立一个命题是真命题,它逆命题却不一定是真命题.勾股定理的逆命题勾股定理互逆命题逆定理定理∵ ∠ C’=900∴ A’B’2= a2+b2∵ a2+b2=c2∴ A’B’ 2=c2∴ A’B’ =c∵ 边长取正值∴ △ ABC ≌△ A’B’C’(SSS)∴ ∠ C= ∠ C’(全等三角形对应角相等)∴ ∠C= 900已知:在△ABC中,AB=c BC=a CA=b 且a2+b2=c2求证:△ ABC是直角三角形证明:画一个△A’B’C’,使∠ C’=900,B’C’=a, C’A’=b在△ ABC和△ A’B’C’中∴ △ ABC是直角三角形(直角三角形的定义)勾股定理的逆命题证明例1 判断由a、b、c组成的三角形是不是直角三角形:
(1) a=15 , b =8 , c=17(2) a=13 , b =15 , c=14分析:由勾股定理的逆定理,判断三角形是不是直角三角形,只要看两条较小边的平方和是否等于最大边的平方。解:∵152+82=225+64=289
172=289
∴ 152+82=172
∴这个三角形是直角三角形 下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?(1) a=25 b=20 c=15 ____ _____ ;(2) a=13 b=14 c=15 ____ _____ ;(4) a:b: c=3:4:5 _____ _____ ;是是不是 是∠ A=900∠ B=900∠ C=900(3) a=1 b=2 c= ____ _____ ; 像25,20,15,能够成为直角三角形三条边长的三个正整数,称为勾股数.例1: “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里。它们离开港口一个半小时后相距30海里。如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
随堂练习:
1、将下列长度的三木棒首尾顺次连接,能组成直角三角形的是( )
(A)1, 2, 3 (B)4, 6, 8 (C)5, 5, 4 (D)15,12, 9 2、如果线段a、b、c能组成直角三角形, 则它们的比可能是( )
(A)3:4:7; (B)5:12:13;
(C)1:2:4; (D)1:3:5.D B三角形的三边分别是a、b、c, 且满足
(a+b)2-c2=2ab, 则此三角形是:( )
A. 直角三角形; B. 是锐角三角形;
是钝角三角形; D. 是等腰直角三角形.4、一个零件的形状如下图所示,按规定这个零件
中∠A和∠DBC都应为直角.工人师傅量出了这个
零件各边尺寸,那么这个零件符合要求吗? 此时四边形ABCD
的面积是多少?5、 已知a、b、c为△ABC的三边,且 满足
a2+b2+c2+338=10a+24b+26c.
试判断△ABC的形状.6、△ABC三边a,b,c为边向外作正方形,正三角形,以三边为直径作半圆,若S1+S2=S3成立,则是直角三角形吗?
ACabcS1S2S3BABCabcS1S2S3活动2:范例讲解例7:判断由线段a、b、c组成的三角形是不是直角三角形:
(1)a=15,b=8,c=17;
(2)a=m2-n2,b=m2+n2,c=2mn(m>n,m、n是正整数)解;(1)∵a2 = 225,
b2 = 64, c2 = 289
又∵ 225 + 64 = 289
∴ a2 + b2 = c2
即: 三角形是直角三角形(2)∵a2 = (m2 - n2 )2 = m4 - 2m2n2 + n4, b2 = (m2 + n2 )2 = m4 + 2m2n2 + n4,
c2 = (2mn )2 = 4m2n2
又∵m4 - 2m2n2 + n4 + 4m2n2
= m4 + 2m2n2 + n4
∴ a2 + c2 = b2
即: 三角形是直角三角形知识运用:8如图:在正方形ABCD中,E是BC的中点,F是CD上一点,
且CF= CD.猜想△AEF的形状,并证明你的结论.解: △AEF是直角三角形;
理由:设正方形ABCD的边长是a,则:9.台风是一种自然灾害,它以台风中心为圆心,在周围数十千米的范围内形成气旋风暴,有极强的破坏力。如图所示,据气象部门报道:距沿海城市A的正南方向220千米B处有一个台风中心,其中心最大风力12级,距离台风中心20千米,风力会减弱一级。该台风正以15km/h的速度沿北偏东30°方向往C处移动,且台风中心风力不变,若城市所受风力达到或超过四级,则称受到台风影响。
(1)该城市是否会受到此次台风的影响?请说明理由。
(2)若受到影响,那么台风影响该城市的持续时间为多长?
(3)该城市受到台风影响的最大风力为几级?
思考题:10.已知a.b.c为△ABC的三边,且满足 a2c2 – b2c2=a4 – b4,试判断△ABC的形状.
解 ∵ a2c2- b2c2 = a4 – b4 (1)
∴ c2(a2 – b2) = (a2+ b2) (a2- b2) (2)
∴ c2 = a2 + b2 (3)
∴ △ABC是直角三角形
问: (1) 上述解题过程,从哪一步开始出现错误?请写出该步的代号___
(2) 错误原因是_________
(3) 本题正确的结论是________3a2- b2可能是0直角三角形或等腰三角形11、如图:在Δ ABC中,AB=13㎝,BC=10㎝,BC边上的中线AD=12㎝,求证:AB=AC。证明:∵AD是BC边上的中线,
∴BD=CD=1/2BC=5㎝
∵在△ABD中,AB=13,BD=5,AD=12
∴ BD2+AD2=52+122=169=AB2
∴ △ABD是直角三角形。
∴ △ACD也是直角三角形。
根据勾股定理得到:∴AB=AC=13㎝满足 的三个 ,称为勾股数。正整数你能写出常用的勾股数吗?3,4,5; 5,12,13;
6,8,10; 7,24,25;
8,15,17 ;9,40,41勾股小常识:
(1) a2+b2 =c2,满足(a,b,c)=1则a,b,c,为基本勾数如:3、4、5; 5、12、 13; 7、24、25……
(2)如果a,b,c是一组勾股数,则ka、kb、kc(k为正整数)也是一组勾股数,如:6、8、10;9、12、15……
(3)若a,b,c是一组基本的勾股数,则a、b、c不能同时为奇数
(4)一组勾股数中必有一个数是5倍数
(5) 2mn,m2-n2,m2+n2为勾股数组,m>n﹥0,m,n一奇一偶
探索猜想归纳验证应用拓展学习收获判定一个三角形是直角三角形的方法有一个角是直角的三角形是直角三角形.角:边:如果三角形的三边长a,b,c满足 a2+b2=c2,那么这个三角形是直角三角形再 见
什么,而是我们怎么知道什么。 —毕达哥拉斯 17.2 勾股定理的逆定理沈 习 兵横山中学温故知新勾股定理:
如果直角三角形的两直角边为a,b,斜边长为c ,那么a2+b2=c2. 反过来,如果一个三角形的三边长a、b、c满足a2+b2=c2 .那么这个三角形的形状怎样?思考: 你知道古埃及怎样画直角的吗?如图所示,他们用13个等距的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处.新知学习工匠助手助手
(1) 5cm,12cm,13cm
(2) 9cm,15cm,12cm
(3) 2.5cm,6cm,6.5cm1、上面每组中的三条边有什么关系?动手做一做2、你得到的是什么三角形?勾股定理的逆命题勾股定理互逆命题互逆命题:
两个命题中, 如果第一个命题的题设是第二个命题的结论, 而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题.
如果把其中一个叫做原命题, 那么另一个叫做它的逆命题.
互逆定理:
如果一个定理的逆命题经过证明是真命题, 那么它也是一个定理, 这两个定理叫做互逆定理, 其中一个叫做另一个的逆定理.
驶向胜利的彼岸定理与逆定理我们已经学习了一些互逆的定理,如:
勾股定理及其逆定理,
两直线平行,内错角相等;内错角相等,两直线平行.想一想:
互逆命题与互逆定理有何关系?(1)两条直线平行,内错角相等.
(2)如果两个实数相等,那么它们的平方相等.
(3)如果两个实数相等,那么它们的绝对值相等.
(4)全等三角形的对应角相等.说出下列命题的逆命题.这些命题的逆命题成立吗?逆命题: 内错角相等,两条直线平行. 成立逆命题:如果两个实数的平方相等,那么这两个实数相等. 不成立逆命题:如果两个实数的绝对值相等,那么这两个实数相等. 不成立逆命题:对应角相等的两个三角形是全等三角形. 不成立感悟: 原命题成立时, 逆命题有时成立, 有时不成立一个命题是真命题,它逆命题却不一定是真命题.勾股定理的逆命题勾股定理互逆命题逆定理定理∵ ∠ C’=900∴ A’B’2= a2+b2∵ a2+b2=c2∴ A’B’ 2=c2∴ A’B’ =c∵ 边长取正值∴ △ ABC ≌△ A’B’C’(SSS)∴ ∠ C= ∠ C’(全等三角形对应角相等)∴ ∠C= 900已知:在△ABC中,AB=c BC=a CA=b 且a2+b2=c2求证:△ ABC是直角三角形证明:画一个△A’B’C’,使∠ C’=900,B’C’=a, C’A’=b在△ ABC和△ A’B’C’中∴ △ ABC是直角三角形(直角三角形的定义)勾股定理的逆命题证明例1 判断由a、b、c组成的三角形是不是直角三角形:
(1) a=15 , b =8 , c=17(2) a=13 , b =15 , c=14分析:由勾股定理的逆定理,判断三角形是不是直角三角形,只要看两条较小边的平方和是否等于最大边的平方。解:∵152+82=225+64=289
172=289
∴ 152+82=172
∴这个三角形是直角三角形 下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?(1) a=25 b=20 c=15 ____ _____ ;(2) a=13 b=14 c=15 ____ _____ ;(4) a:b: c=3:4:5 _____ _____ ;是是不是 是∠ A=900∠ B=900∠ C=900(3) a=1 b=2 c= ____ _____ ; 像25,20,15,能够成为直角三角形三条边长的三个正整数,称为勾股数.例1: “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里。它们离开港口一个半小时后相距30海里。如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
随堂练习:
1、将下列长度的三木棒首尾顺次连接,能组成直角三角形的是( )
(A)1, 2, 3 (B)4, 6, 8 (C)5, 5, 4 (D)15,12, 9 2、如果线段a、b、c能组成直角三角形, 则它们的比可能是( )
(A)3:4:7; (B)5:12:13;
(C)1:2:4; (D)1:3:5.D B三角形的三边分别是a、b、c, 且满足
(a+b)2-c2=2ab, 则此三角形是:( )
A. 直角三角形; B. 是锐角三角形;
是钝角三角形; D. 是等腰直角三角形.4、一个零件的形状如下图所示,按规定这个零件
中∠A和∠DBC都应为直角.工人师傅量出了这个
零件各边尺寸,那么这个零件符合要求吗? 此时四边形ABCD
的面积是多少?5、 已知a、b、c为△ABC的三边,且 满足
a2+b2+c2+338=10a+24b+26c.
试判断△ABC的形状.6、△ABC三边a,b,c为边向外作正方形,正三角形,以三边为直径作半圆,若S1+S2=S3成立,则是直角三角形吗?
ACabcS1S2S3BABCabcS1S2S3活动2:范例讲解例7:判断由线段a、b、c组成的三角形是不是直角三角形:
(1)a=15,b=8,c=17;
(2)a=m2-n2,b=m2+n2,c=2mn(m>n,m、n是正整数)解;(1)∵a2 = 225,
b2 = 64, c2 = 289
又∵ 225 + 64 = 289
∴ a2 + b2 = c2
即: 三角形是直角三角形(2)∵a2 = (m2 - n2 )2 = m4 - 2m2n2 + n4, b2 = (m2 + n2 )2 = m4 + 2m2n2 + n4,
c2 = (2mn )2 = 4m2n2
又∵m4 - 2m2n2 + n4 + 4m2n2
= m4 + 2m2n2 + n4
∴ a2 + c2 = b2
即: 三角形是直角三角形知识运用:8如图:在正方形ABCD中,E是BC的中点,F是CD上一点,
且CF= CD.猜想△AEF的形状,并证明你的结论.解: △AEF是直角三角形;
理由:设正方形ABCD的边长是a,则:9.台风是一种自然灾害,它以台风中心为圆心,在周围数十千米的范围内形成气旋风暴,有极强的破坏力。如图所示,据气象部门报道:距沿海城市A的正南方向220千米B处有一个台风中心,其中心最大风力12级,距离台风中心20千米,风力会减弱一级。该台风正以15km/h的速度沿北偏东30°方向往C处移动,且台风中心风力不变,若城市所受风力达到或超过四级,则称受到台风影响。
(1)该城市是否会受到此次台风的影响?请说明理由。
(2)若受到影响,那么台风影响该城市的持续时间为多长?
(3)该城市受到台风影响的最大风力为几级?
思考题:10.已知a.b.c为△ABC的三边,且满足 a2c2 – b2c2=a4 – b4,试判断△ABC的形状.
解 ∵ a2c2- b2c2 = a4 – b4 (1)
∴ c2(a2 – b2) = (a2+ b2) (a2- b2) (2)
∴ c2 = a2 + b2 (3)
∴ △ABC是直角三角形
问: (1) 上述解题过程,从哪一步开始出现错误?请写出该步的代号___
(2) 错误原因是_________
(3) 本题正确的结论是________3a2- b2可能是0直角三角形或等腰三角形11、如图:在Δ ABC中,AB=13㎝,BC=10㎝,BC边上的中线AD=12㎝,求证:AB=AC。证明:∵AD是BC边上的中线,
∴BD=CD=1/2BC=5㎝
∵在△ABD中,AB=13,BD=5,AD=12
∴ BD2+AD2=52+122=169=AB2
∴ △ABD是直角三角形。
∴ △ACD也是直角三角形。
根据勾股定理得到:∴AB=AC=13㎝满足 的三个 ,称为勾股数。正整数你能写出常用的勾股数吗?3,4,5; 5,12,13;
6,8,10; 7,24,25;
8,15,17 ;9,40,41勾股小常识:
(1) a2+b2 =c2,满足(a,b,c)=1则a,b,c,为基本勾数如:3、4、5; 5、12、 13; 7、24、25……
(2)如果a,b,c是一组勾股数,则ka、kb、kc(k为正整数)也是一组勾股数,如:6、8、10;9、12、15……
(3)若a,b,c是一组基本的勾股数,则a、b、c不能同时为奇数
(4)一组勾股数中必有一个数是5倍数
(5) 2mn,m2-n2,m2+n2为勾股数组,m>n﹥0,m,n一奇一偶
探索猜想归纳验证应用拓展学习收获判定一个三角形是直角三角形的方法有一个角是直角的三角形是直角三角形.角:边:如果三角形的三边长a,b,c满足 a2+b2=c2,那么这个三角形是直角三角形再 见
