青岛版七年级上册数学5.3代数式的值 课件(共16张PPT)
文档属性
| 名称 | 青岛版七年级上册数学5.3代数式的值 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 161.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-11 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
5.3 代 数 式 的 值
学习目标
1.我能了解代数式的值的意义,会求代数式的值;
2.我会探索具体问题中的数量关系,用代数式表示,
通过求代数式的值,感受模型思想;
3.能用数学知识解决实际问题,提高学习数学的兴趣。
一般地,用 代替代数式里的_____,按照代数式____________计算出的 ,叫做_________。
字母
指明的运算
代数式的值
数
结果
合作探究一
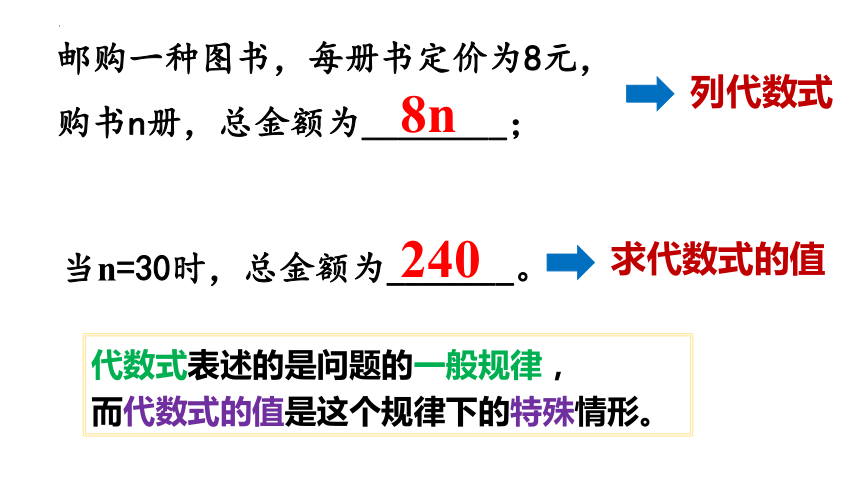
邮购一种图书,每册书定价为8元,购书n册,总金额为________;
8n
列代数式
当n=30时,总金额为_______。
240
求代数式的值
代数式表述的是问题的一般规律,
而代数式的值是这个规律下的特殊情形。
一般地,用 代替代数式里的_____,按照代数式____________计算出的 ,叫做_____________。
字母
指明的运算
代数式的值
数
结果
代数式的值
用数代替代数式里的字母,按照代数式指明的运算计算出的结果,叫做代数式的值。
代数式的值
时代中学八年级有x名同学参加植树,平均每人植树3棵;七年级有y名同学参加参加植树,平均每人植树2棵。
①该校七、八年级同学共植树多少棵?
②如果x=98,y=102,那么这个学校七、八年共植树木多少棵?
解:①八年级同学共植树____棵七年级同学共植树____棵, 该校七年级八年级共植树_______ 棵。
②在代数式3x+2y中,分别用98代替x,用102代替y,
得到
3x
2y
3x+2y
3×98+2×102=498(棵)
合作探究二
温馨提示
1.用具体数值代替代数式中字母进行计算必须按照代数式指明的运算顺序;
2.将数值代替字母时注意一些运算符号和括号的
添加;
3. 将数代入字母时要注意对应代入;
4.注意书写格式:解 :当……
原式=……
1、已知X=3,y=-2,求代数式xy-x2的值。
解:当X=3,y=-2时
xy-x2=3×(-2)-32
=-6-6
=-12
步骤:一代 ; 二算
当堂检测
2、若a2=1,则3a2=______.
变式一:若a2+a=1,则3(a2+a)=________;
变式二:若a2+a=1,则3a2+3a-5=_______;
变式三:若a2+a+3=0,则3a2+3a-5=______.
3
3
-2
-14
整体代入思想
3、当a=2,b=-1时,求下列代数式的值
3a+5 a2+b2+2ab (a+b)2
解:当a=2,b=-1时,
原式=3 2+5
=6+5
=11
解:当a=2,b=-1时,
原式 =22+(-1)2+2×2×(-1)
=4+1-4
=1
解:当a=2,b=-1时,
原式 =(2-1)2
=1
4、若a与b互为相反数,c与d互为倒数,且|m+2|+(n-3)2=0,求a+b-cd-m+n的值.
解:由题意知:
a+b=0,cd=1
m+2=0,n-3=0
∴m=-2,n=3
原式=0-1-(-2)+3
=4
5、 2x2+3x-5的值是8,求代 数式4x2+6x-15的值。
解:当2x2+3x-5=8时
原式=2×(2x2+3x-5)-5
=2×8-5
=16-5
= 11
5、 2x2+3x-5的值是8,求代数式4x2+6x-15的值。
解:当2x2+3x-5=8时
原式=2×(2x2+3x-5)-5
=2×8-5
=16-5
= 11
解:∵2x2+3x-5=8
∴2x2+3x=13
∴原式=2×(2x2+3x)-15
=2×13-15
=26-15
=11
6、天泉村去年的小麦产量为a吨,今年比去年增加了10%,今年的小麦总产量是多少吨?如果去年的小麦总产量是480吨,今年的小麦总产量是多少吨?
解:今年小麦总产量:a(1+10%)=1.1a
当a=480时,1.1a=1.1×480=528(吨)
答:今年的小麦总产量是528吨
小结
1、本节课主要学习了代数式的值;
2、知道求代数式的值的方法:一代,二算, 另外要注意规范解题格式;
3、代数式的变形求值问题。
5.3 代 数 式 的 值
学习目标
1.我能了解代数式的值的意义,会求代数式的值;
2.我会探索具体问题中的数量关系,用代数式表示,
通过求代数式的值,感受模型思想;
3.能用数学知识解决实际问题,提高学习数学的兴趣。
一般地,用 代替代数式里的_____,按照代数式____________计算出的 ,叫做_________。
字母
指明的运算
代数式的值
数
结果
合作探究一
邮购一种图书,每册书定价为8元,购书n册,总金额为________;
8n
列代数式
当n=30时,总金额为_______。
240
求代数式的值
代数式表述的是问题的一般规律,
而代数式的值是这个规律下的特殊情形。
一般地,用 代替代数式里的_____,按照代数式____________计算出的 ,叫做_____________。
字母
指明的运算
代数式的值
数
结果
代数式的值
用数代替代数式里的字母,按照代数式指明的运算计算出的结果,叫做代数式的值。
代数式的值
时代中学八年级有x名同学参加植树,平均每人植树3棵;七年级有y名同学参加参加植树,平均每人植树2棵。
①该校七、八年级同学共植树多少棵?
②如果x=98,y=102,那么这个学校七、八年共植树木多少棵?
解:①八年级同学共植树____棵七年级同学共植树____棵, 该校七年级八年级共植树_______ 棵。
②在代数式3x+2y中,分别用98代替x,用102代替y,
得到
3x
2y
3x+2y
3×98+2×102=498(棵)
合作探究二
温馨提示
1.用具体数值代替代数式中字母进行计算必须按照代数式指明的运算顺序;
2.将数值代替字母时注意一些运算符号和括号的
添加;
3. 将数代入字母时要注意对应代入;
4.注意书写格式:解 :当……
原式=……
1、已知X=3,y=-2,求代数式xy-x2的值。
解:当X=3,y=-2时
xy-x2=3×(-2)-32
=-6-6
=-12
步骤:一代 ; 二算
当堂检测
2、若a2=1,则3a2=______.
变式一:若a2+a=1,则3(a2+a)=________;
变式二:若a2+a=1,则3a2+3a-5=_______;
变式三:若a2+a+3=0,则3a2+3a-5=______.
3
3
-2
-14
整体代入思想
3、当a=2,b=-1时,求下列代数式的值
3a+5 a2+b2+2ab (a+b)2
解:当a=2,b=-1时,
原式=3 2+5
=6+5
=11
解:当a=2,b=-1时,
原式 =22+(-1)2+2×2×(-1)
=4+1-4
=1
解:当a=2,b=-1时,
原式 =(2-1)2
=1
4、若a与b互为相反数,c与d互为倒数,且|m+2|+(n-3)2=0,求a+b-cd-m+n的值.
解:由题意知:
a+b=0,cd=1
m+2=0,n-3=0
∴m=-2,n=3
原式=0-1-(-2)+3
=4
5、 2x2+3x-5的值是8,求代 数式4x2+6x-15的值。
解:当2x2+3x-5=8时
原式=2×(2x2+3x-5)-5
=2×8-5
=16-5
= 11
5、 2x2+3x-5的值是8,求代数式4x2+6x-15的值。
解:当2x2+3x-5=8时
原式=2×(2x2+3x-5)-5
=2×8-5
=16-5
= 11
解:∵2x2+3x-5=8
∴2x2+3x=13
∴原式=2×(2x2+3x)-15
=2×13-15
=26-15
=11
6、天泉村去年的小麦产量为a吨,今年比去年增加了10%,今年的小麦总产量是多少吨?如果去年的小麦总产量是480吨,今年的小麦总产量是多少吨?
解:今年小麦总产量:a(1+10%)=1.1a
当a=480时,1.1a=1.1×480=528(吨)
答:今年的小麦总产量是528吨
小结
1、本节课主要学习了代数式的值;
2、知道求代数式的值的方法:一代,二算, 另外要注意规范解题格式;
3、代数式的变形求值问题。
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
