福建省厦门市杏南中学2023-2024学年高二上学期11月期中阶段测试数学试题(PDF版含答案)
文档属性
| 名称 | 福建省厦门市杏南中学2023-2024学年高二上学期11月期中阶段测试数学试题(PDF版含答案) |

|
|
| 格式 | |||
| 文件大小 | 611.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-10 00:00:00 | ||
图片预览




文档简介
厦门市杏南中学 2023-2024 学年学年上学期期中阶段测试卷
高二年 数学
作答时间:120 分钟
一、单选题:本题共 8小题,每小题 5分,共 40分。在每小题给出的四个选项中,只有一
项是符合题目要求的。
1. 直线 3x y 1 0的倾斜角是 ( )
A. 30 B. 60 C. 120 D. 150
2. 直线 l1 :ax 2y 3 0 与直线 l2 : x (a 1)y 2 0互相垂直,则 a ( )
A. 0 B. 1 C. 2 D. 1
x2 y2
3. 已知椭圆 C: 1的左、右焦点分别为 F1,F2,且 PF1 2,则 PF2 ( )9 7
A. 4 B. 6 C. 2 7 2 D. 2 2 2
4. 已知直线 l : x 2y 1 0 C : x2 y2经过圆 Dx 2y 3 0的圆心,则D ( )
A. 6 B. 2 C. 2 D. 6
5. 如图,在正方体 ABCD A1B1C1D1中,M是 AB的中点,则异面直线DB1,CM 所成
角的余弦值是 ( )
2 15
A. B.
6 5
2 15
C. D.
15 15
6. 2 2已知圆C1 : x y 4x 2y 4 0 C (: x 1)
2
与圆 2 (y 3)
2 4,圆C1与圆C2的位
置关系是 ( )
A. 外离 B. 外切 C. 相交 D. 内切
7. x2 y2在圆 9的上任取一点 P,过 P作 x轴的垂线段 PD,垂足为D,并延长DP至M ,
PM 1使得 DP ,则点M 的轨迹方程是 ( )
3
x2 y2 x2 y2 x2 y2 x2 y2
A. 1 B. 1 C. 1 D. 1
9 4 16 9 9 16 3 4
x2 y2
8.已知椭圆 C: 2 2 1(a b 0)a b 的右焦点为
F2,O 为坐标原点为,M 为 y 轴上一点,
点 A是直线MF2与椭圆 C的一个交点,且 OA OF2 2OM ,则椭圆 C的离心率是( )
1 2 5 5
A. B. C. D.
3 5 5 3
二、选择题多选题:本题共 4小题,每小题 5分,共 20分。在每小题给出的四个选项中,
有多个选项符合题目要求,全部选对的得 5分,选对但不全的得 2分,有选错的得 0分。
9. 已知直线 l : 4x 3y 2 0,下列说法正确的是 ( )
1
A. 直线 l经过点 P(1,2) B. 直线 l与坐标轴围成的三角形面积是
6
C. 直线 l与直线8x 6y 7 0 2的距离是 1 D. 直线 l与圆(x 1) (y 3)2 9相切
(高二数学试卷 第 1 页,共 4 页)
{#{QQABDYyUogCgQAJAAQhCEwGgCACQkACCCAoGhAAMIAIBQRFABAA=}#}
10. 2已知双曲线C : x y2 4,下列说法正确的是 ( )
x2
A. 双曲线C的实轴长是 2 B. 2双曲线C与椭圆 y 1有相同的焦点
9
C. 双曲线C的离心率 e 2 D. 直线 y 2x与双曲线C没有公共点
x2 y2
11. 已知椭圆 C: 19 4 的左、右焦点分别为 F1,F2,点 M 与焦点不重合。若 M 关于
F1,F2对称的点分别为 A,B,线段 MN 的中点 P 在椭圆 C 上,则 ( )
A. 焦点分别为 F1,F2的坐标分别为( 5,0)(, 5,0)
B. 点 N 一定在椭圆 C 外
2
C. M O N x y
2
当点 与原点 重合时,点 的轨迹方程是 1
36 16
D. NA NB 12
12.已知边长为 2的等边 ABC,点D、E分别是边 AC、AB上的点,满足DE // BC且
AD
( (0,1)),将 ADE沿直线DE折到 A DE的位置,在翻折过程中,下列
AC
结论成立的是 ( )
A. 直线 BC //平面A DE
B.在边 A E 上存在点 F ,使得在翻折过程中,满足直线 BF //平面A CD
1C.若 ,当二面角 A DE B等于 60° A B 7时,2 2
1 D.存在 0, ,使得在翻折过程中的某个位置,满足平面 A BC 平面 BCDE
2
三、填空题:本题共 4小题,每小题 5分,共 20分。
x2 y2
13. 双曲线 1的渐近线方程是 ;
9 4
14. 若三点 A(0,1),B(a,0),C(3,2)在同一条直线上,则a的值为 .
2 2
15. F x y已知 1,F2为椭圆 C: 1的两个焦点,P,Q 为 C 上关于坐标原点对称的两点,25 9
且 PQ F1F2 ,则四边形 PF1QF2的面积为 .
16.已知正方体的 ABCD A1B1C1D1 棱长为2,点M ,N分别是棱 BC,C1D1的中点,点 P
在平面 A1B1C1D1内,点Q在线段 A1N 上,若PM 6,则 PQ长度的最小值为 .
(高二数学试卷 第 2 页,共 4 页)
{#{QQABDYyUogCgQAJAAQhCEwGgCACQkACCCAoGhAAMIAIBQRFABAA=}#}
四、解答题:本题共 6小题,共 70分。解答应写出文字说明、证明过程或演算步骤。
17.(5+5=10分)如图所示,平行六面体 ABCD-A1B1C1D1 中,以顶点 A为端点的三条棱
长都为 2,且两两夹角为 60 ,AC 与 BD 的交点为 O,点 M 在 BC 上,且
BM=2MC , AB a,AD b,AA c .
(1)用 a,b,c表示 AC , OM ;
(2)求 AC 的长度.
18.(6+6=12 分)在平面直角坐标系 xOy 中,圆 C 的半径 r 2,圆心是直线
l1 : 2x y 4 0与 l2 : x y 1 0的交点 C.
(1)求圆 C的方程;
(2)判断直线 l3 : 4x 3y 1 0与圆 C的位置关系,如果相交,设交点为 A,B,
并求弦长 AB 的大小。
2 2
19.(6+6=12 x y 1分)已知椭圆 C: a2
2 1(a b 0)b 的长轴长等于 6,离心率
e
3 .
(1)求椭圆 C 的方程;
(2)椭圆 C 的左、右焦点分别为 F1,F2,点 P 在椭圆上,且 PF1F2 60 ,求 PF1F2的
面积。
(高二数学试卷 第 3 页,共 4 页)
{#{QQABDYyUogCgQAJAAQhCEwGgCACQkACCCAoGhAAMIAIBQRFABAA=}#}
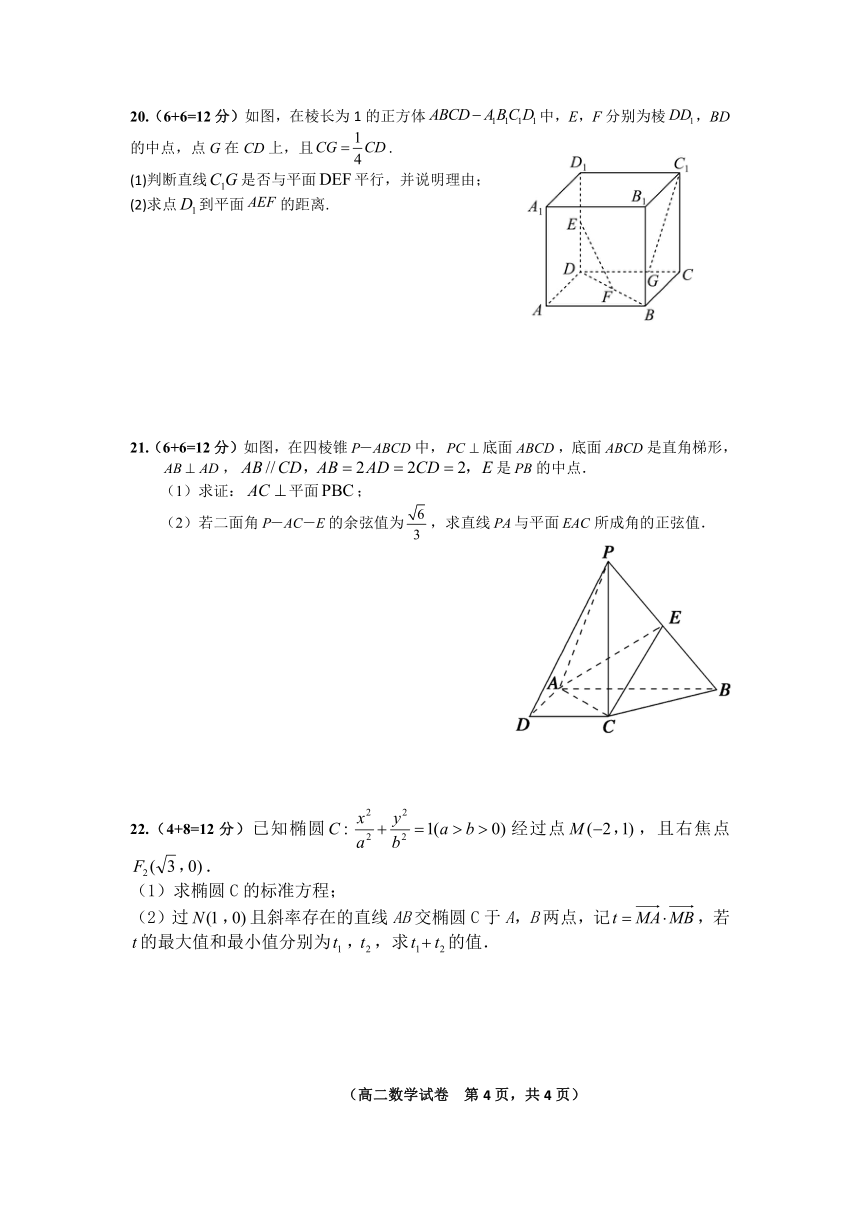
20.(6+6=12分)如图,在棱长为 1 的正方体 ABCD A1B1C1D1中,E,F分别为棱DD1,BD
1
的中点,点 G在 CD上,且CG CD .
4
(1)判断直线C1G是否与平面DEF平行,并说明理由;
(2)求点D 到平面 AEF1 的距离.
21.(6+6=12分)如图,在四棱锥 P-ABCD中,PC 底面 ABCD,底面 ABCD是直角梯形,
AB AD, AB //CD,AB 2AD 2CD 2,E是 PB的中点.
(1)求证: AC 平面PBC;
2 P AC E 6( )若二面角 - - 的余弦值为 ,求直线 PA与平面 EAC 所成角的正弦值.
3
x2 y2
22.(4+8=12 分)已知椭圆C : 2 2 1(a b 0) 经过点M ( 2,1),且右焦点a b
F2 ( 3,0).
(1)求椭圆 C的标准方程;
(2)过N (1,0)且斜率存在的直线 AB 交椭圆 C于 A,B两点,记 t MA MB,若
t的最大值和最小值分别为 t1 ,t2,求 t1 t2的值.
(高二数学试卷 第 4 页,共 4 页)
{#{QQABDYyUogCgQAJAAQhCEwGgCACQkACCCAoGhAAMIAIBQRFABAA=}#}
厦门市杏南中学 2023-2024 学年学年上学期期中阶段测试卷
高二年 数学
作答时间:120 分钟
1. 直线 3x y 1 0的倾斜角是 ( B )
A. 30 B. 60 C. 120 D. 150
2. 直线 l1 :ax 2y 3 0 与直线 l2 : x (a 1)y 2 0互相垂直,则 a ( C )
A. 0 B. 1 C. 2 D. 1
x2 y2
3. 已知椭圆 C: 19 7 的左、右焦点分别为 F1,F2,且
PF1 2,则 PF2 ( A )
A. 4 B. 6 C. 2 7 2 D. 2 2 2
4. 已知直线 l : x 2y 1 0 2 2经过圆C : x y Dx 2y 3 0的圆心,则D ( A )
A. 6 B. 2 C. 2 D. 6
5. 如图,在正方体 ABCD A1B1C1D1中,M是 AB的中点,则异面直线DB1,CM 所成
角的余弦值是 ( D )
2 15
A. B.
6 5
2 15
C. D.
15 15
6. 2已知圆C1 : x y
2 4x 2y 4 0 2与圆C2(: x 1) (y 3)
2 4,圆C1与圆C2的位
置关系是 ( B )
A. 外离 B. 外切 C. 相交 D. 内切
7. 在圆 x2 y2 9的上任取一点 P,过 P作 x轴的垂线段 PD,垂足为D,并延长DP至M ,
1
使得 PM DP ,则点M 的轨迹方程是 ( C )
3
x2 y2 1 x
2 y2 x2 y2 x2 y2
A. B. 1 C. 1 D. 1
9 4 16 9 9 16 3 4
x2 y2
8.已知椭圆 C: 2 2 1(a b 0)的右焦点为 F2,Oa b 为坐标原点为,
M 为 y 轴上一点,
点A是直线MF2与椭圆 C的一个交点,且 OA OF2 2OM ,则椭圆 C的离心率是( D )
1 2 5 5
A. B. C. D.
3 5 5 3
9. 已知直线 l : 4x 3y 2 0,下列说法正确的是 ( ABD )
1
A. 直线 l经过点 P(1,2) B. 直线 l与坐标轴围成的三角形面积是
6
C. l 8x 6y 7 0 1 D. l (x 1)2 (y 3)2直线 与直线 的距离是 直线 与圆 9相切
10. 2已知双曲线C : x y2 4,下列说法正确的是 ( BD )
x2
A. 双曲线C的实轴长是 2 B. 2双曲线C与椭圆 y 1有相同的焦点
9
C. 双曲线C的离心率 e 2 D. 直线 y 2x与双曲线C没有公共点
{#{QQABDYyUogCgQAJAAQhCEwGgCACQkACCCAoGhAAMIAIBQRFABAA=}#}
x2 y2
11. 已知椭圆 C: 19 4 的左、右焦点分别为 F1,F2,点 M 与焦点不重合。若 M 关于
F1,F2对称的点分别为 A,B,线段 MN 的中点 P 在椭圆 C 上,则 ( ACD )
A. 焦点分别为 F1,F2的坐标分别为( 5,0)(, 5,0)
B. 点 N 一定在椭圆 C 外
2 2
C. 当点 M x y与原点 O 重合时,点 N 的轨迹方程是 1
36 16
D. NA NB 12
12.已知边长为 2的等边 ABC,点D、E分别是边 AC、AB上的点,满足DE // BC且
AD
( (0,1)),将 ADE沿直线DE折到 A DE的位置,在翻折过程中,下列
AC
结论成立的是 ( AC )
A. 直线 BC //平面A DE
B.在边 A E 上存在点 F ,使得在翻折过程中,满足直线 BF //平面A CD
1
C A DE B 7.若 ,当二面角 等于 60°时,
2 A B 2
1
D.存在 0, ,使得在翻折过程中的某个位置,满足平面 A BC 平面 BCDE
2
x2 y2 2
13. 双曲线 1的渐近线方程是 y x ;
9 4 3
14. 若三点 A(0,1),B(a,0),C(3,2)在同一条直线上,则a的值为 3 .
2 2
15. 已知 F x y1,F2为椭圆 C: 1的两个焦点,P,Q 为 C 上关于坐标原点对称的两点,25 9
且 PQ F1F2 ,则四边形 PF1QF2的面积为 18 .
16.已知正方体的 ABCD A1B1C1D1 棱长为2,点M ,N 分别是棱 BC,C1D1 的中点,点 P
在平面 A1B1C1D1内,点Q在线段 A1N 上,若 PM 6,则 PQ长度的最小值为 0 .
17.如图所示,平行六面体 ABCD-A1B1C1D1 中,以顶点 A为端点的三条棱长都为 2,且
两两夹角为 60 ,AC与 BD的交点为 O,点 M在 BC 上,且 BM=2MC ,
{#{QQABDYyUogCgQAJAAQhCEwGgCACQkACCCAoGhAAMIAIBQRFABAA=}#}
AB a,AD b,AA c .
(1)用 a,b,c表示 AC , OM ;
(2)求 AC 的长度.
解:(1) AC AB BC CC
AB AD AA a b c ------------3 分
OM OB BM 1 2 DB BC
2 3
1
(AB AD) 2 (AD AA )
2 3
1 -----------6 分
AB 1 AD 2 1 AA a 1 2 b c
2 6 3 2 6 3
(2) 由(1)知 AC a b c ----------------------------------------------------7 分
2 2 2 2
AC (a b c)2 a b c 2a b 2b c 2a c ---------------8 分
2 2 2
a b c 2 a b cos60 2b c cos60 2 a c cos60 -----10分
4 4 4 2 2 2 1 1 1 2 2 2 2 2 2 =24
2 2 2 -----11分
AC 2 6. 即 AC 的长度为 2 6 。--------------------------------12分
18. 在平面直角坐标系 xOy 中,圆 C的半径 r 2,圆心是直线 l1 : 2x y 4 0与
l2 : x y 1 0的交点.
(1)求圆 C的方程;
(2)判断直线 l3 : 4x 3y 1 0与圆 C的位置关系,如果相交,设交点为 A,B,
并求弦长 AB 的大小。
2x y 4 0 x 3
解:(1)由 x y 1 0 得 y 2 ,
C(3,2)
---------------------------4 分
因为圆 C的半径 r 2,
2 2
所以圆 C的方程为(x 3) (y 2) 4. ---------------------------6 分
(2)由(1)知圆 C的方程为(x 3)2 (y 2)2 4,
圆心 C(3,2)到直线 l3 : 4x 3y 1 0的距离为
12 6 1
d 1 r
5 ---------------------------8 分
直线与圆相交. ---------------------------9 分
2 2弦长 AB 2 r d 2 4 1 2 3,
即弦长 AB 的大小为 2 3. ---------------------------12分
{#{QQABDYyUogCgQAJAAQhCEwGgCACQkACCCAoGhAAMIAIBQRFABAA=}#}
x2 y2 1
19.已知椭圆 C: 2 2 1(a b 0)的长轴长等于 6,离心率 e a b 3 .
(1)求椭圆 C 的方程;
(2)椭圆 C 的左、右焦点分别为 F1,F2,点 P 在椭圆上,且 PF1F2 60 ,求 PF1F2的
面积。
解:(1)依题意, 2a 6, a 3. ---------------------------2 分
e 1 c 1 ,即 , c 1.
3 a 3 ---------------------------3 分
b a2 c2 2 2. --------------------------4 分
x2 y2
椭圆 C 的方程为 1.9 8 ---------------------------6 分
(2)由(1)知, a 3, c 1,
设 PF1 m , PF2 n, 则
m n 6
2
m (2c)
2 2m 2c cos60 n2
m n 6 (i)
即 m2 4c2 2mc n2 (ii) ---------------------------8 分
在把 n 6 m,c 1代入 (ii) , 得
m2 4 2m 36 12m m2 ,
10m 32, m 16 即 ,
5
n 6 14 m .
5 ---------------------------10分
1
S PF m 2c sin 60
1F2 2
1 16 3
2
2 5 2
8 3
.
5
PF1F
8 3
2的面积为 .5 ---------------------------12分
20. 如图,在棱长为 1 的正方体 ABCD A1B1C1D1中,E,F分别为棱DD1,BD的中点,点
{#{QQABDYyUogCgQAJAAQhCEwGgCACQkACCCAoGhAAMIAIBQRFABAA=}#}
1
G在 CD上,且CG CD .
4
(1)判断直线C1G是否与平面DEF平行,并说明理由;
(2)求点D1到平面 AEF 的距离.
解: (1)答:直线C G与平面DEF不平行。------------1 分1
下面给予证明:
以 D 为原点,如图建立空间直角坐标系Dxyz,则
D(0,0,0),E(0,0, 1 1 1),F ( , ,0) ,
2 2 2
C(0,1,0),C 31(0,1,1),G(0, ,0) , A(1,0,0)4 ----------------------------2 分
DE (0,0, 1) , DF (1 , 1 ,0), C G (0, 1 , 1) , AC ( 1,1,0)
2 2 2 1 4
AC DE 0 , AC DF 0 ,
AC是平面DEF的法向量. ----------------------------4 分
AC C 1 11G 0 0 0,4 4
直线C1G与平面DEF不平行. ----------------------------6 分
(2)由(1)知, AE ( 1,0, 1 ) , AF ( 1 , 1 ,0),
2 2 2 ----------------------------7 分
设 n (x, y, z)是平面 AEF 的法向量,则
1
n AE 0 x z 0
, 2 ,
n AF 0 1 1 x y 0
2 2
取 x 1,则 z 2, y 1. n (1,1,2). ----------------------------9 分
D1(0,0,1), A(1,0,0), D1A (1,0, 1), ----------------------------10分
DA1 n 1 0 2 6
点D1到平面 AEF 的距离是 d .
n 6 6
6
即点D 到平面 AEF1 的距离为 .6 ----------------------------12分
{#{QQABDYyUogCgQAJAAQhCEwGgCACQkACCCAoGhAAMIAIBQRFABAA=}#}
21.如图,在四棱锥 P-ABCD中, PC 底面 ABCD,底面 ABCD是直角梯形, AB AD,
AB //CD,AB 2AD 2CD 2,E是 PB的中点.
(1)求证: AC 平面PBC;
(2)若二面角 P-AC 6-E的余弦值为 ,求直线 PA与平面 EAC 所成角的正弦值.
3
12.(1)证明:因为 PC 平面 ABCD,
AC 平面 ABCD,
所以 AC PC. ----------------------------2 分
因为 AB=2,AD=CD=1,
所以 AC=BC= 2.
所以 AC 2+BC 2=AB2 .
所以 AC BC. -----------------------------------------------4 分
又 BC PC=C, BC,PC 平面PBC,
所以 AC 平面 PBC . -------------------------------------------------------6 分
(2)解:如图,以点C为原点,DA,CD,CP分别为 x轴、 y轴、 z轴正方向建立空间
直角坐标系, -------------------7 分
则C(0,0,0), A(1,1,0) , B(1,-1,0),设 P(0,0,a)(a 0),
E 1 , 1 a
则 ,
,CA=(1,1,0),CP =(0,0,a)
1 1 a
,CE= , , .2 2 2 2 2 2 -------------------8 分
取 m =(1,-1,0),因为 m CA m CP 0,所以 m 为平面 PAC 的法向量.
n (x y z) EAC n CA n CE 0
x y 0
设 = , , 为平面 的法向量,则 ,即
x y az 0
取 x=a,y=-a,z=-2,则 n = (a,-a,-2), -------------------9 分
依题意, | cos m,n | n m a 6 = = = ,则 a=2.
n m a2+2 3 -------------------10分
于是 n =(2,-2,-2), PA=(1,1,-2).
设直线 PA与平面 EAC 所成角为 ,则 sin = | cos PA, n | P A n 2 = = ,
PA n 3
即直线 PA与平面 EAC 2所成角的正弦值为
3 ------------------12分.
{#{QQABDYyUogCgQAJAAQhCEwGgCACQkACCCAoGhAAMIAIBQRFABAA=}#}
x2 y2
22. 已知椭圆C : 2 2 1(a b 0)经过点M ( 2,1),且右焦点 F2 ( 3,0).a b
(1)求椭圆 C的标准方程;
(2)过N (1,0)且斜率存在的直线 AB 交椭圆 C于 A,B两点,记 t MA MB,若
t的最大值和最小值分别为 t1 ,t2,求 t1 t2的值.
解:(1)由椭圆 C的右焦点为 F ( 3,0),知 a2 b2 3,即b2 a2 3,
x2 y2
则 2 2 1, a
2 3.
a a 3 -------------------1 分
4 1
又椭圆 C过点M ( 2,1),所以 1,又 a22 2 3,所以 a
2 6.
a a 3 -------3 分
x2 y2
所以椭圆 C的标准方程为 1.
6 3 ------------------------------4 分
(2)设直线 AB 的方程为 y k (x 1), A x1, y1 , B x2 , y2 ,------------5 分
x2 y2
1,
由 2 2 2 6 3 得 x 2k (x 1) 6,即 (1 2k 2 )x2 4k 2x 2k 2 6 0 ,
y k (x 1),
-----------------------------6 分
因为点 N (1,0)在椭圆 C内部,所以 0,
x x 4k
2 2
所以 1 2 2 , x1x
2k 6
,
1 2k 2 1 2k 2 -----------------------------7 分
所以 t MA MB x1 2 x2 2 y1 1 y2 1 -----------------8 分
(1 k 2 )x x 21 2 (2 k k)(x1 x
2
2) k 2k 5
2
(1 k 2 ) 2k 6
2
2 (2
4k
k 2 k) 2 k
2 2k 5
1 2k 1 2k
15k 2 2k 1
,
1 2k 2 -------------------------------9 分
所以 (15 2t)k 2 2k 1 t 0,k R,则 1 4 4(15 2t)(1 t) 0 ,
所以 2t 2 13t 16 0, -------------------------------11分
由题意知 t1, t2是方程 2t
2 13t 16 0的两根,
∴ t1 t
13
2 .2 -------------------------------12分
{#{QQABDYyUogCgQAJAAQhCEwGgCACQkACCCAoGhAAMIAIBQRFABAA=}#}
高二年 数学
作答时间:120 分钟
一、单选题:本题共 8小题,每小题 5分,共 40分。在每小题给出的四个选项中,只有一
项是符合题目要求的。
1. 直线 3x y 1 0的倾斜角是 ( )
A. 30 B. 60 C. 120 D. 150
2. 直线 l1 :ax 2y 3 0 与直线 l2 : x (a 1)y 2 0互相垂直,则 a ( )
A. 0 B. 1 C. 2 D. 1
x2 y2
3. 已知椭圆 C: 1的左、右焦点分别为 F1,F2,且 PF1 2,则 PF2 ( )9 7
A. 4 B. 6 C. 2 7 2 D. 2 2 2
4. 已知直线 l : x 2y 1 0 C : x2 y2经过圆 Dx 2y 3 0的圆心,则D ( )
A. 6 B. 2 C. 2 D. 6
5. 如图,在正方体 ABCD A1B1C1D1中,M是 AB的中点,则异面直线DB1,CM 所成
角的余弦值是 ( )
2 15
A. B.
6 5
2 15
C. D.
15 15
6. 2 2已知圆C1 : x y 4x 2y 4 0 C (: x 1)
2
与圆 2 (y 3)
2 4,圆C1与圆C2的位
置关系是 ( )
A. 外离 B. 外切 C. 相交 D. 内切
7. x2 y2在圆 9的上任取一点 P,过 P作 x轴的垂线段 PD,垂足为D,并延长DP至M ,
PM 1使得 DP ,则点M 的轨迹方程是 ( )
3
x2 y2 x2 y2 x2 y2 x2 y2
A. 1 B. 1 C. 1 D. 1
9 4 16 9 9 16 3 4
x2 y2
8.已知椭圆 C: 2 2 1(a b 0)a b 的右焦点为
F2,O 为坐标原点为,M 为 y 轴上一点,
点 A是直线MF2与椭圆 C的一个交点,且 OA OF2 2OM ,则椭圆 C的离心率是( )
1 2 5 5
A. B. C. D.
3 5 5 3
二、选择题多选题:本题共 4小题,每小题 5分,共 20分。在每小题给出的四个选项中,
有多个选项符合题目要求,全部选对的得 5分,选对但不全的得 2分,有选错的得 0分。
9. 已知直线 l : 4x 3y 2 0,下列说法正确的是 ( )
1
A. 直线 l经过点 P(1,2) B. 直线 l与坐标轴围成的三角形面积是
6
C. 直线 l与直线8x 6y 7 0 2的距离是 1 D. 直线 l与圆(x 1) (y 3)2 9相切
(高二数学试卷 第 1 页,共 4 页)
{#{QQABDYyUogCgQAJAAQhCEwGgCACQkACCCAoGhAAMIAIBQRFABAA=}#}
10. 2已知双曲线C : x y2 4,下列说法正确的是 ( )
x2
A. 双曲线C的实轴长是 2 B. 2双曲线C与椭圆 y 1有相同的焦点
9
C. 双曲线C的离心率 e 2 D. 直线 y 2x与双曲线C没有公共点
x2 y2
11. 已知椭圆 C: 19 4 的左、右焦点分别为 F1,F2,点 M 与焦点不重合。若 M 关于
F1,F2对称的点分别为 A,B,线段 MN 的中点 P 在椭圆 C 上,则 ( )
A. 焦点分别为 F1,F2的坐标分别为( 5,0)(, 5,0)
B. 点 N 一定在椭圆 C 外
2
C. M O N x y
2
当点 与原点 重合时,点 的轨迹方程是 1
36 16
D. NA NB 12
12.已知边长为 2的等边 ABC,点D、E分别是边 AC、AB上的点,满足DE // BC且
AD
( (0,1)),将 ADE沿直线DE折到 A DE的位置,在翻折过程中,下列
AC
结论成立的是 ( )
A. 直线 BC //平面A DE
B.在边 A E 上存在点 F ,使得在翻折过程中,满足直线 BF //平面A CD
1C.若 ,当二面角 A DE B等于 60° A B 7时,2 2
1 D.存在 0, ,使得在翻折过程中的某个位置,满足平面 A BC 平面 BCDE
2
三、填空题:本题共 4小题,每小题 5分,共 20分。
x2 y2
13. 双曲线 1的渐近线方程是 ;
9 4
14. 若三点 A(0,1),B(a,0),C(3,2)在同一条直线上,则a的值为 .
2 2
15. F x y已知 1,F2为椭圆 C: 1的两个焦点,P,Q 为 C 上关于坐标原点对称的两点,25 9
且 PQ F1F2 ,则四边形 PF1QF2的面积为 .
16.已知正方体的 ABCD A1B1C1D1 棱长为2,点M ,N分别是棱 BC,C1D1的中点,点 P
在平面 A1B1C1D1内,点Q在线段 A1N 上,若PM 6,则 PQ长度的最小值为 .
(高二数学试卷 第 2 页,共 4 页)
{#{QQABDYyUogCgQAJAAQhCEwGgCACQkACCCAoGhAAMIAIBQRFABAA=}#}
四、解答题:本题共 6小题,共 70分。解答应写出文字说明、证明过程或演算步骤。
17.(5+5=10分)如图所示,平行六面体 ABCD-A1B1C1D1 中,以顶点 A为端点的三条棱
长都为 2,且两两夹角为 60 ,AC 与 BD 的交点为 O,点 M 在 BC 上,且
BM=2MC , AB a,AD b,AA c .
(1)用 a,b,c表示 AC , OM ;
(2)求 AC 的长度.
18.(6+6=12 分)在平面直角坐标系 xOy 中,圆 C 的半径 r 2,圆心是直线
l1 : 2x y 4 0与 l2 : x y 1 0的交点 C.
(1)求圆 C的方程;
(2)判断直线 l3 : 4x 3y 1 0与圆 C的位置关系,如果相交,设交点为 A,B,
并求弦长 AB 的大小。
2 2
19.(6+6=12 x y 1分)已知椭圆 C: a2
2 1(a b 0)b 的长轴长等于 6,离心率
e
3 .
(1)求椭圆 C 的方程;
(2)椭圆 C 的左、右焦点分别为 F1,F2,点 P 在椭圆上,且 PF1F2 60 ,求 PF1F2的
面积。
(高二数学试卷 第 3 页,共 4 页)
{#{QQABDYyUogCgQAJAAQhCEwGgCACQkACCCAoGhAAMIAIBQRFABAA=}#}
20.(6+6=12分)如图,在棱长为 1 的正方体 ABCD A1B1C1D1中,E,F分别为棱DD1,BD
1
的中点,点 G在 CD上,且CG CD .
4
(1)判断直线C1G是否与平面DEF平行,并说明理由;
(2)求点D 到平面 AEF1 的距离.
21.(6+6=12分)如图,在四棱锥 P-ABCD中,PC 底面 ABCD,底面 ABCD是直角梯形,
AB AD, AB //CD,AB 2AD 2CD 2,E是 PB的中点.
(1)求证: AC 平面PBC;
2 P AC E 6( )若二面角 - - 的余弦值为 ,求直线 PA与平面 EAC 所成角的正弦值.
3
x2 y2
22.(4+8=12 分)已知椭圆C : 2 2 1(a b 0) 经过点M ( 2,1),且右焦点a b
F2 ( 3,0).
(1)求椭圆 C的标准方程;
(2)过N (1,0)且斜率存在的直线 AB 交椭圆 C于 A,B两点,记 t MA MB,若
t的最大值和最小值分别为 t1 ,t2,求 t1 t2的值.
(高二数学试卷 第 4 页,共 4 页)
{#{QQABDYyUogCgQAJAAQhCEwGgCACQkACCCAoGhAAMIAIBQRFABAA=}#}
厦门市杏南中学 2023-2024 学年学年上学期期中阶段测试卷
高二年 数学
作答时间:120 分钟
1. 直线 3x y 1 0的倾斜角是 ( B )
A. 30 B. 60 C. 120 D. 150
2. 直线 l1 :ax 2y 3 0 与直线 l2 : x (a 1)y 2 0互相垂直,则 a ( C )
A. 0 B. 1 C. 2 D. 1
x2 y2
3. 已知椭圆 C: 19 7 的左、右焦点分别为 F1,F2,且
PF1 2,则 PF2 ( A )
A. 4 B. 6 C. 2 7 2 D. 2 2 2
4. 已知直线 l : x 2y 1 0 2 2经过圆C : x y Dx 2y 3 0的圆心,则D ( A )
A. 6 B. 2 C. 2 D. 6
5. 如图,在正方体 ABCD A1B1C1D1中,M是 AB的中点,则异面直线DB1,CM 所成
角的余弦值是 ( D )
2 15
A. B.
6 5
2 15
C. D.
15 15
6. 2已知圆C1 : x y
2 4x 2y 4 0 2与圆C2(: x 1) (y 3)
2 4,圆C1与圆C2的位
置关系是 ( B )
A. 外离 B. 外切 C. 相交 D. 内切
7. 在圆 x2 y2 9的上任取一点 P,过 P作 x轴的垂线段 PD,垂足为D,并延长DP至M ,
1
使得 PM DP ,则点M 的轨迹方程是 ( C )
3
x2 y2 1 x
2 y2 x2 y2 x2 y2
A. B. 1 C. 1 D. 1
9 4 16 9 9 16 3 4
x2 y2
8.已知椭圆 C: 2 2 1(a b 0)的右焦点为 F2,Oa b 为坐标原点为,
M 为 y 轴上一点,
点A是直线MF2与椭圆 C的一个交点,且 OA OF2 2OM ,则椭圆 C的离心率是( D )
1 2 5 5
A. B. C. D.
3 5 5 3
9. 已知直线 l : 4x 3y 2 0,下列说法正确的是 ( ABD )
1
A. 直线 l经过点 P(1,2) B. 直线 l与坐标轴围成的三角形面积是
6
C. l 8x 6y 7 0 1 D. l (x 1)2 (y 3)2直线 与直线 的距离是 直线 与圆 9相切
10. 2已知双曲线C : x y2 4,下列说法正确的是 ( BD )
x2
A. 双曲线C的实轴长是 2 B. 2双曲线C与椭圆 y 1有相同的焦点
9
C. 双曲线C的离心率 e 2 D. 直线 y 2x与双曲线C没有公共点
{#{QQABDYyUogCgQAJAAQhCEwGgCACQkACCCAoGhAAMIAIBQRFABAA=}#}
x2 y2
11. 已知椭圆 C: 19 4 的左、右焦点分别为 F1,F2,点 M 与焦点不重合。若 M 关于
F1,F2对称的点分别为 A,B,线段 MN 的中点 P 在椭圆 C 上,则 ( ACD )
A. 焦点分别为 F1,F2的坐标分别为( 5,0)(, 5,0)
B. 点 N 一定在椭圆 C 外
2 2
C. 当点 M x y与原点 O 重合时,点 N 的轨迹方程是 1
36 16
D. NA NB 12
12.已知边长为 2的等边 ABC,点D、E分别是边 AC、AB上的点,满足DE // BC且
AD
( (0,1)),将 ADE沿直线DE折到 A DE的位置,在翻折过程中,下列
AC
结论成立的是 ( AC )
A. 直线 BC //平面A DE
B.在边 A E 上存在点 F ,使得在翻折过程中,满足直线 BF //平面A CD
1
C A DE B 7.若 ,当二面角 等于 60°时,
2 A B 2
1
D.存在 0, ,使得在翻折过程中的某个位置,满足平面 A BC 平面 BCDE
2
x2 y2 2
13. 双曲线 1的渐近线方程是 y x ;
9 4 3
14. 若三点 A(0,1),B(a,0),C(3,2)在同一条直线上,则a的值为 3 .
2 2
15. 已知 F x y1,F2为椭圆 C: 1的两个焦点,P,Q 为 C 上关于坐标原点对称的两点,25 9
且 PQ F1F2 ,则四边形 PF1QF2的面积为 18 .
16.已知正方体的 ABCD A1B1C1D1 棱长为2,点M ,N 分别是棱 BC,C1D1 的中点,点 P
在平面 A1B1C1D1内,点Q在线段 A1N 上,若 PM 6,则 PQ长度的最小值为 0 .
17.如图所示,平行六面体 ABCD-A1B1C1D1 中,以顶点 A为端点的三条棱长都为 2,且
两两夹角为 60 ,AC与 BD的交点为 O,点 M在 BC 上,且 BM=2MC ,
{#{QQABDYyUogCgQAJAAQhCEwGgCACQkACCCAoGhAAMIAIBQRFABAA=}#}
AB a,AD b,AA c .
(1)用 a,b,c表示 AC , OM ;
(2)求 AC 的长度.
解:(1) AC AB BC CC
AB AD AA a b c ------------3 分
OM OB BM 1 2 DB BC
2 3
1
(AB AD) 2 (AD AA )
2 3
1 -----------6 分
AB 1 AD 2 1 AA a 1 2 b c
2 6 3 2 6 3
(2) 由(1)知 AC a b c ----------------------------------------------------7 分
2 2 2 2
AC (a b c)2 a b c 2a b 2b c 2a c ---------------8 分
2 2 2
a b c 2 a b cos60 2b c cos60 2 a c cos60 -----10分
4 4 4 2 2 2 1 1 1 2 2 2 2 2 2 =24
2 2 2 -----11分
AC 2 6. 即 AC 的长度为 2 6 。--------------------------------12分
18. 在平面直角坐标系 xOy 中,圆 C的半径 r 2,圆心是直线 l1 : 2x y 4 0与
l2 : x y 1 0的交点.
(1)求圆 C的方程;
(2)判断直线 l3 : 4x 3y 1 0与圆 C的位置关系,如果相交,设交点为 A,B,
并求弦长 AB 的大小。
2x y 4 0 x 3
解:(1)由 x y 1 0 得 y 2 ,
C(3,2)
---------------------------4 分
因为圆 C的半径 r 2,
2 2
所以圆 C的方程为(x 3) (y 2) 4. ---------------------------6 分
(2)由(1)知圆 C的方程为(x 3)2 (y 2)2 4,
圆心 C(3,2)到直线 l3 : 4x 3y 1 0的距离为
12 6 1
d 1 r
5 ---------------------------8 分
直线与圆相交. ---------------------------9 分
2 2弦长 AB 2 r d 2 4 1 2 3,
即弦长 AB 的大小为 2 3. ---------------------------12分
{#{QQABDYyUogCgQAJAAQhCEwGgCACQkACCCAoGhAAMIAIBQRFABAA=}#}
x2 y2 1
19.已知椭圆 C: 2 2 1(a b 0)的长轴长等于 6,离心率 e a b 3 .
(1)求椭圆 C 的方程;
(2)椭圆 C 的左、右焦点分别为 F1,F2,点 P 在椭圆上,且 PF1F2 60 ,求 PF1F2的
面积。
解:(1)依题意, 2a 6, a 3. ---------------------------2 分
e 1 c 1 ,即 , c 1.
3 a 3 ---------------------------3 分
b a2 c2 2 2. --------------------------4 分
x2 y2
椭圆 C 的方程为 1.9 8 ---------------------------6 分
(2)由(1)知, a 3, c 1,
设 PF1 m , PF2 n, 则
m n 6
2
m (2c)
2 2m 2c cos60 n2
m n 6 (i)
即 m2 4c2 2mc n2 (ii) ---------------------------8 分
在把 n 6 m,c 1代入 (ii) , 得
m2 4 2m 36 12m m2 ,
10m 32, m 16 即 ,
5
n 6 14 m .
5 ---------------------------10分
1
S PF m 2c sin 60
1F2 2
1 16 3
2
2 5 2
8 3
.
5
PF1F
8 3
2的面积为 .5 ---------------------------12分
20. 如图,在棱长为 1 的正方体 ABCD A1B1C1D1中,E,F分别为棱DD1,BD的中点,点
{#{QQABDYyUogCgQAJAAQhCEwGgCACQkACCCAoGhAAMIAIBQRFABAA=}#}
1
G在 CD上,且CG CD .
4
(1)判断直线C1G是否与平面DEF平行,并说明理由;
(2)求点D1到平面 AEF 的距离.
解: (1)答:直线C G与平面DEF不平行。------------1 分1
下面给予证明:
以 D 为原点,如图建立空间直角坐标系Dxyz,则
D(0,0,0),E(0,0, 1 1 1),F ( , ,0) ,
2 2 2
C(0,1,0),C 31(0,1,1),G(0, ,0) , A(1,0,0)4 ----------------------------2 分
DE (0,0, 1) , DF (1 , 1 ,0), C G (0, 1 , 1) , AC ( 1,1,0)
2 2 2 1 4
AC DE 0 , AC DF 0 ,
AC是平面DEF的法向量. ----------------------------4 分
AC C 1 11G 0 0 0,4 4
直线C1G与平面DEF不平行. ----------------------------6 分
(2)由(1)知, AE ( 1,0, 1 ) , AF ( 1 , 1 ,0),
2 2 2 ----------------------------7 分
设 n (x, y, z)是平面 AEF 的法向量,则
1
n AE 0 x z 0
, 2 ,
n AF 0 1 1 x y 0
2 2
取 x 1,则 z 2, y 1. n (1,1,2). ----------------------------9 分
D1(0,0,1), A(1,0,0), D1A (1,0, 1), ----------------------------10分
DA1 n 1 0 2 6
点D1到平面 AEF 的距离是 d .
n 6 6
6
即点D 到平面 AEF1 的距离为 .6 ----------------------------12分
{#{QQABDYyUogCgQAJAAQhCEwGgCACQkACCCAoGhAAMIAIBQRFABAA=}#}
21.如图,在四棱锥 P-ABCD中, PC 底面 ABCD,底面 ABCD是直角梯形, AB AD,
AB //CD,AB 2AD 2CD 2,E是 PB的中点.
(1)求证: AC 平面PBC;
(2)若二面角 P-AC 6-E的余弦值为 ,求直线 PA与平面 EAC 所成角的正弦值.
3
12.(1)证明:因为 PC 平面 ABCD,
AC 平面 ABCD,
所以 AC PC. ----------------------------2 分
因为 AB=2,AD=CD=1,
所以 AC=BC= 2.
所以 AC 2+BC 2=AB2 .
所以 AC BC. -----------------------------------------------4 分
又 BC PC=C, BC,PC 平面PBC,
所以 AC 平面 PBC . -------------------------------------------------------6 分
(2)解:如图,以点C为原点,DA,CD,CP分别为 x轴、 y轴、 z轴正方向建立空间
直角坐标系, -------------------7 分
则C(0,0,0), A(1,1,0) , B(1,-1,0),设 P(0,0,a)(a 0),
E 1 , 1 a
则 ,
,CA=(1,1,0),CP =(0,0,a)
1 1 a
,CE= , , .2 2 2 2 2 2 -------------------8 分
取 m =(1,-1,0),因为 m CA m CP 0,所以 m 为平面 PAC 的法向量.
n (x y z) EAC n CA n CE 0
x y 0
设 = , , 为平面 的法向量,则 ,即
x y az 0
取 x=a,y=-a,z=-2,则 n = (a,-a,-2), -------------------9 分
依题意, | cos m,n | n m a 6 = = = ,则 a=2.
n m a2+2 3 -------------------10分
于是 n =(2,-2,-2), PA=(1,1,-2).
设直线 PA与平面 EAC 所成角为 ,则 sin = | cos PA, n | P A n 2 = = ,
PA n 3
即直线 PA与平面 EAC 2所成角的正弦值为
3 ------------------12分.
{#{QQABDYyUogCgQAJAAQhCEwGgCACQkACCCAoGhAAMIAIBQRFABAA=}#}
x2 y2
22. 已知椭圆C : 2 2 1(a b 0)经过点M ( 2,1),且右焦点 F2 ( 3,0).a b
(1)求椭圆 C的标准方程;
(2)过N (1,0)且斜率存在的直线 AB 交椭圆 C于 A,B两点,记 t MA MB,若
t的最大值和最小值分别为 t1 ,t2,求 t1 t2的值.
解:(1)由椭圆 C的右焦点为 F ( 3,0),知 a2 b2 3,即b2 a2 3,
x2 y2
则 2 2 1, a
2 3.
a a 3 -------------------1 分
4 1
又椭圆 C过点M ( 2,1),所以 1,又 a22 2 3,所以 a
2 6.
a a 3 -------3 分
x2 y2
所以椭圆 C的标准方程为 1.
6 3 ------------------------------4 分
(2)设直线 AB 的方程为 y k (x 1), A x1, y1 , B x2 , y2 ,------------5 分
x2 y2
1,
由 2 2 2 6 3 得 x 2k (x 1) 6,即 (1 2k 2 )x2 4k 2x 2k 2 6 0 ,
y k (x 1),
-----------------------------6 分
因为点 N (1,0)在椭圆 C内部,所以 0,
x x 4k
2 2
所以 1 2 2 , x1x
2k 6
,
1 2k 2 1 2k 2 -----------------------------7 分
所以 t MA MB x1 2 x2 2 y1 1 y2 1 -----------------8 分
(1 k 2 )x x 21 2 (2 k k)(x1 x
2
2) k 2k 5
2
(1 k 2 ) 2k 6
2
2 (2
4k
k 2 k) 2 k
2 2k 5
1 2k 1 2k
15k 2 2k 1
,
1 2k 2 -------------------------------9 分
所以 (15 2t)k 2 2k 1 t 0,k R,则 1 4 4(15 2t)(1 t) 0 ,
所以 2t 2 13t 16 0, -------------------------------11分
由题意知 t1, t2是方程 2t
2 13t 16 0的两根,
∴ t1 t
13
2 .2 -------------------------------12分
{#{QQABDYyUogCgQAJAAQhCEwGgCACQkACCCAoGhAAMIAIBQRFABAA=}#}
同课章节目录
