北师大九年级数学下3.2圆的对称性同步练习(含答案)
文档属性
| 名称 | 北师大九年级数学下3.2圆的对称性同步练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 148.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-24 13:56:39 | ||
图片预览


文档简介
3.2圆的对称性
一、选择题
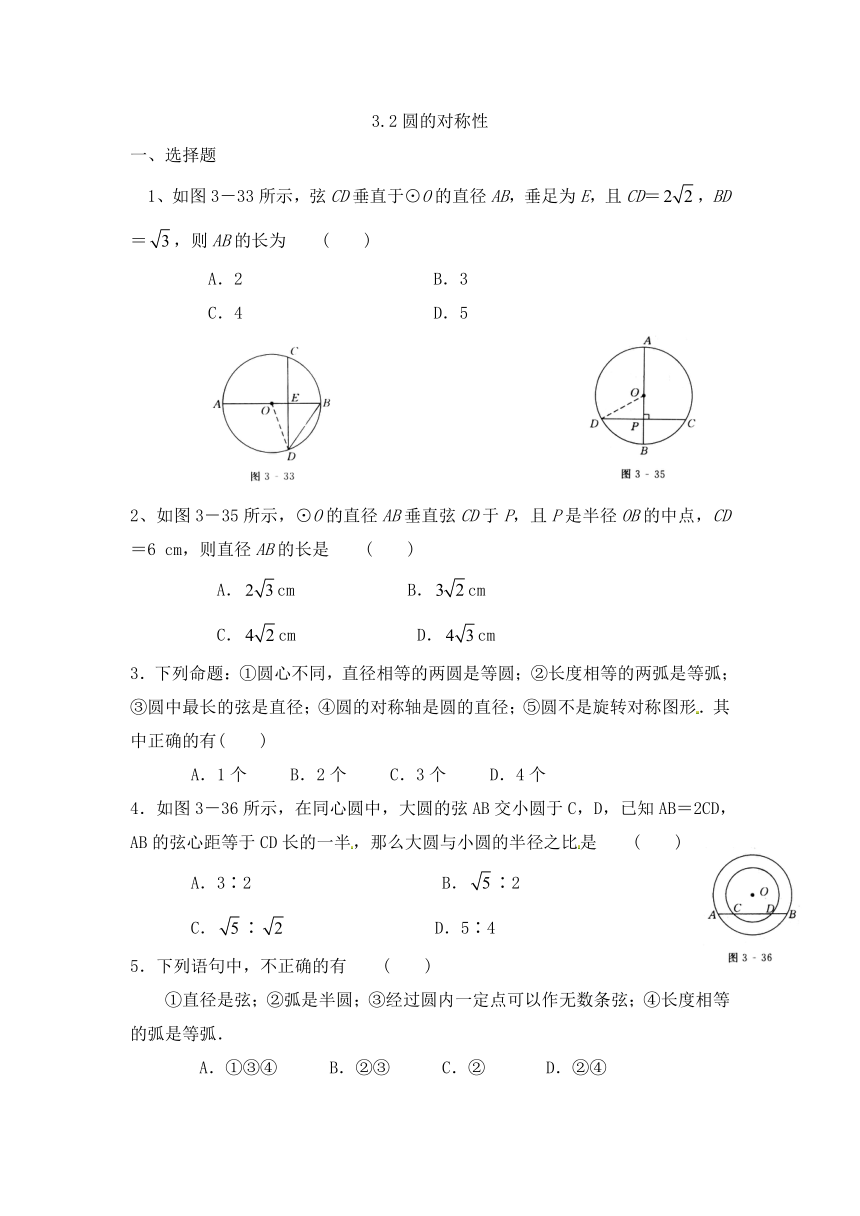
1、如图3-33所示,弦CD垂直于⊙O的直径AB,垂足为E,且CD=,BD=,则AB的长为 ( )
A.2 B.3
C.4 D.5
2、如图3-35所示,⊙O的直径AB垂直弦CD于P,且P是半径OB的中点,CD=6 cm,则直径AB的长是 ( )
A.cm B.cm
C.cm D.cm
3.下列命题:①圆心不同,直径相等的两圆是等圆;②长度相等的两弧是等弧;③圆中最长的弦是直径;④圆的对称轴是圆的直径;⑤圆不是旋转对称图形.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
4.如图3-36所示,在同心圆中,大圆的弦AB交小圆于C,D,已知AB=2CD,AB的弦心距等于CD长的一半,那么大圆与小圆的半径之比是 ( )
A.3∶2 B.∶2
C.∶ D.5∶4
5.下列语句中,不正确的有 ( )
①直径是弦;②弧是半圆;③经过圆内一定点可以作无数条弦;④长度相等的弧是等弧.
A.①③④ B.②③ C.② D.②④
6.下列语句中不正确的有
① 平分 弦的直径垂直于弦 ②圆是轴对称图形,任何一条直径都是它的对称轴 ③长度相等的两条弧是等弧
A.3个 B.2个
C.1个 D.以上都不对
7.如图3-37所示,在⊙O中,弦AB的长为6 cm.圆心O到AB的距离为4 cm,则⊙O的半径长为 ( )
A.3 cm B.4 cm C.5 cm D.6 cm
8.如图3-38所示,C为的中点,CN⊥OB于N,弦CD⊥OA于M.若⊙O的半径为5 cm,ON=4 cm,则CD的长等于 .
二、填空题
9.如图3-39所示,在⊙O中,AB和AC是互相垂直的两条弦,OD⊥AB于D,OE⊥AC于E.且AB=8 cm,AC=6 cm,那么⊙O的半径OA的长为 .
10.P为⊙O内一点,且OP=8 cm,过P的最长弦长为20 cm,则过P的最矩弦长为 .
11.如图,⊙O的半径为5,弦AB的长为8,M是弦AB上的动点,则线段OM的长的最小值为____.最大值为____________.
12.(2014 陕西,第17题3分)如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是 .
三、解答题
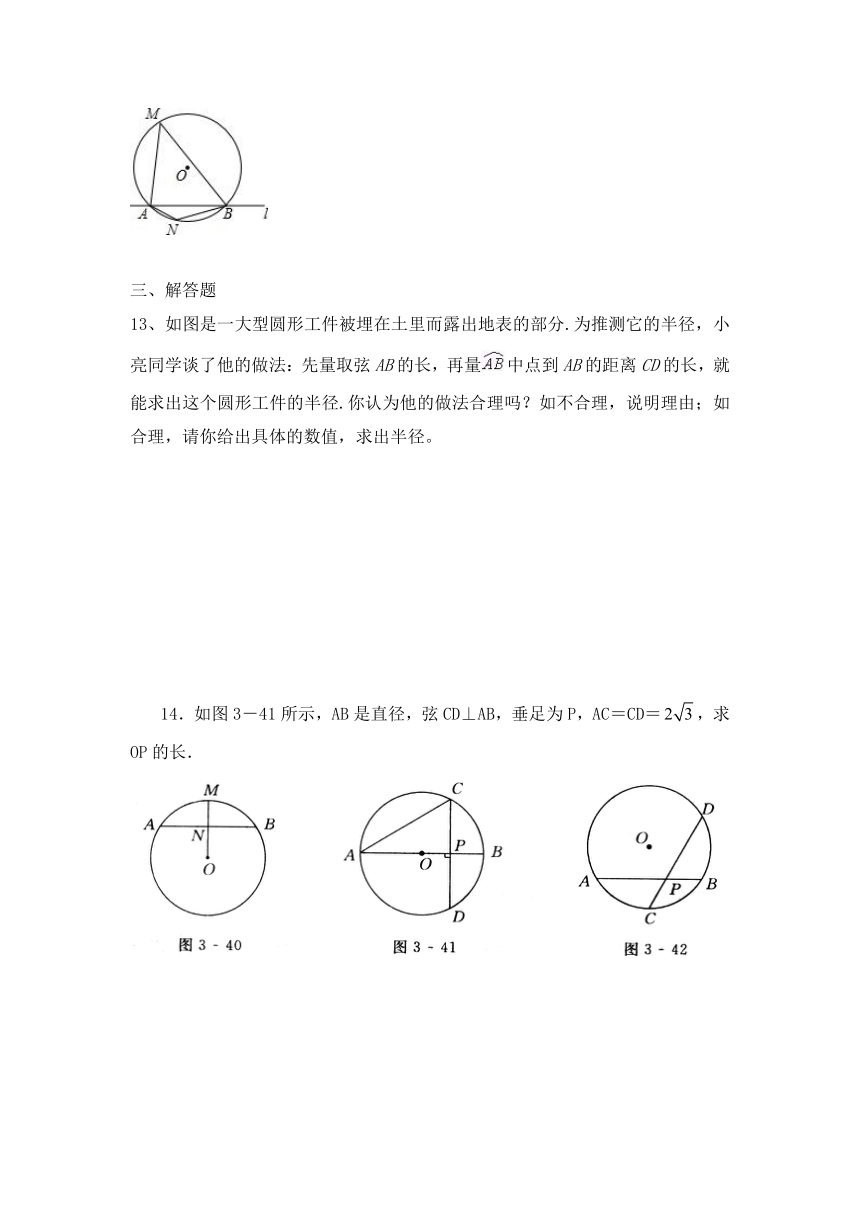
13、如图是一大型圆形工件被埋在土里而露出地表的部分.为推测它的半径,小亮同学谈了他的做法:先量取弦AB的长,再量中点到AB的距离CD的长,就能求出这个圆形工件的半径.你认为他的做法合理吗?如不合理,说明理由;如合理,请你给出具体的数值,求出半径。
14.如图3-41所示,AB是直径,弦CD⊥AB,垂足为P,AC=CD=,求OP的长.
15.如图3-42所示,⊙O的直径是4 cm,C是的中点,弦AB,CD相交于P,CD=cm,求∠APC的度数.
16.(2014 湖北黄石,第19题7分)如图,A、B是圆O上的两点,∠AOB=120°,C是AB弧的中点.
(1)求证:AB平分∠OAC;
(2)延长OA至P使得OA=AP,连接PC,若圆O的半径R=1,求PC的长.
参考答案
1.B
2.D
3..B[提示:①③正确.]
4.C[提示:AB与CD的弦心距相同.]
5.C
6.B
7.C[提示:本题考查垂径定理与勾股定理的综合应用.作OC⊥AB于点C,连接AO,则OC=4,AC=3,所以在Rt△AOC中,AO==5(cm).故选C.]
8.6 cm[提示:由题意可知CD=CE=2CN,又CN==3,所以CD=2CN=6(cm),故填6 cm.]
9.5 cm
10.12 cm[提示:过P的最长弦为直径,即直径等于20 cm,最短弦为过P且垂直OP的弦,利用勾股定理可求最短弦的一半长为6 cm,则弦长为12 cm.]
11、分析:当OM垂直于AB时OM最小,当M于A或B重合时,OM最大
解:当OM垂直于AB时OM最小,这时AM=1/2AB=4,连AO得直角三角形AOM,由勾股定理得,0M=3,当M于A或B重合时,OM最大为半径5
12.4 ( http: / / www." \o "中国教育出版网\ )
13、分析:由CD平分弧AB且垂直于AB,得CD经过圆心O,连AO,由垂径定理得AD=1/2AB, 设圆形工件半径为r,OD=OC-CD=r-CD,在直角三角形AOD中,由勾股定理,求出r。
解、小亮的做法合理.
取AB=8 m,CD=2 m, 设圆形工件半径为r,
∴r2=(r-2)2+42. 得r=5(m).
14.解:连接OC,∵AB是直径,CD⊥AB,∴CP=CD=.在Rt△ACP中,AP==3,∴OP=AP-AO=3-AO=3-OC.在Rt△COP中,OC2=OP2+CP2,即OC2=(3-OC)2+.解得OC=2.∴OP=3-2=1.
15.解:连接OC,交AB于E.∵C是的中点,∴OC⊥AB,∴∠PEC=90°.作OF⊥CD,垂足为F,∴CF=CD=(cm).∵⊙O的直径是4 cm,∴OC=2 cm.在Rt△COF中,cosC=,∴∠C=30°,∴∠APC=90°-30°=60°.
16.解答: (1)证明:连接OC,
∵∠AOB=120°,C是AB弧的中点,
∴∠AOC=∠BOC=60°,
∵OA=OC,
∴△ACO是等边三角形,
∴OA=AC,同理OB=BC,
∴OA=AC=BC=OB,
∴四边形AOBC是菱形,
∴AB平分∠OAC;
(2)解:连接OC,
∵C为弧AB中点,∠AOB=120°,
∴∠AOC=60°,
∵OA=OC,
∴OAC是等边三角形,
∵OA=AC,
∴AP=AC,
∴∠APC=30°,
∴△OPC是直角三角形,
∴.
一、选择题
1、如图3-33所示,弦CD垂直于⊙O的直径AB,垂足为E,且CD=,BD=,则AB的长为 ( )
A.2 B.3
C.4 D.5
2、如图3-35所示,⊙O的直径AB垂直弦CD于P,且P是半径OB的中点,CD=6 cm,则直径AB的长是 ( )
A.cm B.cm
C.cm D.cm
3.下列命题:①圆心不同,直径相等的两圆是等圆;②长度相等的两弧是等弧;③圆中最长的弦是直径;④圆的对称轴是圆的直径;⑤圆不是旋转对称图形.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
4.如图3-36所示,在同心圆中,大圆的弦AB交小圆于C,D,已知AB=2CD,AB的弦心距等于CD长的一半,那么大圆与小圆的半径之比是 ( )
A.3∶2 B.∶2
C.∶ D.5∶4
5.下列语句中,不正确的有 ( )
①直径是弦;②弧是半圆;③经过圆内一定点可以作无数条弦;④长度相等的弧是等弧.
A.①③④ B.②③ C.② D.②④
6.下列语句中不正确的有
① 平分 弦的直径垂直于弦 ②圆是轴对称图形,任何一条直径都是它的对称轴 ③长度相等的两条弧是等弧
A.3个 B.2个
C.1个 D.以上都不对
7.如图3-37所示,在⊙O中,弦AB的长为6 cm.圆心O到AB的距离为4 cm,则⊙O的半径长为 ( )
A.3 cm B.4 cm C.5 cm D.6 cm
8.如图3-38所示,C为的中点,CN⊥OB于N,弦CD⊥OA于M.若⊙O的半径为5 cm,ON=4 cm,则CD的长等于 .
二、填空题
9.如图3-39所示,在⊙O中,AB和AC是互相垂直的两条弦,OD⊥AB于D,OE⊥AC于E.且AB=8 cm,AC=6 cm,那么⊙O的半径OA的长为 .
10.P为⊙O内一点,且OP=8 cm,过P的最长弦长为20 cm,则过P的最矩弦长为 .
11.如图,⊙O的半径为5,弦AB的长为8,M是弦AB上的动点,则线段OM的长的最小值为____.最大值为____________.
12.(2014 陕西,第17题3分)如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是 .
三、解答题
13、如图是一大型圆形工件被埋在土里而露出地表的部分.为推测它的半径,小亮同学谈了他的做法:先量取弦AB的长,再量中点到AB的距离CD的长,就能求出这个圆形工件的半径.你认为他的做法合理吗?如不合理,说明理由;如合理,请你给出具体的数值,求出半径。
14.如图3-41所示,AB是直径,弦CD⊥AB,垂足为P,AC=CD=,求OP的长.
15.如图3-42所示,⊙O的直径是4 cm,C是的中点,弦AB,CD相交于P,CD=cm,求∠APC的度数.
16.(2014 湖北黄石,第19题7分)如图,A、B是圆O上的两点,∠AOB=120°,C是AB弧的中点.
(1)求证:AB平分∠OAC;
(2)延长OA至P使得OA=AP,连接PC,若圆O的半径R=1,求PC的长.
参考答案
1.B
2.D
3..B[提示:①③正确.]
4.C[提示:AB与CD的弦心距相同.]
5.C
6.B
7.C[提示:本题考查垂径定理与勾股定理的综合应用.作OC⊥AB于点C,连接AO,则OC=4,AC=3,所以在Rt△AOC中,AO==5(cm).故选C.]
8.6 cm[提示:由题意可知CD=CE=2CN,又CN==3,所以CD=2CN=6(cm),故填6 cm.]
9.5 cm
10.12 cm[提示:过P的最长弦为直径,即直径等于20 cm,最短弦为过P且垂直OP的弦,利用勾股定理可求最短弦的一半长为6 cm,则弦长为12 cm.]
11、分析:当OM垂直于AB时OM最小,当M于A或B重合时,OM最大
解:当OM垂直于AB时OM最小,这时AM=1/2AB=4,连AO得直角三角形AOM,由勾股定理得,0M=3,当M于A或B重合时,OM最大为半径5
12.4 ( http: / / www." \o "中国教育出版网\ )
13、分析:由CD平分弧AB且垂直于AB,得CD经过圆心O,连AO,由垂径定理得AD=1/2AB, 设圆形工件半径为r,OD=OC-CD=r-CD,在直角三角形AOD中,由勾股定理,求出r。
解、小亮的做法合理.
取AB=8 m,CD=2 m, 设圆形工件半径为r,
∴r2=(r-2)2+42. 得r=5(m).
14.解:连接OC,∵AB是直径,CD⊥AB,∴CP=CD=.在Rt△ACP中,AP==3,∴OP=AP-AO=3-AO=3-OC.在Rt△COP中,OC2=OP2+CP2,即OC2=(3-OC)2+.解得OC=2.∴OP=3-2=1.
15.解:连接OC,交AB于E.∵C是的中点,∴OC⊥AB,∴∠PEC=90°.作OF⊥CD,垂足为F,∴CF=CD=(cm).∵⊙O的直径是4 cm,∴OC=2 cm.在Rt△COF中,cosC=,∴∠C=30°,∴∠APC=90°-30°=60°.
16.解答: (1)证明:连接OC,
∵∠AOB=120°,C是AB弧的中点,
∴∠AOC=∠BOC=60°,
∵OA=OC,
∴△ACO是等边三角形,
∴OA=AC,同理OB=BC,
∴OA=AC=BC=OB,
∴四边形AOBC是菱形,
∴AB平分∠OAC;
(2)解:连接OC,
∵C为弧AB中点,∠AOB=120°,
∴∠AOC=60°,
∵OA=OC,
∴OAC是等边三角形,
∵OA=AC,
∴AP=AC,
∴∠APC=30°,
∴△OPC是直角三角形,
∴.
