北师大版九年级数学下第三章圆单元检测试题含答案
文档属性
| 名称 | 北师大版九年级数学下第三章圆单元检测试题含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 406.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-24 17:07:18 | ||
图片预览



文档简介
第三章 圆
一、选择题
1.如图3-198所示,弦AB的长为6 cm,圆心O到AB的距离为4 cm,则⊙O的半径为 ( )
A.3 cm B.4 cm C.5 cm D.6 cm
( http: / / www.21cnjy.com )
2.如图3-199所示,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠AOQ等于 ( )
A.60° B.65° C.72° D.75°
3.(2014年广西南宁,第6题3分)在直径为200cm的圆柱形油槽内装入一些油以后,截面如图.若油面的宽AB=160cm,则油的最大深度为( )
( http: / / www.21cnjy.com )
A. 40cm B. 60cm C. 80cm D. 100cm
4.如图3-201所示,AB,AC是⊙O的两条切线,B,C是切点.若∠A=70°,则∠BOC的度数为
A.130° B.120° C.110° D.100°
5.如图3-202所示,CD是⊙O的直径,A,B是⊙O上的两点.若∠ABD=20°,则∠ADC的度数为 ( )
A.40° B.50° C.60° D.70°
( http: / / www.21cnjy.com )
6.如图3-203所示,在梯形ABC ( http: / / www.21cnjy.com )D中,AB∥CD,AB⊥BC,AB=2 cm,CD=4 cm,以BC上一点O为圆心的圆经过A,D两点,且∠AOD=90°,则圆心O到弦AD的距离是 ( )
A.cm B.cm C.cm D.cm
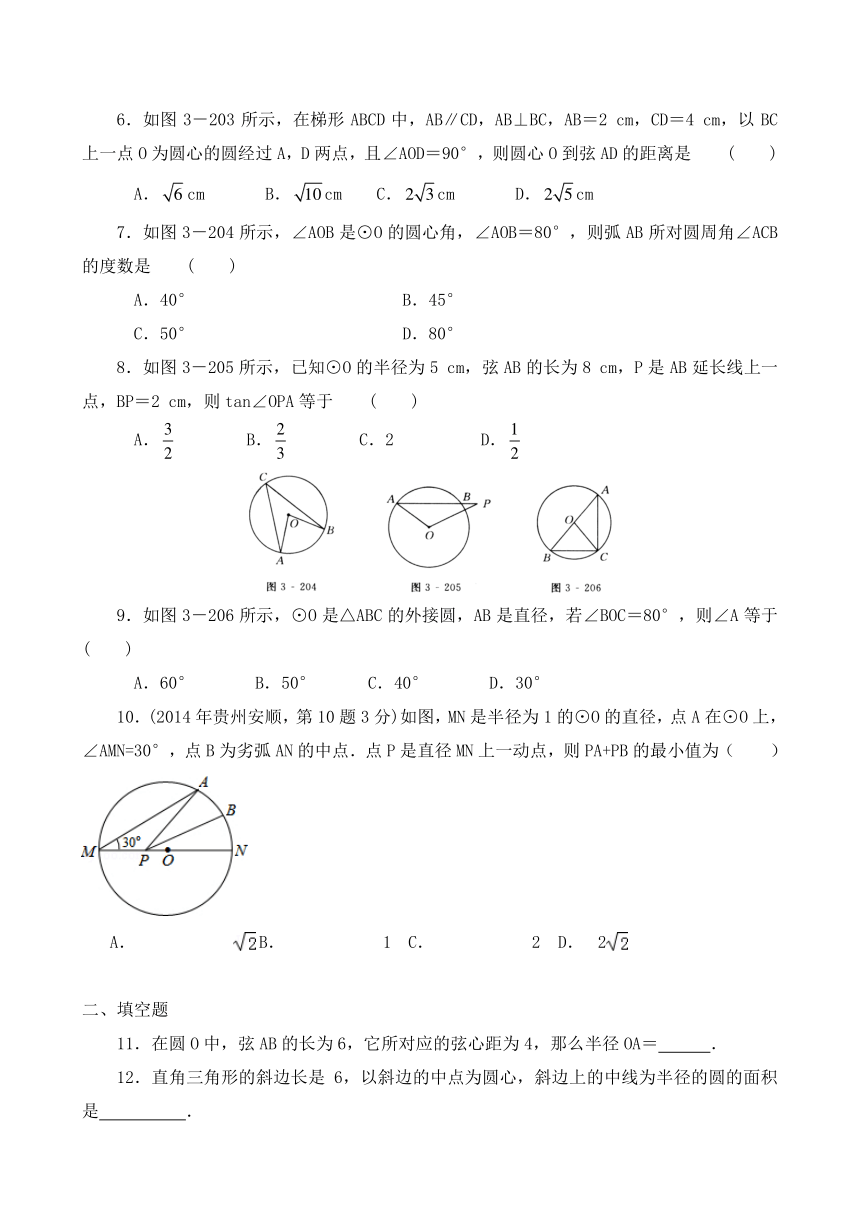
7.如图3-204所示,∠AOB是⊙O的圆心角,∠AOB=80°,则弧AB所对圆周角∠ACB的度数是 ( )
A.40° B.45°
C.50° D.80°
8.如图3-205所示,已知⊙O的半径为5 cm,弦AB的长为8 cm,P是AB延长线上一点,BP=2 cm,则tan∠OPA等于 ( )
A. B. C.2 D.
( http: / / www.21cnjy.com )
9.如图3-206所示,⊙O是△ABC的外接圆,AB是直径,若∠BOC=80°,则∠A等于 ( )
A.60° B.50° C.40° D.30°
10.(2014年贵州安顺,第10题3 ( http: / / www.21cnjy.com )分)如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,则PA+PB的最小值为( )
( http: / / www.21cnjy.com )
A. B. 1 C. 2 D. 2
二、填空题
11.在圆O中,弦AB的长为6,它所对应的弦心距为4,那么半径OA= .
12.直角三角形的斜边长是6,以斜边的中点为圆心,斜边上的中线为半径的圆的面积是 .
13.(2014 广西来宾,第18题3分)如图,点A、B、C均在⊙O上,∠C=50°,则∠OAB= 度.
( http: / / www.21cnjy.com ).
14.如图3-207所示,AB是⊙O的直径,弦CD∥AB.若∠ABD=65°,则∠ADC= .
( http: / / www.21cnjy.com )
15.如图3-208所示,在⊙O中,直径MN=10,正方形ABCD的四个顶点分别在PM以及⊙O的半径OM,OP上,并且∠POM=45°,则AB的长为 .
16.如图3-209所示,⊙A,⊙B的 ( http: / / www.21cnjy.com )圆心A,B在直线l上,两圆的半径都为1 cm,开始时圆心距AB=4 cm.现⊙A,⊙B同时沿直线l以每秒2 cm的速度相向移动,则当两圆相切时,⊙A运动的时间为 秒.
17.(2014 黔南州,第19题5分)如图,直径为10的⊙A经过点C(0,6)和点O(0,0),与x轴的正半轴交于点D,B是y轴右侧圆弧上一点,则cos∠OBC的值为 .
( http: / / www.21cnjy.com )
18.如图3-210所示, ( http: / / www.21cnjy.com )点A,B是⊙O上两点,AB=10,点P是⊙O上的动点(P与A,B不重合),连接AP,PB,过点O分别作OE⊥AP于E,OF⊥PB于F,则EF= .
( http: / / www.21cnjy.com )
19.如图3-211所示,把半径为4 ( http: / / www.21cnjy.com )cm的半圆围成一个圆锥的侧面,使半圆圆心为圆锥的顶点,那么这个圆锥的高是 cm.(结果保留根号)
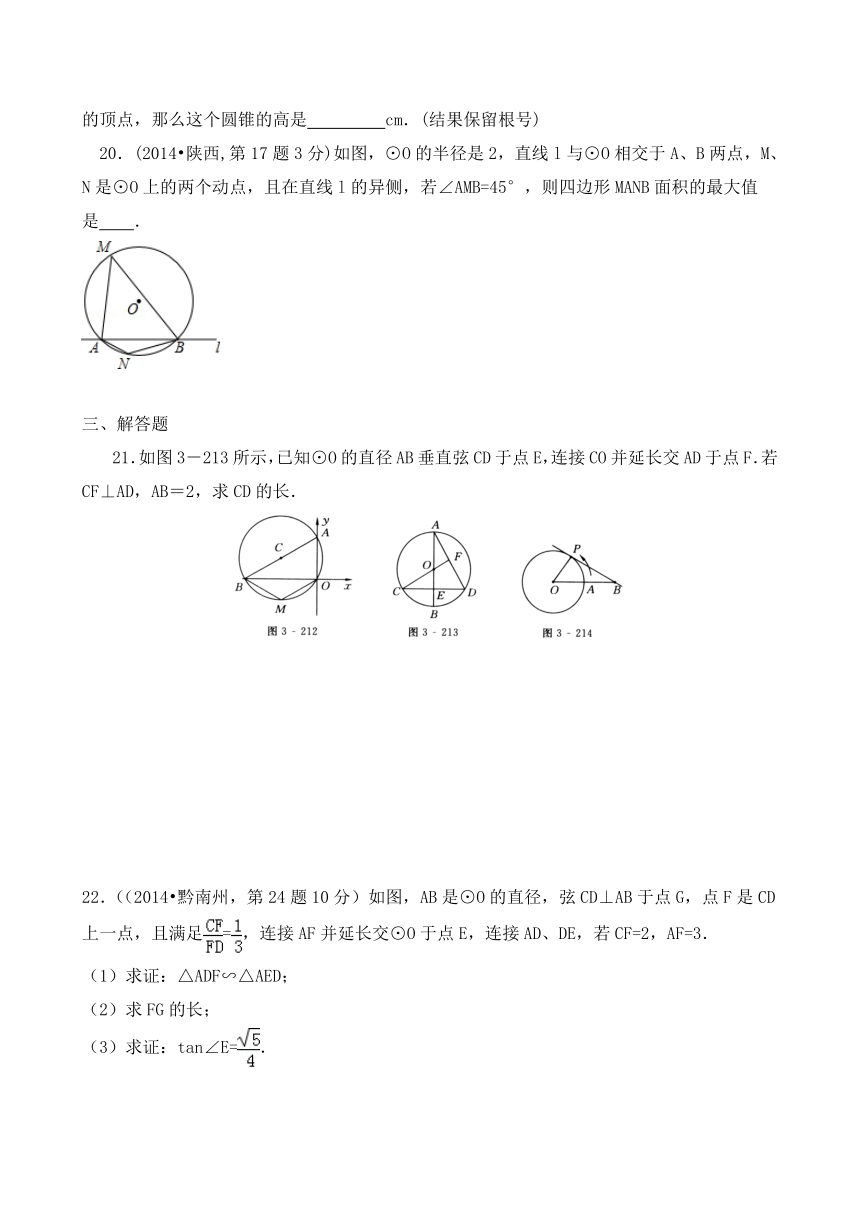
20.(2014 陕西,第17题3分)如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是 .
( http: / / www.21cnjy.com )
三、解答题
21.如图3-213所示,已知⊙O的直径AB垂直弦CD于点E,连接CO并延长交AD于点F.若CF⊥AD,AB=2,求CD的长.
( http: / / www.21cnjy.com )
22.((2014 黔南州,第24题10分)如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足=,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.
(1)求证:△ADF∽△AED;
(2)求FG的长;
(3)求证:tan∠E=.
( http: / / www.21cnjy.com )
23.如图3-215所示,已知△ABC内接于⊙O,点D在OC的延长线上,sin B=,∠D=30°.
(1)求证AD是⊙O的切线;
(2)若AC=6,求AD的长.
24.如图3-216所示,AB是⊙O的直径,弦BC=5,∠BOC=50°,OE⊥AC,垂足为E.
(1)求OE的长;
(2)求劣弧AC的长.(结果精确到0.1)
( http: / / www.21cnjy.com )
25.(2014 湖北黄石,第19题7分)如图,A、B是圆O上的两点,∠AOB=120°,C是AB弧的中点.
(1)求证:AB平分∠OAC;
(2)延长OA至P使得OA=AP,连接PC,若圆O的半径R=1,求PC的长.
( http: / / www.21cnjy.com )
26.如图3-218(1)所示,圆内接△ABC中,AB=BC=CA,OD,OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G.
(1)求证阴影部分四边形OFCG的面积是△ABC面积的;
(2)如图3-218(2)所示,若∠DOE保持120°角度不变,求证当∠DOE绕着O点旋转时,由两条半径和△ABC的两条边围成的图形(图中阴影部分)面积始终是△ABC的面积的.
( http: / / www.21cnjy.com )
参考答案
1.C 2.D 3.A 4.C 5.D 6.B 7.A 8.D 9.C 10.AB 11.5 12.9π 13.40 14.25° 15. 16.或 17. 18.5 19.
20.4.
21.解:如图3-219所示,在△AOF和△COE中.∠AFO=∠CEO=90°,∠AOF=∠COE,∴∠A=∠C.连接OD,则∠A=∠ODA,∠C=∠ODC,∴∠A=∠ODA=∠ODC.∵∠A+∠ODA+∠ODC=90°,∴∠ODC=30°,∴DE=ODcos 30°=.CD=2DE=.
22.解:①∵AB是⊙O的直径,弦CD⊥AB,
∴DG=CG,
∴弧AD=弧AC,∠ADF=∠AED,
∵∠FAD=∠DAE(公共角),
∴△ADF∽△AED;
②∵=,CF=2,
∴FD=6,
∴CD=DF+CF=8,
∴CG=DG=4,
∴FG=CG﹣CF=2;
③∵AF=3,FG=2,
③∵AF=3,FG=2,∴AG=,
tan∠E=.
( http: / / www.21cnjy.com )
23.(1)证明:如图3-221所示,连接OA.∵sin B=,∴∠B=30°,∴∠AOC=60°.∵∠D=30°,∴∠OAD=180°-∠D-∠AOD=90°.∴AD是⊙O的切线. (2)解:∵OA=OC,∠AOC=60°,∴△AOC是等边三角形.∴OA=AC=6.∵∠OAD=90°,∠D=30°,∴AD=.
24.解:(1)∵OE⊥AC.垂足为E.∴AE=EC.∵AO=BO,∴OE=BC=.(2)∠A=∠BOC=25°,在Rt△AOE中,∵sin A=,∴ OA=.∵∠AOC=180°-50°=130°, ∴劣弧AC的长=≈13.4.
25.
解答: (1)证明:连接OC,
∵∠AOB=120°,C是AB弧的中点,
∴∠AOC=∠BOC=60°,
∵OA=OC,
∴△ACO是等边三角形,
∴OA=AC,同理OB=BC,
∴OA=AC=BC=OB,
∴四边形AOBC是菱形,
∴AB平分∠OAC;
(2)解:连接OC,
∵C为弧AB中点,∠AOB=120°,
∴∠AOC=60°,
∵OA=OC,
∴OAC是等边三角形,
∵OA=AC,
∴AP=AC,
∴∠APC=30°,
∴△OPC是直角三角形,
∴.
( http: / / www.21cnjy.com )
26.(1)证明:连接OA,OC,∵点O是等边三角形ABC的外心,Rt△OFC≌Rt△OGC≌Rt△OGA,S四边形OFCG=2S△OFC=S△OAC.∵S△OAC=S△ABC,∴S四边形OFCG=S△ABC. (2)证法1:如图3-223(1)所示,连接OA,OB和OC,则△AOC≌△COB≌△BOA,∠1=∠2.不妨设OD交BC于点F,OE交AC于点G,∠AOC=∠3+∠4=120°,∠DOE=∠5+∠4=120°,∴∠3=∠5.在△OAG和△OCF中,∴△OAG≌△OCF,∴S四边形OFCG=S△AOC=S△ABC.证法2:如图3-223(2)所示,不妨设OD交BC于点F,OE交AC于点G,作DH⊥BC,OK⊥AC,垂足分别为点H,K.在四边形HOKC中,∠OHC=∠OKC=90°,∠C=60°,∴∠HOK=360°-90°-90°-60°=120°,即∠1+∠2=120°.又∵∠GOF=∠2+∠3=120°∴∠1=∠3.∵AC=BC,∴OH=OK.又∠OHF=∠OKG=90°.∴△OFH≌△OGK,∴S四边形OFCG=S四边形OHCK=S△ABC.
( http: / / www.21cnjy.com )
一、选择题
1.如图3-198所示,弦AB的长为6 cm,圆心O到AB的距离为4 cm,则⊙O的半径为 ( )
A.3 cm B.4 cm C.5 cm D.6 cm
( http: / / www.21cnjy.com )
2.如图3-199所示,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠AOQ等于 ( )
A.60° B.65° C.72° D.75°
3.(2014年广西南宁,第6题3分)在直径为200cm的圆柱形油槽内装入一些油以后,截面如图.若油面的宽AB=160cm,则油的最大深度为( )
( http: / / www.21cnjy.com )
A. 40cm B. 60cm C. 80cm D. 100cm
4.如图3-201所示,AB,AC是⊙O的两条切线,B,C是切点.若∠A=70°,则∠BOC的度数为
A.130° B.120° C.110° D.100°
5.如图3-202所示,CD是⊙O的直径,A,B是⊙O上的两点.若∠ABD=20°,则∠ADC的度数为 ( )
A.40° B.50° C.60° D.70°
( http: / / www.21cnjy.com )
6.如图3-203所示,在梯形ABC ( http: / / www.21cnjy.com )D中,AB∥CD,AB⊥BC,AB=2 cm,CD=4 cm,以BC上一点O为圆心的圆经过A,D两点,且∠AOD=90°,则圆心O到弦AD的距离是 ( )
A.cm B.cm C.cm D.cm
7.如图3-204所示,∠AOB是⊙O的圆心角,∠AOB=80°,则弧AB所对圆周角∠ACB的度数是 ( )
A.40° B.45°
C.50° D.80°
8.如图3-205所示,已知⊙O的半径为5 cm,弦AB的长为8 cm,P是AB延长线上一点,BP=2 cm,则tan∠OPA等于 ( )
A. B. C.2 D.
( http: / / www.21cnjy.com )
9.如图3-206所示,⊙O是△ABC的外接圆,AB是直径,若∠BOC=80°,则∠A等于 ( )
A.60° B.50° C.40° D.30°
10.(2014年贵州安顺,第10题3 ( http: / / www.21cnjy.com )分)如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,则PA+PB的最小值为( )
( http: / / www.21cnjy.com )
A. B. 1 C. 2 D. 2
二、填空题
11.在圆O中,弦AB的长为6,它所对应的弦心距为4,那么半径OA= .
12.直角三角形的斜边长是6,以斜边的中点为圆心,斜边上的中线为半径的圆的面积是 .
13.(2014 广西来宾,第18题3分)如图,点A、B、C均在⊙O上,∠C=50°,则∠OAB= 度.
( http: / / www.21cnjy.com ).
14.如图3-207所示,AB是⊙O的直径,弦CD∥AB.若∠ABD=65°,则∠ADC= .
( http: / / www.21cnjy.com )
15.如图3-208所示,在⊙O中,直径MN=10,正方形ABCD的四个顶点分别在PM以及⊙O的半径OM,OP上,并且∠POM=45°,则AB的长为 .
16.如图3-209所示,⊙A,⊙B的 ( http: / / www.21cnjy.com )圆心A,B在直线l上,两圆的半径都为1 cm,开始时圆心距AB=4 cm.现⊙A,⊙B同时沿直线l以每秒2 cm的速度相向移动,则当两圆相切时,⊙A运动的时间为 秒.
17.(2014 黔南州,第19题5分)如图,直径为10的⊙A经过点C(0,6)和点O(0,0),与x轴的正半轴交于点D,B是y轴右侧圆弧上一点,则cos∠OBC的值为 .
( http: / / www.21cnjy.com )
18.如图3-210所示, ( http: / / www.21cnjy.com )点A,B是⊙O上两点,AB=10,点P是⊙O上的动点(P与A,B不重合),连接AP,PB,过点O分别作OE⊥AP于E,OF⊥PB于F,则EF= .
( http: / / www.21cnjy.com )
19.如图3-211所示,把半径为4 ( http: / / www.21cnjy.com )cm的半圆围成一个圆锥的侧面,使半圆圆心为圆锥的顶点,那么这个圆锥的高是 cm.(结果保留根号)
20.(2014 陕西,第17题3分)如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是 .
( http: / / www.21cnjy.com )
三、解答题
21.如图3-213所示,已知⊙O的直径AB垂直弦CD于点E,连接CO并延长交AD于点F.若CF⊥AD,AB=2,求CD的长.
( http: / / www.21cnjy.com )
22.((2014 黔南州,第24题10分)如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足=,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.
(1)求证:△ADF∽△AED;
(2)求FG的长;
(3)求证:tan∠E=.
( http: / / www.21cnjy.com )
23.如图3-215所示,已知△ABC内接于⊙O,点D在OC的延长线上,sin B=,∠D=30°.
(1)求证AD是⊙O的切线;
(2)若AC=6,求AD的长.
24.如图3-216所示,AB是⊙O的直径,弦BC=5,∠BOC=50°,OE⊥AC,垂足为E.
(1)求OE的长;
(2)求劣弧AC的长.(结果精确到0.1)
( http: / / www.21cnjy.com )
25.(2014 湖北黄石,第19题7分)如图,A、B是圆O上的两点,∠AOB=120°,C是AB弧的中点.
(1)求证:AB平分∠OAC;
(2)延长OA至P使得OA=AP,连接PC,若圆O的半径R=1,求PC的长.
( http: / / www.21cnjy.com )
26.如图3-218(1)所示,圆内接△ABC中,AB=BC=CA,OD,OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G.
(1)求证阴影部分四边形OFCG的面积是△ABC面积的;
(2)如图3-218(2)所示,若∠DOE保持120°角度不变,求证当∠DOE绕着O点旋转时,由两条半径和△ABC的两条边围成的图形(图中阴影部分)面积始终是△ABC的面积的.
( http: / / www.21cnjy.com )
参考答案
1.C 2.D 3.A 4.C 5.D 6.B 7.A 8.D 9.C 10.AB 11.5 12.9π 13.40 14.25° 15. 16.或 17. 18.5 19.
20.4.
21.解:如图3-219所示,在△AOF和△COE中.∠AFO=∠CEO=90°,∠AOF=∠COE,∴∠A=∠C.连接OD,则∠A=∠ODA,∠C=∠ODC,∴∠A=∠ODA=∠ODC.∵∠A+∠ODA+∠ODC=90°,∴∠ODC=30°,∴DE=ODcos 30°=.CD=2DE=.
22.解:①∵AB是⊙O的直径,弦CD⊥AB,
∴DG=CG,
∴弧AD=弧AC,∠ADF=∠AED,
∵∠FAD=∠DAE(公共角),
∴△ADF∽△AED;
②∵=,CF=2,
∴FD=6,
∴CD=DF+CF=8,
∴CG=DG=4,
∴FG=CG﹣CF=2;
③∵AF=3,FG=2,
③∵AF=3,FG=2,∴AG=,
tan∠E=.
( http: / / www.21cnjy.com )
23.(1)证明:如图3-221所示,连接OA.∵sin B=,∴∠B=30°,∴∠AOC=60°.∵∠D=30°,∴∠OAD=180°-∠D-∠AOD=90°.∴AD是⊙O的切线. (2)解:∵OA=OC,∠AOC=60°,∴△AOC是等边三角形.∴OA=AC=6.∵∠OAD=90°,∠D=30°,∴AD=.
24.解:(1)∵OE⊥AC.垂足为E.∴AE=EC.∵AO=BO,∴OE=BC=.(2)∠A=∠BOC=25°,在Rt△AOE中,∵sin A=,∴ OA=.∵∠AOC=180°-50°=130°, ∴劣弧AC的长=≈13.4.
25.
解答: (1)证明:连接OC,
∵∠AOB=120°,C是AB弧的中点,
∴∠AOC=∠BOC=60°,
∵OA=OC,
∴△ACO是等边三角形,
∴OA=AC,同理OB=BC,
∴OA=AC=BC=OB,
∴四边形AOBC是菱形,
∴AB平分∠OAC;
(2)解:连接OC,
∵C为弧AB中点,∠AOB=120°,
∴∠AOC=60°,
∵OA=OC,
∴OAC是等边三角形,
∵OA=AC,
∴AP=AC,
∴∠APC=30°,
∴△OPC是直角三角形,
∴.
( http: / / www.21cnjy.com )
26.(1)证明:连接OA,OC,∵点O是等边三角形ABC的外心,Rt△OFC≌Rt△OGC≌Rt△OGA,S四边形OFCG=2S△OFC=S△OAC.∵S△OAC=S△ABC,∴S四边形OFCG=S△ABC. (2)证法1:如图3-223(1)所示,连接OA,OB和OC,则△AOC≌△COB≌△BOA,∠1=∠2.不妨设OD交BC于点F,OE交AC于点G,∠AOC=∠3+∠4=120°,∠DOE=∠5+∠4=120°,∴∠3=∠5.在△OAG和△OCF中,∴△OAG≌△OCF,∴S四边形OFCG=S△AOC=S△ABC.证法2:如图3-223(2)所示,不妨设OD交BC于点F,OE交AC于点G,作DH⊥BC,OK⊥AC,垂足分别为点H,K.在四边形HOKC中,∠OHC=∠OKC=90°,∠C=60°,∴∠HOK=360°-90°-90°-60°=120°,即∠1+∠2=120°.又∵∠GOF=∠2+∠3=120°∴∠1=∠3.∵AC=BC,∴OH=OK.又∠OHF=∠OKG=90°.∴△OFH≌△OGK,∴S四边形OFCG=S四边形OHCK=S△ABC.
( http: / / www.21cnjy.com )
