人教版六年级数学下册4.15.整理和复习课件(共42张PPT)
文档属性
| 名称 | 人教版六年级数学下册4.15.整理和复习课件(共42张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-10 21:42:59 | ||
图片预览







文档简介
(共42张PPT)
R·六年级下册
整理和复习
请同学们先回忆本单元的学习内容,结合前面学习的整理方式,对本单元进行梳理。
知识回顾与梳理
表格整理
思维导图
知识框架
文字、公式、图示……
条理清晰,层次分明,
体现知识间的联系与区别。
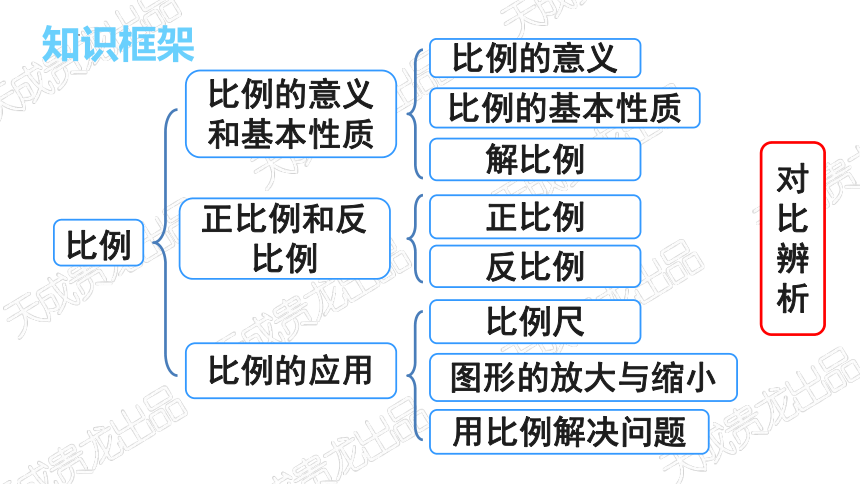
知识框架
比例
比例的意义和基本性质
正比例和反比例
比例的应用
比例的意义
比例的基本性质
解比例
正比例
反比例
比例尺
图形的放大与缩小
用比例解决问题
对比辨析
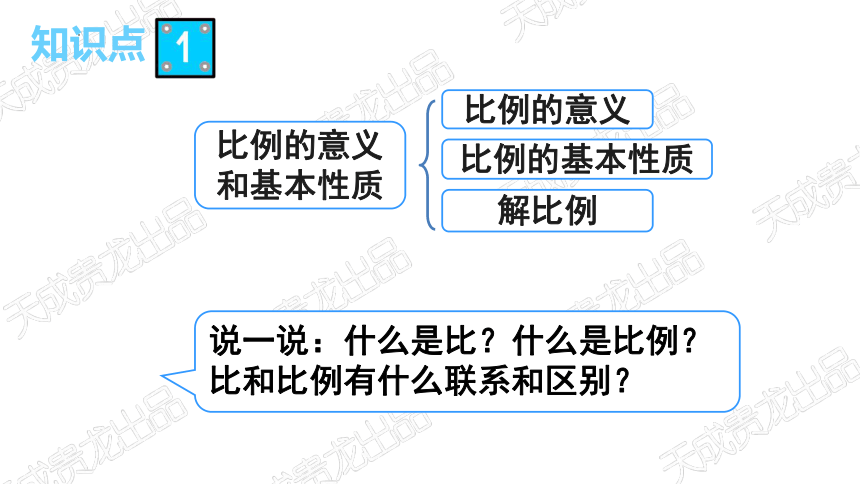
比例的意义和基本性质
比例的意义
比例的基本性质
解比例
说一说:什么是比?什么是比例?比和比例有什么联系和区别?
知识点
比 比例
意义
各部分 名称
基本 性质
前项
后项
比值
外项
内项
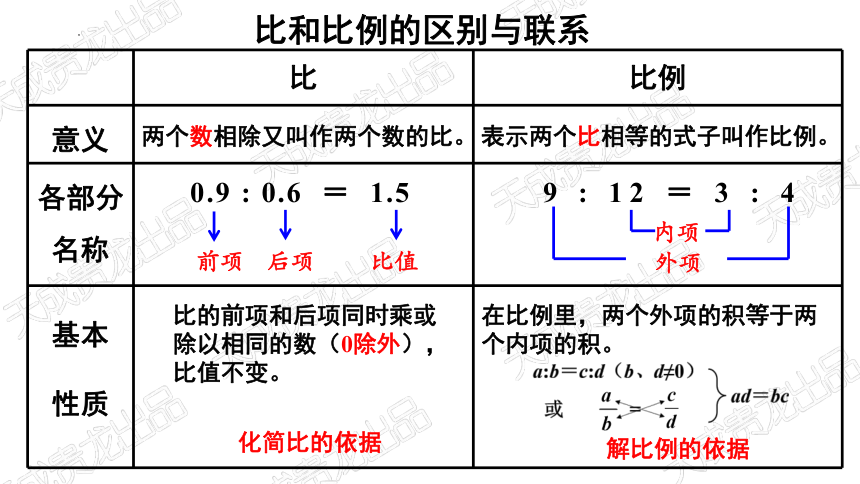
两个数相除又叫作两个数的比。
表示两个比相等的式子叫作比例。
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
在比例里,两个外项的积等于两个内项的积。
比和比例的区别与联系
0.9 : 0.6 = 1.5
9 : 12 = 3 : 4
化简比的依据
解比例的依据
辨析练习
1. 判断下面哪组中的两个比可以组成比例。
6 ∶3 和 8 ∶5
0.2∶ 和 4∶50
6∶3=2 8∶5=1.6
2≠1.6,所以6∶3≠8∶5,不可以组成比例。
0.2∶ =0.08 4∶50=0.08
0.08=0.08,所以0.2∶ = 4∶50,可以组成比例。
2. 大小两个圆的半径之比是5:3。它们的直径之比是
( ),周长之比是( ),面积之比是( )。
R:r=5:3
D:d=2R:2r=5:3
C:c=πD:πd=5:3
S:s=πR :πr = 5 :3 =25:9
r
R
d
D
c
C
=
=
s
S
=
r
R
5:3
5:3
25:9
3. 两个长方形面积相等,你能根据它们边之间的关系
写出一些比例吗?
a
b
16
10
a×16 = b×10
a:b=10:16 16:b=10:a
b:a=16:10 10:a=16:b
a:10=b:16 16:10=b:a
b:16=a:10 10:16=a:b
4.解比例的依据是什么?解下面的比例。
6.5∶x=3.25∶4
解:5x=4×6
x=4.8
解:1.2x=3×2.5
x=6.25
解:3.25x=6.5×4
x=8
x=4.8
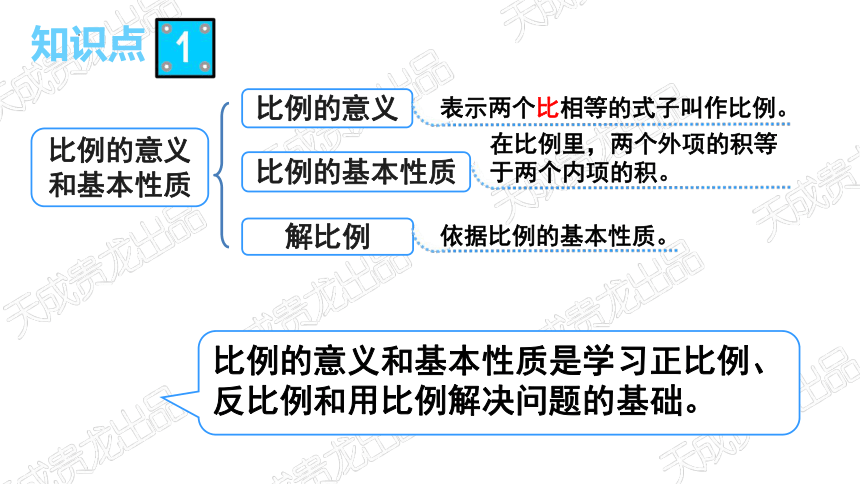
比例的意义和基本性质
比例的意义
比例的基本性质
解比例
比例的意义和基本性质是学习正比例、反比例和用比例解决问题的基础。
知识点
表示两个比相等的式子叫作比例。
在比例里,两个外项的积等于两个内项的积。
依据比例的基本性质。
知识点
正比例和反比例
正比例
反比例
下面每个表中的两个量,哪些成比例关系?成正比例关系还是反比例关系?哪些不成比例关系?
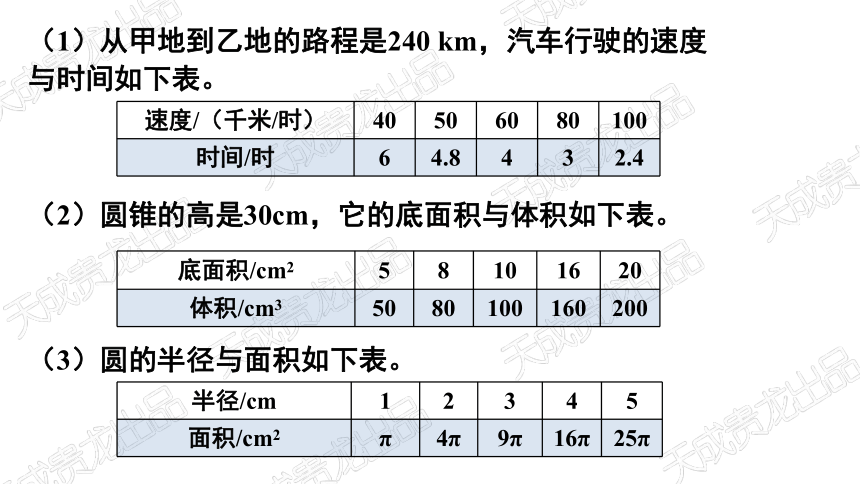
(1)从甲地到乙地的路程是240 km,汽车行驶的速度与时间如下表。
速度/(千米/时) 40 50 60 80 100
时间/时 6 4.8 4 3 2.4
(2)圆锥的高是30cm,它的底面积与体积如下表。
底面积/cm2 5 8 10 16 20
体积/cm3 50 80 100 160 200
(3)圆的半径与面积如下表。
半径/cm 1 2 3 4 5
面积/cm2 π 4π 9π 16π 25π
(1)从甲地到乙地的路程是240 km,汽车行驶的速度与时间如下表。
速度/(千米/时) 40 50 60 80 100
时间/时 6 4.8 4 3 2.4
速度×时间=路程
(一定)
路程/(千米) 240 240 240 240 240
反比例
(2)圆锥的高是30cm,它的底面积与体积如下表。
底面积/cm2 5 8 10 16 20
体积/cm3 50 80 100 160 200
圆锥的体积÷底面积= 高
高 /cm 10 10 10 10 10
(一定)
正比例
(3)圆的半径与面积如下表。
半径/cm 1 2 3 4 5
面积/cm2 π 4π 9π 16π 25π
=圆周率×半径
(变量)
不成比例
圆周率×半径 π 2π 3π 4π 5π
(1)从甲地到乙地的路程是240 km,汽车行驶的速度与时间如下表。
速度/(千米/时) 40 50 60 80 100
时间/时 6 4.8 4 3 2.4
(2)圆锥的高是30cm,它的体积与底面积如下表。
底面积/cm2 5 8 10 16 20
体积/cm3 50 80 100 160 200
反比例
正比例
说一说:正比例和反比例有什么联系与区别呢?
正比例 反比例
正比例和反比例的异同点
都有两种相关联的量,一种量变化,另一种量也随着变化。
两种量“变化方向”相同
两种量“变化方向”相反
相同点
不同点
相对应的两个量的比值(商)一定
相对应的两个量的乘积一定
x
y
= k
(一定)
关系式:
关系式:
xy=k(一定)
正比例关系图象是一条射线
反比例关系图象是一条曲线
知识点
这是判断两个量是否成正比例或反比例关系的关键。
正比例和反比例
正比例
反比例
两种相关联的量的比值一定。
两种相关联的量的乘积一定。
利用比例的知识可以解决生活中哪些实际问题呢?
知识点
比例的应用
比例尺
图形的放大与缩小
用比例解决问题
放大比例尺
01
比例尺
1. 一幅地图中某两地的图上距离5cm表示实际距离15km,这幅图的比例尺是( )。
1∶300000
图上距离:实际距离=比例尺
图上距离:实际距离
=5cm∶15km
=5cm∶1500000cm
5cm与15km的长度单位不同,先统一单位。
一幅图的图上距离和实际距离的比,叫作这幅图的比例尺。
=1∶300000
1∶300000
1
300000
数值比例尺
或
线段比例尺
2∶1
缩小比例尺
3km
2. 5号线是郑州市地铁线网规划中唯一的环线地铁,全长大约40.4 km。在比例尺为 1∶20000 的37寸LED动态地图上,5号线长多少厘米?
解:设5号线的图上距离是 x cm。
解比例
40.4 km = 4040000 cm
4040000
x
=
1
20000
x=202
4040000×
1
20000
=202(cm)
答:5号线长 202 cm。
辨析练习
3.小华和小强分别将学校的花坛画了下来,如下图。如果小华是按1∶a的比例尺画的,那么小强是按( )的比例尺画的。
辨析练习
A. 1∶ a B. 1∶2a C. 1∶a D. 1∶ a
B
02
图形的放大与缩小
1. 把一个长5cm、宽3cm的长方形按3∶1放大,得到的图形的面积是( )cm 。
135
长5cm
宽3cm
放大后长15cm
放大后宽9cm
15 × 9 =135(cm )
5 × 3 = 15(cm )
×3
×3
×3
2. 把一个长15cm、宽9cm的长方形按1∶3缩小,得到的图形的面积是( )cm 。
15
长15cm
宽9cm
缩小后长5cm
缩小后宽3cm
15 × 9 =135(cm )
5 × 3 = 15(cm )
÷3
÷3
÷3
辨析练习
2. 把一个长15cm、宽9cm的长方形按1∶3缩小,得到的图形的面积是( )cm 。
15
长15cm
宽9cm
缩小后长5cm
缩小后宽3cm
图形的大小变了,但形状不变。
一个图形放大到原来的n倍或缩小到原来的 (n不为0),它的面积就放大到原来的n 倍或缩小到原来的 。
n
1
n
1
辨析练习
2. 把一个长15cm、宽9cm的长方形按1∶3缩小,得到的图形的面积是( )cm 。
15
长15cm
宽9cm
缩小后长5cm
缩小后宽3cm
画图方法:
一厘,厘清要求。
二算,计算边长。
三画,画出图形。
图形的大小变了,但形状不变。
辨析练习
图形放大
图形缩小
3 : 1
1 : 3
放大或缩小
的图形
原来图形
放大比例尺
一幅零件图纸的
比例尺是2:1
缩小比例尺
这幅地图的比例尺是1:300000
图上距离
实际距离
∶
∶
说一说:图形放大与缩小和比例尺有什么联系与区别呢?
比例尺
图形的放大与缩小
1. 李叔叔开车从甲地到乙地,前2小时行驶了100km。照这样的速度,从甲地到乙地一共要用3小时,甲乙两地相距多远?
03
用比例解决问题
2. 李叔叔开车从甲地到乙地一共用了3小时,每小时行驶50km。原路返回时每小时行驶60km,返回时用了多长时间?
解:设甲乙两地相距 x km。
3
x
=
100
2
x=150
解:设返回时用了x小时。
60x=3×50
x=2.5
答:甲乙两地相距150km。
答:返回时用了2.5小时。
辨析练习
1. 李叔叔开车从甲地到乙地,前2小时行驶了100km。照这样的速度,从甲地到乙地一共要用3小时,甲乙两地相距多远?
2. 李叔叔开车从甲地到乙地一共用了3小时,每小时行驶50km。原路返回时每小时行驶60km,返回时用了多长时间?
1. 李叔叔开车从甲地到乙地,前2小时行驶了100km。照这样的速度,从甲地到乙地一共要用3小时,甲乙两地相距多远?
2. 李叔叔开车从甲地到乙地一共用了3小时,每小时行驶50km。原路返回时每小时行驶60km,返回时用了多长时间?
01
找到题目中的不变量
辨析练习
路程÷时间=速度(一定)
速度×时间=路程(一定)
02
看哪两种量成比例关系
03
根据比例关系写出关系式
04
解方程并检验作答
正比例
反比例
知识点
比例的应用
比例尺
图形的放大与缩小
用比例解决问题
厘清相关联量之间的关系,灵活运用多种知识,才能不断提高解决问题的能力。
比例尺是一个比。
图上距离∶实际距离=比例尺
图形放大或缩小后,
形状相同,大小不同。
要正确判断相关联的两个量成什么比例关系。
比例
知识框架
综合运用
1.下面各题中的两种量之间是否有比例关系?如果有,成什么比例关系 ?
(1)比例尺一定,两地的实际距离和图上距离。
(2)积(0除外)一定,一个因数和另一个因数。
(3)梯形的上底和下底不变,梯形的面积和高。
(4)如果y=5x,y和x。
图上距离∶实际距离=比例尺(一定)
一个因数×另一个因数=积(一定)
梯形的面积÷高=(上底+下底)÷2(一定)
y÷x=5
正比例
反比例
正比例
正比例
2. 在一副比例尺是 1∶2000000 的地图上,量得甲、乙
两个城市之间的距离是 5.5 cm。在另一幅比例尺
是 1∶5000000 的地图上,这两个城市之间的图上
距离是多少?
解:设甲、乙两个城市之间的实际距离是 x cm。
x
2000000
1
=
5.5
x=11000000
解:设甲、乙两个城市之间的实际距离是 x cm。
x
5000000
1
=
11000000
x=2.2cm
答:这两个城市之间的图上距离是2.2cm。
2. 在一幅比例尺是 1∶2000000 的地图上,量得甲、乙
两个城市之间的距离是 5.5 cm。在另一幅比例尺
是 1∶5000000 的地图上,这两个城市之间的图上
距离是多少?
5
5.5×
2
=2.2(cm)
答:这两个城市之间的图上距离是 2.2 cm。
5000000
1
÷
5
2000000
1
=
2
3*. 一个服装店的所有服装都按同样的折扣销售。
(1)李阿姨买了一件上衣,原价250元,现价150元。李阿姨还想买一条裤子,原价180元,现价多少钱?
(2)张叔叔带的钱,如果买现价90元一件的衬衫,正好可以买4件。如果买原价200元一件的夹克衫,能买多少件?
(3)如果用x表示原价,y表示现价,y和x的关系式为________。
现价÷原价=折扣(一定)
正比例
(1)李阿姨买了一件上衣,原价250元,现价150元。李阿姨还想买一条裤子,原价180元,现价多少钱?
解:设现价x元。
180
250
150
=
x
250x=150×180
x=108
答:现价108元。
现价÷原价=折扣(一定)
正比例
3*. 一个服装店的所有服装都按同样的折扣销售。
(2)张叔叔带钱,如果买现价90元一件的衬衫,正好可以买4件。如果买原价200元一件的夹克衫,能买多少件?
单价×数量=总价(一定)
反比例
解:设能买x件。
90×4=200×
250
150
×x
120x=360
x=3
答:能买3件。
现在单价多少钱?
3*. 一个服装店的所有服装都按同样的折扣销售。
(1)李阿姨买了一件上衣,原价250元,现价150元。李阿姨还想买一条裤子,原价180元,现价多少钱?
(2)张叔叔带的钱,如果买现价90元一件的衬衫,正好可以买4件。如果买原价200元一件的夹克衫,能买多少件?
(3)如果用x表示原价,y表示现价,y和x的关系式为________。
y=60%x
现价÷原价=折扣(一定)
折扣=现价÷原价=150÷250=0.6
y ÷ x = ?
或y=0.6x
3*. 一个服装店的所有服装都按同样的折扣销售。
解决问题的方法
算术方法
方程
比例
我们解决生活中实际问题的策略和方法越发多样化了。厘清关系,灵活运用,才能不断提高解决问题的能力。
课后作业
完成本课时的相关习题。
谢 谢!
R·六年级下册
整理和复习
请同学们先回忆本单元的学习内容,结合前面学习的整理方式,对本单元进行梳理。
知识回顾与梳理
表格整理
思维导图
知识框架
文字、公式、图示……
条理清晰,层次分明,
体现知识间的联系与区别。
知识框架
比例
比例的意义和基本性质
正比例和反比例
比例的应用
比例的意义
比例的基本性质
解比例
正比例
反比例
比例尺
图形的放大与缩小
用比例解决问题
对比辨析
比例的意义和基本性质
比例的意义
比例的基本性质
解比例
说一说:什么是比?什么是比例?比和比例有什么联系和区别?
知识点
比 比例
意义
各部分 名称
基本 性质
前项
后项
比值
外项
内项
两个数相除又叫作两个数的比。
表示两个比相等的式子叫作比例。
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
在比例里,两个外项的积等于两个内项的积。
比和比例的区别与联系
0.9 : 0.6 = 1.5
9 : 12 = 3 : 4
化简比的依据
解比例的依据
辨析练习
1. 判断下面哪组中的两个比可以组成比例。
6 ∶3 和 8 ∶5
0.2∶ 和 4∶50
6∶3=2 8∶5=1.6
2≠1.6,所以6∶3≠8∶5,不可以组成比例。
0.2∶ =0.08 4∶50=0.08
0.08=0.08,所以0.2∶ = 4∶50,可以组成比例。
2. 大小两个圆的半径之比是5:3。它们的直径之比是
( ),周长之比是( ),面积之比是( )。
R:r=5:3
D:d=2R:2r=5:3
C:c=πD:πd=5:3
S:s=πR :πr = 5 :3 =25:9
r
R
d
D
c
C
=
=
s
S
=
r
R
5:3
5:3
25:9
3. 两个长方形面积相等,你能根据它们边之间的关系
写出一些比例吗?
a
b
16
10
a×16 = b×10
a:b=10:16 16:b=10:a
b:a=16:10 10:a=16:b
a:10=b:16 16:10=b:a
b:16=a:10 10:16=a:b
4.解比例的依据是什么?解下面的比例。
6.5∶x=3.25∶4
解:5x=4×6
x=4.8
解:1.2x=3×2.5
x=6.25
解:3.25x=6.5×4
x=8
x=4.8
比例的意义和基本性质
比例的意义
比例的基本性质
解比例
比例的意义和基本性质是学习正比例、反比例和用比例解决问题的基础。
知识点
表示两个比相等的式子叫作比例。
在比例里,两个外项的积等于两个内项的积。
依据比例的基本性质。
知识点
正比例和反比例
正比例
反比例
下面每个表中的两个量,哪些成比例关系?成正比例关系还是反比例关系?哪些不成比例关系?
(1)从甲地到乙地的路程是240 km,汽车行驶的速度与时间如下表。
速度/(千米/时) 40 50 60 80 100
时间/时 6 4.8 4 3 2.4
(2)圆锥的高是30cm,它的底面积与体积如下表。
底面积/cm2 5 8 10 16 20
体积/cm3 50 80 100 160 200
(3)圆的半径与面积如下表。
半径/cm 1 2 3 4 5
面积/cm2 π 4π 9π 16π 25π
(1)从甲地到乙地的路程是240 km,汽车行驶的速度与时间如下表。
速度/(千米/时) 40 50 60 80 100
时间/时 6 4.8 4 3 2.4
速度×时间=路程
(一定)
路程/(千米) 240 240 240 240 240
反比例
(2)圆锥的高是30cm,它的底面积与体积如下表。
底面积/cm2 5 8 10 16 20
体积/cm3 50 80 100 160 200
圆锥的体积÷底面积= 高
高 /cm 10 10 10 10 10
(一定)
正比例
(3)圆的半径与面积如下表。
半径/cm 1 2 3 4 5
面积/cm2 π 4π 9π 16π 25π
=圆周率×半径
(变量)
不成比例
圆周率×半径 π 2π 3π 4π 5π
(1)从甲地到乙地的路程是240 km,汽车行驶的速度与时间如下表。
速度/(千米/时) 40 50 60 80 100
时间/时 6 4.8 4 3 2.4
(2)圆锥的高是30cm,它的体积与底面积如下表。
底面积/cm2 5 8 10 16 20
体积/cm3 50 80 100 160 200
反比例
正比例
说一说:正比例和反比例有什么联系与区别呢?
正比例 反比例
正比例和反比例的异同点
都有两种相关联的量,一种量变化,另一种量也随着变化。
两种量“变化方向”相同
两种量“变化方向”相反
相同点
不同点
相对应的两个量的比值(商)一定
相对应的两个量的乘积一定
x
y
= k
(一定)
关系式:
关系式:
xy=k(一定)
正比例关系图象是一条射线
反比例关系图象是一条曲线
知识点
这是判断两个量是否成正比例或反比例关系的关键。
正比例和反比例
正比例
反比例
两种相关联的量的比值一定。
两种相关联的量的乘积一定。
利用比例的知识可以解决生活中哪些实际问题呢?
知识点
比例的应用
比例尺
图形的放大与缩小
用比例解决问题
放大比例尺
01
比例尺
1. 一幅地图中某两地的图上距离5cm表示实际距离15km,这幅图的比例尺是( )。
1∶300000
图上距离:实际距离=比例尺
图上距离:实际距离
=5cm∶15km
=5cm∶1500000cm
5cm与15km的长度单位不同,先统一单位。
一幅图的图上距离和实际距离的比,叫作这幅图的比例尺。
=1∶300000
1∶300000
1
300000
数值比例尺
或
线段比例尺
2∶1
缩小比例尺
3km
2. 5号线是郑州市地铁线网规划中唯一的环线地铁,全长大约40.4 km。在比例尺为 1∶20000 的37寸LED动态地图上,5号线长多少厘米?
解:设5号线的图上距离是 x cm。
解比例
40.4 km = 4040000 cm
4040000
x
=
1
20000
x=202
4040000×
1
20000
=202(cm)
答:5号线长 202 cm。
辨析练习
3.小华和小强分别将学校的花坛画了下来,如下图。如果小华是按1∶a的比例尺画的,那么小强是按( )的比例尺画的。
辨析练习
A. 1∶ a B. 1∶2a C. 1∶a D. 1∶ a
B
02
图形的放大与缩小
1. 把一个长5cm、宽3cm的长方形按3∶1放大,得到的图形的面积是( )cm 。
135
长5cm
宽3cm
放大后长15cm
放大后宽9cm
15 × 9 =135(cm )
5 × 3 = 15(cm )
×3
×3
×3
2. 把一个长15cm、宽9cm的长方形按1∶3缩小,得到的图形的面积是( )cm 。
15
长15cm
宽9cm
缩小后长5cm
缩小后宽3cm
15 × 9 =135(cm )
5 × 3 = 15(cm )
÷3
÷3
÷3
辨析练习
2. 把一个长15cm、宽9cm的长方形按1∶3缩小,得到的图形的面积是( )cm 。
15
长15cm
宽9cm
缩小后长5cm
缩小后宽3cm
图形的大小变了,但形状不变。
一个图形放大到原来的n倍或缩小到原来的 (n不为0),它的面积就放大到原来的n 倍或缩小到原来的 。
n
1
n
1
辨析练习
2. 把一个长15cm、宽9cm的长方形按1∶3缩小,得到的图形的面积是( )cm 。
15
长15cm
宽9cm
缩小后长5cm
缩小后宽3cm
画图方法:
一厘,厘清要求。
二算,计算边长。
三画,画出图形。
图形的大小变了,但形状不变。
辨析练习
图形放大
图形缩小
3 : 1
1 : 3
放大或缩小
的图形
原来图形
放大比例尺
一幅零件图纸的
比例尺是2:1
缩小比例尺
这幅地图的比例尺是1:300000
图上距离
实际距离
∶
∶
说一说:图形放大与缩小和比例尺有什么联系与区别呢?
比例尺
图形的放大与缩小
1. 李叔叔开车从甲地到乙地,前2小时行驶了100km。照这样的速度,从甲地到乙地一共要用3小时,甲乙两地相距多远?
03
用比例解决问题
2. 李叔叔开车从甲地到乙地一共用了3小时,每小时行驶50km。原路返回时每小时行驶60km,返回时用了多长时间?
解:设甲乙两地相距 x km。
3
x
=
100
2
x=150
解:设返回时用了x小时。
60x=3×50
x=2.5
答:甲乙两地相距150km。
答:返回时用了2.5小时。
辨析练习
1. 李叔叔开车从甲地到乙地,前2小时行驶了100km。照这样的速度,从甲地到乙地一共要用3小时,甲乙两地相距多远?
2. 李叔叔开车从甲地到乙地一共用了3小时,每小时行驶50km。原路返回时每小时行驶60km,返回时用了多长时间?
1. 李叔叔开车从甲地到乙地,前2小时行驶了100km。照这样的速度,从甲地到乙地一共要用3小时,甲乙两地相距多远?
2. 李叔叔开车从甲地到乙地一共用了3小时,每小时行驶50km。原路返回时每小时行驶60km,返回时用了多长时间?
01
找到题目中的不变量
辨析练习
路程÷时间=速度(一定)
速度×时间=路程(一定)
02
看哪两种量成比例关系
03
根据比例关系写出关系式
04
解方程并检验作答
正比例
反比例
知识点
比例的应用
比例尺
图形的放大与缩小
用比例解决问题
厘清相关联量之间的关系,灵活运用多种知识,才能不断提高解决问题的能力。
比例尺是一个比。
图上距离∶实际距离=比例尺
图形放大或缩小后,
形状相同,大小不同。
要正确判断相关联的两个量成什么比例关系。
比例
知识框架
综合运用
1.下面各题中的两种量之间是否有比例关系?如果有,成什么比例关系 ?
(1)比例尺一定,两地的实际距离和图上距离。
(2)积(0除外)一定,一个因数和另一个因数。
(3)梯形的上底和下底不变,梯形的面积和高。
(4)如果y=5x,y和x。
图上距离∶实际距离=比例尺(一定)
一个因数×另一个因数=积(一定)
梯形的面积÷高=(上底+下底)÷2(一定)
y÷x=5
正比例
反比例
正比例
正比例
2. 在一副比例尺是 1∶2000000 的地图上,量得甲、乙
两个城市之间的距离是 5.5 cm。在另一幅比例尺
是 1∶5000000 的地图上,这两个城市之间的图上
距离是多少?
解:设甲、乙两个城市之间的实际距离是 x cm。
x
2000000
1
=
5.5
x=11000000
解:设甲、乙两个城市之间的实际距离是 x cm。
x
5000000
1
=
11000000
x=2.2cm
答:这两个城市之间的图上距离是2.2cm。
2. 在一幅比例尺是 1∶2000000 的地图上,量得甲、乙
两个城市之间的距离是 5.5 cm。在另一幅比例尺
是 1∶5000000 的地图上,这两个城市之间的图上
距离是多少?
5
5.5×
2
=2.2(cm)
答:这两个城市之间的图上距离是 2.2 cm。
5000000
1
÷
5
2000000
1
=
2
3*. 一个服装店的所有服装都按同样的折扣销售。
(1)李阿姨买了一件上衣,原价250元,现价150元。李阿姨还想买一条裤子,原价180元,现价多少钱?
(2)张叔叔带的钱,如果买现价90元一件的衬衫,正好可以买4件。如果买原价200元一件的夹克衫,能买多少件?
(3)如果用x表示原价,y表示现价,y和x的关系式为________。
现价÷原价=折扣(一定)
正比例
(1)李阿姨买了一件上衣,原价250元,现价150元。李阿姨还想买一条裤子,原价180元,现价多少钱?
解:设现价x元。
180
250
150
=
x
250x=150×180
x=108
答:现价108元。
现价÷原价=折扣(一定)
正比例
3*. 一个服装店的所有服装都按同样的折扣销售。
(2)张叔叔带钱,如果买现价90元一件的衬衫,正好可以买4件。如果买原价200元一件的夹克衫,能买多少件?
单价×数量=总价(一定)
反比例
解:设能买x件。
90×4=200×
250
150
×x
120x=360
x=3
答:能买3件。
现在单价多少钱?
3*. 一个服装店的所有服装都按同样的折扣销售。
(1)李阿姨买了一件上衣,原价250元,现价150元。李阿姨还想买一条裤子,原价180元,现价多少钱?
(2)张叔叔带的钱,如果买现价90元一件的衬衫,正好可以买4件。如果买原价200元一件的夹克衫,能买多少件?
(3)如果用x表示原价,y表示现价,y和x的关系式为________。
y=60%x
现价÷原价=折扣(一定)
折扣=现价÷原价=150÷250=0.6
y ÷ x = ?
或y=0.6x
3*. 一个服装店的所有服装都按同样的折扣销售。
解决问题的方法
算术方法
方程
比例
我们解决生活中实际问题的策略和方法越发多样化了。厘清关系,灵活运用,才能不断提高解决问题的能力。
课后作业
完成本课时的相关习题。
谢 谢!
