第三章 位置与坐标 章末复习 课件(共21张PPT)
文档属性
| 名称 | 第三章 位置与坐标 章末复习 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-11 22:35:09 | ||
图片预览







文档简介
(共21张PPT)
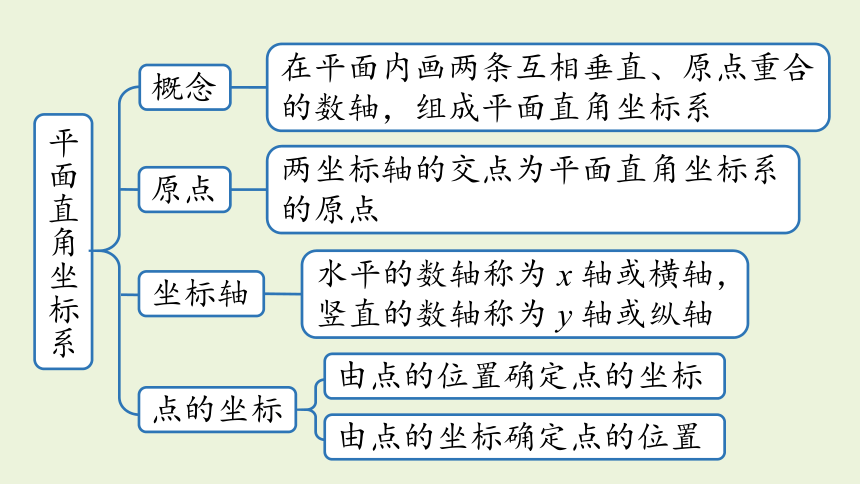
3 章末复的数轴称为 x 轴或横轴,
竖直的数轴称为 y 轴或纵轴
在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系
两坐标轴的交点为平面直角坐标系的原点
平面直角坐标系
概念
原点
坐标轴
点的坐标
由点的坐标确定点的位置
由点的位置确定点的坐标
“平行于两轴的直线上的点”的坐标特征:
(1) 平行于x轴的直线上的点:纵坐标相同;
(2)平行于y轴的直线上的点:横坐标相同.
“两坐标轴上的点”的坐标特征:
(1)x轴上的点的坐标:纵坐标为0.
(2)y轴上的点的坐标:横坐标为0.
“四个象限内的点”的坐标特征:
利用平面直角坐标系表示
建立坐标系,选择一个适当的参照点为原点,确定 x 轴、y 轴的正方向
根据具体问题确定适当的比例尺,在坐标轴上标出单位长度
在坐标平面内画出这些点,写出各点的坐标和各个地点的名称
轴对称与坐标变换
1.关于x轴对称的两个点的坐标,横坐标相同,纵坐标互为相反数;
2.关于y轴对称的两个点的坐标,横坐标互为相反数,纵坐标相同.
1.横坐标保持不变,纵坐标互为相反数,所得图形与原图形关于 x轴成轴对称.
2.纵坐标保持不变,横坐标互为相反数,所得图形与原图形关于 y轴成轴对称.
1.(邵阳中考)已知 ab>0,ab>0,则在如图所示的平面直角坐标系中,小手盖住的点的坐标可能是( )
A. (a,b) B. (a,b)
C. (a,b) D. (a,b)
B
ab>0,ab>0
a>0, b>0
a<0, b>0
随堂练习
2. 若点 A ( 2,n+3)在 x 轴上,则点 B (n1,n+1) 在( )
A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限
C
n+3=0
n1<0
n+1<0
n3
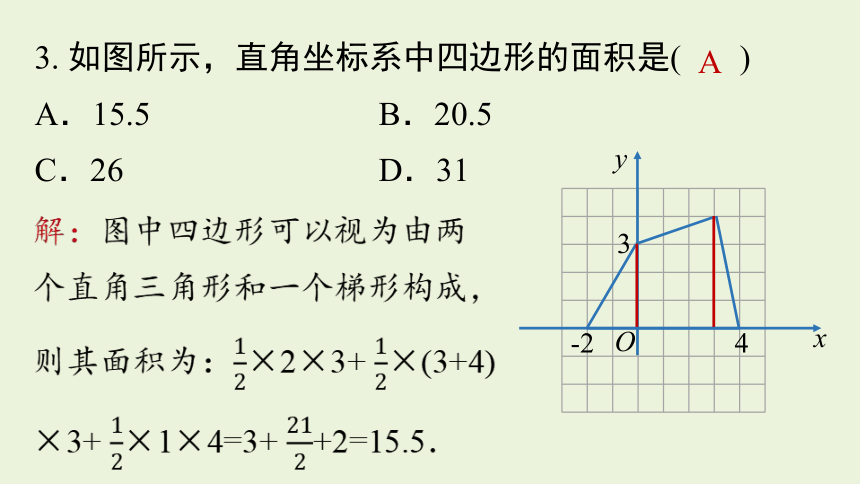
3. 如图所示,直角坐标系中四边形的面积是( )
A.15.5 B.20.5
C.26 D.31
解:图中四边形可以视为由两
个直角三角形和一个梯形构成,
则其面积为:×2×3+ ×(3+4)
×3+ ×1×4=3+ +2=15.5.
A
O
x
y
-2
3
4
4. 如图,点 A1(1,1)向上平移 1 个单位,再向右平移 2 个单位,得到点 A2;点 A2 向上平移 2 个单位,再向右平移 4 个单位,得到点 A3;点 A3 向上平移 4 个单位,再向右平移 8 个单位,得到点 A4,…,按这个规律平移得到点 A2020,则点 A2020 的横坐标为 ( )
A. 22019
B. 220201
C. 22020
D. 220201
O
y
x
A1
A2
A3
A4
解:点 A1 的横坐标为 1=211,
点 A2 的横坐为标 3=221,
点 A3 的横坐标为 7=231,
点 A4 的横坐标为 15=241,
…
按这个规律平移得到点 An 的横坐标为 2n1,
∴ 点 A2020 的横坐标为 220201.故选 B.
O
y
x
A1
A2
A3
A4
5.(广安中考)如图,在平面直角坐标系中,边长为 2 的正方形 OA1B1C1 的两边在坐标轴上,以它的对角线 OB1 为边作正方形 OB1B2C2,再以正方形 OB1B2C2的对角线 OB2 为边作正方形 OB2B3C3…
以此类推,则正方形 OB2020B2021C2021
的顶点 B2021 的坐标是_____.
解:观察,发现:B1(2,2),B2(0,4),B3(4,4),B4(8,0),B5(8,8),B6(0,16),
B7(16,16),B8(32,0),B9(32,32),…,
∴ B8n+1(24n+1,24n+1)( n 为自然数).
∵ 2021=8×252+5,
∴ B2021 的纵横坐标符号与点 B5 的相同,
∴点 B2021 的坐标为(21011,21011).
故答案为 (21011,21011).
6. 已知点 A (3+a,2a+9) 在第二象限,且到 x 轴的距离为 5,则点 a 的值是 .
2
2a+9=5
a=2
7. 点 P (a1,a29) 在 x 轴负半轴上,则点 P 的坐标是 .
(4,0)
a1<0,a29=0
a=3
8. 已知点A(x1,-5),B(2,y2).
(1)如果点A,B关于x轴对称,那么x1=_________,y2=__________;
(2)如果点A,B关于y轴对称,那么x1=_________,y2=__________.
2
5
-2
-5
9. 已知 A (4,0),点 B 在 x 轴上,且 AB=5.
(1) 若点 C 在 y 轴上,且 S三角形ABC =10,求点 C 的坐标;
解:∵ S三角形ABC=10,且 AB=5,
∴ AB 边上的高为 4.
∵ AB 在 x 轴上,点 C 在 y 轴上,
∴ 点 C 到 x 轴的距离是 4,
∴ 点 C 的坐标为 (0,4) 或 (0,4).
(2) 若 D (a3,a+2),且 S三角形ABD =15,求点 D 的坐标.
解:∵ S三角形ABD=15,且 AB=5,
∴ AB 边上的高为 6.
∵ AB 在 x 轴上,
∴ 点 D 到 x 轴的距离是 6,
∴ 点 D 的纵坐标为 6 或 6.
当 a+2=6 时,a=4,点 D 的坐标为(1,6);
当 a+2=6 时,a=8,点 D 的坐标为(11,6).
10. 如图,四边形 ABCD 顶点的坐标分别为 A (2,5),
B (5,3), C (2,4), D (4,1), 求四边形 ABCD 的面积.
解:如图,连接AC,
∵ 点 A 与点 C 的横坐标相同,
∴ AC//y 轴.
过点 B 作 BE⊥AC 于点 E,
过点 D 作DF⊥AC 于点 F,
则 BE=2(5) =3,DF=4(2) =6.
E
F
∵ A (2,5),C (2,4),∴ AC=5(4) =9.
∴ S四边形ABCD = S三角形ACB + S三角形ACD
= .
我采用分割法解这道题.
我还可以用补形法解此题.
E
F
解:如图,分别过点 A、C 作 x 轴的平行线 EH、GF,分别过点 B、D 作 y 轴的平行线 EF、GH. EH 分别与 EF、GH 交于点 E、H,GF 分别与 EF、GH 交于点 F、G.
∴EH=GH=GF=EF=9,HA=DH=GC=6,
EA=DG=FC=3,BE=8,BF=1.
E
H
F
G
∴ S四边形ABCD
= S正方形EHGFS三角形ABES三角形ADH
S三角形CGDS三角形CBF
=
.
E
H
F
G
3 章末复的数轴称为 x 轴或横轴,
竖直的数轴称为 y 轴或纵轴
在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系
两坐标轴的交点为平面直角坐标系的原点
平面直角坐标系
概念
原点
坐标轴
点的坐标
由点的坐标确定点的位置
由点的位置确定点的坐标
“平行于两轴的直线上的点”的坐标特征:
(1) 平行于x轴的直线上的点:纵坐标相同;
(2)平行于y轴的直线上的点:横坐标相同.
“两坐标轴上的点”的坐标特征:
(1)x轴上的点的坐标:纵坐标为0.
(2)y轴上的点的坐标:横坐标为0.
“四个象限内的点”的坐标特征:
利用平面直角坐标系表示
建立坐标系,选择一个适当的参照点为原点,确定 x 轴、y 轴的正方向
根据具体问题确定适当的比例尺,在坐标轴上标出单位长度
在坐标平面内画出这些点,写出各点的坐标和各个地点的名称
轴对称与坐标变换
1.关于x轴对称的两个点的坐标,横坐标相同,纵坐标互为相反数;
2.关于y轴对称的两个点的坐标,横坐标互为相反数,纵坐标相同.
1.横坐标保持不变,纵坐标互为相反数,所得图形与原图形关于 x轴成轴对称.
2.纵坐标保持不变,横坐标互为相反数,所得图形与原图形关于 y轴成轴对称.
1.(邵阳中考)已知 ab>0,ab>0,则在如图所示的平面直角坐标系中,小手盖住的点的坐标可能是( )
A. (a,b) B. (a,b)
C. (a,b) D. (a,b)
B
ab>0,ab>0
a>0, b>0
a<0, b>0
随堂练习
2. 若点 A ( 2,n+3)在 x 轴上,则点 B (n1,n+1) 在( )
A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限
C
n+3=0
n1<0
n+1<0
n3
3. 如图所示,直角坐标系中四边形的面积是( )
A.15.5 B.20.5
C.26 D.31
解:图中四边形可以视为由两
个直角三角形和一个梯形构成,
则其面积为:×2×3+ ×(3+4)
×3+ ×1×4=3+ +2=15.5.
A
O
x
y
-2
3
4
4. 如图,点 A1(1,1)向上平移 1 个单位,再向右平移 2 个单位,得到点 A2;点 A2 向上平移 2 个单位,再向右平移 4 个单位,得到点 A3;点 A3 向上平移 4 个单位,再向右平移 8 个单位,得到点 A4,…,按这个规律平移得到点 A2020,则点 A2020 的横坐标为 ( )
A. 22019
B. 220201
C. 22020
D. 220201
O
y
x
A1
A2
A3
A4
解:点 A1 的横坐标为 1=211,
点 A2 的横坐为标 3=221,
点 A3 的横坐标为 7=231,
点 A4 的横坐标为 15=241,
…
按这个规律平移得到点 An 的横坐标为 2n1,
∴ 点 A2020 的横坐标为 220201.故选 B.
O
y
x
A1
A2
A3
A4
5.(广安中考)如图,在平面直角坐标系中,边长为 2 的正方形 OA1B1C1 的两边在坐标轴上,以它的对角线 OB1 为边作正方形 OB1B2C2,再以正方形 OB1B2C2的对角线 OB2 为边作正方形 OB2B3C3…
以此类推,则正方形 OB2020B2021C2021
的顶点 B2021 的坐标是_____.
解:观察,发现:B1(2,2),B2(0,4),B3(4,4),B4(8,0),B5(8,8),B6(0,16),
B7(16,16),B8(32,0),B9(32,32),…,
∴ B8n+1(24n+1,24n+1)( n 为自然数).
∵ 2021=8×252+5,
∴ B2021 的纵横坐标符号与点 B5 的相同,
∴点 B2021 的坐标为(21011,21011).
故答案为 (21011,21011).
6. 已知点 A (3+a,2a+9) 在第二象限,且到 x 轴的距离为 5,则点 a 的值是 .
2
2a+9=5
a=2
7. 点 P (a1,a29) 在 x 轴负半轴上,则点 P 的坐标是 .
(4,0)
a1<0,a29=0
a=3
8. 已知点A(x1,-5),B(2,y2).
(1)如果点A,B关于x轴对称,那么x1=_________,y2=__________;
(2)如果点A,B关于y轴对称,那么x1=_________,y2=__________.
2
5
-2
-5
9. 已知 A (4,0),点 B 在 x 轴上,且 AB=5.
(1) 若点 C 在 y 轴上,且 S三角形ABC =10,求点 C 的坐标;
解:∵ S三角形ABC=10,且 AB=5,
∴ AB 边上的高为 4.
∵ AB 在 x 轴上,点 C 在 y 轴上,
∴ 点 C 到 x 轴的距离是 4,
∴ 点 C 的坐标为 (0,4) 或 (0,4).
(2) 若 D (a3,a+2),且 S三角形ABD =15,求点 D 的坐标.
解:∵ S三角形ABD=15,且 AB=5,
∴ AB 边上的高为 6.
∵ AB 在 x 轴上,
∴ 点 D 到 x 轴的距离是 6,
∴ 点 D 的纵坐标为 6 或 6.
当 a+2=6 时,a=4,点 D 的坐标为(1,6);
当 a+2=6 时,a=8,点 D 的坐标为(11,6).
10. 如图,四边形 ABCD 顶点的坐标分别为 A (2,5),
B (5,3), C (2,4), D (4,1), 求四边形 ABCD 的面积.
解:如图,连接AC,
∵ 点 A 与点 C 的横坐标相同,
∴ AC//y 轴.
过点 B 作 BE⊥AC 于点 E,
过点 D 作DF⊥AC 于点 F,
则 BE=2(5) =3,DF=4(2) =6.
E
F
∵ A (2,5),C (2,4),∴ AC=5(4) =9.
∴ S四边形ABCD = S三角形ACB + S三角形ACD
= .
我采用分割法解这道题.
我还可以用补形法解此题.
E
F
解:如图,分别过点 A、C 作 x 轴的平行线 EH、GF,分别过点 B、D 作 y 轴的平行线 EF、GH. EH 分别与 EF、GH 交于点 E、H,GF 分别与 EF、GH 交于点 F、G.
∴EH=GH=GF=EF=9,HA=DH=GC=6,
EA=DG=FC=3,BE=8,BF=1.
E
H
F
G
∴ S四边形ABCD
= S正方形EHGFS三角形ABES三角形ADH
S三角形CGDS三角形CBF
=
.
E
H
F
G
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
