第四章 一次函数 章末复习 课件(共29张PPT)
文档属性
| 名称 | 第四章 一次函数 章末复习 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-11 22:36:58 | ||
图片预览



文档简介
(共29张PPT)
4. 章末复习
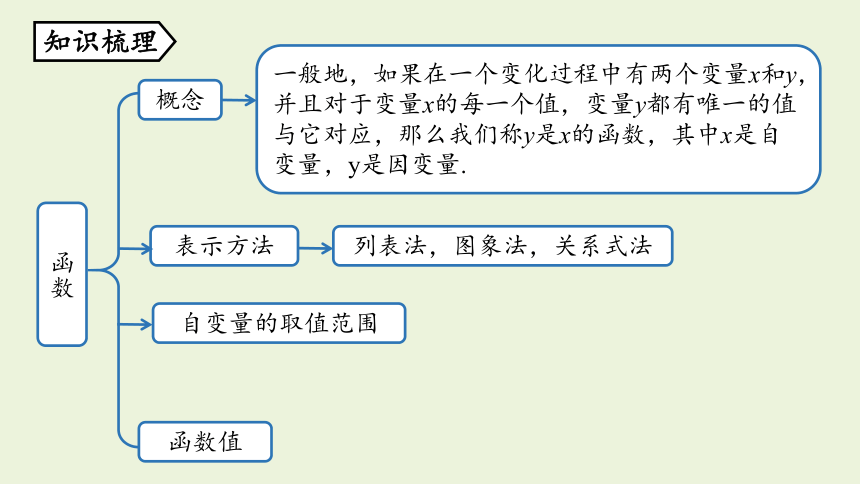
函数
概念
一般地,如果在一个变化过程中有两个变量x和y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的函数,其中x是自变量,y是因变量.
表示方法
列表法,图象法,关系式法
自变量的取值范围
函数值
知识梳理
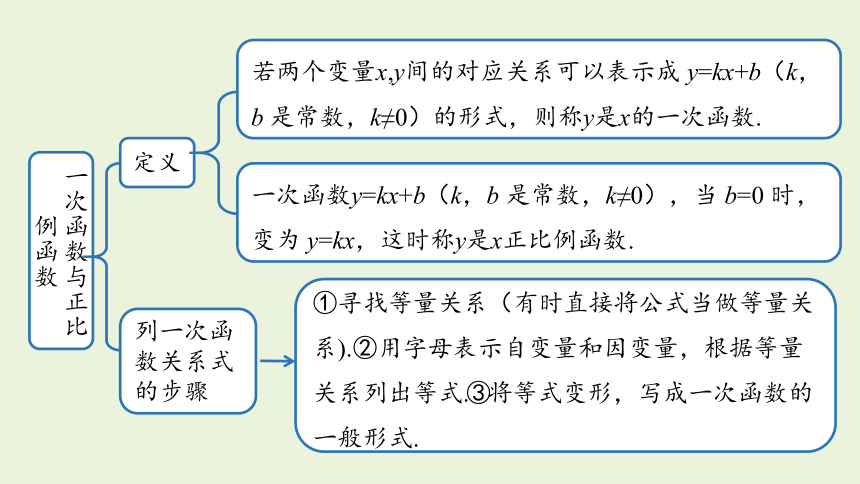
一次函数与正比例函数
定义
列一次函数关系式的步骤
若两个变量x,y间的对应关系可以表示成 y=kx+b(k,b 是常数,k≠0)的形式,则称y是x的一次函数.
①寻找等量关系(有时直接将公式当做等量关系).②用字母表示自变量和因变量,根据等量关系列出等式.③将等式变形,写成一次函数的一般形式.
一次函数y=kx+b(k,b 是常数,k≠0),当 b=0 时,变为 y=kx,这时称y是x正比例函数.
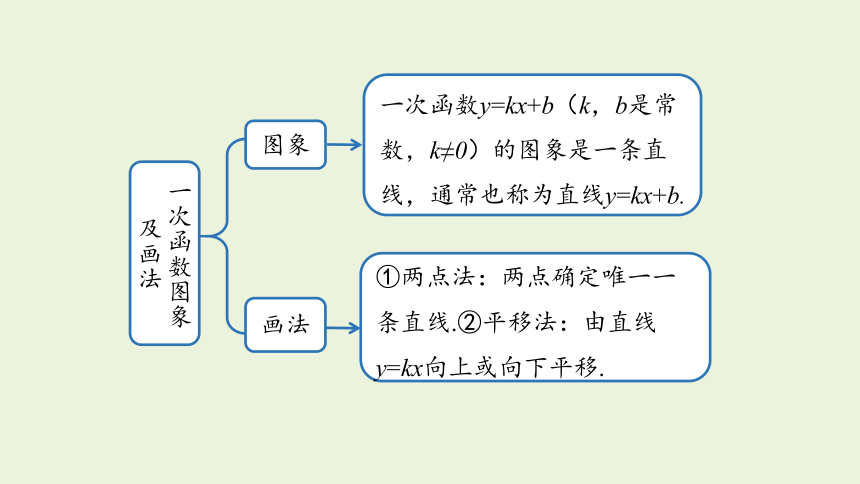
一次函数图象及画法
图象
画法
一次函数y=kx+b(k,b是常数,k≠0)的图象是一条直线,通常也称为直线y=kx+b.
①两点法:两点确定唯一一条直线.②平移法:由直线y=kx向上或向下平移.
一次函数的性质
k>0
k<0
①b>0,经过一、二、三象限,y随x的增大而增大;
②b<0,经过一、三、四象限,y随x的增大而增大;
①b>0,经过一、二、四象限,y随x的增大而减小;
②b<0,经过二、三、四象限,y随x的增大而减小;
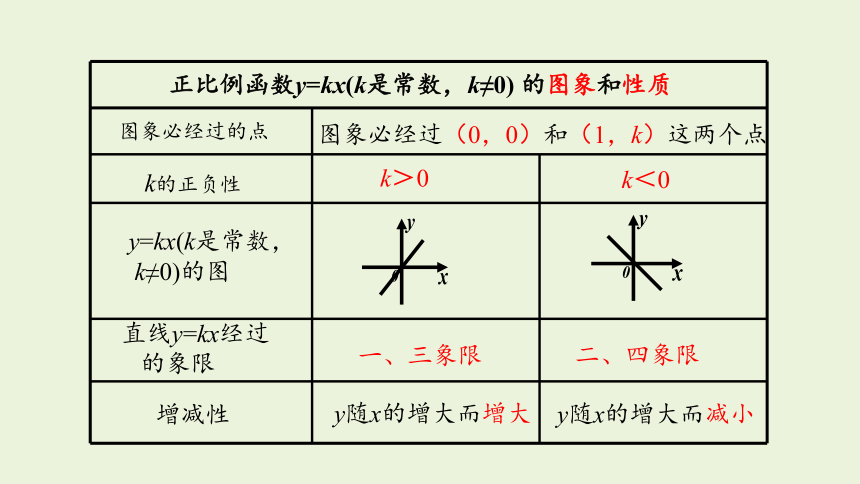
一、三象限
二、四象限
y随x的增大而减小
y随x的增大而增大
图象必经过(0,0)和(1,k)这两个点
正比例函数y=kx(k是常数,k≠0) 的图象和性质
直线y=kx经过
的象限
增减性
图象必经过的点
k的正负性
k>0
k<0
y=kx(k是常数,
k≠0)的图
x
y
0
x
y
0
求一次
函数表达式
待定系数法
①设;
②列;
③解;
④代.
步骤
关系
利用一次函数图象解一元一次方程
①从“数”上看;
②从“形”上看.
①转化;
②画图象;
③找交点.
一次函数与一元一次方程
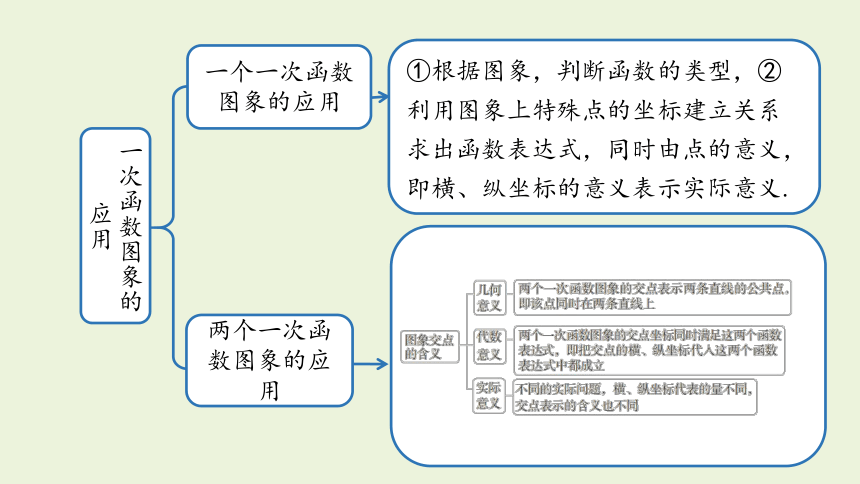
一次函数图象的应用
一个一次函数图象的应用
两个一次函数图象的应用
①根据图象,判断函数的类型,②利用图象上特殊点的坐标建立关系求出函数表达式,同时由点的意义,即横、纵坐标的意义表示实际意义.
随堂练习
1.下列变量间的关系不是函数关系的是( ).
A.圆的半径与圆的面积
B.正方形的周长与正方形的边长
C.在汽车速度一定的情况下,时间与路程
D.等腰三角形的底边长与面积
D
2.小刚从家去学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车匀速行驶一段时间后到达学校,小刚从家到学校行驶路程 s(单位:m)与时间 t(单位:min)之间的函数关系的大致图象是( ).
B
3.周日下午,小红和小兰相约在某公交车站一起乘车回学校,小红从家出发先步行到车站,等小兰到车站后两人一起乘公交车回到学校.下图表示小红离开家的路程 y(千米)和所用的时间 x(分钟)之间的函数关系.下列哪个说法是错误的( ).
A.小红从家到公交车站步行了2千米.
B.小红乘坐公交车用了30分钟.
C.小红在公交车站等小兰用了10分钟.
D.公交车的平均速度是34千米/小时.
解:从图上来看,小红出发20分钟后小红从家走到了公交车站,路程变化为2千米;20分~30分之间小红离开家的路程未发生变化,说明此阶段是
在公交车站等小兰;30分~ 60分小
红和小兰一起乘坐公交车到达学校,
用时30分钟,路程为15千米.公交车
速度为15÷0.5=30 (千米/时).
故选D.
4.下列所有表达式中,是一次函数但不是正比例函数的是( )
A.
B.
C.
D.
既不是一次函数也不是正比例函数
化简得y=2x,是正比例函数
是一次函数但不是正比例函数
是正比例函数
B
5.下列图形中,表示一次函数 y1=mx+n 与正比例函数y2=mnx(m、n为常数,且mn≠0)的图象的是( )
分析 结论
mn>0 m>0, n>0 y1图象经过第一、二、三象限; y2的图象经过第一、三象限 D错误
m<0, n<0 y1图象经过第二、三、四象限; y2的图象经过第一、三象限 B错误
mn<0 m>0,n<0 y1图象经过第一、三、四象限; y2的图象经过第二、四象限 C错误
m<0,n>0 y1图象经过第一、二、四象限; y2的图象经过第二、四象限 A正确
6.一元一次方程 ax-b=0 的解为 x=5,则函数 y=ax-b 与 x 轴的交点坐标是( ).
A.(0,5) B.(0 ,-5)
C
C.(5,0) D.(-5 ,0)
解析:ax-b=0 的解就是当函数 y=ax-b 中 y=0 时 x 的值.
7.如图,一次函数y=2x+1的图象与坐标轴分别交于A,B两点,O为坐标原点,则△AOB的面积是( ).
A. B. C. 2 D.4
解析:依据题意可知,当x=0时,y=1; y=0时,x=-. 所以A(-,0),
B(0,1),则有OA=,OB=1. 则△AOB的面积是.
A
8.已知函数 y=2x+3.
(1)试判断点 A(1,5)和点 B(-1,3)是否在此 函数图象上;
(2)已知点 C(m,m+3)在此函数图象上,求 m 的值.
当 x=1 时,y=21+3=5
当 x=-1 时,y=2(-1)+3=1≠3
2m+3=m+3,解得m=0
将 x=m, y=m+3 代入函数解析式中
点 B不在图像上
点 A在图像上
9.小李从西安通过某快递公司给在南昌的外婆邮寄一盒樱桃,快递时,他了解到这个公司除收取每次 6 元的包装费外,樱桃不超过 1kg 收费 22 元,超过 1kg 的部分按照每千克 10 元加收费用.设该公司从西安到南昌快递樱桃的费用为 y(元),所寄樱桃为 x(kg).
(1)求 y 与 x 之间的函数解析式;
(2)已知小李给外婆快递了 2.5kg 樱桃,请你求出这次快递的费用是多少元?
解:(1)由题意得,当 0当 x>1 时,y=28+10(x-1)=10x+18;
28 ( 010x+18 ( x>1 ).
所以 y 与 x 之间的函数解析式为 y =
28 ( 010x+18 ( x>1 ),
(2)因为 y=
当 x=2.5>1 时,y=102.5+18=43;
所以小李此次的快寄费用是 43 元.
10.根据记录,从地面向上 11 km 以内,每升高 1km,气温降低6℃;又知道在距离地面 11km 以上的高空,气温几乎不变.若地面气温为 m(℃),设距地面的高度为 x(km) 处的气温为 y(℃).
(1)写出距地面的高度在 11 km 以内的 y 与 x 之间的函数解析式;
解:由题意知,y=m-6x(0≤x≤11).
(2)上周日,小敏乘飞机从上海飞回西安途中,某一时刻,她从机舱内屏幕显示的相关数据得知,飞机外
气温为-26℃时,飞机距地面的高度为 7 km,求当时这架飞机下方地面的气温;小敏想,假如飞机当时在距地面 12 km 的高空,飞机外的气温是多少度呢?请求出假如当飞机距地面 12 km 时,飞机外的气温.
解:将 x=7, y=-26 代入 y=m-6x,得 -26=m-42,解得m=16,
即当飞机外气温为-26 ℃时,飞机下方地面温度为16 ℃.
因为 12>11,所以此时飞机外的气温为16-6×11=50 (℃).
(2)将 x=7 时,y=-26 代入 y=m-6x,得 -26=m-42,
解得:m=16.
所以当时这架飞机下方地面的气温为 16℃.
因为 12>11,所以 y=-50℃,则假如当飞机距地面12km 时,飞机外的气温为 -50℃.
11.在“美丽家乡,清洁乡村”活动中,李家村村长提出两种购买垃圾桶的方案,方案一:买分类垃圾桶,需要费用 3000 元,以后每月的垃圾处理费用为 250 元;方案二:买不分类垃圾桶,需要费用 1000 元,以后每月的垃圾处理费用为 500 元.设方案一的购买费和垃圾处理费共 y1 元,方案二的购买费和垃圾处理费共 y2 元,交费时间为 x 个月.
(2)在同一平面直角坐标系中,画出函数 y2,y2 的图象;
(3)在垃圾桶使用寿命相同的情况下,哪种方案更省钱?
解:(1) 由题意可得:y1=250x+3000(x≥0);y2=500x+1000(x≥0).
(1)直接写出 y1,y2 与 x 的函数解析式;
(2)对于 y1=250x+3000(x≥0),当 x=0 时,y1=3000;当 x=4 时,y1=4000 . 过点(0,3000),(4,4000)在第一象限内画射线,即是函数 y1=250x+3000(x≥0)的图象.
对于 y2=500x+1000(x≥0) ,当 x=0 时,y2=1000;
当 x=4 时,y1=3000 . 过点(0,1000),(4,3000)在第一象限内画射线,即是函数 y2=500x+1000(x≥0)的图象.
y1=250x+3000(x≥0),过点(0,3000),(4,4000); y2=500x+1000(x≥0),过点(0,1000),(4,3000).
解得 x=8,
y=5000.
(3)解方程组 y=250x+3000,
y=500x+1000,
所以函数 y1=250x+3000(x≥0),y2=500x+1000(x≥0)
的图象的交点坐标为(8,5000).观察图象可得:
当x>8时,y1当x=8时,y1=y2,两种方案费用一样;
当0≤x<8时,y1>y2,方案二更省钱.
4. 章末复习
函数
概念
一般地,如果在一个变化过程中有两个变量x和y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的函数,其中x是自变量,y是因变量.
表示方法
列表法,图象法,关系式法
自变量的取值范围
函数值
知识梳理
一次函数与正比例函数
定义
列一次函数关系式的步骤
若两个变量x,y间的对应关系可以表示成 y=kx+b(k,b 是常数,k≠0)的形式,则称y是x的一次函数.
①寻找等量关系(有时直接将公式当做等量关系).②用字母表示自变量和因变量,根据等量关系列出等式.③将等式变形,写成一次函数的一般形式.
一次函数y=kx+b(k,b 是常数,k≠0),当 b=0 时,变为 y=kx,这时称y是x正比例函数.
一次函数图象及画法
图象
画法
一次函数y=kx+b(k,b是常数,k≠0)的图象是一条直线,通常也称为直线y=kx+b.
①两点法:两点确定唯一一条直线.②平移法:由直线y=kx向上或向下平移.
一次函数的性质
k>0
k<0
①b>0,经过一、二、三象限,y随x的增大而增大;
②b<0,经过一、三、四象限,y随x的增大而增大;
①b>0,经过一、二、四象限,y随x的增大而减小;
②b<0,经过二、三、四象限,y随x的增大而减小;
一、三象限
二、四象限
y随x的增大而减小
y随x的增大而增大
图象必经过(0,0)和(1,k)这两个点
正比例函数y=kx(k是常数,k≠0) 的图象和性质
直线y=kx经过
的象限
增减性
图象必经过的点
k的正负性
k>0
k<0
y=kx(k是常数,
k≠0)的图
x
y
0
x
y
0
求一次
函数表达式
待定系数法
①设;
②列;
③解;
④代.
步骤
关系
利用一次函数图象解一元一次方程
①从“数”上看;
②从“形”上看.
①转化;
②画图象;
③找交点.
一次函数与一元一次方程
一次函数图象的应用
一个一次函数图象的应用
两个一次函数图象的应用
①根据图象,判断函数的类型,②利用图象上特殊点的坐标建立关系求出函数表达式,同时由点的意义,即横、纵坐标的意义表示实际意义.
随堂练习
1.下列变量间的关系不是函数关系的是( ).
A.圆的半径与圆的面积
B.正方形的周长与正方形的边长
C.在汽车速度一定的情况下,时间与路程
D.等腰三角形的底边长与面积
D
2.小刚从家去学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车匀速行驶一段时间后到达学校,小刚从家到学校行驶路程 s(单位:m)与时间 t(单位:min)之间的函数关系的大致图象是( ).
B
3.周日下午,小红和小兰相约在某公交车站一起乘车回学校,小红从家出发先步行到车站,等小兰到车站后两人一起乘公交车回到学校.下图表示小红离开家的路程 y(千米)和所用的时间 x(分钟)之间的函数关系.下列哪个说法是错误的( ).
A.小红从家到公交车站步行了2千米.
B.小红乘坐公交车用了30分钟.
C.小红在公交车站等小兰用了10分钟.
D.公交车的平均速度是34千米/小时.
解:从图上来看,小红出发20分钟后小红从家走到了公交车站,路程变化为2千米;20分~30分之间小红离开家的路程未发生变化,说明此阶段是
在公交车站等小兰;30分~ 60分小
红和小兰一起乘坐公交车到达学校,
用时30分钟,路程为15千米.公交车
速度为15÷0.5=30 (千米/时).
故选D.
4.下列所有表达式中,是一次函数但不是正比例函数的是( )
A.
B.
C.
D.
既不是一次函数也不是正比例函数
化简得y=2x,是正比例函数
是一次函数但不是正比例函数
是正比例函数
B
5.下列图形中,表示一次函数 y1=mx+n 与正比例函数y2=mnx(m、n为常数,且mn≠0)的图象的是( )
分析 结论
mn>0 m>0, n>0 y1图象经过第一、二、三象限; y2的图象经过第一、三象限 D错误
m<0, n<0 y1图象经过第二、三、四象限; y2的图象经过第一、三象限 B错误
mn<0 m>0,n<0 y1图象经过第一、三、四象限; y2的图象经过第二、四象限 C错误
m<0,n>0 y1图象经过第一、二、四象限; y2的图象经过第二、四象限 A正确
6.一元一次方程 ax-b=0 的解为 x=5,则函数 y=ax-b 与 x 轴的交点坐标是( ).
A.(0,5) B.(0 ,-5)
C
C.(5,0) D.(-5 ,0)
解析:ax-b=0 的解就是当函数 y=ax-b 中 y=0 时 x 的值.
7.如图,一次函数y=2x+1的图象与坐标轴分别交于A,B两点,O为坐标原点,则△AOB的面积是( ).
A. B. C. 2 D.4
解析:依据题意可知,当x=0时,y=1; y=0时,x=-. 所以A(-,0),
B(0,1),则有OA=,OB=1. 则△AOB的面积是.
A
8.已知函数 y=2x+3.
(1)试判断点 A(1,5)和点 B(-1,3)是否在此 函数图象上;
(2)已知点 C(m,m+3)在此函数图象上,求 m 的值.
当 x=1 时,y=21+3=5
当 x=-1 时,y=2(-1)+3=1≠3
2m+3=m+3,解得m=0
将 x=m, y=m+3 代入函数解析式中
点 B不在图像上
点 A在图像上
9.小李从西安通过某快递公司给在南昌的外婆邮寄一盒樱桃,快递时,他了解到这个公司除收取每次 6 元的包装费外,樱桃不超过 1kg 收费 22 元,超过 1kg 的部分按照每千克 10 元加收费用.设该公司从西安到南昌快递樱桃的费用为 y(元),所寄樱桃为 x(kg).
(1)求 y 与 x 之间的函数解析式;
(2)已知小李给外婆快递了 2.5kg 樱桃,请你求出这次快递的费用是多少元?
解:(1)由题意得,当 0
28 ( 0
所以 y 与 x 之间的函数解析式为 y =
28 ( 0
(2)因为 y=
当 x=2.5>1 时,y=102.5+18=43;
所以小李此次的快寄费用是 43 元.
10.根据记录,从地面向上 11 km 以内,每升高 1km,气温降低6℃;又知道在距离地面 11km 以上的高空,气温几乎不变.若地面气温为 m(℃),设距地面的高度为 x(km) 处的气温为 y(℃).
(1)写出距地面的高度在 11 km 以内的 y 与 x 之间的函数解析式;
解:由题意知,y=m-6x(0≤x≤11).
(2)上周日,小敏乘飞机从上海飞回西安途中,某一时刻,她从机舱内屏幕显示的相关数据得知,飞机外
气温为-26℃时,飞机距地面的高度为 7 km,求当时这架飞机下方地面的气温;小敏想,假如飞机当时在距地面 12 km 的高空,飞机外的气温是多少度呢?请求出假如当飞机距地面 12 km 时,飞机外的气温.
解:将 x=7, y=-26 代入 y=m-6x,得 -26=m-42,解得m=16,
即当飞机外气温为-26 ℃时,飞机下方地面温度为16 ℃.
因为 12>11,所以此时飞机外的气温为16-6×11=50 (℃).
(2)将 x=7 时,y=-26 代入 y=m-6x,得 -26=m-42,
解得:m=16.
所以当时这架飞机下方地面的气温为 16℃.
因为 12>11,所以 y=-50℃,则假如当飞机距地面12km 时,飞机外的气温为 -50℃.
11.在“美丽家乡,清洁乡村”活动中,李家村村长提出两种购买垃圾桶的方案,方案一:买分类垃圾桶,需要费用 3000 元,以后每月的垃圾处理费用为 250 元;方案二:买不分类垃圾桶,需要费用 1000 元,以后每月的垃圾处理费用为 500 元.设方案一的购买费和垃圾处理费共 y1 元,方案二的购买费和垃圾处理费共 y2 元,交费时间为 x 个月.
(2)在同一平面直角坐标系中,画出函数 y2,y2 的图象;
(3)在垃圾桶使用寿命相同的情况下,哪种方案更省钱?
解:(1) 由题意可得:y1=250x+3000(x≥0);y2=500x+1000(x≥0).
(1)直接写出 y1,y2 与 x 的函数解析式;
(2)对于 y1=250x+3000(x≥0),当 x=0 时,y1=3000;当 x=4 时,y1=4000 . 过点(0,3000),(4,4000)在第一象限内画射线,即是函数 y1=250x+3000(x≥0)的图象.
对于 y2=500x+1000(x≥0) ,当 x=0 时,y2=1000;
当 x=4 时,y1=3000 . 过点(0,1000),(4,3000)在第一象限内画射线,即是函数 y2=500x+1000(x≥0)的图象.
y1=250x+3000(x≥0),过点(0,3000),(4,4000); y2=500x+1000(x≥0),过点(0,1000),(4,3000).
解得 x=8,
y=5000.
(3)解方程组 y=250x+3000,
y=500x+1000,
所以函数 y1=250x+3000(x≥0),y2=500x+1000(x≥0)
的图象的交点坐标为(8,5000).观察图象可得:
当x>8时,y1
当0≤x<8时,y1>y2,方案二更省钱.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
