第六章 数据的分析 章末复习 课件(共20张PPT)
文档属性
| 名称 | 第六章 数据的分析 章末复习 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-11 22:40:07 | ||
图片预览







文档简介
(共20张PPT)
6 章末复习
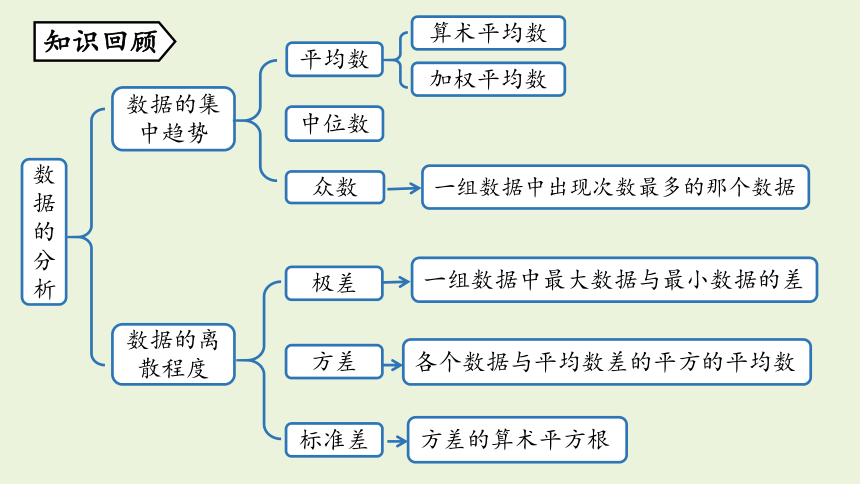
知识回顾
数据的离散程度
数据的集中趋势
算术平均数
数据的分析
平均数
中位数
一组数据中最大数据与最小数据的差
各个数据与平均数差的平方的平均数
标准差
众数
加权平均数
一组数据中出现次数最多的那个数据
方差
极差
方差的算术平方根
1. 求加权平均数
算术平均数是加权平均数的特例. 加权平均数的实质就是考虑不同权重的平均数,当加权平均数的各项权相等时,就变成了算术平均数.
2.求中位数
将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则称处于中间位置的数为这组数据的中位数;如果数据的个数是偶数,则称中间两个数据的平均数为这组数据的中位数.
3. 求方差
在平均数相差不多的情况下,方差是衡量一组数据波动大小的量,方差越小,数据的波动就越小,证明数据越均数.
课堂练习
1. 一组6个数 1,2,3,x, y,z 的平均数是 4.
(1)求 x,y, z 三数的平均数;
(2)求 4x+5,4y+6,4z+7 的平均数.
解:(1)由上题知 1+2+3+x+y+z=24,∴x+y+z=18,
∴x,y,z三数的平均数是6.
(2)∵( 4x+5)+(4y+6)+(4z+7)=4(x+y+z)+18=4×18+18=90,
∴(4x+5+4y+6+4z+7)÷3=90÷3=30.
2.已知数据 x1 ,x2 ,x3 ,x4 ,x5 的平均数为 a,则数据 5x1 ,5x2 ,5x3 ,5x4 ,5x5 的平均数为( ).
这组数据的系数有何特点?
A. a B. 5a C. D. 10a
B
所以 5x1 ,5x2 ,5x3 ,5x4 ,5x5 的平均数为
= = 5a.
解析:因为x1 ,x2,x3,x4,x5 的平均数为 a,
所以 x1+x2+x3+x4+x5=5a.
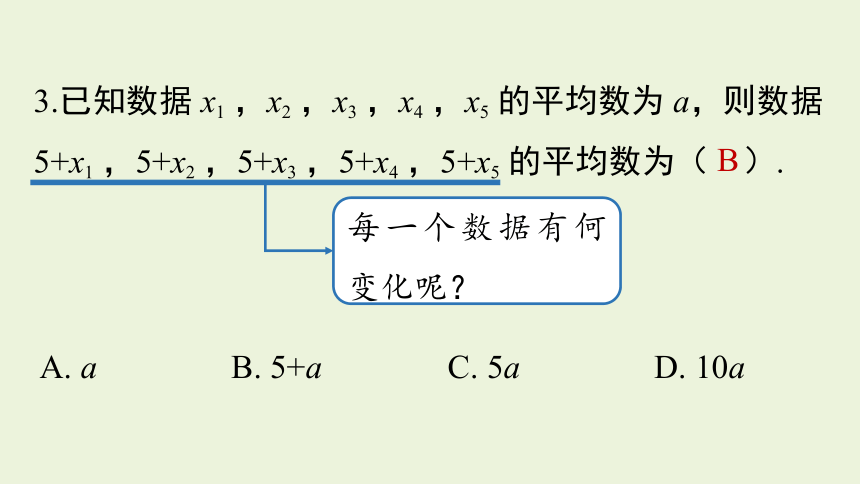
3.已知数据 x1 ,x2 ,x3 ,x4 ,x5 的平均数为 a,则数据5+x1 ,5+x2 ,5+x3 ,5+x4 ,5+x5 的平均数为( ).
每一个数据有何变化呢?
B
A. a B. 5+a C. 5a D. 10a
解析:因为x1 ,x2 ,x3 ,x4 ,x5的平均数为a,
所以x1+x2+x3+x4+x5=5a.
所以 5+x1 ,5+x2 ,5+x3 ,5+x4 ,5+x5的平均数为
==5+a.
4.已知数据 x1 ,x2 ,x3 ,x4 ,x5 的平均数为 a,则数据5+5x1 ,5+5x2 ,5+5x3 ,5+5x4 ,5+5x5 的平均数为( ).
猜想一下这组数据的平均数?
B
A. 5a B. 5+5a C. 5+a D. 10a
解析: x1 ,x2 ,x3 ,x4 ,x5 的平均数为 a,所以 x1+x2+x3+x4+x5=5a.
所以 5+5x1 ,5+5x2 ,5+5x3 ,5+5x4 ,5+5x5 的平均数为
= = 5+a.
平均数的性质
若一组数据 x1,x2, xn的平均数为,则有:
(1)数据nx1,nx2, nxn的平均数为n;
(2)数据x1+b,x2+b, xn+b的平均数为+b;
(3)数据nx1+b,nx2+b, nxn+b的平均数为n+b.
5.若一组数据a1 , a2 , a3的平均数是4,方差是3,则数据a1+2, a2+2 , a3+2的平均数和方差分别是( ).
A. 4,3 B. 6,3 C. 3,4 D. 6,5
解析: ∵数据a1 ,a2 ,a3的平均数是4,
∴ (a1+a2+a3)=4,
∴ (a1+2+a2+2+a3+2)= (a1+a2+a3)+2=4+2=6.
B
∵数据a1 , a2 , a3的方差是3,
∴ [+] = 3,
∴数据a1+2, a2+2,a3+2的方差为
[+]
= [+] = 3. 故选B.
6. 某班中考数学成绩如下:得100分7人,得90分14人,得80分17人,得70分8人,得60分3人,得50分1人,平均分为 ,中位数为 ,众数为 .
82.2
80
80
7. 某班团支部统计了该班甲、乙、丙、丁四名同学在5月份“书香校园”活动中的课外阅读时间,他们平均每天课外阅读时间 x 与方差 s2如下表所示,你认为表现最好的是( )
A.甲 B.乙
C.丙 D.丁
C
8. 从甲、乙两名射击运动员中选拔一名参加比赛,预赛中,他们每人各打10发子弹,命中的环数如下:
甲:9, 8, 9, 9, 8, 9.5, 10, 10, 8.5, 9;
乙:8.5, 8.5, 9.5, 9.5, 10, 8, 9, 9, 8, 10.
(1)谁的平均成绩高?
(2)谁的成绩比较稳定?
(3)你认为派 去参加比赛比较合适?请结合计算加以说明.
解:(1)甲的平均成绩:
(9+8+9+9+8+9.5+10+10+8.5+9)÷10=9
乙的平均成绩:
(8.5+8.5+9.5+9.5+10+8+9+9+8+10)÷10=9
答:甲、乙二人的平均成绩一样高.
甲:9, 8, 9, 9, 8, 9.5, 10, 10, 8.5, 9;
乙:8.5, 8.5, 9.5, 9.5, 10, 8, 9, 9, 8, 10.
(1)谁的平均成绩高?
解:(2)
甲:9, 8, 9, 9, 8, 9.5, 10, 10, 8.5, 9;
乙:8.5, 8.5, 9.5, 9.5, 10, 8, 9, 9, 8, 10.
(2)谁的成绩比较稳定?
(3)你认为派 去参加比赛比较合适?请结合计算加以说明.
∴甲的成绩比较稳定.
甲
6 章末复习
知识回顾
数据的离散程度
数据的集中趋势
算术平均数
数据的分析
平均数
中位数
一组数据中最大数据与最小数据的差
各个数据与平均数差的平方的平均数
标准差
众数
加权平均数
一组数据中出现次数最多的那个数据
方差
极差
方差的算术平方根
1. 求加权平均数
算术平均数是加权平均数的特例. 加权平均数的实质就是考虑不同权重的平均数,当加权平均数的各项权相等时,就变成了算术平均数.
2.求中位数
将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则称处于中间位置的数为这组数据的中位数;如果数据的个数是偶数,则称中间两个数据的平均数为这组数据的中位数.
3. 求方差
在平均数相差不多的情况下,方差是衡量一组数据波动大小的量,方差越小,数据的波动就越小,证明数据越均数.
课堂练习
1. 一组6个数 1,2,3,x, y,z 的平均数是 4.
(1)求 x,y, z 三数的平均数;
(2)求 4x+5,4y+6,4z+7 的平均数.
解:(1)由上题知 1+2+3+x+y+z=24,∴x+y+z=18,
∴x,y,z三数的平均数是6.
(2)∵( 4x+5)+(4y+6)+(4z+7)=4(x+y+z)+18=4×18+18=90,
∴(4x+5+4y+6+4z+7)÷3=90÷3=30.
2.已知数据 x1 ,x2 ,x3 ,x4 ,x5 的平均数为 a,则数据 5x1 ,5x2 ,5x3 ,5x4 ,5x5 的平均数为( ).
这组数据的系数有何特点?
A. a B. 5a C. D. 10a
B
所以 5x1 ,5x2 ,5x3 ,5x4 ,5x5 的平均数为
= = 5a.
解析:因为x1 ,x2,x3,x4,x5 的平均数为 a,
所以 x1+x2+x3+x4+x5=5a.
3.已知数据 x1 ,x2 ,x3 ,x4 ,x5 的平均数为 a,则数据5+x1 ,5+x2 ,5+x3 ,5+x4 ,5+x5 的平均数为( ).
每一个数据有何变化呢?
B
A. a B. 5+a C. 5a D. 10a
解析:因为x1 ,x2 ,x3 ,x4 ,x5的平均数为a,
所以x1+x2+x3+x4+x5=5a.
所以 5+x1 ,5+x2 ,5+x3 ,5+x4 ,5+x5的平均数为
==5+a.
4.已知数据 x1 ,x2 ,x3 ,x4 ,x5 的平均数为 a,则数据5+5x1 ,5+5x2 ,5+5x3 ,5+5x4 ,5+5x5 的平均数为( ).
猜想一下这组数据的平均数?
B
A. 5a B. 5+5a C. 5+a D. 10a
解析: x1 ,x2 ,x3 ,x4 ,x5 的平均数为 a,所以 x1+x2+x3+x4+x5=5a.
所以 5+5x1 ,5+5x2 ,5+5x3 ,5+5x4 ,5+5x5 的平均数为
= = 5+a.
平均数的性质
若一组数据 x1,x2, xn的平均数为,则有:
(1)数据nx1,nx2, nxn的平均数为n;
(2)数据x1+b,x2+b, xn+b的平均数为+b;
(3)数据nx1+b,nx2+b, nxn+b的平均数为n+b.
5.若一组数据a1 , a2 , a3的平均数是4,方差是3,则数据a1+2, a2+2 , a3+2的平均数和方差分别是( ).
A. 4,3 B. 6,3 C. 3,4 D. 6,5
解析: ∵数据a1 ,a2 ,a3的平均数是4,
∴ (a1+a2+a3)=4,
∴ (a1+2+a2+2+a3+2)= (a1+a2+a3)+2=4+2=6.
B
∵数据a1 , a2 , a3的方差是3,
∴ [+] = 3,
∴数据a1+2, a2+2,a3+2的方差为
[+]
= [+] = 3. 故选B.
6. 某班中考数学成绩如下:得100分7人,得90分14人,得80分17人,得70分8人,得60分3人,得50分1人,平均分为 ,中位数为 ,众数为 .
82.2
80
80
7. 某班团支部统计了该班甲、乙、丙、丁四名同学在5月份“书香校园”活动中的课外阅读时间,他们平均每天课外阅读时间 x 与方差 s2如下表所示,你认为表现最好的是( )
A.甲 B.乙
C.丙 D.丁
C
8. 从甲、乙两名射击运动员中选拔一名参加比赛,预赛中,他们每人各打10发子弹,命中的环数如下:
甲:9, 8, 9, 9, 8, 9.5, 10, 10, 8.5, 9;
乙:8.5, 8.5, 9.5, 9.5, 10, 8, 9, 9, 8, 10.
(1)谁的平均成绩高?
(2)谁的成绩比较稳定?
(3)你认为派 去参加比赛比较合适?请结合计算加以说明.
解:(1)甲的平均成绩:
(9+8+9+9+8+9.5+10+10+8.5+9)÷10=9
乙的平均成绩:
(8.5+8.5+9.5+9.5+10+8+9+9+8+10)÷10=9
答:甲、乙二人的平均成绩一样高.
甲:9, 8, 9, 9, 8, 9.5, 10, 10, 8.5, 9;
乙:8.5, 8.5, 9.5, 9.5, 10, 8, 9, 9, 8, 10.
(1)谁的平均成绩高?
解:(2)
甲:9, 8, 9, 9, 8, 9.5, 10, 10, 8.5, 9;
乙:8.5, 8.5, 9.5, 9.5, 10, 8, 9, 9, 8, 10.
(2)谁的成绩比较稳定?
(3)你认为派 去参加比赛比较合适?请结合计算加以说明.
∴甲的成绩比较稳定.
甲
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
