人教版数学八年级上册 12.2 三角形全等的判定 学案(含答案)
文档属性
| 名称 | 人教版数学八年级上册 12.2 三角形全等的判定 学案(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-12 10:57:17 | ||
图片预览




文档简介
全等三角形的判定
【第一课时】
【学习目标】
1.经历三角形全等的判定的全过程,体会利用操作 归纳获得数学结论的过程。
2.掌握三角形全等的“边边边”条件,了解角形的稳定性。
3.通过对问题的共同探讨培养学生的协作能力。
【学习重点】
三角形全等的条件。
【学习难点】
寻求三角形全等的条件。
【学习准备】
阅读课本,解决下列问题:
1.画一个三角形与已知三角形的三边相等。
2.全等三角形判定方法“边边边”。
3.作一个角等于已知角。
【学习过程】
1. 叫做全等三角形
2.全等三角形的 和 相等
3.将△ABC沿直线BC平移,得到△DEF,说出你得到的结论,说明理由?
如果AB=5, ∠A=55°, ∠B=45°,那么DE= ,∠F= 。
课内探究
探究三角形全等的条件:阅读课本探究1之前,回答下面问题:
1. 思考:两个三角形,有三条对应边,三个对应角,如果满足这六个条件中的一个或两个相等时,能不能保证所画出的两个三角形一定全等?
2. 只给一个条件。
(1)只给一条边时; (2)只给一个角时
结论:只有一条边或一个角对应相等的两个三角形 全等(填“一定”或“不一定”)
3、给出两个条件
(1)给出两个角相等: (2)给出两条边相等
结论:两个角对应相等的两个三角形 全等(填“一定”或“不一定”)
结论:两条边对应相等的两个三角形 全等(填“一定”或“不一定”)
(3)给出一边一角相等:
结论:一条边一个角对应相等的两个三角形 全等(填“一定”或“不一定”)
总结:只给出一个或两个条件时,都不能保证所画的三角形全等。
(4)如果两个三角形有三个条件对应相等,这两个三角形全等吗?我们也可以分情况讨论,有哪几种情况?
你觉得总共有几种情况,分别是
①我们先来探究两个三角形三个角对应相等的情况:
结论:两个三角形的三个角对应相等,这两个三角形 全等(填“一定”或“不一定”)
【拓展延伸】
已知AD=BC,AB=CD,求证:∠A=∠C
当堂检测
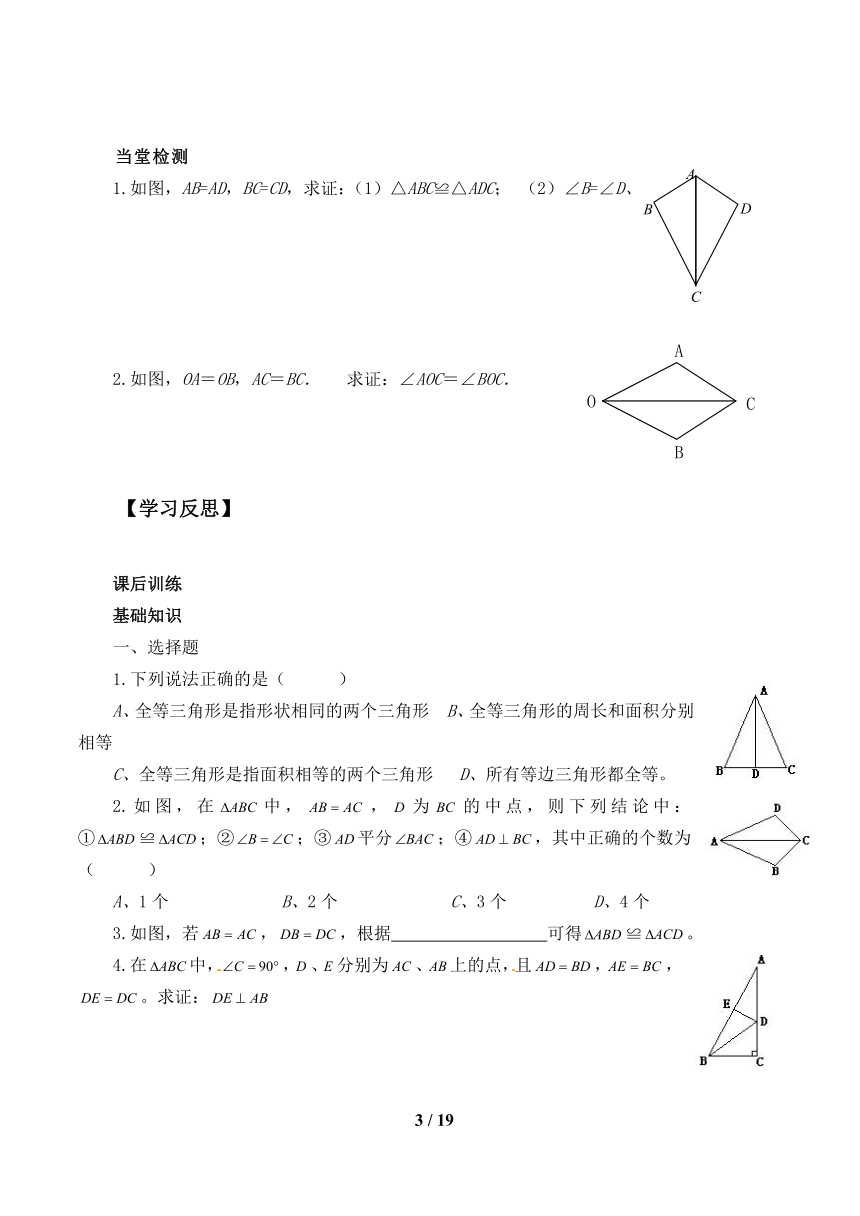
1.如图,AB=AD,BC=CD,求证:(1)△ABC≌△ADC; (2)∠B=∠D、
2.如图,OA=OB,AC=BC. 求证:∠AOC=∠BOC.
【学习反思】
课后训练
基础知识
一、选择题
1.下列说法正确的是( )
A、全等三角形是指形状相同的两个三角形 B、全等三角形的周长和面积分别相等
C、全等三角形是指面积相等的两个三角形 D、所有等边三角形都全等。
2.如图,在中,,为的中点,则下列结论中:①≌;②;③平分;④,其中正确的个数为( )
A、1个 B、2个 C、3个 D、4个
3.如图,若,,根据 可得≌。
4.在中,,、分别为、上的点,且,,。求证:
5.如图,点、、、在同一直线上,,,
求证:
6.如图,已知,,求证:。
1. 如图,已知点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF。
求证:△ABC≌△DEF
变式训练1: 已知点B、C、E、D在同一条直线上,AB=DF,AC=EF,BE= CD,
求证:AC∥EF
变式训练2: 已知AB=AD,AC=AE,BC =DE求证:∠BAD=∠CAE
【第二课时】
【学习目标】
1.经历三角形全等的判定的全过程,体会利用操作 归纳获得数学结论的过程。
2.掌握三角形全等的“边角边”条件。
3.在探索三角形全等及运用的过程培养学生的分析推理及简单的证明的能力。
【学习重点】
三角形全等的条件——边角边。
【学习难点】
寻求三角形全等的条件。
【学习准备】
阅读课本,解决下列问题:
问题: 如果已经知道两边一内角那么它有几种可能情况?(两种——两边及夹角或两边及一边的对角)
1.以两条线段(3cm,4cm)和一个角(45°)画一个三角形,使该角恰为这两条线段的夹角。
参考步骤:(要想一想这么画的道理哦)
(1)画一线段AB使它的长度等于4cm。
(2)以点A为顶点,作∠BAP=45°,在射线AP上截取AC=3cm,
(3)连结BC,△ABC即为所求。
2.把你画的三角形与其他同学画的三角形进行比较,所有的三角形都全等吗?
3.换两条线段和一个角,用同样的方法试试,是否有同样的结论?
结论:两边及其夹角相等,两个三角形一定全等。
4.这样我们就得到判定三角形全等的另一种方法(SAS):
(1)内容:___和它们的___对应相等的两个三角形全等。
课内探究
我们知道,两边和它们的夹角对应相等的两个三角形全等。由“两边及其中一边的对角对应相等”的条件例如两条边长度分别为2厘米,3厘米,长度为2厘米的边所对的角为30゜能判定两个三角形全等吗?
结论:两边及其一边所对的角相等,两个三角形不一定全等。
例 如图,△ABC中,AB=AC,AD平分∠BAC,试说明△ABD≌△ACD、
练一练 根据题目条件,判断下面的四组三角形是否一定全等?
(1) (2) (3) (4)
【拓展延伸】
1.已知:如图AB=AC,AD=AE,∠BAC=∠DAE
求证:(1) △ABD≌△ACE (2) ∠ADB= ∠AEC
当堂检测
练习
如图,AB=CB, ∠ABD=∠CBD, △ABD与△CBD全等吗?
解:在△ABD与△CBD中
AB=CB (已知)
∠ABD=∠CBD (已知)
=
△ABD≌△CBD ( )
变式1如上图,AB=CB,BD平分∠ADC, △ABD与△CBD全等吗?
变式2如上图,AD=CD 。BD平分∠ADC, △ABD与△CBD全等吗?
变式3如上图,AD=CD 。BD平分∠ADC, ∠A=∠C吗?
【学习反思】
课后训练
基础知识
1.如右图:OA=OD,OB=OC,求证:△ABO≌△DCO
证明:在△ABO和△DCO中
OA=OD
= ( )
OB=OC
∴△ABO≌△DCO( )
2.如右图:已知AB=DC,∠ABC=∠DCB,求证:AC=BD
证明:在△BCD和△BCA
AB=DC,
∠ABC=∠DCB( )
BC=________ ( )
∴△BCD≌ ( )
∴AC=________( )
3.具有下列条件的两个等腰三角形,不能判定它们全等的是( )
A、顶角、一腰对应相等 B、底边、一腰对应相等
C、两腰对应相等 D、一腰、一底角、一底边对应相等
4.如图,下列条件中能使≌的是( )
A、, B、,
C、, D、,
5.如图,线段、互相平分交于点,则下列结论错误的是( )
A、 B、 C、 D、
6.如图,已知,。求证:≌
7.点、、、在同一直线上,,AE=BC且。
求证:⑴≌ ⑵
8.如图,于,于,,。
求证:
【第三课时】
【学习目标】
1.经历三角形全等的判定的全过程,体会利用操作 归纳获得数学结论的过程。
2.掌握三角形全等的“角边角”条件
【学习重点】
三角形全等的条件——角边角。
【学习难点】
寻求三角形全等的条件
【学习准备】
阅读课本,解决下列问题:
三角形全等的判定方法:ASA AAS
【自能学习】
一、做一做。
1.已知两个角(30°,45°)和一条线段(3cm),以这两个角为内角,以这条线段为这两个角的夹边,画一个三角形。
思考:1)把你画的三角形与其他同学画的进行比较,所有的三角形都全等吗?
2)换两个角和一条线段,用同样的方法试试看,是否有同样的结论?
结论:两角及夹边相等,两个三角形一定全等。
2.由此又得到一个全等三角形的判定方法(ASA):
三角形全等的判定方法:ASA AAS
(1) ASA 内容; ___和它们的___对应相等的两个三角形全等。
(2)简写:“___”或“___”
(3)书写格式
在△ABC和△DEF中
∠A=∠D
AB=__
∠B = __
∴ △ABC≌___ (___)
课内探究
如图,如果两个三角形有两个角及其中一个角的对边分别对应相等,那么这两个三角形是否一定全等?
你的结论是______________________________,你能证明吗?
证明:
【拓展延伸】
如图,在△ABC中,∠B=2∠C,AD是△ABC的角平分线,
∠1=∠C,求证AC=AB+CE
当堂检测
1.如下图,D在AB上,E在AC上,AB=AC,∠B=∠C
求证:AD=AE。
2.已知:点D在AB上,点E在AC上, BE⊥AC, CD⊥AB,AB=AC,求证:BD=CE
【学习反思】
课后训练
基础知识
1.下列说法中,正确的是( )
A、所有的等腰三角形全等 B、有两边对应相等的两个等腰三角形全等
C、有一边对应相等的两个等腰三角形全等 D、腰和顶角对应相等的两个等腰三角形全等
2.在△ABC与△A′B′C′中,已知∠A=44°,∠B=67°,∠C′=69°,∠A′=44°,且AC=A′C′,那么这两个三角形( )
A、一定不全等 B、一定全等 C、不一定全等 D、以上都不对
3.如图,和中,下列能判定≌的是( )
A、,, B、,,
C、,, D、,,
4.如图为打碎的一块三角形玻璃,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是( )
A、带①去 B、带②去 C、带③去 D、带①和②去
5、在△ABC和△DEF中,条件(1)AB=DE,(2)BC=EF,(3)AC=DF,(4) ∠A=∠D,(5) ∠B=∠E,(6) ∠C=∠F,则下列各组条件中,不能保证△ABC≌△DEF的是( )
A、(1) (2) (3) B、(1) (2) (5)
C、(1) (3) (5) D、(2) (5) (6)
6、如图,,,则图中全等三角形有( )
A、1对 B、2对 C、3对 D、4对
7.如图,于,于,平分,则图中
全等三角形有( )
A、1对 B、2对 C、3对 D、4对
8、如图,已知,,求证:
9.满足下列哪种条件时,就能判定△ABC≌△DEF ( )
A. AB=DE,BC=EF, ∠A=∠E; B. AB=DE,BC=EF, ∠C=∠F
C. ∠A=∠E,AB=EF, ∠B=∠D; D. ∠A=∠D,AB=DE, ∠B=∠E
10.如图所示,已知∠A=∠D,∠1=∠2,那么要
得到△ABC≌△DEF,还应给出的条件是:( )
A. ∠B=∠E B.ED=BC
C. AB=EF D.AF=CD
11.如6题图, 在△ABC和△DEF中,AF=DC, ∠A=∠D,
当_____________时,可根据“ASA”证明△ABC≌△DEF
【第四课时】
【学习目标】
1.经历直角三角形全等的判定的全过程,体会利用操作 归纳获得数学结论的过程。
2.掌握直角三角形全等的“斜边直角边”条件。
3.在探索三角形全等及运用的过程培养学生的分析推理及简单的证明的能力。
【学习重点】
三角形全等的条件——斜边直角边。
【学习难点】
寻求直角三角形全等的条件。
【学习准备】
阅读课本,解决下列问题:三角形全等的判定方法:HL
复习思考
(1)、判定两个三角形全等的方法: 、 、 、
(2)、如图,Rt△ABC中,直角边是 、 ,斜边是
(3)、如图,AB⊥BE于B,DE⊥BE于E,
①若∠A=∠D,AB=DE,
则△ABC与△DEF (填“全等”或“不全等” )
根据 (用简写法)
②若∠A=∠D,BC=EF,
则△ABC与△DEF (填“全等”或“不全等” )
根据 (用简写法)
③若AB=DE,BC=EF,
则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)
④若AB=DE,BC=EF,AC=DF
则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)
课内探究
1.如果两个直角三角形满足斜边和一条直角边对应相等,这两个直角三角形全等吗?
(1)动手试一试。
已知:Rt△ABC
求作:Rt△, 使=90°, =AB, =BC
作法:
(2) 把△剪下来放到△ABC上,观察△与△ABC是否能够完全重合?
(3)归纳;由上面的画图和实验可以得到判定两个直角三角形全等的一个方法
斜边与一直角边对应相等的两个直角三角形 (可以简写成“ ”或“ ”)
(4)用数学语言表述上面的判定方法
在Rt△ABC和Rt中,
∵ ∴Rt△ABC≌Rt△
(5)直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法 “ ”、
“ ”、 “ ”、 “ ”、 还有直角三角形特殊的判定方法 “ ”
2.如图,AC=AD,∠C,∠D是直角,将上述条件标注在图中,
你能说明BC与BD相等吗?
【拓展延伸】
1.如图,点、、、在同一条直线上,,,,
且,求证:
2.如图,、、、在同一条直线上,于,于,,。
探究与的关系,并说明理由。
当堂检测
1.如图,CE⊥AB,DF⊥AB,垂足分别为E、F,
(1)若AC//DB,且AC=DB,则△ACE≌△BDF,根据
(2)若AC//DB,且AE=BF,则△ACE≌△BDF,根据
(3)若AE=BF,且CE=DF,则△ACE≌△BDF,根据
(4)若AC=BD,AE=BF,CE=DF。则△ACE≌△BDF,根据
(5) 若AC=BD,CE=DF(或AE=BF),则△ACE≌△BDF,根据
2.如图,△ABC中,AB=AC,AD是高,则△ADB与△ADC
(填“全等”或“不全等” )根据 (用简写法)
3.判断两个直角三角形全等的方法不正确的有( )
A、两条直角边对应相等 B、斜边和一锐角对应相等
C、斜边和一条直角边对应相等 D、两个锐角对应相等
4.如图,B、E、F、C在同一直线上,AF⊥BC于F,DE⊥BC于E,
AB=DC,BE=CF,你认为AB平行于CD吗?说说你的理由
答:AB平行于CD
理由:∵ AF⊥BC,DE⊥BC (已知)
∴ ∠AFB=∠DEC= °(垂直的定义)
∵BE=CF,∴BF=CE
在Rt△ 和Rt△ 中
∵∴ ≌
( )
∴ = ( )
∴ (内错角相等,两直线平行)
【课后反思】
课后训练
基础知识
1.下列命题中正确的有( )
①两直角边对应相等的两直角三角形全等;
②两锐角对应相等的两直角三角形全等;
③斜边和一条直角边对应相等的两直角三角形全等;
④一锐角和斜边对应相等的两直角三角形全等。
A、2个 B、3个 C、4个 D、1个
2.如图,和中,,,点、、、
在同一条直线上,再增加一个条件,不能判定≌的是( )
A、 B、 C、 D、
3.如图,,于,于,图中全等三角形的组数是( )
A、2 B、3 C、4 D、5
4.如图,于,于,,。
求证:
1.已知: AC⊥BC,BD⊥AD,AC=BD. 求证: BC=AD.
如图,于,于,且,求证:。
【第五课时】
【学习目标】
1.进一步掌握三角形全等的条件
2.在解决问题的过程培养学生的分析推理及简单的证明的能力
【学习重点】
三角形全等的条件的应用。
【学习难点】
三角形全等的条件的应用。
【课前预习】
一、知识要点回顾。
1.全等三角形的概念: 的两个三角形叫做全等三角形。
2.全等三角形的性质:全等三角形的对应边 ,对应角 。
3.全等三角形的判定:(1)一般三角形全等的判定: 。
(2)直角三角形全等的判定: 。
注意(1)“分别对应相等”是关键。
(2)两边及其中一边的对角分别对应相等的两个三角形不一定全等。
课内探究
三角形全等判定的思路
1.如图1,已知△ABC和△DCB中,AB=DC,请补充一个条件 ,使△ABC≌△DCB.
2.如图2,已知∠C=∠D,要判定△ABC≌△ABD,需要添加的一个条件是 。
3.如图3,已知∠1=∠2要要判定△ABC≌△CDA, 需要添加的一个条件是 。
4.如图4,已知∠B=∠E,要判定△ABC≌△AED,需要添加的一个条件是 。
【拓展延伸】
1.判断题:
(1)一个锐角和这个锐角的对边对应相等的两个直角三角形全等。( )
(2)一个锐角和锐角相邻的一直角边对应相等的两个直角三角形全等( )
(3)一个锐角与一斜边对应相等的两个直角三角形全等( )
(4)两直角边对应相等的两个直角三角形全等( )
(5)两边对应相等的两个直角三角形全等( )
(6)两锐角对应相等的两个直角三角形全等( )
(7)一个锐角与一边对应相等的两个直角三角形全等( )
(8)一直角边和斜边上的高对应相等的两个直角三角形全等( )
2.已知,如图7,C为BE上一点,点A,D分别在BE两侧,
AB∥ED,AB=CE,BC=ED求证:AC=CD
当堂检测
1.已知;如图5,B、C、E三点在同一直线上,AC∥DE,AC=CE, ∠ACD=∠B,
求证:△ABC≌△CDE
2.如图6,AB⊥BC,AD⊥DC,AB=AD,求证:∠1=∠2.
【学习反思】
课后训练
基础知识
1.下列给出的四组条件中,能判定≌的是( )
A、,,
B、,,
C、,,
D、, , 周长=周
2.若≌,且的周长为20,,,则长为( )
A、5 B、8 C、7 D、5或8
3.如图,在上,在上,且,那么补充下列一个条件后,仍无法判定≌的是( )
A、 B、 C、 D、
4.如图,将两根钢条、的中点连在一起,使、可以绕着点自由转动,就做成了一个测量工件,则的长等于内槽宽,那么判定≌的理由是( )
A、边角边 B、角边角 C、边边边 D、角角边
5.在和中,,,,,且,那么这两个三角形( )
A、一定不全等 B、一定全等
C、不一定全等 D、以上都不对
6.如图,若≌,则等于( )
A、30° B、50° C、60° D、100°
7.已知,,,请问图中有哪几对全等三角形?并任选其中一对给予证明。
8.如图,,,于,于。求证:。
9.如图, 已知:AB⊥BC于B , EF⊥AC于G , DF⊥BC于D , BC=DF。求证:AC=EF。
300
700
800
300
800
700
A
B
C
D
A F C D
1
2
E
B
A
B
C
A1
B1
C1
PAGE
19 / 19
【第一课时】
【学习目标】
1.经历三角形全等的判定的全过程,体会利用操作 归纳获得数学结论的过程。
2.掌握三角形全等的“边边边”条件,了解角形的稳定性。
3.通过对问题的共同探讨培养学生的协作能力。
【学习重点】
三角形全等的条件。
【学习难点】
寻求三角形全等的条件。
【学习准备】
阅读课本,解决下列问题:
1.画一个三角形与已知三角形的三边相等。
2.全等三角形判定方法“边边边”。
3.作一个角等于已知角。
【学习过程】
1. 叫做全等三角形
2.全等三角形的 和 相等
3.将△ABC沿直线BC平移,得到△DEF,说出你得到的结论,说明理由?
如果AB=5, ∠A=55°, ∠B=45°,那么DE= ,∠F= 。
课内探究
探究三角形全等的条件:阅读课本探究1之前,回答下面问题:
1. 思考:两个三角形,有三条对应边,三个对应角,如果满足这六个条件中的一个或两个相等时,能不能保证所画出的两个三角形一定全等?
2. 只给一个条件。
(1)只给一条边时; (2)只给一个角时
结论:只有一条边或一个角对应相等的两个三角形 全等(填“一定”或“不一定”)
3、给出两个条件
(1)给出两个角相等: (2)给出两条边相等
结论:两个角对应相等的两个三角形 全等(填“一定”或“不一定”)
结论:两条边对应相等的两个三角形 全等(填“一定”或“不一定”)
(3)给出一边一角相等:
结论:一条边一个角对应相等的两个三角形 全等(填“一定”或“不一定”)
总结:只给出一个或两个条件时,都不能保证所画的三角形全等。
(4)如果两个三角形有三个条件对应相等,这两个三角形全等吗?我们也可以分情况讨论,有哪几种情况?
你觉得总共有几种情况,分别是
①我们先来探究两个三角形三个角对应相等的情况:
结论:两个三角形的三个角对应相等,这两个三角形 全等(填“一定”或“不一定”)
【拓展延伸】
已知AD=BC,AB=CD,求证:∠A=∠C
当堂检测
1.如图,AB=AD,BC=CD,求证:(1)△ABC≌△ADC; (2)∠B=∠D、
2.如图,OA=OB,AC=BC. 求证:∠AOC=∠BOC.
【学习反思】
课后训练
基础知识
一、选择题
1.下列说法正确的是( )
A、全等三角形是指形状相同的两个三角形 B、全等三角形的周长和面积分别相等
C、全等三角形是指面积相等的两个三角形 D、所有等边三角形都全等。
2.如图,在中,,为的中点,则下列结论中:①≌;②;③平分;④,其中正确的个数为( )
A、1个 B、2个 C、3个 D、4个
3.如图,若,,根据 可得≌。
4.在中,,、分别为、上的点,且,,。求证:
5.如图,点、、、在同一直线上,,,
求证:
6.如图,已知,,求证:。
1. 如图,已知点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF。
求证:△ABC≌△DEF
变式训练1: 已知点B、C、E、D在同一条直线上,AB=DF,AC=EF,BE= CD,
求证:AC∥EF
变式训练2: 已知AB=AD,AC=AE,BC =DE求证:∠BAD=∠CAE
【第二课时】
【学习目标】
1.经历三角形全等的判定的全过程,体会利用操作 归纳获得数学结论的过程。
2.掌握三角形全等的“边角边”条件。
3.在探索三角形全等及运用的过程培养学生的分析推理及简单的证明的能力。
【学习重点】
三角形全等的条件——边角边。
【学习难点】
寻求三角形全等的条件。
【学习准备】
阅读课本,解决下列问题:
问题: 如果已经知道两边一内角那么它有几种可能情况?(两种——两边及夹角或两边及一边的对角)
1.以两条线段(3cm,4cm)和一个角(45°)画一个三角形,使该角恰为这两条线段的夹角。
参考步骤:(要想一想这么画的道理哦)
(1)画一线段AB使它的长度等于4cm。
(2)以点A为顶点,作∠BAP=45°,在射线AP上截取AC=3cm,
(3)连结BC,△ABC即为所求。
2.把你画的三角形与其他同学画的三角形进行比较,所有的三角形都全等吗?
3.换两条线段和一个角,用同样的方法试试,是否有同样的结论?
结论:两边及其夹角相等,两个三角形一定全等。
4.这样我们就得到判定三角形全等的另一种方法(SAS):
(1)内容:___和它们的___对应相等的两个三角形全等。
课内探究
我们知道,两边和它们的夹角对应相等的两个三角形全等。由“两边及其中一边的对角对应相等”的条件例如两条边长度分别为2厘米,3厘米,长度为2厘米的边所对的角为30゜能判定两个三角形全等吗?
结论:两边及其一边所对的角相等,两个三角形不一定全等。
例 如图,△ABC中,AB=AC,AD平分∠BAC,试说明△ABD≌△ACD、
练一练 根据题目条件,判断下面的四组三角形是否一定全等?
(1) (2) (3) (4)
【拓展延伸】
1.已知:如图AB=AC,AD=AE,∠BAC=∠DAE
求证:(1) △ABD≌△ACE (2) ∠ADB= ∠AEC
当堂检测
练习
如图,AB=CB, ∠ABD=∠CBD, △ABD与△CBD全等吗?
解:在△ABD与△CBD中
AB=CB (已知)
∠ABD=∠CBD (已知)
=
△ABD≌△CBD ( )
变式1如上图,AB=CB,BD平分∠ADC, △ABD与△CBD全等吗?
变式2如上图,AD=CD 。BD平分∠ADC, △ABD与△CBD全等吗?
变式3如上图,AD=CD 。BD平分∠ADC, ∠A=∠C吗?
【学习反思】
课后训练
基础知识
1.如右图:OA=OD,OB=OC,求证:△ABO≌△DCO
证明:在△ABO和△DCO中
OA=OD
= ( )
OB=OC
∴△ABO≌△DCO( )
2.如右图:已知AB=DC,∠ABC=∠DCB,求证:AC=BD
证明:在△BCD和△BCA
AB=DC,
∠ABC=∠DCB( )
BC=________ ( )
∴△BCD≌ ( )
∴AC=________( )
3.具有下列条件的两个等腰三角形,不能判定它们全等的是( )
A、顶角、一腰对应相等 B、底边、一腰对应相等
C、两腰对应相等 D、一腰、一底角、一底边对应相等
4.如图,下列条件中能使≌的是( )
A、, B、,
C、, D、,
5.如图,线段、互相平分交于点,则下列结论错误的是( )
A、 B、 C、 D、
6.如图,已知,。求证:≌
7.点、、、在同一直线上,,AE=BC且。
求证:⑴≌ ⑵
8.如图,于,于,,。
求证:
【第三课时】
【学习目标】
1.经历三角形全等的判定的全过程,体会利用操作 归纳获得数学结论的过程。
2.掌握三角形全等的“角边角”条件
【学习重点】
三角形全等的条件——角边角。
【学习难点】
寻求三角形全等的条件
【学习准备】
阅读课本,解决下列问题:
三角形全等的判定方法:ASA AAS
【自能学习】
一、做一做。
1.已知两个角(30°,45°)和一条线段(3cm),以这两个角为内角,以这条线段为这两个角的夹边,画一个三角形。
思考:1)把你画的三角形与其他同学画的进行比较,所有的三角形都全等吗?
2)换两个角和一条线段,用同样的方法试试看,是否有同样的结论?
结论:两角及夹边相等,两个三角形一定全等。
2.由此又得到一个全等三角形的判定方法(ASA):
三角形全等的判定方法:ASA AAS
(1) ASA 内容; ___和它们的___对应相等的两个三角形全等。
(2)简写:“___”或“___”
(3)书写格式
在△ABC和△DEF中
∠A=∠D
AB=__
∠B = __
∴ △ABC≌___ (___)
课内探究
如图,如果两个三角形有两个角及其中一个角的对边分别对应相等,那么这两个三角形是否一定全等?
你的结论是______________________________,你能证明吗?
证明:
【拓展延伸】
如图,在△ABC中,∠B=2∠C,AD是△ABC的角平分线,
∠1=∠C,求证AC=AB+CE
当堂检测
1.如下图,D在AB上,E在AC上,AB=AC,∠B=∠C
求证:AD=AE。
2.已知:点D在AB上,点E在AC上, BE⊥AC, CD⊥AB,AB=AC,求证:BD=CE
【学习反思】
课后训练
基础知识
1.下列说法中,正确的是( )
A、所有的等腰三角形全等 B、有两边对应相等的两个等腰三角形全等
C、有一边对应相等的两个等腰三角形全等 D、腰和顶角对应相等的两个等腰三角形全等
2.在△ABC与△A′B′C′中,已知∠A=44°,∠B=67°,∠C′=69°,∠A′=44°,且AC=A′C′,那么这两个三角形( )
A、一定不全等 B、一定全等 C、不一定全等 D、以上都不对
3.如图,和中,下列能判定≌的是( )
A、,, B、,,
C、,, D、,,
4.如图为打碎的一块三角形玻璃,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是( )
A、带①去 B、带②去 C、带③去 D、带①和②去
5、在△ABC和△DEF中,条件(1)AB=DE,(2)BC=EF,(3)AC=DF,(4) ∠A=∠D,(5) ∠B=∠E,(6) ∠C=∠F,则下列各组条件中,不能保证△ABC≌△DEF的是( )
A、(1) (2) (3) B、(1) (2) (5)
C、(1) (3) (5) D、(2) (5) (6)
6、如图,,,则图中全等三角形有( )
A、1对 B、2对 C、3对 D、4对
7.如图,于,于,平分,则图中
全等三角形有( )
A、1对 B、2对 C、3对 D、4对
8、如图,已知,,求证:
9.满足下列哪种条件时,就能判定△ABC≌△DEF ( )
A. AB=DE,BC=EF, ∠A=∠E; B. AB=DE,BC=EF, ∠C=∠F
C. ∠A=∠E,AB=EF, ∠B=∠D; D. ∠A=∠D,AB=DE, ∠B=∠E
10.如图所示,已知∠A=∠D,∠1=∠2,那么要
得到△ABC≌△DEF,还应给出的条件是:( )
A. ∠B=∠E B.ED=BC
C. AB=EF D.AF=CD
11.如6题图, 在△ABC和△DEF中,AF=DC, ∠A=∠D,
当_____________时,可根据“ASA”证明△ABC≌△DEF
【第四课时】
【学习目标】
1.经历直角三角形全等的判定的全过程,体会利用操作 归纳获得数学结论的过程。
2.掌握直角三角形全等的“斜边直角边”条件。
3.在探索三角形全等及运用的过程培养学生的分析推理及简单的证明的能力。
【学习重点】
三角形全等的条件——斜边直角边。
【学习难点】
寻求直角三角形全等的条件。
【学习准备】
阅读课本,解决下列问题:三角形全等的判定方法:HL
复习思考
(1)、判定两个三角形全等的方法: 、 、 、
(2)、如图,Rt△ABC中,直角边是 、 ,斜边是
(3)、如图,AB⊥BE于B,DE⊥BE于E,
①若∠A=∠D,AB=DE,
则△ABC与△DEF (填“全等”或“不全等” )
根据 (用简写法)
②若∠A=∠D,BC=EF,
则△ABC与△DEF (填“全等”或“不全等” )
根据 (用简写法)
③若AB=DE,BC=EF,
则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)
④若AB=DE,BC=EF,AC=DF
则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)
课内探究
1.如果两个直角三角形满足斜边和一条直角边对应相等,这两个直角三角形全等吗?
(1)动手试一试。
已知:Rt△ABC
求作:Rt△, 使=90°, =AB, =BC
作法:
(2) 把△剪下来放到△ABC上,观察△与△ABC是否能够完全重合?
(3)归纳;由上面的画图和实验可以得到判定两个直角三角形全等的一个方法
斜边与一直角边对应相等的两个直角三角形 (可以简写成“ ”或“ ”)
(4)用数学语言表述上面的判定方法
在Rt△ABC和Rt中,
∵ ∴Rt△ABC≌Rt△
(5)直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法 “ ”、
“ ”、 “ ”、 “ ”、 还有直角三角形特殊的判定方法 “ ”
2.如图,AC=AD,∠C,∠D是直角,将上述条件标注在图中,
你能说明BC与BD相等吗?
【拓展延伸】
1.如图,点、、、在同一条直线上,,,,
且,求证:
2.如图,、、、在同一条直线上,于,于,,。
探究与的关系,并说明理由。
当堂检测
1.如图,CE⊥AB,DF⊥AB,垂足分别为E、F,
(1)若AC//DB,且AC=DB,则△ACE≌△BDF,根据
(2)若AC//DB,且AE=BF,则△ACE≌△BDF,根据
(3)若AE=BF,且CE=DF,则△ACE≌△BDF,根据
(4)若AC=BD,AE=BF,CE=DF。则△ACE≌△BDF,根据
(5) 若AC=BD,CE=DF(或AE=BF),则△ACE≌△BDF,根据
2.如图,△ABC中,AB=AC,AD是高,则△ADB与△ADC
(填“全等”或“不全等” )根据 (用简写法)
3.判断两个直角三角形全等的方法不正确的有( )
A、两条直角边对应相等 B、斜边和一锐角对应相等
C、斜边和一条直角边对应相等 D、两个锐角对应相等
4.如图,B、E、F、C在同一直线上,AF⊥BC于F,DE⊥BC于E,
AB=DC,BE=CF,你认为AB平行于CD吗?说说你的理由
答:AB平行于CD
理由:∵ AF⊥BC,DE⊥BC (已知)
∴ ∠AFB=∠DEC= °(垂直的定义)
∵BE=CF,∴BF=CE
在Rt△ 和Rt△ 中
∵∴ ≌
( )
∴ = ( )
∴ (内错角相等,两直线平行)
【课后反思】
课后训练
基础知识
1.下列命题中正确的有( )
①两直角边对应相等的两直角三角形全等;
②两锐角对应相等的两直角三角形全等;
③斜边和一条直角边对应相等的两直角三角形全等;
④一锐角和斜边对应相等的两直角三角形全等。
A、2个 B、3个 C、4个 D、1个
2.如图,和中,,,点、、、
在同一条直线上,再增加一个条件,不能判定≌的是( )
A、 B、 C、 D、
3.如图,,于,于,图中全等三角形的组数是( )
A、2 B、3 C、4 D、5
4.如图,于,于,,。
求证:
1.已知: AC⊥BC,BD⊥AD,AC=BD. 求证: BC=AD.
如图,于,于,且,求证:。
【第五课时】
【学习目标】
1.进一步掌握三角形全等的条件
2.在解决问题的过程培养学生的分析推理及简单的证明的能力
【学习重点】
三角形全等的条件的应用。
【学习难点】
三角形全等的条件的应用。
【课前预习】
一、知识要点回顾。
1.全等三角形的概念: 的两个三角形叫做全等三角形。
2.全等三角形的性质:全等三角形的对应边 ,对应角 。
3.全等三角形的判定:(1)一般三角形全等的判定: 。
(2)直角三角形全等的判定: 。
注意(1)“分别对应相等”是关键。
(2)两边及其中一边的对角分别对应相等的两个三角形不一定全等。
课内探究
三角形全等判定的思路
1.如图1,已知△ABC和△DCB中,AB=DC,请补充一个条件 ,使△ABC≌△DCB.
2.如图2,已知∠C=∠D,要判定△ABC≌△ABD,需要添加的一个条件是 。
3.如图3,已知∠1=∠2要要判定△ABC≌△CDA, 需要添加的一个条件是 。
4.如图4,已知∠B=∠E,要判定△ABC≌△AED,需要添加的一个条件是 。
【拓展延伸】
1.判断题:
(1)一个锐角和这个锐角的对边对应相等的两个直角三角形全等。( )
(2)一个锐角和锐角相邻的一直角边对应相等的两个直角三角形全等( )
(3)一个锐角与一斜边对应相等的两个直角三角形全等( )
(4)两直角边对应相等的两个直角三角形全等( )
(5)两边对应相等的两个直角三角形全等( )
(6)两锐角对应相等的两个直角三角形全等( )
(7)一个锐角与一边对应相等的两个直角三角形全等( )
(8)一直角边和斜边上的高对应相等的两个直角三角形全等( )
2.已知,如图7,C为BE上一点,点A,D分别在BE两侧,
AB∥ED,AB=CE,BC=ED求证:AC=CD
当堂检测
1.已知;如图5,B、C、E三点在同一直线上,AC∥DE,AC=CE, ∠ACD=∠B,
求证:△ABC≌△CDE
2.如图6,AB⊥BC,AD⊥DC,AB=AD,求证:∠1=∠2.
【学习反思】
课后训练
基础知识
1.下列给出的四组条件中,能判定≌的是( )
A、,,
B、,,
C、,,
D、, , 周长=周
2.若≌,且的周长为20,,,则长为( )
A、5 B、8 C、7 D、5或8
3.如图,在上,在上,且,那么补充下列一个条件后,仍无法判定≌的是( )
A、 B、 C、 D、
4.如图,将两根钢条、的中点连在一起,使、可以绕着点自由转动,就做成了一个测量工件,则的长等于内槽宽,那么判定≌的理由是( )
A、边角边 B、角边角 C、边边边 D、角角边
5.在和中,,,,,且,那么这两个三角形( )
A、一定不全等 B、一定全等
C、不一定全等 D、以上都不对
6.如图,若≌,则等于( )
A、30° B、50° C、60° D、100°
7.已知,,,请问图中有哪几对全等三角形?并任选其中一对给予证明。
8.如图,,,于,于。求证:。
9.如图, 已知:AB⊥BC于B , EF⊥AC于G , DF⊥BC于D , BC=DF。求证:AC=EF。
300
700
800
300
800
700
A
B
C
D
A F C D
1
2
E
B
A
B
C
A1
B1
C1
PAGE
19 / 19
