人教版数学8年级上册 12.2 三角形全等的判定学案(含答案)
文档属性
| 名称 | 人教版数学8年级上册 12.2 三角形全等的判定学案(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 168.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-12 11:59:07 | ||
图片预览


文档简介
三角形全等的判定——巩固课(1)
班级: 组号: 姓名:
一、巩固训练
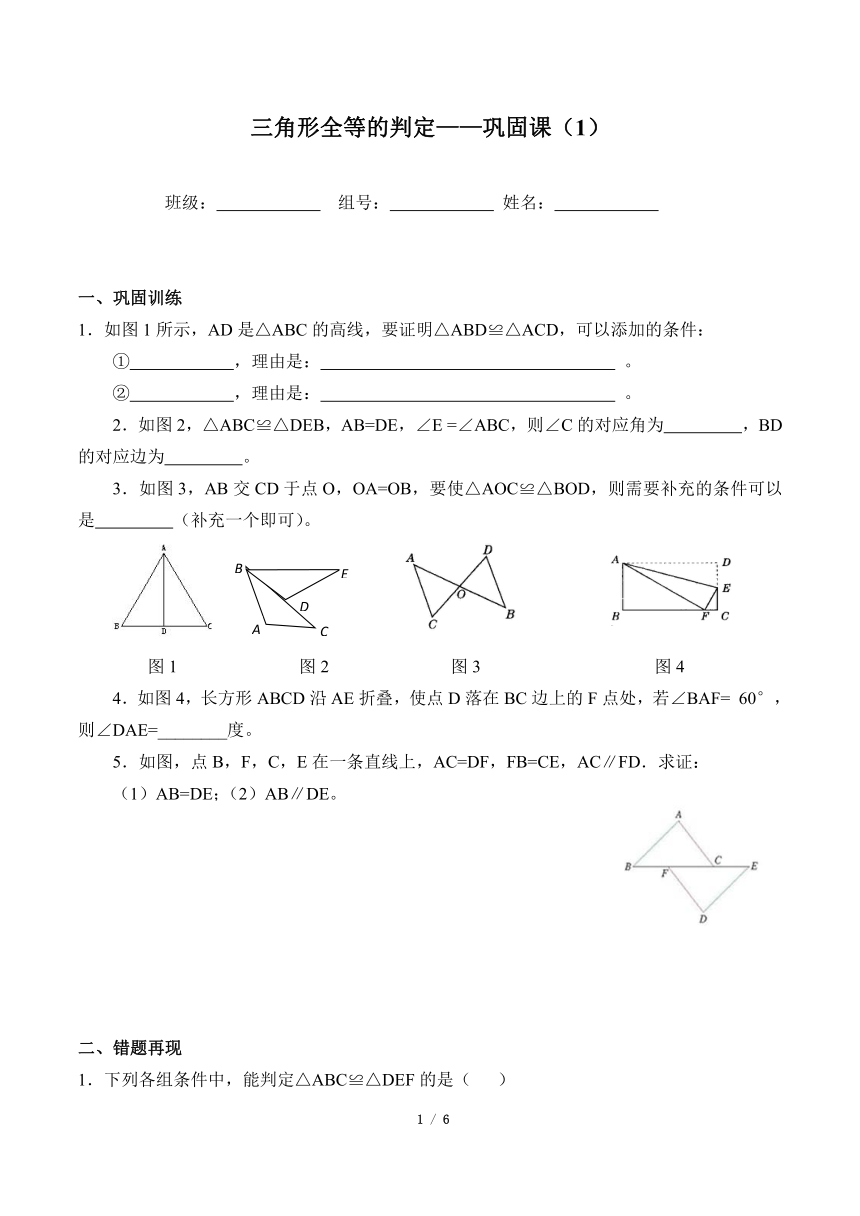
1.如图1所示,AD是△ABC的高线,要证明△ABD≌△ACD,可以添加的条件:
① ,理由是: 。
② ,理由是: 。
2.如图2,△ABC≌△DEB,AB=DE,∠E =∠ABC,则∠C的对应角为 ,BD的对应边为 。
3.如图3,AB交CD于点O,OA=OB,要使△AOC≌△BOD,则需要补充的条件可以是 (补充一个即可)。
图1 图2 图3 图4
4.如图4,长方形ABCD沿AE折叠,使点D落在BC边上的F点处,若∠BAF=60°,则∠DAE=________度。
5.如图,点B,F,C,E在一条直线上,AC=DF,FB=CE,AC∥FD.求证:
(1)AB=DE;(2)AB∥DE。
二、错题再现
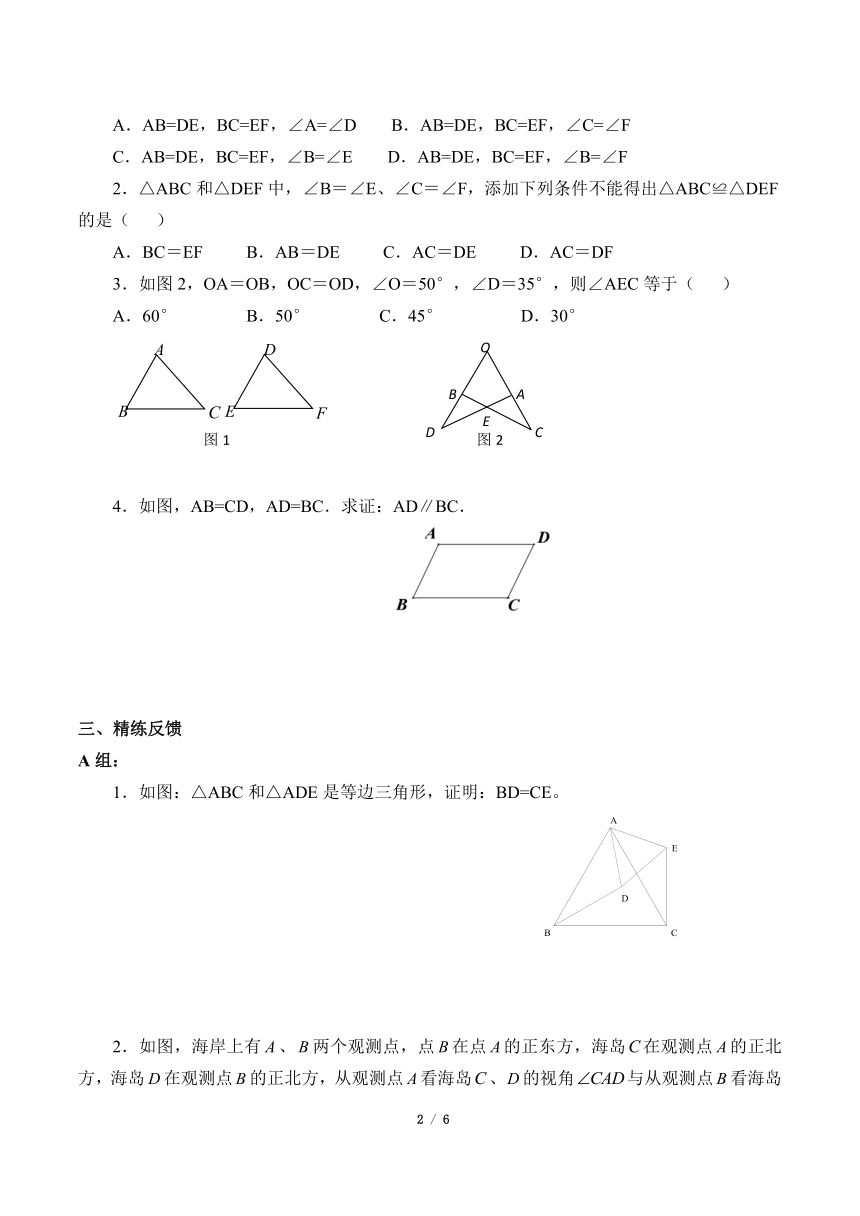
1.下列各组条件中,能判定△ABC≌△DEF的是( )
A.AB=DE,BC=EF,∠A=∠D B.AB=DE,BC=EF,∠C=∠F
C.AB=DE,BC=EF,∠B=∠E D.AB=DE,BC=EF,∠B=∠F
2.△ABC和△DEF中,∠B=∠E、∠C=∠F,添加下列条件不能得出△ABC≌△DEF的是( )
A.BC=EF B.AB=DE C.AC=DE D.AC=DF
3.如图2,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠AEC等于( )
A.60° B.50° C.45° D.30°
4.如图,AB=CD,AD=BC.求证:AD∥BC.
三、精练反馈
A组:
1.如图:△ABC和△ADE是等边三角形,证明:BD=CE。
2.如图,海岸上有、两个观测点,点在点的正东方,海岛在观测点的正北方,海岛在观测点的正北方,从观测点看海岛、的视角与从观测点看海岛、的视角相等。那么海岛、到观测点、所在海岸的距离相等。为什么?
B组:
在△ABC中,AC=BC,∠ACB=90°,直线经过点,且于,于。(1)当直线绕点旋转到图1的位置时,求证:
①≌;②;
(2)当直线绕点旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由。
【答案】
巩固训练
1.①DB=DC SAS ②∠B=∠C SSS
2.∠DBE AC
3.CO=DO
4.15
5.证明:(1)∵FB=CE ∴BF+FC=CE+FC ∴BC=EF ∵AC∥FD ∴∠ACB=∠DFE
在△ABC和△DEF中
∴△ABC≌△DEF(SAS)
∴AB=DE
(2)∵△ABC≌△DEF
∴∠B=∠E
∴AB∥DE
错题再现
1.C 2.C 3.A
4.证明:连接AC
在△ABC和△CDB中
∴△ABC≌△CDB(SSS) ∴ ∴AD∥BC
精练反馈
1.证明:
∵△ABC和△ADE是等边三角形
∴AB=AC AD=AE ∠BAC=∠DAE=60°
∴∠BAC-∠DAC=∠DAE-∠DAC
∴∠BAD=∠EAC
在△ABD和△EAC中
∴△ABD≌△EAC(SAS)
∴BD=CE
2.答:AC=BD
由题可知:
∠CAB=∠DBA ==90°
∴-∠CAB=-∠DBA
在△ABC和△DBA中
∴△ABC≌△DBA(ASA)
∴AC=BD
3.证明:
(1)①∵∠ACB=90°∴∠ACD+∠BCE=90°
∵ ∴∠DAC+∠DCA=90°∠ADC=90° ∴∠DAC=∠ECB
∵ ∴∠BEC=90°=∠ADC
在△ADC和△BCE中
∴△ADC≌△BCE(AAS)
②∵△ADC≌△BCE
∴DC=BE AD=EC
∴DE=DC+CE
∴DE=AD+BE
(2)答:不成立 DE=AD-BE
∵∠ACB=90° ∴∠ACD+∠BCE=90°
∵
∴∠DAC+∠DCA=90°∠ADC=90° ∴∠DAC=∠ECB
∵ ∴∠BEC=90°=∠ADC
在△ADC和△BCE中
∴△ADC≌△BCE(AAS)
∴DC=BE AD=EC
∵DE=CE-CD
∴DE=AD-BE
6 / 6
班级: 组号: 姓名:
一、巩固训练
1.如图1所示,AD是△ABC的高线,要证明△ABD≌△ACD,可以添加的条件:
① ,理由是: 。
② ,理由是: 。
2.如图2,△ABC≌△DEB,AB=DE,∠E =∠ABC,则∠C的对应角为 ,BD的对应边为 。
3.如图3,AB交CD于点O,OA=OB,要使△AOC≌△BOD,则需要补充的条件可以是 (补充一个即可)。
图1 图2 图3 图4
4.如图4,长方形ABCD沿AE折叠,使点D落在BC边上的F点处,若∠BAF=60°,则∠DAE=________度。
5.如图,点B,F,C,E在一条直线上,AC=DF,FB=CE,AC∥FD.求证:
(1)AB=DE;(2)AB∥DE。
二、错题再现
1.下列各组条件中,能判定△ABC≌△DEF的是( )
A.AB=DE,BC=EF,∠A=∠D B.AB=DE,BC=EF,∠C=∠F
C.AB=DE,BC=EF,∠B=∠E D.AB=DE,BC=EF,∠B=∠F
2.△ABC和△DEF中,∠B=∠E、∠C=∠F,添加下列条件不能得出△ABC≌△DEF的是( )
A.BC=EF B.AB=DE C.AC=DE D.AC=DF
3.如图2,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠AEC等于( )
A.60° B.50° C.45° D.30°
4.如图,AB=CD,AD=BC.求证:AD∥BC.
三、精练反馈
A组:
1.如图:△ABC和△ADE是等边三角形,证明:BD=CE。
2.如图,海岸上有、两个观测点,点在点的正东方,海岛在观测点的正北方,海岛在观测点的正北方,从观测点看海岛、的视角与从观测点看海岛、的视角相等。那么海岛、到观测点、所在海岸的距离相等。为什么?
B组:
在△ABC中,AC=BC,∠ACB=90°,直线经过点,且于,于。(1)当直线绕点旋转到图1的位置时,求证:
①≌;②;
(2)当直线绕点旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由。
【答案】
巩固训练
1.①DB=DC SAS ②∠B=∠C SSS
2.∠DBE AC
3.CO=DO
4.15
5.证明:(1)∵FB=CE ∴BF+FC=CE+FC ∴BC=EF ∵AC∥FD ∴∠ACB=∠DFE
在△ABC和△DEF中
∴△ABC≌△DEF(SAS)
∴AB=DE
(2)∵△ABC≌△DEF
∴∠B=∠E
∴AB∥DE
错题再现
1.C 2.C 3.A
4.证明:连接AC
在△ABC和△CDB中
∴△ABC≌△CDB(SSS) ∴ ∴AD∥BC
精练反馈
1.证明:
∵△ABC和△ADE是等边三角形
∴AB=AC AD=AE ∠BAC=∠DAE=60°
∴∠BAC-∠DAC=∠DAE-∠DAC
∴∠BAD=∠EAC
在△ABD和△EAC中
∴△ABD≌△EAC(SAS)
∴BD=CE
2.答:AC=BD
由题可知:
∠CAB=∠DBA ==90°
∴-∠CAB=-∠DBA
在△ABC和△DBA中
∴△ABC≌△DBA(ASA)
∴AC=BD
3.证明:
(1)①∵∠ACB=90°∴∠ACD+∠BCE=90°
∵ ∴∠DAC+∠DCA=90°∠ADC=90° ∴∠DAC=∠ECB
∵ ∴∠BEC=90°=∠ADC
在△ADC和△BCE中
∴△ADC≌△BCE(AAS)
②∵△ADC≌△BCE
∴DC=BE AD=EC
∴DE=DC+CE
∴DE=AD+BE
(2)答:不成立 DE=AD-BE
∵∠ACB=90° ∴∠ACD+∠BCE=90°
∵
∴∠DAC+∠DCA=90°∠ADC=90° ∴∠DAC=∠ECB
∵ ∴∠BEC=90°=∠ADC
在△ADC和△BCE中
∴△ADC≌△BCE(AAS)
∴DC=BE AD=EC
∵DE=CE-CD
∴DE=AD-BE
6 / 6
