2023-2024学年山东省济南市高新区七年级(上)期中数学试卷(PDF版含解析)
文档属性
| 名称 | 2023-2024学年山东省济南市高新区七年级(上)期中数学试卷(PDF版含解析) |  | |
| 格式 | |||
| 文件大小 | 722.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-12 10:29:23 | ||
图片预览




文档简介
2023-2024 学年山东省济南市高新区七年级(上)期中数学试卷
一、选择题(本大题共 12 个小题,每小题 4 分,共 48 分.在每小题给出的四个选项中,
只有一项是符合题目要求的.)
1.(4分)我国古代《九章算术)中注有“今两算得失相反,要令正负以名之”.意思是今
有两数若其意义相反,则分别叫做正数与负数,如果向北走 5步记作+5步,那么向南走
7步记作( )
A.+7步 B.﹣7步 C.+12步 D.﹣2步
2.(4分)用一个平面去截一个几何体,截面不可能是圆的几何体的是( )
A. B. C. D.
3.(4分)2023年歌曲《罗刹海市》席卷全球,据统计截止八月中旬,播放量突破惊人的
358亿,数字 35800000000用科学记数法表示为( )
A.358×108 B.3.58×109 C.3.58×1010 D.35.8×109
4.(4分)下列用字母表示数的式子中,符合书写要求的有( )
﹣2x2y,2×(a+b),a÷b,ab﹣2, , .
A.1个 B.2个 C.3个 D.4个
5.(4分)下列运算正确的是( )
A.﹣2﹣1=﹣1 B.﹣14=1
C. D.
6.(4 分)在下列各数﹣(+5)、﹣12、 、 、(﹣1)2023、﹣|﹣3|中,负数有
( )
A.2个 B.3个 C.4个 D.5个
7.(4分)某地一周前四天每天的最高气温与最低气温如表,则这四天中温差最大的是( )
星期 一 二 三 四
最高气温 10℃ 12℃ 11℃ 9℃
最低气温 3℃ 0℃ ﹣2℃ ﹣3℃
A.星期一 B.星期二 C.星期三 D.星期四
8.(4分)如图,是一个正方体的表面展开图,原正方体中与“学”字所在的面相对的面上
标的字是( )
A.心 B.素 C.养 D.数
9.(4分)下列说法正确的是( )
A.﹣ xy2的次数是 2
B. 是单项式
C.2a2﹣3abc﹣1是三次三项式
D.﹣2πab2的系数是﹣2
10.(4分)有理数 a,b,c、在数轴上的对应点的位置如图所示,有如下四个结论:①|a|
>3;②ab>0;③b+c>0;④b﹣a<0.上述结论中,所有正确结论的序号是( )
A.①② B.②③ C.②④ D.③④
11.(4 分)一个几何体的主视图和俯视图如图所示,若这个几何体最多由 a个小正方体组
成,最少由 b个小正方体组成,则 a+b等于( )
A.10 B.11 C.12
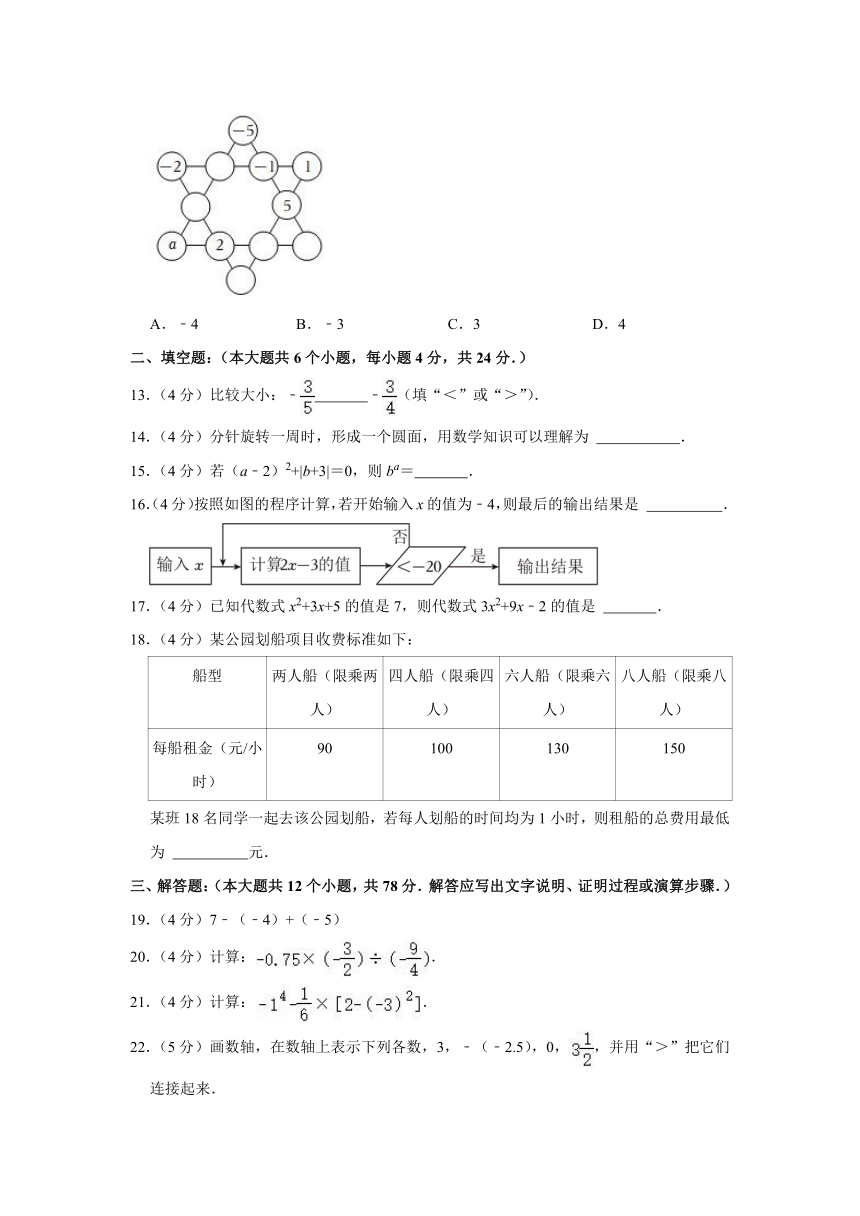
12.(4 分)如图,在探究“幻方”、“幻圆”的活动课上,学生们感悟到我国传统数学文化
的魅力.一个小组尝试将数字﹣5,﹣4,﹣3,﹣2,﹣1,0,1,2,3,4,5,6 这 12
个数填入“六角幻星”图中,使 6条边上四个数之和都相等,部分数字已填入圆圈中,
则 a的值为( )
A.﹣4 B.﹣3 C.3 D.4
二、填空题:(本大题共 6 个小题,每小题 4 分,共 24 分.)
13.(4分)比较大小:﹣ ﹣ (填“<”或“>”).
14.(4分)分针旋转一周时,形成一个圆面,用数学知识可以理解为 .
15.(4分)若(a﹣2)2+|b+3|=0,则 ba= .
16.(4分)按照如图的程序计算,若开始输入 x的值为﹣4,则最后的输出结果是 .
17.(4分)已知代数式 x2+3x+5的值是 7,则代数式 3x2+9x﹣2的值是 .
18.(4分)某公园划船项目收费标准如下:
船型 两人船(限乘两 四人船(限乘四 六人船(限乘六 八人船(限乘八
人) 人) 人) 人)
每船租金(元/小 90 100 130 150
时)
某班 18名同学一起去该公园划船,若每人划船的时间均为 1小时,则租船的总费用最低
为 元.
三、解答题:(本大题共 12 个小题,共 78 分.解答应写出文字说明、证明过程或演算步骤.)
19.(4分)7﹣(﹣4)+(﹣5)
20.(4分)计算: .
21.(4分)计算: .
22.(5分)画数轴,在数轴上表示下列各数,3,﹣(﹣2.5),0, ,并用“>”把它们
连接起来.
23.(5 分)如图,是由一些大小相同的小正方体组合成的简单几何体.根据要求完成下列
题目.
(1)请在下面方格纸中分别画出它的左视图和俯视图(画出的图需涂上阴影);
(2)图中共有 个小正方体.
24.(6分)把下列各数填入它所属的集合内:
5.2,0, , ,+(﹣4),﹣2 ,﹣(﹣3 ),﹣0.030030003…
(1)分数集合:{ …}
(2)非负整数集合:{ …}
(3)有理数集合:{ …}.
25.(6分)有 20箱石榴,以每箱 25kg为标准,超过或不足的千克数分别用正、负来表示,
记录如表:
与标准质量的差值(单位:kg) ﹣3 ﹣2 ﹣1.5 0 1 2.5
箱数 1 4 2 3 2 8
(1)20箱石榴中,最重的一箱比最轻的一箱多多少千克?
(2)与标准质量比较,20箱石榴总计超过或不足多少千克?
(3)若石榴每千克售价 8元,则售出这 20箱石榴总金额为多少元?
26.(6分)丁丁家要改造庭院,庭院中间空白部分是一个长 2m宽 1m的蓄水池,丁丁打算
在阴影部分种植草坪,对庭院进行绿化.
(1)写出用含 x、y的式子表示草坪面积;
(2)如果 x=8m,y=5m,绿化 1m2的平均费用为 20元,求绿化整个庭院的费用为多少?
27.(8分)某检修小组从 A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,
向西行驶为负,一天中七次行驶记录如下.(单位:km)
第一次 第二次 第三次 第四次 第五次 第六次 第七次
﹣4 +7 ﹣9 +8 +6 ﹣5 ﹣2
(1)求收工时,检修小组在 A地的何方向?距离 A地多远?
(2)在第几次纪录时距 A地最远?
(3)若汽车行驶每千米耗油 0.4升,问从 A地出发,检修结束后再回到 A地共耗油多少
升?
28.(8分)【情景创设】
是一组有规律的数,我们如何求这些连续数的和呢?
【探索活动】
(1)根据规律第 6个数是 , 是第 个数.
【阅读理解】
.
【实践应用】
根据上面获得的经验完成下面的计算:
(2) .
(3) .
29.(10分)某服装厂生产一种夹克和 T恤,夹克每件定价 200元,T恤每件定价 100元,
厂方在开展促销活动期间,向客户提供两种优惠方案:①买一件夹克送一件 T恤;②夹
克和 T恤都按定价的 80%付款.现某客户要到该服装厂购买夹克 30件,T恤 x件(x>
30).
( 1)若该客户按方案 ① 购买,夹克需付款 元, T 恤需付款
元(用含 x的式子表示);若该客户按方案②购买,夹克需付款 元,T恤需
付款 元(用含 x的式子表示);
(2)若 x=40,通过计算说明按方案①、方案②哪种方案购买较为合算?
(3)若两种优惠方案可同时使用,当 x=40时,你能给出一种更为省钱的购买方案吗?
试写出你的购买方案,并说明理由.
30.(12分)【概念学习】
规定:求若干个相同的有理数(均不等 0)的除法运算叫做除方,如 2÷2÷2,(﹣3)÷
(﹣3)÷(﹣3)÷(﹣3)等.类比有理数的乘方,我们把 2÷2÷2记作 2③,读作“2
的圈 3次方”,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)记作(﹣3)④,读作“﹣3 的圈 4
次方”.一般地,把 记作 a ,读作“a的圈 n次方”.
【初步探究】
(1)直接写出计算结果:(﹣3)④= .
【深入思考】
我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,那
有理数的除方运算也可以转化为乘方运算.
(2)试一试:仿照上面的算式,将下列运算结果直接写成幂的形式.
5⑤= ; = .
(3)将一个非零有理数 a的圈 n次方写成幂的形式:a = .
(4)利用(3)的结论计算: .
2023-2024 学年山东省济南市高新区七年级(上)期中数学试卷
参考答案与试题解析
一、选择题(本大题共 12 个小题,每小题 4 分,共 48 分.在每小题给出的四个选项中,
只有一项是符合题目要求的.)
1.(4分)我国古代《九章算术)中注有“今两算得失相反,要令正负以名之”.意思是今
有两数若其意义相反,则分别叫做正数与负数,如果向北走 5步记作+5步,那么向南走
7步记作( )
A.+7步 B.﹣7步 C.+12步 D.﹣2步
【分析】首先审清题意,明确“正”和“负”所表示的意义;再根据题意作答.
【解答】解:∵向北走 5步记作+5步,
∴向南走 7步记作﹣7步.
故选:B.
【点评】此题主要考查了正负数的意义,解题关键是理解“正”和“负”的相对性,明
确什么是一对具有相反意义的量.在一对具有相反意义的量中,先规定其中一个为正,
则另一个就用负表示.
2.(4分)用一个平面去截一个几何体,截面不可能是圆的几何体的是( )
A. B. C. D.
【分析】根据一个几何体有几个面,则截面最多为几边形,由于棱柱没有曲边,所以用
一个平面去截棱柱,截面不可能是圆.
【解答】解:用一个平面去截圆锥或圆柱,截面可能是圆,用一个平面去截球,截面是
圆,但用一个平面去截棱柱,截面不可能是圆.
故选:C.
【点评】本题考查了截一个几何体:用一个平面去截一个几何体,截出的面叫做截面.截
面的形状随截法的不同而改变,一般为多边形或圆,也可能是不规则图形,一般的截面
与几何体的几个面相交就得到几条交线,截面就是几边形,因此,若一个几何体有几个
面,则截面最多为几边形.
3.(4分)2023年歌曲《罗刹海市》席卷全球,据统计截止八月中旬,播放量突破惊人的
358亿,数字 35800000000用科学记数法表示为( )
A.358×108 B.3.58×109 C.3.58×1010 D.35.8×109
【分析】将一个数表示成 a×10n的形式,其中 1≤|a|<10,n为整数,这种记数方法叫做
科学记数法,据此即可求得答案.
【解答】解:35800000000=3.58×1010,
故选:C.
【点评】本题考查科学记数法表示较大的数,熟练掌握其定义是解题的关键.
4.(4分)下列用字母表示数的式子中,符合书写要求的有( )
﹣2x2y,2×(a+b),a÷b,ab﹣2, , .
A.1个 B.2个 C.3个 D.4个
【分析】根据代数式的书写要求分别进行判断即可.
【解答】解:用字母表示数的式子中,符合书写要求的有:﹣2x2y,ab﹣2, ,共有 3
个.
故选:C.
【点评】此题考查了列代数式,用到的知识点是代数式的书写要求:(1)在代数式中出
现的乘号,通常简写成“ ”或者省略不写;(2)数字与字母相乘时,数字要写在字母的
前面;(3)在代数式中出现的除法运算,一般按照分数的写法来写.带分数要写成假分
数的形式.
5.(4分)下列运算正确的是( )
A.﹣2﹣1=﹣1 B.﹣14=1
C. D.
【分析】利用有理数的加减运算的法则,有理数的除法的法则,乘方对各项进行运算即
可.
【解答】解:A、﹣2﹣1=﹣3,故 A不符合题意;
B、﹣14=﹣1,故 B不符合题意;
C、 ,故 C不符合题意;
D、5÷(﹣ )=﹣10,故 D符合题意;
故选:D.
【点评】本题主要考查有理数的混合运算,解答的关键是对相应的运算法则的掌握.
6.(4 分)在下列各数﹣(+5)、﹣12、 、 、(﹣1)2023、﹣|﹣3|中,负数有
( )
A.2个 B.3个 C.4个 D.5个
【分析】根据相反数、有理数的乘方、绝对值、负数的定义解决此题.
【解答】解:﹣(+5)=﹣5,﹣12=﹣1,(﹣ )2= ,﹣ =﹣ ,(﹣1)2023=﹣
1,﹣|﹣3|=﹣3.
故负数的个数为 5个.
故选:D.
【点评】本题主要考查相反数、有理数的乘方、绝对值、负数,熟练掌握相反数、有理
数的乘方、绝对值、负数的定义是解决本题的关键.
7.(4分)某地一周前四天每天的最高气温与最低气温如表,则这四天中温差最大的是( )
星期 一 二 三 四
最高气温 10℃ 12℃ 11℃ 9℃
最低气温 3℃ 0℃ ﹣2℃ ﹣3℃
A.星期一 B.星期二 C.星期三 D.星期四
【分析】用最高温度减去最低温度,结果最大的即为所求;
【解答】解:星期一温差 10﹣3=7℃;
星期二温差 12﹣0=12℃;
星期三温差 11﹣(﹣2)=13℃;
星期四温差 9﹣(﹣3)=12℃;
故选:C.
【点评】本题考查有理数的减法;能够理解题意,准确计算有理数减法是解题的关键.
8.(4分)如图,是一个正方体的表面展开图,原正方体中与“学”字所在的面相对的面上
标的字是( )
A.心 B.素 C.养 D.数
【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
则原正方体中与“学”字所在的面相对的面上标的字是心.
故选:A.
【点评】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对
面入手,分析及解答问题.
9.(4分)下列说法正确的是( )
A.﹣ xy2的次数是 2
B. 是单项式
C.2a2﹣3abc﹣1是三次三项式
D.﹣2πab2的系数是﹣2
【分析】单项式的系数是除去字母的数字,次数是所有字母的指数和,多项式项数所含
的单项式的个数,次数是最高次幂的指数.
【解答】解:A:﹣ xy2的次数是 3,故 A错;
B: 是分式,故 B错;
C:2a2﹣3abc﹣1是三次三项式,故 C正确;
D:﹣2πab2的系数是﹣2π,故 D错.
故选:C.
【点评】本题考查的是单项式和多项式的系数次数指数,解题的关键是熟记定义.
10.(4分)有理数 a,b,c、在数轴上的对应点的位置如图所示,有如下四个结论:①|a|
>3;②ab>0;③b+c>0;④b﹣a<0.上述结论中,所有正确结论的序号是( )
A.①② B.②③ C.②④ D.③④
【分析】根据绝对值的定义判断①;根据有理数的乘法法则判断②;根据有理数的加法
法则判断③;根据有理数的减法法则判断④.
【解答】解:∵﹣3<a<﹣2,
∴|a|<3,故①不符合题意;
∵a<0,b<0,
∴ab>0,故②符合题意;
∵b<0,c>0,|b|<|c|,
∴b+c>0,故③符合题意;
∵b>a,
∴b﹣a>0,故④不符合题意;
故选:B.
【点评】本题考查了绝对值,数轴,有理数的加、减、乘法法则,掌握在数轴上,一个
数表示的点到原点的距离是这个数的绝对值是解题的关键.
11.(4 分)一个几何体的主视图和俯视图如图所示,若这个几何体最多由 a个小正方体组
成,最少由 b个小正方体组成,则 a+b等于( )
A.10 B.11 C.12
【分析】易得这个几何体共有 2层,由俯视图可得第一层立方体的个数,由主视图可得
第二层立方体的可能的个数,相加即可.
【解答】解:结合主视图和俯视图可知,左边后排最多有 3个,左边前排最多有 3个,
右边只有一层,且只有 1个,
所以图中的小正方体最多 7块,
结合主视图和俯视图可知,左边后排最少有 1个,左边前排最多有 3个,右边只有一层,
且只有 1个,
所以图中的小正方体最少 5块,
a+b=12,
故选:C.
【点评】本题考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能
力方面的考查.
12.(4 分)如图,在探究“幻方”、“幻圆”的活动课上,学生们感悟到我国传统数学文化
的魅力.一个小组尝试将数字﹣5,﹣4,﹣3,﹣2,﹣1,0,1,2,3,4,5,6 这 12
个数填入“六角幻星”图中,使 6条边上四个数之和都相等,部分数字已填入圆圈中,
则 a的值为( )
A.﹣4 B.﹣3 C.3 D.4
【分析】根据将数字﹣5,﹣4,﹣3,﹣2,﹣1,0,1,2,3,4,5,6这 12个数填入“六
角幻星”图中,使 6条边上四个数之和都相等,可得 ,再观察
“六角幻星”图可知﹣a+3与﹣a﹣3相差 6,只有﹣3,3或 0,6满足,依此即可求解.
【解答】解:设右下边为 x,由满足 6 条边上四个数之和都相等,他们的和为 x﹣1,如
图所示:
观察图形还有﹣4,﹣3,0,3,4,6 五个数字,观察“六角幻星”图可知﹣a+3 与﹣a
﹣3相差 6,只有﹣3,3或 0,6满足,
则﹣a﹣3=﹣3或﹣a﹣3=0,
解得 a=0或 a=﹣3,
当 a=0时,x﹣(x+a﹣4)=4,x或 x+a﹣4又有 1个为 0(不合题意舍去),
当 a=﹣3时,符合题意.
故选:B.
【点评】本题考查了一元一次方程的应用,关键是用字母表示出﹣4,﹣3,0,3,4,6
五个数字,难度较大.
二、填空题:(本大题共 6 个小题,每小题 4 分,共 24 分.)
13.(4分)比较大小:﹣ > ﹣ (填“<”或“>”).
【分析】根据两负数比较大小绝对值大的反而小,可得答案.
【解答】解:|﹣ |= ,|﹣ |= ,
﹣ ,
故答案为:>.
【点评】本题考查了有理数比较大小,两负数比较大小绝对值大的反而小.
14.(4分)分针旋转一周时,形成一个圆面,用数学知识可以理解为 线动成面 .
【分析】根据几何体点、线、面、体之间的关系进行作答即可.
【解答】解:分针旋转一周时,形成一个圆面,用数学知识可以理解为:线动成面;
故答案为:线动成面.
【点评】本题考查几何体点、线、面、体之间的关系.熟练掌握点动成线,线动成面,
面动成体是解题的关键.
15.(4分)若(a﹣2)2+|b+3|=0,则 ba= 9 .
【分析】根据非负数的性质可求出 a、b的值,再将它们代入 ba中求解即可.
【解答】解:∵(a﹣2)2+|b+3|=0,
∴a﹣2=0,a=2;
b+3=0,b=﹣3;
则 ba=(﹣3)2=9.
故答案为:9.
【点评】本题考查了非负数的性质:有限个非负数的和为零,那么每一个加数也必为零.
16.(4 分)按照如图的程序计算,若开始输入 x的值为﹣4,则最后的输出结果是 ﹣
25 .
【分析】将 x的值代入进行计算后与﹣20进行比较即可.
【解答】解:当 x=﹣4时,2x﹣3=﹣11>﹣20,
当 x=﹣11时,2x﹣3=﹣25<﹣20,
则输出的结果为﹣25.
故答案为:﹣25.
【点评】本题考查了求代数式的值,能理解题意是解此题的关键.
17.(4分)已知代数式 x2+3x+5的值是 7,则代数式 3x2+9x﹣2的值是 4 .
【分析】根据题意求出 x2+3x的值,原式前两项提取 3变形后,将 x2+3x的值代入计算即
可求出值.
【解答】解:∵x2+3x+5=7,即 x2+3x=2,
∴原式=3(x2+3x)﹣2
=3×2﹣2
=6﹣2
=4.
故答案为:4.
【点评】本题考查了代数式求值,掌握整体代入思想和运算法则是关键.
18.(4分)某公园划船项目收费标准如下:
船型 两人船(限乘两 四人船(限乘四 六人船(限乘六 八人船(限乘八
人) 人) 人) 人)
每船租金(元/小 90 100 130 150
时)
某班 18名同学一起去该公园划船,若每人划船的时间均为 1小时,则租船的总费用最低
为 380 元.
【分析】分情况,列表格计算,即可得出结论.
【 解 答 】 解 : 如 图 , 由 题 意 列 表 得 ,
所以,费用最少为 380元,
故答案为:380.
【点评】此题主要考查了有理数的运算,用分类讨论的思想解决问题是解本题的关键.
三、解答题:(本大题共 12 个小题,共 78 分.解答应写出文字说明、证明过程或演算步骤.)
19.(4分)7﹣(﹣4)+(﹣5)
【分析】利用有理数的加减混合运算法则计算即可.
【解答】解:7﹣(﹣4)+(﹣5)
=7+4﹣5
=11﹣5
=6.
【点评】本题考查的是有理数的混合运算,掌握有理数的加减混合运算法则是解题的关
键.
20.(4分)计算: .
【分析】根据有理数的乘除法法则进行计算即可.
【解答】解:原式=﹣ × ×
=﹣ ×
=﹣ .
【点评】本题考查有理数的乘除法,掌握有理数的乘除法法则是解题的关键.
21.(4分)计算: .
【分析】根据有理数的混合运算的顺序计算.
【解答】解:
=﹣1﹣ ×(2﹣9)
=﹣1﹣ ×(﹣7)
=﹣1+
= .
【点评】本题考查了有理数的混合运算,解题的关键是掌握有理数混合运算的顺序.
22.(5分)画数轴,在数轴上表示下列各数,3,﹣(﹣2.5),0, ,并用“>”把它们
连接起来.
【分析】先化简﹣(﹣2.5),然后把各数表示在数轴上,再根据数轴上右边的数总比左边
的数大得出比较结果.
【解答】解:﹣(﹣2.5)=2.5,
如图所示:
用“>”连接为: .
【点评】本题考查了数轴,正负数,相反数,有理数的大小比较,熟知数轴的性质及有
理数的大小比较方法是解题的关键.
23.(5 分)如图,是由一些大小相同的小正方体组合成的简单几何体.根据要求完成下列
题目.
(1)请在下面方格纸中分别画出它的左视图和俯视图(画出的图需涂上阴影);
(2)图中共有 9 个小正方体.
【分析】(1)直接利用左视图以及俯视图的观察角度分析得出答案;
(2)结合几何体的形状得出答案.
【解答】解:(1)如图所示:
;
(2)图中共有 9个小正方体.
故答案为:9.
【点评】此题主要考查了简单几何体的三视图,正确注意观察角度是解题关键.
24.(6分)把下列各数填入它所属的集合内:
5.2,0, , ,+(﹣4),﹣2 ,﹣(﹣3 ),﹣0.030030003…
(1)分数集合:{ 5.2, ,﹣2 , …}
(2)非负整数集合:{ 0,﹣(﹣3) …}
(3)有理数集合:{ 5.2,0, ,+(﹣4),﹣2 ,﹣(﹣3) …}.
【分析】根据有理数的分类方法即可得到结果.
【解答】解:(1)分数集合:{ 5.2, ,﹣2 ,…};
(2)非负整数集合:{ 0,﹣(﹣3)…};
(3)有理数集合:{5.2,0, ,+(﹣4),﹣2 ,﹣(﹣3 )…}.
故答案为:5.2, ,﹣2 ;0,﹣(﹣3);5.2,0, ,+(﹣4),﹣2 ,﹣(﹣3 ).
【点评】此题考查了有理数,熟练掌握有理数的分类方法是解本题的关键.
25.(6分)有 20箱石榴,以每箱 25kg为标准,超过或不足的千克数分别用正、负来表示,
记录如表:
与标准质量的差值(单位:kg) ﹣3 ﹣2 ﹣1.5 0 1 2.5
箱数 1 4 2 3 2 8
(1)20箱石榴中,最重的一箱比最轻的一箱多多少千克?
(2)与标准质量比较,20箱石榴总计超过或不足多少千克?
(3)若石榴每千克售价 8元,则售出这 20箱石榴总金额为多少元?
【分析】(1)根据最大数减最小数,可得答案;
(2)根据有理数的加法,可得标准的重量,根据有理数的大小比较,可得答案;
(3)根据有理数的加法,可得总重量,根据单价乘以数量,可得答案.
【解答】解:(1)最重的一箱比最轻的一箱多重 2.5﹣(﹣3)=2.5+3=5.5(千克),
答:20箱石榴中,最重的一箱比最轻的一箱多重 5.5千克.
(2)﹣3×1+(﹣2)×4+(﹣1.5)×2+0×3+1×2+2.5×8=8(千克),
答:20箱石榴总计超过 8千克.
(3)(25×20+8)×8
=508×8
=4064(元),
答:售出这 20箱石榴可赚 4064元.
【点评】本题考查了正数和负数以及有理数的混合运算,正确列出算式并掌握相关运算
法则是解答本题的关键.
26.(6分)丁丁家要改造庭院,庭院中间空白部分是一个长 2m宽 1m的蓄水池,丁丁打算
在阴影部分种植草坪,对庭院进行绿化.
(1)写出用含 x、y的式子表示草坪面积;
(2)如果 x=8m,y=5m,绿化 1m2的平均费用为 20元,求绿化整个庭院的费用为多少?
【分析】(1)根据长方形面积公式可用含 x、y的式子表示草坪面积;
(2)将 x=8m,y=5m代入计算可求草坪面积,再乘 20可求绿化整个庭院的费用.
【解答】解:(1)草坪面积为 xy﹣2×1=(xy﹣2 )平方米;
(2)(8×5﹣2)×20
=(40﹣2)×20
=38×20
=760(元).
答:绿化整个庭院的费用为 760元.
【点评】考查了列代数式,能根据图形和题意列出算式是解此题的关键.
27.(8分)某检修小组从 A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,
向西行驶为负,一天中七次行驶记录如下.(单位:km)
第一次 第二次 第三次 第四次 第五次 第六次 第七次
﹣4 +7 ﹣9 +8 +6 ﹣5 ﹣2
(1)求收工时,检修小组在 A地的何方向?距离 A地多远?
(2)在第几次纪录时距 A地最远?
(3)若汽车行驶每千米耗油 0.4升,问从 A地出发,检修结束后再回到 A地共耗油多少
升?
【分析】(1)把所有行驶记录相加,再根据正数和负数的意义解答;
(2)分别写出各次记录时距离 A地的距离,然后判断即可;
(3)把所有行驶记录的绝对值相加,再乘以 0.4计算即可得解.
【解答】解:(1)﹣4+7﹣9+8+6﹣5﹣2=1
答:在 A地的东面 1km处
(2)第一次距 A地|﹣4|=4千米;
第二次:|﹣4+7|=3千米;
第三次:|﹣4+7﹣9|=6千米;
第四次:|﹣4+7﹣9+8|=2千米;
第五次:|﹣4+7﹣9+8+6|=8千米;
第六次:|﹣4+7﹣9+8+6﹣5|=3千米;
第七次:|﹣4+7﹣9+8+6﹣5﹣2|=1千米
第 5次记录是离 A地最远
(3)从出发到收工汽车行驶的总路程:|﹣4|+|+7|+|﹣9|+|+8|+|+6|+|﹣5|+|﹣2|+|1|=42(km)
从出发到收工共耗油:42×0.4=16.8(升).
答:从出发到收工共耗油 16.8.
【点评】此题分别考查了有理数的加法、正数和负数的意义及绝对值的定义,解题的关
键是熟练掌握有理数的加法法则及正负数的意义即可解决问题.
28.(8分)【情景创设】
是一组有规律的数,我们如何求这些连续数的和呢?
【探索活动】
(1)根据规律第 6个数是 , 是第 11 个数.
【阅读理解】
.
【实践应用】
根据上面获得的经验完成下面的计算:
(2) .
(3) .
【分析】(1)观察所给数列,发现它们的分子都是 1,分母是两个连续整数的积,据此可
解决问题.
(2)根据题中所给示例即可解决问题.
(3)将所给算式改写成分母为两个连续整数积的形式,再进行计算即可.
【解答】解:(1)由题知,
;
;
;
;
…,
所以第 n个数为: .
当 n=6时,
.
即第 6个数为 .
令 n(n+1)=132,
解得 n=11或﹣12,
又因为 n为正整数,
所以 n=11.
即 是第 11个数.
故答案为: ,11.
(2)原式=
=
=
= .
(3)原式=
=
=
=
=
=
=
= .
【点评】本题考查数字变化的规律,能根据题意发现第 n个数为 及巧妙利用裂
项相消法是解题的关键.
29.(10分)某服装厂生产一种夹克和 T恤,夹克每件定价 200元,T恤每件定价 100元,
厂方在开展促销活动期间,向客户提供两种优惠方案:①买一件夹克送一件 T恤;②夹
克和 T恤都按定价的 80%付款.现某客户要到该服装厂购买夹克 30件,T恤 x件(x>
30).
(1)若该客户按方案①购买,夹克需付款 6000 元,T恤需付款 100x﹣3000 元(用
含 x的式子表示);若该客户按方案②购买,夹克需付款 4800 元,T恤需付款 80x
元(用含 x的式子表示);
(2)若 x=40,通过计算说明按方案①、方案②哪种方案购买较为合算?
(3)若两种优惠方案可同时使用,当 x=40时,你能给出一种更为省钱的购买方案吗?
试写出你的购买方案,并说明理由.
【分析】(1)根据方案①和方案②列出代数式即可;
(2)把 x=40代入(1)中的代数式,求出后比较即可;
(3)先按方案①购买夹克 30件,再按方案②购买 T恤 10件更为省钱,通过计算说明
即可.
【解答】解:(1)若该客户按方案①购买,夹克需付款 200×30=6000(元),T恤需付
款 100(x﹣30)=(100x﹣3000)元;
若该客户按方案②购买,夹克需付款 200×30×80%=4800元,T恤需付款 100x×80%
=80x元,
故答案为:6000,100x﹣3000,4800;80x;
(2)当 x=40,按方案①购买所需费用=30×200+100(40﹣30)=6000+1000=7000
(元);
按方案②购买所需费用=30×200×80%+100×40×80%=4800+3200=8000(元),
所以按方案①购买较为合算;
(3)先按方案①购买夹克 30件,再按方案②购买 T恤 10件更为省钱,理由如下:
先按方案①购买夹克 30件所需费用=6000,按方案②购买 T恤 10件的费用=100×80%
×10=800,
所以总费用为 6000+800=6800(元),小于 7000元,
所以此种购买方案更为省钱.
【点评】本题考查了列代数式和求代数式的值,能正确根据题意列出代数式是解此题的
关键.
30.(12分)【概念学习】
规定:求若干个相同的有理数(均不等 0)的除法运算叫做除方,如 2÷2÷2,(﹣3)÷
(﹣3)÷(﹣3)÷(﹣3)等.类比有理数的乘方,我们把 2÷2÷2记作 2③,读作“2
的圈 3次方”,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)记作(﹣3)④,读作“﹣3 的圈 4
次方”.一般地,把 记作 a ,读作“a的圈 n次方”.
【初步探究】
(1)直接写出计算结果:(﹣3)④= .
【深入思考】
我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,那
有理数的除方运算也可以转化为乘方运算.
(2)试一试:仿照上面的算式,将下列运算结果直接写成幂的形式.
5⑤= ( )3 ; = 28 .
(3)将一个非零有理数 a的圈 n ﹣次方写成幂的形式:a = ( )n 2 .
(4)利用(3)的结论计算: .
【分析】(1)根据题意,可以求出所求式子的值;
(2)根据深入思考中的方法,可以求得所求数的值;
(3)根据题意,可以将一个非零有理数 a的圈 n次方写成幂的形式;
(4)根据(3)中的结果,可以求得所求式子的值.
【解答】解:(1)原式=(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)=3× × = ,
(2)5⑤=5÷5÷5÷5÷5÷5=5× × × =( )3;
=28;
故答案为: ,( )3,28;
(3 ﹣)一个非零有理数 a的圈 n次方写成幂的形式等于( )n 2,
﹣
故答案为:( )n 2;
(4)原式= .
【点评】本题考查有理数的混合运算,解答本题的关键是明确有理数混合运算的计算方法.
一、选择题(本大题共 12 个小题,每小题 4 分,共 48 分.在每小题给出的四个选项中,
只有一项是符合题目要求的.)
1.(4分)我国古代《九章算术)中注有“今两算得失相反,要令正负以名之”.意思是今
有两数若其意义相反,则分别叫做正数与负数,如果向北走 5步记作+5步,那么向南走
7步记作( )
A.+7步 B.﹣7步 C.+12步 D.﹣2步
2.(4分)用一个平面去截一个几何体,截面不可能是圆的几何体的是( )
A. B. C. D.
3.(4分)2023年歌曲《罗刹海市》席卷全球,据统计截止八月中旬,播放量突破惊人的
358亿,数字 35800000000用科学记数法表示为( )
A.358×108 B.3.58×109 C.3.58×1010 D.35.8×109
4.(4分)下列用字母表示数的式子中,符合书写要求的有( )
﹣2x2y,2×(a+b),a÷b,ab﹣2, , .
A.1个 B.2个 C.3个 D.4个
5.(4分)下列运算正确的是( )
A.﹣2﹣1=﹣1 B.﹣14=1
C. D.
6.(4 分)在下列各数﹣(+5)、﹣12、 、 、(﹣1)2023、﹣|﹣3|中,负数有
( )
A.2个 B.3个 C.4个 D.5个
7.(4分)某地一周前四天每天的最高气温与最低气温如表,则这四天中温差最大的是( )
星期 一 二 三 四
最高气温 10℃ 12℃ 11℃ 9℃
最低气温 3℃ 0℃ ﹣2℃ ﹣3℃
A.星期一 B.星期二 C.星期三 D.星期四
8.(4分)如图,是一个正方体的表面展开图,原正方体中与“学”字所在的面相对的面上
标的字是( )
A.心 B.素 C.养 D.数
9.(4分)下列说法正确的是( )
A.﹣ xy2的次数是 2
B. 是单项式
C.2a2﹣3abc﹣1是三次三项式
D.﹣2πab2的系数是﹣2
10.(4分)有理数 a,b,c、在数轴上的对应点的位置如图所示,有如下四个结论:①|a|
>3;②ab>0;③b+c>0;④b﹣a<0.上述结论中,所有正确结论的序号是( )
A.①② B.②③ C.②④ D.③④
11.(4 分)一个几何体的主视图和俯视图如图所示,若这个几何体最多由 a个小正方体组
成,最少由 b个小正方体组成,则 a+b等于( )
A.10 B.11 C.12
12.(4 分)如图,在探究“幻方”、“幻圆”的活动课上,学生们感悟到我国传统数学文化
的魅力.一个小组尝试将数字﹣5,﹣4,﹣3,﹣2,﹣1,0,1,2,3,4,5,6 这 12
个数填入“六角幻星”图中,使 6条边上四个数之和都相等,部分数字已填入圆圈中,
则 a的值为( )
A.﹣4 B.﹣3 C.3 D.4
二、填空题:(本大题共 6 个小题,每小题 4 分,共 24 分.)
13.(4分)比较大小:﹣ ﹣ (填“<”或“>”).
14.(4分)分针旋转一周时,形成一个圆面,用数学知识可以理解为 .
15.(4分)若(a﹣2)2+|b+3|=0,则 ba= .
16.(4分)按照如图的程序计算,若开始输入 x的值为﹣4,则最后的输出结果是 .
17.(4分)已知代数式 x2+3x+5的值是 7,则代数式 3x2+9x﹣2的值是 .
18.(4分)某公园划船项目收费标准如下:
船型 两人船(限乘两 四人船(限乘四 六人船(限乘六 八人船(限乘八
人) 人) 人) 人)
每船租金(元/小 90 100 130 150
时)
某班 18名同学一起去该公园划船,若每人划船的时间均为 1小时,则租船的总费用最低
为 元.
三、解答题:(本大题共 12 个小题,共 78 分.解答应写出文字说明、证明过程或演算步骤.)
19.(4分)7﹣(﹣4)+(﹣5)
20.(4分)计算: .
21.(4分)计算: .
22.(5分)画数轴,在数轴上表示下列各数,3,﹣(﹣2.5),0, ,并用“>”把它们
连接起来.
23.(5 分)如图,是由一些大小相同的小正方体组合成的简单几何体.根据要求完成下列
题目.
(1)请在下面方格纸中分别画出它的左视图和俯视图(画出的图需涂上阴影);
(2)图中共有 个小正方体.
24.(6分)把下列各数填入它所属的集合内:
5.2,0, , ,+(﹣4),﹣2 ,﹣(﹣3 ),﹣0.030030003…
(1)分数集合:{ …}
(2)非负整数集合:{ …}
(3)有理数集合:{ …}.
25.(6分)有 20箱石榴,以每箱 25kg为标准,超过或不足的千克数分别用正、负来表示,
记录如表:
与标准质量的差值(单位:kg) ﹣3 ﹣2 ﹣1.5 0 1 2.5
箱数 1 4 2 3 2 8
(1)20箱石榴中,最重的一箱比最轻的一箱多多少千克?
(2)与标准质量比较,20箱石榴总计超过或不足多少千克?
(3)若石榴每千克售价 8元,则售出这 20箱石榴总金额为多少元?
26.(6分)丁丁家要改造庭院,庭院中间空白部分是一个长 2m宽 1m的蓄水池,丁丁打算
在阴影部分种植草坪,对庭院进行绿化.
(1)写出用含 x、y的式子表示草坪面积;
(2)如果 x=8m,y=5m,绿化 1m2的平均费用为 20元,求绿化整个庭院的费用为多少?
27.(8分)某检修小组从 A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,
向西行驶为负,一天中七次行驶记录如下.(单位:km)
第一次 第二次 第三次 第四次 第五次 第六次 第七次
﹣4 +7 ﹣9 +8 +6 ﹣5 ﹣2
(1)求收工时,检修小组在 A地的何方向?距离 A地多远?
(2)在第几次纪录时距 A地最远?
(3)若汽车行驶每千米耗油 0.4升,问从 A地出发,检修结束后再回到 A地共耗油多少
升?
28.(8分)【情景创设】
是一组有规律的数,我们如何求这些连续数的和呢?
【探索活动】
(1)根据规律第 6个数是 , 是第 个数.
【阅读理解】
.
【实践应用】
根据上面获得的经验完成下面的计算:
(2) .
(3) .
29.(10分)某服装厂生产一种夹克和 T恤,夹克每件定价 200元,T恤每件定价 100元,
厂方在开展促销活动期间,向客户提供两种优惠方案:①买一件夹克送一件 T恤;②夹
克和 T恤都按定价的 80%付款.现某客户要到该服装厂购买夹克 30件,T恤 x件(x>
30).
( 1)若该客户按方案 ① 购买,夹克需付款 元, T 恤需付款
元(用含 x的式子表示);若该客户按方案②购买,夹克需付款 元,T恤需
付款 元(用含 x的式子表示);
(2)若 x=40,通过计算说明按方案①、方案②哪种方案购买较为合算?
(3)若两种优惠方案可同时使用,当 x=40时,你能给出一种更为省钱的购买方案吗?
试写出你的购买方案,并说明理由.
30.(12分)【概念学习】
规定:求若干个相同的有理数(均不等 0)的除法运算叫做除方,如 2÷2÷2,(﹣3)÷
(﹣3)÷(﹣3)÷(﹣3)等.类比有理数的乘方,我们把 2÷2÷2记作 2③,读作“2
的圈 3次方”,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)记作(﹣3)④,读作“﹣3 的圈 4
次方”.一般地,把 记作 a ,读作“a的圈 n次方”.
【初步探究】
(1)直接写出计算结果:(﹣3)④= .
【深入思考】
我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,那
有理数的除方运算也可以转化为乘方运算.
(2)试一试:仿照上面的算式,将下列运算结果直接写成幂的形式.
5⑤= ; = .
(3)将一个非零有理数 a的圈 n次方写成幂的形式:a = .
(4)利用(3)的结论计算: .
2023-2024 学年山东省济南市高新区七年级(上)期中数学试卷
参考答案与试题解析
一、选择题(本大题共 12 个小题,每小题 4 分,共 48 分.在每小题给出的四个选项中,
只有一项是符合题目要求的.)
1.(4分)我国古代《九章算术)中注有“今两算得失相反,要令正负以名之”.意思是今
有两数若其意义相反,则分别叫做正数与负数,如果向北走 5步记作+5步,那么向南走
7步记作( )
A.+7步 B.﹣7步 C.+12步 D.﹣2步
【分析】首先审清题意,明确“正”和“负”所表示的意义;再根据题意作答.
【解答】解:∵向北走 5步记作+5步,
∴向南走 7步记作﹣7步.
故选:B.
【点评】此题主要考查了正负数的意义,解题关键是理解“正”和“负”的相对性,明
确什么是一对具有相反意义的量.在一对具有相反意义的量中,先规定其中一个为正,
则另一个就用负表示.
2.(4分)用一个平面去截一个几何体,截面不可能是圆的几何体的是( )
A. B. C. D.
【分析】根据一个几何体有几个面,则截面最多为几边形,由于棱柱没有曲边,所以用
一个平面去截棱柱,截面不可能是圆.
【解答】解:用一个平面去截圆锥或圆柱,截面可能是圆,用一个平面去截球,截面是
圆,但用一个平面去截棱柱,截面不可能是圆.
故选:C.
【点评】本题考查了截一个几何体:用一个平面去截一个几何体,截出的面叫做截面.截
面的形状随截法的不同而改变,一般为多边形或圆,也可能是不规则图形,一般的截面
与几何体的几个面相交就得到几条交线,截面就是几边形,因此,若一个几何体有几个
面,则截面最多为几边形.
3.(4分)2023年歌曲《罗刹海市》席卷全球,据统计截止八月中旬,播放量突破惊人的
358亿,数字 35800000000用科学记数法表示为( )
A.358×108 B.3.58×109 C.3.58×1010 D.35.8×109
【分析】将一个数表示成 a×10n的形式,其中 1≤|a|<10,n为整数,这种记数方法叫做
科学记数法,据此即可求得答案.
【解答】解:35800000000=3.58×1010,
故选:C.
【点评】本题考查科学记数法表示较大的数,熟练掌握其定义是解题的关键.
4.(4分)下列用字母表示数的式子中,符合书写要求的有( )
﹣2x2y,2×(a+b),a÷b,ab﹣2, , .
A.1个 B.2个 C.3个 D.4个
【分析】根据代数式的书写要求分别进行判断即可.
【解答】解:用字母表示数的式子中,符合书写要求的有:﹣2x2y,ab﹣2, ,共有 3
个.
故选:C.
【点评】此题考查了列代数式,用到的知识点是代数式的书写要求:(1)在代数式中出
现的乘号,通常简写成“ ”或者省略不写;(2)数字与字母相乘时,数字要写在字母的
前面;(3)在代数式中出现的除法运算,一般按照分数的写法来写.带分数要写成假分
数的形式.
5.(4分)下列运算正确的是( )
A.﹣2﹣1=﹣1 B.﹣14=1
C. D.
【分析】利用有理数的加减运算的法则,有理数的除法的法则,乘方对各项进行运算即
可.
【解答】解:A、﹣2﹣1=﹣3,故 A不符合题意;
B、﹣14=﹣1,故 B不符合题意;
C、 ,故 C不符合题意;
D、5÷(﹣ )=﹣10,故 D符合题意;
故选:D.
【点评】本题主要考查有理数的混合运算,解答的关键是对相应的运算法则的掌握.
6.(4 分)在下列各数﹣(+5)、﹣12、 、 、(﹣1)2023、﹣|﹣3|中,负数有
( )
A.2个 B.3个 C.4个 D.5个
【分析】根据相反数、有理数的乘方、绝对值、负数的定义解决此题.
【解答】解:﹣(+5)=﹣5,﹣12=﹣1,(﹣ )2= ,﹣ =﹣ ,(﹣1)2023=﹣
1,﹣|﹣3|=﹣3.
故负数的个数为 5个.
故选:D.
【点评】本题主要考查相反数、有理数的乘方、绝对值、负数,熟练掌握相反数、有理
数的乘方、绝对值、负数的定义是解决本题的关键.
7.(4分)某地一周前四天每天的最高气温与最低气温如表,则这四天中温差最大的是( )
星期 一 二 三 四
最高气温 10℃ 12℃ 11℃ 9℃
最低气温 3℃ 0℃ ﹣2℃ ﹣3℃
A.星期一 B.星期二 C.星期三 D.星期四
【分析】用最高温度减去最低温度,结果最大的即为所求;
【解答】解:星期一温差 10﹣3=7℃;
星期二温差 12﹣0=12℃;
星期三温差 11﹣(﹣2)=13℃;
星期四温差 9﹣(﹣3)=12℃;
故选:C.
【点评】本题考查有理数的减法;能够理解题意,准确计算有理数减法是解题的关键.
8.(4分)如图,是一个正方体的表面展开图,原正方体中与“学”字所在的面相对的面上
标的字是( )
A.心 B.素 C.养 D.数
【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
则原正方体中与“学”字所在的面相对的面上标的字是心.
故选:A.
【点评】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对
面入手,分析及解答问题.
9.(4分)下列说法正确的是( )
A.﹣ xy2的次数是 2
B. 是单项式
C.2a2﹣3abc﹣1是三次三项式
D.﹣2πab2的系数是﹣2
【分析】单项式的系数是除去字母的数字,次数是所有字母的指数和,多项式项数所含
的单项式的个数,次数是最高次幂的指数.
【解答】解:A:﹣ xy2的次数是 3,故 A错;
B: 是分式,故 B错;
C:2a2﹣3abc﹣1是三次三项式,故 C正确;
D:﹣2πab2的系数是﹣2π,故 D错.
故选:C.
【点评】本题考查的是单项式和多项式的系数次数指数,解题的关键是熟记定义.
10.(4分)有理数 a,b,c、在数轴上的对应点的位置如图所示,有如下四个结论:①|a|
>3;②ab>0;③b+c>0;④b﹣a<0.上述结论中,所有正确结论的序号是( )
A.①② B.②③ C.②④ D.③④
【分析】根据绝对值的定义判断①;根据有理数的乘法法则判断②;根据有理数的加法
法则判断③;根据有理数的减法法则判断④.
【解答】解:∵﹣3<a<﹣2,
∴|a|<3,故①不符合题意;
∵a<0,b<0,
∴ab>0,故②符合题意;
∵b<0,c>0,|b|<|c|,
∴b+c>0,故③符合题意;
∵b>a,
∴b﹣a>0,故④不符合题意;
故选:B.
【点评】本题考查了绝对值,数轴,有理数的加、减、乘法法则,掌握在数轴上,一个
数表示的点到原点的距离是这个数的绝对值是解题的关键.
11.(4 分)一个几何体的主视图和俯视图如图所示,若这个几何体最多由 a个小正方体组
成,最少由 b个小正方体组成,则 a+b等于( )
A.10 B.11 C.12
【分析】易得这个几何体共有 2层,由俯视图可得第一层立方体的个数,由主视图可得
第二层立方体的可能的个数,相加即可.
【解答】解:结合主视图和俯视图可知,左边后排最多有 3个,左边前排最多有 3个,
右边只有一层,且只有 1个,
所以图中的小正方体最多 7块,
结合主视图和俯视图可知,左边后排最少有 1个,左边前排最多有 3个,右边只有一层,
且只有 1个,
所以图中的小正方体最少 5块,
a+b=12,
故选:C.
【点评】本题考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能
力方面的考查.
12.(4 分)如图,在探究“幻方”、“幻圆”的活动课上,学生们感悟到我国传统数学文化
的魅力.一个小组尝试将数字﹣5,﹣4,﹣3,﹣2,﹣1,0,1,2,3,4,5,6 这 12
个数填入“六角幻星”图中,使 6条边上四个数之和都相等,部分数字已填入圆圈中,
则 a的值为( )
A.﹣4 B.﹣3 C.3 D.4
【分析】根据将数字﹣5,﹣4,﹣3,﹣2,﹣1,0,1,2,3,4,5,6这 12个数填入“六
角幻星”图中,使 6条边上四个数之和都相等,可得 ,再观察
“六角幻星”图可知﹣a+3与﹣a﹣3相差 6,只有﹣3,3或 0,6满足,依此即可求解.
【解答】解:设右下边为 x,由满足 6 条边上四个数之和都相等,他们的和为 x﹣1,如
图所示:
观察图形还有﹣4,﹣3,0,3,4,6 五个数字,观察“六角幻星”图可知﹣a+3 与﹣a
﹣3相差 6,只有﹣3,3或 0,6满足,
则﹣a﹣3=﹣3或﹣a﹣3=0,
解得 a=0或 a=﹣3,
当 a=0时,x﹣(x+a﹣4)=4,x或 x+a﹣4又有 1个为 0(不合题意舍去),
当 a=﹣3时,符合题意.
故选:B.
【点评】本题考查了一元一次方程的应用,关键是用字母表示出﹣4,﹣3,0,3,4,6
五个数字,难度较大.
二、填空题:(本大题共 6 个小题,每小题 4 分,共 24 分.)
13.(4分)比较大小:﹣ > ﹣ (填“<”或“>”).
【分析】根据两负数比较大小绝对值大的反而小,可得答案.
【解答】解:|﹣ |= ,|﹣ |= ,
﹣ ,
故答案为:>.
【点评】本题考查了有理数比较大小,两负数比较大小绝对值大的反而小.
14.(4分)分针旋转一周时,形成一个圆面,用数学知识可以理解为 线动成面 .
【分析】根据几何体点、线、面、体之间的关系进行作答即可.
【解答】解:分针旋转一周时,形成一个圆面,用数学知识可以理解为:线动成面;
故答案为:线动成面.
【点评】本题考查几何体点、线、面、体之间的关系.熟练掌握点动成线,线动成面,
面动成体是解题的关键.
15.(4分)若(a﹣2)2+|b+3|=0,则 ba= 9 .
【分析】根据非负数的性质可求出 a、b的值,再将它们代入 ba中求解即可.
【解答】解:∵(a﹣2)2+|b+3|=0,
∴a﹣2=0,a=2;
b+3=0,b=﹣3;
则 ba=(﹣3)2=9.
故答案为:9.
【点评】本题考查了非负数的性质:有限个非负数的和为零,那么每一个加数也必为零.
16.(4 分)按照如图的程序计算,若开始输入 x的值为﹣4,则最后的输出结果是 ﹣
25 .
【分析】将 x的值代入进行计算后与﹣20进行比较即可.
【解答】解:当 x=﹣4时,2x﹣3=﹣11>﹣20,
当 x=﹣11时,2x﹣3=﹣25<﹣20,
则输出的结果为﹣25.
故答案为:﹣25.
【点评】本题考查了求代数式的值,能理解题意是解此题的关键.
17.(4分)已知代数式 x2+3x+5的值是 7,则代数式 3x2+9x﹣2的值是 4 .
【分析】根据题意求出 x2+3x的值,原式前两项提取 3变形后,将 x2+3x的值代入计算即
可求出值.
【解答】解:∵x2+3x+5=7,即 x2+3x=2,
∴原式=3(x2+3x)﹣2
=3×2﹣2
=6﹣2
=4.
故答案为:4.
【点评】本题考查了代数式求值,掌握整体代入思想和运算法则是关键.
18.(4分)某公园划船项目收费标准如下:
船型 两人船(限乘两 四人船(限乘四 六人船(限乘六 八人船(限乘八
人) 人) 人) 人)
每船租金(元/小 90 100 130 150
时)
某班 18名同学一起去该公园划船,若每人划船的时间均为 1小时,则租船的总费用最低
为 380 元.
【分析】分情况,列表格计算,即可得出结论.
【 解 答 】 解 : 如 图 , 由 题 意 列 表 得 ,
所以,费用最少为 380元,
故答案为:380.
【点评】此题主要考查了有理数的运算,用分类讨论的思想解决问题是解本题的关键.
三、解答题:(本大题共 12 个小题,共 78 分.解答应写出文字说明、证明过程或演算步骤.)
19.(4分)7﹣(﹣4)+(﹣5)
【分析】利用有理数的加减混合运算法则计算即可.
【解答】解:7﹣(﹣4)+(﹣5)
=7+4﹣5
=11﹣5
=6.
【点评】本题考查的是有理数的混合运算,掌握有理数的加减混合运算法则是解题的关
键.
20.(4分)计算: .
【分析】根据有理数的乘除法法则进行计算即可.
【解答】解:原式=﹣ × ×
=﹣ ×
=﹣ .
【点评】本题考查有理数的乘除法,掌握有理数的乘除法法则是解题的关键.
21.(4分)计算: .
【分析】根据有理数的混合运算的顺序计算.
【解答】解:
=﹣1﹣ ×(2﹣9)
=﹣1﹣ ×(﹣7)
=﹣1+
= .
【点评】本题考查了有理数的混合运算,解题的关键是掌握有理数混合运算的顺序.
22.(5分)画数轴,在数轴上表示下列各数,3,﹣(﹣2.5),0, ,并用“>”把它们
连接起来.
【分析】先化简﹣(﹣2.5),然后把各数表示在数轴上,再根据数轴上右边的数总比左边
的数大得出比较结果.
【解答】解:﹣(﹣2.5)=2.5,
如图所示:
用“>”连接为: .
【点评】本题考查了数轴,正负数,相反数,有理数的大小比较,熟知数轴的性质及有
理数的大小比较方法是解题的关键.
23.(5 分)如图,是由一些大小相同的小正方体组合成的简单几何体.根据要求完成下列
题目.
(1)请在下面方格纸中分别画出它的左视图和俯视图(画出的图需涂上阴影);
(2)图中共有 9 个小正方体.
【分析】(1)直接利用左视图以及俯视图的观察角度分析得出答案;
(2)结合几何体的形状得出答案.
【解答】解:(1)如图所示:
;
(2)图中共有 9个小正方体.
故答案为:9.
【点评】此题主要考查了简单几何体的三视图,正确注意观察角度是解题关键.
24.(6分)把下列各数填入它所属的集合内:
5.2,0, , ,+(﹣4),﹣2 ,﹣(﹣3 ),﹣0.030030003…
(1)分数集合:{ 5.2, ,﹣2 , …}
(2)非负整数集合:{ 0,﹣(﹣3) …}
(3)有理数集合:{ 5.2,0, ,+(﹣4),﹣2 ,﹣(﹣3) …}.
【分析】根据有理数的分类方法即可得到结果.
【解答】解:(1)分数集合:{ 5.2, ,﹣2 ,…};
(2)非负整数集合:{ 0,﹣(﹣3)…};
(3)有理数集合:{5.2,0, ,+(﹣4),﹣2 ,﹣(﹣3 )…}.
故答案为:5.2, ,﹣2 ;0,﹣(﹣3);5.2,0, ,+(﹣4),﹣2 ,﹣(﹣3 ).
【点评】此题考查了有理数,熟练掌握有理数的分类方法是解本题的关键.
25.(6分)有 20箱石榴,以每箱 25kg为标准,超过或不足的千克数分别用正、负来表示,
记录如表:
与标准质量的差值(单位:kg) ﹣3 ﹣2 ﹣1.5 0 1 2.5
箱数 1 4 2 3 2 8
(1)20箱石榴中,最重的一箱比最轻的一箱多多少千克?
(2)与标准质量比较,20箱石榴总计超过或不足多少千克?
(3)若石榴每千克售价 8元,则售出这 20箱石榴总金额为多少元?
【分析】(1)根据最大数减最小数,可得答案;
(2)根据有理数的加法,可得标准的重量,根据有理数的大小比较,可得答案;
(3)根据有理数的加法,可得总重量,根据单价乘以数量,可得答案.
【解答】解:(1)最重的一箱比最轻的一箱多重 2.5﹣(﹣3)=2.5+3=5.5(千克),
答:20箱石榴中,最重的一箱比最轻的一箱多重 5.5千克.
(2)﹣3×1+(﹣2)×4+(﹣1.5)×2+0×3+1×2+2.5×8=8(千克),
答:20箱石榴总计超过 8千克.
(3)(25×20+8)×8
=508×8
=4064(元),
答:售出这 20箱石榴可赚 4064元.
【点评】本题考查了正数和负数以及有理数的混合运算,正确列出算式并掌握相关运算
法则是解答本题的关键.
26.(6分)丁丁家要改造庭院,庭院中间空白部分是一个长 2m宽 1m的蓄水池,丁丁打算
在阴影部分种植草坪,对庭院进行绿化.
(1)写出用含 x、y的式子表示草坪面积;
(2)如果 x=8m,y=5m,绿化 1m2的平均费用为 20元,求绿化整个庭院的费用为多少?
【分析】(1)根据长方形面积公式可用含 x、y的式子表示草坪面积;
(2)将 x=8m,y=5m代入计算可求草坪面积,再乘 20可求绿化整个庭院的费用.
【解答】解:(1)草坪面积为 xy﹣2×1=(xy﹣2 )平方米;
(2)(8×5﹣2)×20
=(40﹣2)×20
=38×20
=760(元).
答:绿化整个庭院的费用为 760元.
【点评】考查了列代数式,能根据图形和题意列出算式是解此题的关键.
27.(8分)某检修小组从 A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,
向西行驶为负,一天中七次行驶记录如下.(单位:km)
第一次 第二次 第三次 第四次 第五次 第六次 第七次
﹣4 +7 ﹣9 +8 +6 ﹣5 ﹣2
(1)求收工时,检修小组在 A地的何方向?距离 A地多远?
(2)在第几次纪录时距 A地最远?
(3)若汽车行驶每千米耗油 0.4升,问从 A地出发,检修结束后再回到 A地共耗油多少
升?
【分析】(1)把所有行驶记录相加,再根据正数和负数的意义解答;
(2)分别写出各次记录时距离 A地的距离,然后判断即可;
(3)把所有行驶记录的绝对值相加,再乘以 0.4计算即可得解.
【解答】解:(1)﹣4+7﹣9+8+6﹣5﹣2=1
答:在 A地的东面 1km处
(2)第一次距 A地|﹣4|=4千米;
第二次:|﹣4+7|=3千米;
第三次:|﹣4+7﹣9|=6千米;
第四次:|﹣4+7﹣9+8|=2千米;
第五次:|﹣4+7﹣9+8+6|=8千米;
第六次:|﹣4+7﹣9+8+6﹣5|=3千米;
第七次:|﹣4+7﹣9+8+6﹣5﹣2|=1千米
第 5次记录是离 A地最远
(3)从出发到收工汽车行驶的总路程:|﹣4|+|+7|+|﹣9|+|+8|+|+6|+|﹣5|+|﹣2|+|1|=42(km)
从出发到收工共耗油:42×0.4=16.8(升).
答:从出发到收工共耗油 16.8.
【点评】此题分别考查了有理数的加法、正数和负数的意义及绝对值的定义,解题的关
键是熟练掌握有理数的加法法则及正负数的意义即可解决问题.
28.(8分)【情景创设】
是一组有规律的数,我们如何求这些连续数的和呢?
【探索活动】
(1)根据规律第 6个数是 , 是第 11 个数.
【阅读理解】
.
【实践应用】
根据上面获得的经验完成下面的计算:
(2) .
(3) .
【分析】(1)观察所给数列,发现它们的分子都是 1,分母是两个连续整数的积,据此可
解决问题.
(2)根据题中所给示例即可解决问题.
(3)将所给算式改写成分母为两个连续整数积的形式,再进行计算即可.
【解答】解:(1)由题知,
;
;
;
;
…,
所以第 n个数为: .
当 n=6时,
.
即第 6个数为 .
令 n(n+1)=132,
解得 n=11或﹣12,
又因为 n为正整数,
所以 n=11.
即 是第 11个数.
故答案为: ,11.
(2)原式=
=
=
= .
(3)原式=
=
=
=
=
=
=
= .
【点评】本题考查数字变化的规律,能根据题意发现第 n个数为 及巧妙利用裂
项相消法是解题的关键.
29.(10分)某服装厂生产一种夹克和 T恤,夹克每件定价 200元,T恤每件定价 100元,
厂方在开展促销活动期间,向客户提供两种优惠方案:①买一件夹克送一件 T恤;②夹
克和 T恤都按定价的 80%付款.现某客户要到该服装厂购买夹克 30件,T恤 x件(x>
30).
(1)若该客户按方案①购买,夹克需付款 6000 元,T恤需付款 100x﹣3000 元(用
含 x的式子表示);若该客户按方案②购买,夹克需付款 4800 元,T恤需付款 80x
元(用含 x的式子表示);
(2)若 x=40,通过计算说明按方案①、方案②哪种方案购买较为合算?
(3)若两种优惠方案可同时使用,当 x=40时,你能给出一种更为省钱的购买方案吗?
试写出你的购买方案,并说明理由.
【分析】(1)根据方案①和方案②列出代数式即可;
(2)把 x=40代入(1)中的代数式,求出后比较即可;
(3)先按方案①购买夹克 30件,再按方案②购买 T恤 10件更为省钱,通过计算说明
即可.
【解答】解:(1)若该客户按方案①购买,夹克需付款 200×30=6000(元),T恤需付
款 100(x﹣30)=(100x﹣3000)元;
若该客户按方案②购买,夹克需付款 200×30×80%=4800元,T恤需付款 100x×80%
=80x元,
故答案为:6000,100x﹣3000,4800;80x;
(2)当 x=40,按方案①购买所需费用=30×200+100(40﹣30)=6000+1000=7000
(元);
按方案②购买所需费用=30×200×80%+100×40×80%=4800+3200=8000(元),
所以按方案①购买较为合算;
(3)先按方案①购买夹克 30件,再按方案②购买 T恤 10件更为省钱,理由如下:
先按方案①购买夹克 30件所需费用=6000,按方案②购买 T恤 10件的费用=100×80%
×10=800,
所以总费用为 6000+800=6800(元),小于 7000元,
所以此种购买方案更为省钱.
【点评】本题考查了列代数式和求代数式的值,能正确根据题意列出代数式是解此题的
关键.
30.(12分)【概念学习】
规定:求若干个相同的有理数(均不等 0)的除法运算叫做除方,如 2÷2÷2,(﹣3)÷
(﹣3)÷(﹣3)÷(﹣3)等.类比有理数的乘方,我们把 2÷2÷2记作 2③,读作“2
的圈 3次方”,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)记作(﹣3)④,读作“﹣3 的圈 4
次方”.一般地,把 记作 a ,读作“a的圈 n次方”.
【初步探究】
(1)直接写出计算结果:(﹣3)④= .
【深入思考】
我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,那
有理数的除方运算也可以转化为乘方运算.
(2)试一试:仿照上面的算式,将下列运算结果直接写成幂的形式.
5⑤= ( )3 ; = 28 .
(3)将一个非零有理数 a的圈 n ﹣次方写成幂的形式:a = ( )n 2 .
(4)利用(3)的结论计算: .
【分析】(1)根据题意,可以求出所求式子的值;
(2)根据深入思考中的方法,可以求得所求数的值;
(3)根据题意,可以将一个非零有理数 a的圈 n次方写成幂的形式;
(4)根据(3)中的结果,可以求得所求式子的值.
【解答】解:(1)原式=(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)=3× × = ,
(2)5⑤=5÷5÷5÷5÷5÷5=5× × × =( )3;
=28;
故答案为: ,( )3,28;
(3 ﹣)一个非零有理数 a的圈 n次方写成幂的形式等于( )n 2,
﹣
故答案为:( )n 2;
(4)原式= .
【点评】本题考查有理数的混合运算,解答本题的关键是明确有理数混合运算的计算方法.
同课章节目录
