2023-2024学年山东省济南市历城区稼轩学校八年级(上)期中数学试卷(PDF版含解析)
文档属性
| 名称 | 2023-2024学年山东省济南市历城区稼轩学校八年级(上)期中数学试卷(PDF版含解析) |  | |
| 格式 | |||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-12 10:42:39 | ||
图片预览

文档简介
2023-2024 学年山东省济南市历城区稼轩学校八年级(上)期中
数学试卷
一.选择题(每小题 4 分,共 40 分)
1.(4分)以下各数﹣3, , ,π,1.9191191119…(每两个 9之间依次多一个 1),其
中无理数的个数是( )
A.1个 B.2个 C.3个 D.4个
2.(4分)平面直角坐标系中,与点 A(﹣2,3)关于 x轴对称的点的坐标为( )
A.(2,3) B.(﹣2,3) C.(﹣3,2) D.(﹣2,﹣3)
3.(4分)如图所示的数轴被墨迹污染了,则下列选项中可能被覆盖住的数是( )
A. B.﹣ C.﹣ D.﹣
4.(4分)已知 A(﹣ ,y1)、B(﹣ ,y2)、C(1,y3)是一次函数 y=﹣3x+b的图象上
三点,则 y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y1<y3 C.y3<y1<y2 D.y3<y2<y1
5.(4分)一次函数 y=kx和 y=﹣x+3的图象如图所示,则二元一次方程组 的解
是( )
A. B. C. D.
6.(4分)已知 是二元一次方程组 的解,则 a﹣b的值为( )
A.3 B.2 C.1 D.﹣1
7.(4分)一次函数 y1=mx+n与 y2=mnx(m、n为常数,且 mn≠0)在同一平面直角坐标
内的图象可能是( )
A. B.
C. D.
8.(4分)母亲节来临,小明去花店为妈妈准备节日礼物.已知康乃馨每支 2元,百合每支
3元.小明将 20元钱全部用于购买这两种花(两种花都买),小明的购买方案共有( )
A.2种 B.3种 C.4种 D.5种
9.(4分)“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如
图所示的“赵爽弦图”是由四个全等的直角三角形(如图 1)拼成的一个大正方形(如图
2).设直角三角形较长
直角边长为 a,较短直角边长为 b.若 ab=8,大正方形的面积为 25,则图 2中 EF的长
为( )
A.3 B.4 C. D.
10.(4分)如图,直线 y=2x﹣6与 x轴、y轴分别交于 A,B两点,C在 y轴的正半轴上,
D在直线 AB上,且 CB=10,CD=OD.若点 P为线段 AB上的一个动点,且 P关于 x
轴的对称点 Q总在△OCD内(不包括边界),则点 P的横坐标 m的取值范围为( )
A. B. C. D.
二.填空题(每小题 4 分,共 24 分)
11.(4分)10的算术平方根是 .
12.(4分)如图,在数轴上点 D表示的实数为 .
13.(4分)在平面直角坐标系中,点 P(m,3),点 Q(2﹣2m,m﹣3),且 PQ∥y轴,则
m= .
14.(4分)一支原长为 12cm的蜡烛,点燃后其剩余长度与燃烧时间之间的关系如下表:
燃烧时间/分 10 20 30 40 50 …
剩余长度/cm 11.2 10.4 9.6 8.8 8 …
则这支蜡烛最多可燃烧 分钟.
15.(4分)利用两块完全一样的长方体木块测量一张桌子的高度,首先按图①所示的方式
放置,图示距离为 110cm;再交换两木块的位置,按图②所示的方式放置,图示距离为
60cm,则桌子的高度等于 cm.
16.(4分)已知一次函数 y=ax﹣a+2(a为常数,且 a≠0).若当﹣1≤x≤4时,函数有最
大值 7,则 a的值为 .
三、解答题(共 9 个小题,共 86 分)
17.(8分)化简与求值:
(1) ;
(2) .
18.(10分)解方程组:
(1) ;
(2) .
19.(8分)△ABC在平面直角坐标系中的位置如图所示,A、B、C三点在格点上.
(1)作出△ABC关于 x轴对称的△A1B1C1,并写出点 C1的坐标;
(2)在 y轴上求作点 D,使得 AD+BD最小,请你直接写出 D点坐标;
(3)若点 P为 x轴上一动点,且满足△BCP的面积为 1,请你直接写出 P点坐标.
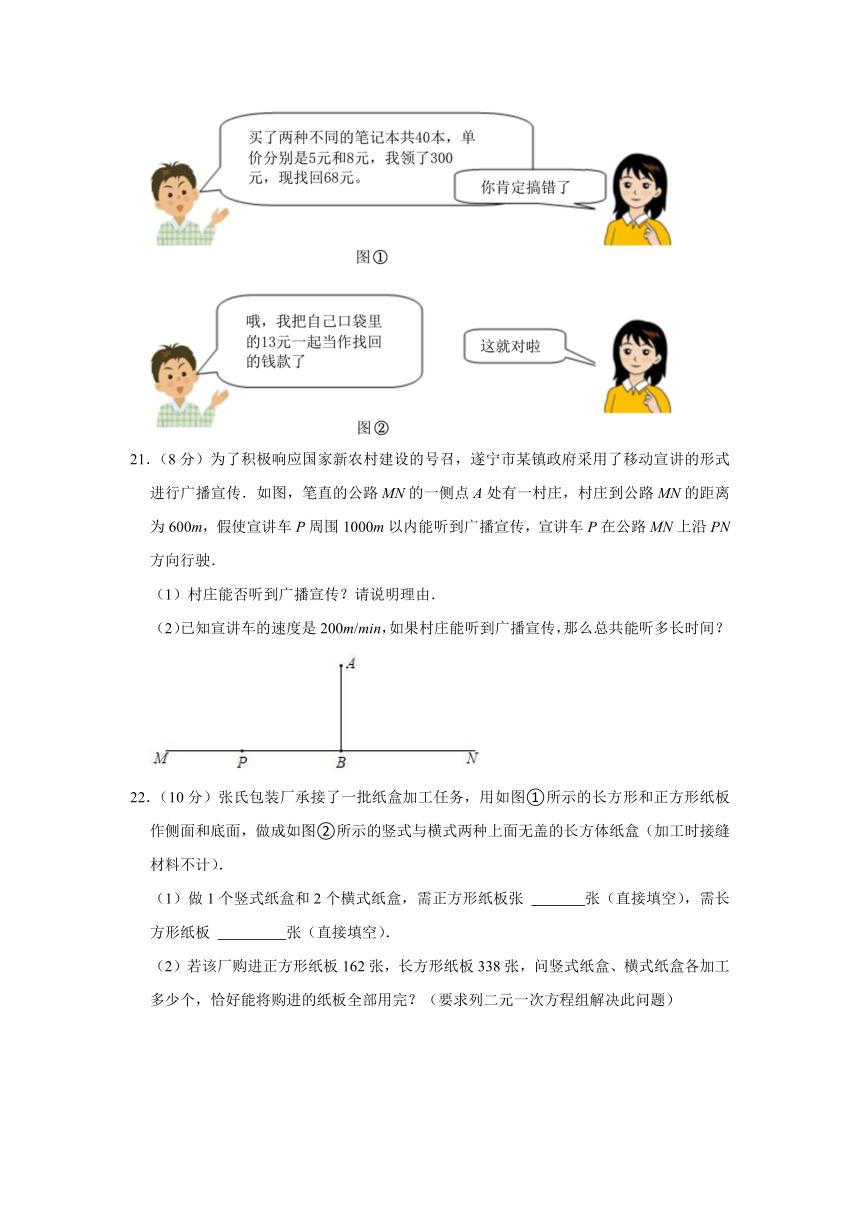
20.(8 分)某班级为表彰运动会表现优秀的同学,班主任老师安排小明和小红购买奖品,
图①,图 2是小明和小红购买奖品后的对话情境,根据信息解决问题,试计算两种笔记
本各买了多少本?
21.(8 分)为了积极响应国家新农村建设的号召,遂宁市某镇政府采用了移动宣讲的形式
进行广播宣传.如图,笔直的公路 MN的一侧点 A处有一村庄,村庄到公路 MN的距离
为 600m,假使宣讲车 P周围 1000m以内能听到广播宣传,宣讲车 P在公路 MN上沿 PN
方向行驶.
(1)村庄能否听到广播宣传?请说明理由.
(2)已知宣讲车的速度是 200m/min,如果村庄能听到广播宣传,那么总共能听多长时间?
22.(10分)张氏包装厂承接了一批纸盒加工任务,用如图①所示的长方形和正方形纸板
作侧面和底面,做成如图②所示的竖式与横式两种上面无盖的长方体纸盒(加工时接缝
材料不计).
(1)做 1个竖式纸盒和 2个横式纸盒,需正方形纸板张 张(直接填空),需长
方形纸板 张(直接填空).
(2)若该厂购进正方形纸板 162张,长方形纸板 338张,问竖式纸盒、横式纸盒各加工
多少个,恰好能将购进的纸板全部用完?(要求列二元一次方程组解决此问题)
23.(10分)小明在解决问题:已知 ,求 2a2﹣8a+1的值,他是这样分析与解答的:
∵ ,
∴ .
∴(a﹣2)2=3,即 a2﹣4a+4=3.
∴a2﹣4a=﹣1,
∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1.
请你根据小明的分析过程,解决如下问题:
(1)计算: = ;
(2)计算: + ;
(3)若 a= ,求 2a2﹣8a+1的值.
24.(12分)在 A、B两地之间有服务区 C,甲车由 A地驶往服务区 C,乙车由 B地驶往 A
地,两车同时出发,匀速行驶.如图是甲、乙两车分别距离服务区 C的路程 y1、y2(单
位:千米)与乙车行驶时间 x(单位:小时)之间的函数图象,结合图象信息,解答下列
问题:
(1)甲车的速度是 千米/时;
(2)求图象中线段 DF的函数解析式;
(3)当两车距服务区 C的路程之和是 360千米时,直接写出此时乙车的行驶时间.
25.(12分)如图 1,已知直线 l1:y=﹣x+5与 x轴交于点 A,与 y轴交于点 B,直线 l2与 y
轴交于点 C(0,﹣1),与直线 l1交于点 D(2,t).
(1)求直线 l2的解析式;
(2)如图 2,若点 P在直线 l1上,过点 P作 PQ∥y轴交 l2于点 Q,交 x轴于点 G,使 S
△PCG=2S△QCG,求此时 P点的坐标;
(3)将直线 l1:y=﹣x+5向左平移 10个单位得直线 l3交 x轴于点 E,点 F是点 C关于
原点的对称点.过点 F作直线 l4∥x轴.在直线 l4上是否存在动点 M,使得△MCE为等
腰三角形?若存在,请直接写出点 M的坐标;若不存在,请说明理由.
2023-2024 学年山东省济南市历城区稼轩学校八年级(上)期中
数学试卷
参考答案与试题解析
一.选择题(每小题 4 分,共 40 分)
1.(4分)以下各数﹣3, , ,π,1.9191191119…(每两个 9之间依次多一个 1),其
中无理数的个数是( )
A.1个 B.2个 C.3个 D.4个
【分析】根据无理数的定义:不能表示成两个整数之商的数即不循环的无限小数即可求
解.
【解答】解:﹣3是整数,不是无理数,
是无限不循环小数,是无理数,
是分数,不是无理数,
π是无限不循环小数,是无理数,
1.9191191119…(每两个 9之间依次多一个 1)是无限不循环小数,是无理数,
符合题意的有 3个,
故选:C.
【点评】本题主要考查了无理数,掌握无理数的定义是解题的关键.
2.(4分)平面直角坐标系中,与点 A(﹣2,3)关于 x轴对称的点的坐标为( )
A.(2,3) B.(﹣2,3) C.(﹣3,2) D.(﹣2,﹣3)
【分析】根据“关于 x轴对称的点,横坐标相同,纵坐标互为相反数”解答即可.
【解答】解:点 A(﹣2,3)关于 x轴对称的点的坐标为(﹣2,﹣3).
故选:D.
【点评】本题考查了关于 x轴、y轴对称的点的坐标,解决本题的关键是掌握好对称点的
坐标规律:(1)关于 x轴对称的点,横坐标相同,纵坐标互为相反数;(2)关于 y轴对
称的点,纵坐标相同,横坐标互为相反数.
3.(4分)如图所示的数轴被墨迹污染了,则下列选项中可能被覆盖住的数是( )
A. B.﹣ C.﹣ D.﹣
【分析】根据题意可知在﹣3与﹣2之间,据此判断,观察选项中的四个数哪一个在这个
范围内即可.
【解答】解:设被覆盖住的数是 x,
由图可知:﹣3<x<﹣2,
∵﹣ <﹣ ,即 <﹣3,不在此范围内,故 A错;
∵﹣ ≈﹣1.732>﹣2,不在此范围内,故 C错;
∵﹣ ≈﹣1.414>﹣2,不在此范围内,故 D错;
所以 B正确,
故选:B.
【点评】本题考查有理数的大小比较,是基础题.
4.(4分)已知 A(﹣ ,y1)、B(﹣ ,y2)、C(1,y3)是一次函数 y=﹣3x+b的图象上
三点,则 y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y1<y3 C.y3<y1<y2 D.y3<y2<y1
【分析】利用一次函数图象上点的坐标特征可求出 y1,y2,y3的值,比较后可得出结论.
【解答】解:∵A(﹣ ,y1)、B(﹣ ,y2)、C(1,y3)是一次函数 y=﹣3x+b的图象
上三点,
∴y1=1+b,y2= +b,y3=﹣3+b.
∵﹣3+b<1+b< +b,
∴y3<y1<y2.
故选:C.
【点评】本题考查了一次函数图象上点的坐标特征,利用一次函数图象上点的坐标特征,
求出 y1,y2,y3的值是解题的关键.
5.(4分)一次函数 y=kx和 y=﹣x+3的图象如图所示,则二元一次方程组 的解
是( )
A. B. C. D.
【分析】两个一次函数图象的交点坐标就是两函数组成的方程组的解.
【解答】解:∵一次函数 y=kx和 y=﹣x+3的图象交于点(1,2),
∴二元一次方程组 的解是 ,
故选:A.
【点评】此题主要考查了一次函数与二元一次方程组,掌握二元一次方程(组)与一次
函数的关系是解题的关键.
6.(4分)已知 是二元一次方程组 的解,则 a﹣b的值为( )
A.3 B.2 C.1 D.﹣1
【分析】把 x=2.y=1代入方程组 得出方程组 求出方程组的解即
可.
【解答】解:把 x=2.y=1代入方程组 得:
①+②得:4a=8,
解得:a=2,
把 a=2代入①得:4+b=7,
解得:b=3,
a﹣b=2﹣3=﹣1,
故选:D.
【点评】本题考查了二元一次方程组的解,解二元一次方程组的应用,解此题的关键是
能得出关于 a、b的方程组,难度适中.
7.(4分)一次函数 y1=mx+n与 y2=mnx(m、n为常数,且 mn≠0)在同一平面直角坐标
内的图象可能是( )
A. B.
C. D.
【分析】根据一次函数与正比例函数的性质对四个选项进行逐一分析即可.
【解答】解:A、由一次函数的图象可知,m<0,n>0,故 mn<0;由正比例函数的图
象可知 mn<0,两结论一致,故本选项符合题意;
B、由一次函数的图象可知,m<0,n>0,故 mn<0;由正比例函数的图象可知 mn>0,
两结论不一致,故本选项不符合题意;
C、由一次函数的图象可知,m>0,n>0,故 mn>0;由正比例函数的图象可知 mn<0,
两结论不一致,故本选项不符合题意;
D、由一次函数的图象可知,m>0,n<0,故 mn<0;由正比例函数的图象可知 mn>0,
两结论不一致,故本选项不符合题意.
故选:A.
【点评】此题主要考查了一次函数的图象性质,要掌握它的性质才能灵活解题.
一次函数 y=kx+b的图象有四种情况:
①当 k>0,b>0时,函数 y=kx+b的图象经过第一、二、三象限;
②当 k>0,b<0时,函数 y=kx+b的图象经过第一、三、四象限;
③当 k<0,b>0时,函数 y=kx+b的图象经过第一、二、四象限;
④当 k<0,b<0时,函数 y=kx+b的图象经过第二、三、四象限.
8.(4分)母亲节来临,小明去花店为妈妈准备节日礼物.已知康乃馨每支 2元,百合每支
3元.小明将 20元钱全部用于购买这两种花(两种花都买),小明的购买方案共有( )
A.2种 B.3种 C.4种 D.5种
【分析】设可以购买 x支康乃馨,y支百合,根据总价=单价×数量,即可得出关于 x,
y的二元一次方程,结合 x,y均为正整数即可得出小明有 3种购买方案.
【解答】解:设可以购买 x支康乃馨,y支百合,
依题意,得:2x+3y=20,
∴x=10﹣ y.
∵x,y均为正整数,
∴ 或 或 ,
∴小明有 3种购买方案.
故选:B.
【点评】本题考查了二元一次方程的应用,找准等量关系,正确列出二元一次方程是解
题的关键.
9.(4分)“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如
图所示的“赵爽弦图”是由四个全等的直角三角形(如图 1)拼成的一个大正方形(如图
2).设直角三角形较长
直角边长为 a,较短直角边长为 b.若 ab=8,大正方形的面积为 25,则图 2中 EF的长
为( )
A.3 B.4 C. D.
【分析】由图形 2可知,中间四边形的边长为(a﹣b)的小正方形,由大正方形的面积
由四个全等的直角三角形加中间小正方形的面积得出 =25,再结合 ab
=8即可得出(a﹣b)的值,再根据勾股定理即可求出 EF的长.
【解答】解:由图形 2可知,中间四边形的边长为(a﹣b)的小正方形,
∵大正方形的面积为 25,
∴AB2=25,
又∵大正方形的面积由四个全等的直角三角形加中间小正方形的面积,
∴ =25,
∴(a﹣b)2+2ab=25,
∴(a﹣b)2+2×8=25,
∴(a﹣b)=3(负值已舍),
即图 2中小正方形的边长为 3,
∴EF= =3 ,
故选:D.
【点评】本题考查了勾股定理的证明,勾股定理,正确得出大正方形的面积表示方法是
解题的关键.
10.(4分)如图,直线 y=2x﹣6与 x轴、y轴分别交于 A,B两点,C在 y轴的正半轴上,
D在直线 AB上,且 CB=10,CD=OD.若点 P为线段 AB上的一个动点,且 P关于 x
轴的对称点 Q总在△OCD内(不包括边界),则点 P的横坐标 m的取值范围为( )
A. B. C. D.
【分析】先求出 A(3,0)、B(0,﹣6),进而求出 C(0,4),再由 CD=OD可知点 D
在线段 OC的垂直平分线上,即在直线 y=2 上,则 D(4,2),利用待定系数法求出直
线 CD和直线 OD的解析式,根据关于 x轴对称的点横坐标相同及坐标互为相反数求出
点 Q的坐标,再根据点 Q在△OCD内,则当 x=m时,点 Q的纵坐标在直线 CD和直线
OD二者的函数值之间,由此建立不等式求解即可.
【解答】解:在 y=2x﹣6中,当 x=0时,y=2x﹣6=﹣6,当 y=2x﹣6=0时,x=3,
∴A(3,0),B(0,﹣6),
∵C在 y轴的正半轴上,CB=10,
∴C(0,4),
∵CD=OD.
∴点 D在线段 OC的垂直平分线上,即在直线 y=2上,
在 y=2x﹣6中,当 y=2x﹣6=2时,x=4,
∴D(4,2);
设直线 CD解析式为 y=kx+b,
,
∴
∴直线 CD解析式为 y=﹣ x+4.
同理可得直线 OD的解析式为 y= x,
∵点 P为线段 AB上的一个动点,且其横坐标为 m,
∴P(m,2m﹣6),
∵P、Q关于 x轴对称,
∴Q(m,6﹣2m),
∵点 Q总在△OCD内(不包括边界),
∴ m<6﹣2m<﹣ m+4.
解得 <m< .
故选:D.
【点评】本题主要考查了一次函数与几何综合,坐标与图形变化一轴对称,正确理解题
意得到点 Q在△OCD内,则当 x=m时,点 Q的纵坐标在直线 CD和直线 OD二者的函
数值之间是解题的关键.
二.填空题(每小题 4 分,共 24 分)
11.(4分)10的算术平方根是 .
【分析】根据算术平方根的定义进行解答即可.
【解答】解:10的算术平方根是 .
故答案为: .
【点评】本题主要考查了求一个数的算术平方根,解题的关键是熟练掌握算术平方根的
定义.
12.(4分)如图,在数轴上点 D表示的实数为 1﹣ .
【分析】根据勾股定理求出圆弧的半径,再根据点 D的位置可得答案.
【解答】解:∵AB=2﹣1=1,AC=2,
∴BC= = ,
∴点 D表示的数为 1﹣ ,
故答案为:1﹣ .
【点评】本题考查了实数与数轴,勾股定理的应用,体现了数形结合的数学思想,解题
时注意点 D在数轴的负半轴上.
13.(4分)在平面直角坐标系中,点 P(m,3),点 Q(2﹣2m,m﹣3),且 PQ∥y轴,则
m= .
【分析】根据平行于 y轴的直线上的点横坐标相同求出 m的值即可
【解答】解:∵P(m,3),点 Q(2﹣2m,m﹣3),且 PQ∥y轴,
∴m=2﹣2m,
解得: ,
故答案为: .
【点评】本题主要考查了坐标与图形,熟知平行于 y轴的直线上的点横坐标相同是解题
的关键.
14.(4分)一支原长为 12cm的蜡烛,点燃后其剩余长度与燃烧时间之间的关系如下表:
燃烧时间/分 10 20 30 40 50 …
剩余长度/cm 11.2 10.4 9.6 8.8 8 …
则这支蜡烛最多可燃烧 150 分钟.
【分析】设这支蜡烛剩余长度为 ycm,燃烧时间为 x分钟,根据蜡烛剩余长度与燃烧时
间的关系可知每燃烧 10分钟,蜡烛剩余长度减少 0.8cm,由此建立 y与 x之间的函数关
系式,再求出 y=0时的 x值即可.
【解答】解:设这支蜡烛剩余长度为 ycm,燃烧时间为 x分钟,由表可知,每燃烧 10分
钟,蜡烛剩余长度减少 0.8cm,
则 y=12﹣0.08x,
当 y=0时,12﹣0.08x=0,
解得 x=150,
所以这支蜡烛最多可燃烧 150分钟,
故答案为:150.
【点评】本题考查了一次函数的实际应用,正确求出函数关系式是解题关键.
15.(4分)利用两块完全一样的长方体木块测量一张桌子的高度,首先按图①所示的方式
放置,图示距离为 110cm;再交换两木块的位置,按图②所示的方式放置,图示距离为
60cm,则桌子的高度等于 85 cm.
【分析】根据“按图①所示的方式放置,图示距离为 110cm”和“图②所示的方式放置,
图示距离为 60cm”列方程组求解.
【解答】解:设桌子的高度为 xcm,长方体木块的长为 acm,宽为 bcm,
则: ,
①+②得:2x=170,
解得:x=85,
故答案为:85.
【点评】本题考查了三元一次方程组的应用,找到相等关系是解题的关键.
16.(4分)已知一次函数 y=ax﹣a+2(a为常数,且 a≠0).若当﹣1≤x≤4时,函数有最
大值 7,则 a的值为 或﹣ .
【分析】分类讨论:a>0 时,y随 x的增大而增大,所以当 x=2 时,y有最大值 2,然
后把 y=2代入函数关系式可计算出对应 a的值;a<0时,y随 x的增大而减小,所以当
x=﹣1时,y有最大值 2,然后把 x=﹣1代入函数关系式可计算对应 a的值.
【解答】解:①a>0时,y随 x的增大而增大,
则当 x=4时,y有最大值 7,把 x=4,y=7代入函数关系式得 7=4a﹣a+2,解得 a= ;
②a<0时,y随 x的增大而减小,
则当 x=﹣1时,y有最大值 7,把 x=﹣1代入函数关系式得 7=﹣a﹣a+2,解得 a=﹣ ,
所以 a= 或 a=﹣ ,
故答案为 或﹣ .
【点评】本题考查了一次函数的性质:k>0,y随 x的增大而增大,函数从左到右上升;
k<0,y随 x的增大而减小,函数从左到右下降.由于 y=kx+b与 y轴交于(0,b),当 b
>0时,(0,b)在 y轴的正半轴上,直线与 y轴交于正半轴;当 b<0 时,(0,b)在 y
轴的负半轴,直线与 y轴交于负半轴.
三、解答题(共 9 个小题,共 86 分)
17.(8分)化简与求值:
(1) ;
(2) .
【分析】(1)原式先计算除法,再计算减法运算即可求出值;
(2)利用平方差公式和完全平方公式展开,再计算加减即可求出值.
【解答】解:(1)原式=3 ﹣
=2 ;
(2)原式=4﹣5﹣3+4 ﹣4
=﹣8+4 .
【点评】此题考查了二次根式的混合运算,熟练掌握运算法则是解本题的关键.
18.(10分)解方程组:
(1) ;
(2) .
【分析】(1)运用加减消元法解出 x的值,再运用代入消元法解出 y的值,即可作答;
(2)先去分母,再运用代入消元法解出 y的值,即可作答.
【解答】解:(1)因为 ,
所以②+①×2,得 11x=66,
解得 x=6,
把 x=6代入①,得 18+4y=16,
解得 ,
所以方程组的解为 ;
(2)因为 ,
所以整理①得 3x﹣3+2y+2=6,即 3x+2y=7,
所以整理②得 x=4﹣y,
把 x=4﹣y代入 3x+2y=7,
得 3×(4﹣y)+2y=7,
解得 y=5,
把 y=5代入 x=4﹣y,
解得 x=﹣1,
所以方程组的解为 .
【点评】本题考查了解二元一次方程组,能选择适当的方法解方程组是解此题的关键.
19.(8分)△ABC在平面直角坐标系中的位置如图所示,A、B、C三点在格点上.
(1)作出△ABC关于 x轴对称的△A1B1C1,并写出点 C1的坐标;
(2)在 y轴上求作点 D,使得 AD+BD最小,请你直接写出 D点坐标;
(3)若点 P为 x轴上一动点,且满足△BCP的面积为 1,请你直接写出 P点坐标.
【分析】(1)根据题意和图形,可以画出△ABC关于 x轴对称的△A1B1C1,并写出点 C1
的坐标;
(2)根据轴对称和两点之间线段,可以得到使得 AD+BD最小时点 D所在的位置,然后
写出 D点坐标即可;
(3)分 3种情况结合图形求解即可.
【解答】解:(1)如图所示,△A1B1C1即为所求,点 C1的坐标是(3,﹣2);
(2)作点 A 关于 y轴的对称点 A',连接 BA'与 y轴交于点 D,则此时 AD+BD最小,D
点坐标是(0,2).
(3)如图,当 P(1,0)时, .
如图,当 P点横坐标大于 1,时, ,不符
合题意;
当 P点横坐标小于 1时,同理可求 S△BCP<1,不符合题意;
综上可知,当△BCP的面积为 1时,P点坐标(1,0).
【点评】本题考查作图﹣轴对称图象、最短路径问题,坐标与图形的性质,解答本题的
关键是明确题意,利用数形结合的思想解答.
20.(8 分)某班级为表彰运动会表现优秀的同学,班主任老师安排小明和小红购买奖品,
图①,图 2是小明和小红购买奖品后的对话情境,根据信息解决问题,试计算两种笔记
本各买了多少本?
【分析】依题意,设 5元的笔记本买了 x本,8元的笔记本买了 y本,由图中信息列出二
元一次方程组,解方程组即可.
【解答】解:设 5元的笔记本买了 x本,8元的笔记本买了 y本,
由题意得:
,
整理得
解得:
所以 5元的笔记本买了 25本,8元的笔记本买了 15本.
【点评】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组
是解题的关键.
21.(8 分)为了积极响应国家新农村建设的号召,遂宁市某镇政府采用了移动宣讲的形式
进行广播宣传.如图,笔直的公路 MN的一侧点 A处有一村庄,村庄到公路 MN的距离
为 600m,假使宣讲车 P周围 1000m以内能听到广播宣传,宣讲车 P在公路 MN上沿 PN
方向行驶.
(1)村庄能否听到广播宣传?请说明理由.
(2)已知宣讲车的速度是 200m/min,如果村庄能听到广播宣传,那么总共能听多长时间?
【分析】(1)根据村庄 A到公路 MN的距离为 600米<1000米,即可得出村庄能听到广
播宣传.
(2)根据勾股定理得到 BP=BQ= =800(米),求得 PQ=1600米,即
可得出结果.
【解答】解:(1)村庄能听到广播宣传,理由如下:
∵村庄 A到公路 MN的距离为 600米<1000米,
∴村庄能听到广播宣传.
(2)如图:假设当宣传车行驶到 P点开始能听到广播,行驶到 Q点不能听到广播,
则 AP=AQ=1000米,AB=600米,
由勾股定理得:
BP=BQ= =800(米),
∴PQ=1600米,
∴能听到广播的时间为:1600÷200=8(分钟),
∴村庄总共能听到 8分钟的宣传.
【点评】本题考查了勾股定理的应用,结合生活实际,便于更好的理解题意是解题的关
键
22.(10分)张氏包装厂承接了一批纸盒加工任务,用如图①所示的长方形和正方形纸板
作侧面和底面,做成如图②所示的竖式与横式两种上面无盖的长方体纸盒(加工时接缝
材料不计).
(1)做 1个竖式纸盒和 2 个横式纸盒,需正方形纸板张 5 张(直接填空),需长方
形纸板 10 张(直接填空).
(2)若该厂购进正方形纸板 162张,长方形纸板 338张,问竖式纸盒、横式纸盒各加工
多少个,恰好能将购进的纸板全部用完?(要求列二元一次方程组解决此问题)
【分析】(1)利用需要正方形纸板张数=1×制作竖式纸盒个数+2×制作横式纸盒个数,
可求出所需正方形纸板张数,利用需要长方形纸板张数=4×制作竖式纸盒个数+3×制作
横式纸盒个数,即可求出所需长方形纸板张数;
(2)设加工竖式纸盒 x个,横式纸盒 y个,根据制作的两种纸盒正好使用正方形纸板 162
张、长方形纸板 338张,可得出关于 x,y的二元一次方程组,解之即可得出结论.
【解答】解:(1)∵1×1+2×2=5(张),4×1+3×2=10(张),
∴做 1个竖式纸盒和 2个横式纸盒,需正方形纸板张 5张,需长方形纸板 10张.
故答案为:5,10;
(2)设加工竖式纸盒 x个,横式纸盒 y个,
根据题意得: ,
解得: .
答:加工竖式纸盒 38个,横式纸盒 62个,恰好能将购进的纸板全部用完.
【点评】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组
是解题的关键.
23.(10分)小明在解决问题:已知 ,求 2a2﹣8a+1的值,他是这样分析与解答的:
∵ ,
∴ .
∴(a﹣2)2=3,即 a2﹣4a+4=3.
∴a2﹣4a=﹣1,
∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1.
请你根据小明的分析过程,解决如下问题:
(1)计算: = ﹣1 ;
(2)计算: + ;
(3)若 a= ,求 2a2﹣8a+1的值.
【分析】(1)直接分母有理化得出答案;
(2)直接分母有理化得出答案;
(3)根据题意得出 a的值,再得出 a2﹣4a=1,再把已知变形得出答案.
【解答】解:(1) = = ﹣1.
故答案为: ﹣1;
(2)原式=( ﹣1)+( ﹣ )+( ﹣ )+…+( ﹣ )
= ﹣1
=10﹣1
=9.
(3)因为 a= = +2,
所以 a﹣2= .所以(a﹣2)2=5,即 a2﹣4a+4=5.
所以 a2﹣4a=1.
所以 2a2﹣8a+1=2(a2﹣4a)+1=2×1+1=3.
【点评】此题主要考查了二次根式的混合运算以及二 3.次根式化简求值,正确化简二次
根式是解题关键.
24.(12分)在 A、B两地之间有服务区 C,甲车由 A地驶往服务区 C,乙车由 B地驶往 A
地,两车同时出发,匀速行驶.如图是甲、乙两车分别距离服务区 C的路程 y1、y2(单
位:千米)与乙车行驶时间 x(单位:小时)之间的函数图象,结合图象信息,解答下列
问题:
(1)甲车的速度是 70 千米/时;
(2)求图象中线段 DF的函数解析式;
(3)当两车距服务区 C的路程之和是 360千米时,直接写出此时乙车的行驶时间.
【分析】(1)根据函数图象,结合路程除以速度,即可求解;
(2)先求得乙车的速度,进而得出 F(9,420),待定系数求得解析式,即可求解;
(3)分别求得各段解析式,根据题意,列出一元一次方程,解方程,即可求解.
【解答】解:(1)由图象可知,甲车的平均速度为 =70(千米/小时),
故答案为:70;
(2)由图象可知,乙车的速度为 =60(千米/小时),
∴乙车到达 A地所用时间为 =7(小时),
∴乙车从 B地到 A地所用时间为 2+7=9(小时),
∴F(9,420),
设 DF所在直线的函数解析式为 y=kx+b(k≠0),
把 D(2,0)和 F(9,420)代入解析式得:
,
解得 ,
∴DF所在直线的函数解析式为 y2=60x﹣120;
(3)依题意得:y1=﹣70x+420(0≤x≤2),
y2= ,
设乙车的行驶 x小时后,两车距服务区 C的路程之和是 360千米,
①甲乙未相遇时,
则﹣70x+420﹣60x+120=360,
解得 x= ;
②当乙车经过服务区 C,
﹣70x+420+60x﹣120=360,
解得 x=﹣6(舍);
③当甲乙相遇后,
60x﹣120=360,
解得 x=8.
综上所述,当乙车 小时或 8小时时两车距服务区 C的路程之和是 360千米.
【点评】本题考查了一次函数的应用及一元一次方程的应用,解题的关键是根据题意结
合图象说出其图象表示的实际意义,这样便于理解题意及正确的解题.
25.(12分)如图 1,已知直线 l1:y=﹣x+5与 x轴交于点 A,与 y轴交于点 B,直线 l2与 y
轴交于点 C(0,﹣1),与直线 l1交于点 D(2,t).
(1)求直线 l2的解析式;
(2)如图 2,若点 P在直线 l1上,过点 P作 PQ∥y轴交 l2于点 Q,交 x轴于点 G,使 S
△PCG=2S△QCG,求此时 P点的坐标;
(3)将直线 l1:y=﹣x+5向左平移 10个单位得直线 l3交 x轴于点 E,点 F是点 C关于
原点的对称点.过点 F作直线 l4∥x轴.在直线 l4上是否存在动点 M,使得△MCE为等
腰三角形?若存在,请直接写出点 M的坐标;若不存在,请说明理由.
【分析】(1 )把点 D坐标代入直线 l1:y=﹣x+5求出 t的值,利用待定系数法即可求解;
(2 )根据三角形面积公式可得 PG=2QG,即可求解;
(3)设 M(a,1),则 MC= = ,ME= ,CE=
,分 ME=MC,CE=MC,ME=CE三种情况列式求解即可.
【解答】解:(1)∵D(2,t)在直线 l1:y=﹣x+5上,
∴t=﹣2+5=3,
∴D(2,3),
设直线 l2的解析式为 y=kx+b,
将点 C,D代入得, ,
解得, ,
所以,直线 l2的解析式为 y=2x﹣1;
(2)设 P(a,5﹣a),
∵PQ∥y轴,
G(a,0),Q(a,2a﹣1),
分两种情况:
①如图,点 P、Q在 x轴两侧,
∵S△PCG= PG |a|,S△QCG= GQ |a|且 S△PCG=2S△QCG,
∴PG=2QG,
∴5﹣a=2(1﹣2a),
解得:a=﹣1,
∴P点的坐标为(﹣1,6);
②如图,点 P、Q都在 x轴上方,
∵S△PCG= PG |a|,S△QCG= GQ |a|且 S△PCG=2S△QCG,
∴PG=2QG,
∴5﹣a=2(2a﹣1),
解得:a= ,
∴P点的坐标为( , );
综上,P点的坐标为(﹣1,6)或( , );
(3)存在,理由如下:
对于直线 l1:y=﹣x+5,
当 x=0时,y=5;当 y=0时,x=5.
∴A(5.0),B(0.5),
∵将直线 l1:y=﹣x+5 向左平移 10个单位得直线 l3交 x轴于点 E,点 F是点 C关于原
点的对称点.点 C(0,﹣1),
∴E﹣5.0),N(0.﹣5),F(0,1),
如图,
∵将直线 l1:y=﹣x+5向左平移 10个单位得直线 l3,
∴直线 l3:y=﹣x﹣5,
又∵F(0.1)
∴l4的解析式为:y=1,
设 M(a,1),则 MC= = ,ME= ,CE= ,
当△MCE为等腰三角形,有:
①ME=MC时, = ,
解得,a=﹣ ,即 M(﹣ ,1),
②CE=MC时, = ,
解得:a= 或 a=﹣ ,
即 M( ,1).M(﹣ ,1),
③ME=CE时, = ,
解得,a=0或 a=﹣10(此时三点共线,不构成三角形,舍去),
即 M(0,1),
综上,点 M的坐标为:M(﹣ ,1)或 M( ,1)或 M(﹣ ,1)或 M(0,1).
【点评】本题为一次函数综合题,解题的关键是熟练掌握待定系数法求函数解析式、三角形
的面积公式,等腰三角形的性质等知识,其中(3)要注意分类求解,避免遗漏.
数学试卷
一.选择题(每小题 4 分,共 40 分)
1.(4分)以下各数﹣3, , ,π,1.9191191119…(每两个 9之间依次多一个 1),其
中无理数的个数是( )
A.1个 B.2个 C.3个 D.4个
2.(4分)平面直角坐标系中,与点 A(﹣2,3)关于 x轴对称的点的坐标为( )
A.(2,3) B.(﹣2,3) C.(﹣3,2) D.(﹣2,﹣3)
3.(4分)如图所示的数轴被墨迹污染了,则下列选项中可能被覆盖住的数是( )
A. B.﹣ C.﹣ D.﹣
4.(4分)已知 A(﹣ ,y1)、B(﹣ ,y2)、C(1,y3)是一次函数 y=﹣3x+b的图象上
三点,则 y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y1<y3 C.y3<y1<y2 D.y3<y2<y1
5.(4分)一次函数 y=kx和 y=﹣x+3的图象如图所示,则二元一次方程组 的解
是( )
A. B. C. D.
6.(4分)已知 是二元一次方程组 的解,则 a﹣b的值为( )
A.3 B.2 C.1 D.﹣1
7.(4分)一次函数 y1=mx+n与 y2=mnx(m、n为常数,且 mn≠0)在同一平面直角坐标
内的图象可能是( )
A. B.
C. D.
8.(4分)母亲节来临,小明去花店为妈妈准备节日礼物.已知康乃馨每支 2元,百合每支
3元.小明将 20元钱全部用于购买这两种花(两种花都买),小明的购买方案共有( )
A.2种 B.3种 C.4种 D.5种
9.(4分)“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如
图所示的“赵爽弦图”是由四个全等的直角三角形(如图 1)拼成的一个大正方形(如图
2).设直角三角形较长
直角边长为 a,较短直角边长为 b.若 ab=8,大正方形的面积为 25,则图 2中 EF的长
为( )
A.3 B.4 C. D.
10.(4分)如图,直线 y=2x﹣6与 x轴、y轴分别交于 A,B两点,C在 y轴的正半轴上,
D在直线 AB上,且 CB=10,CD=OD.若点 P为线段 AB上的一个动点,且 P关于 x
轴的对称点 Q总在△OCD内(不包括边界),则点 P的横坐标 m的取值范围为( )
A. B. C. D.
二.填空题(每小题 4 分,共 24 分)
11.(4分)10的算术平方根是 .
12.(4分)如图,在数轴上点 D表示的实数为 .
13.(4分)在平面直角坐标系中,点 P(m,3),点 Q(2﹣2m,m﹣3),且 PQ∥y轴,则
m= .
14.(4分)一支原长为 12cm的蜡烛,点燃后其剩余长度与燃烧时间之间的关系如下表:
燃烧时间/分 10 20 30 40 50 …
剩余长度/cm 11.2 10.4 9.6 8.8 8 …
则这支蜡烛最多可燃烧 分钟.
15.(4分)利用两块完全一样的长方体木块测量一张桌子的高度,首先按图①所示的方式
放置,图示距离为 110cm;再交换两木块的位置,按图②所示的方式放置,图示距离为
60cm,则桌子的高度等于 cm.
16.(4分)已知一次函数 y=ax﹣a+2(a为常数,且 a≠0).若当﹣1≤x≤4时,函数有最
大值 7,则 a的值为 .
三、解答题(共 9 个小题,共 86 分)
17.(8分)化简与求值:
(1) ;
(2) .
18.(10分)解方程组:
(1) ;
(2) .
19.(8分)△ABC在平面直角坐标系中的位置如图所示,A、B、C三点在格点上.
(1)作出△ABC关于 x轴对称的△A1B1C1,并写出点 C1的坐标;
(2)在 y轴上求作点 D,使得 AD+BD最小,请你直接写出 D点坐标;
(3)若点 P为 x轴上一动点,且满足△BCP的面积为 1,请你直接写出 P点坐标.
20.(8 分)某班级为表彰运动会表现优秀的同学,班主任老师安排小明和小红购买奖品,
图①,图 2是小明和小红购买奖品后的对话情境,根据信息解决问题,试计算两种笔记
本各买了多少本?
21.(8 分)为了积极响应国家新农村建设的号召,遂宁市某镇政府采用了移动宣讲的形式
进行广播宣传.如图,笔直的公路 MN的一侧点 A处有一村庄,村庄到公路 MN的距离
为 600m,假使宣讲车 P周围 1000m以内能听到广播宣传,宣讲车 P在公路 MN上沿 PN
方向行驶.
(1)村庄能否听到广播宣传?请说明理由.
(2)已知宣讲车的速度是 200m/min,如果村庄能听到广播宣传,那么总共能听多长时间?
22.(10分)张氏包装厂承接了一批纸盒加工任务,用如图①所示的长方形和正方形纸板
作侧面和底面,做成如图②所示的竖式与横式两种上面无盖的长方体纸盒(加工时接缝
材料不计).
(1)做 1个竖式纸盒和 2个横式纸盒,需正方形纸板张 张(直接填空),需长
方形纸板 张(直接填空).
(2)若该厂购进正方形纸板 162张,长方形纸板 338张,问竖式纸盒、横式纸盒各加工
多少个,恰好能将购进的纸板全部用完?(要求列二元一次方程组解决此问题)
23.(10分)小明在解决问题:已知 ,求 2a2﹣8a+1的值,他是这样分析与解答的:
∵ ,
∴ .
∴(a﹣2)2=3,即 a2﹣4a+4=3.
∴a2﹣4a=﹣1,
∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1.
请你根据小明的分析过程,解决如下问题:
(1)计算: = ;
(2)计算: + ;
(3)若 a= ,求 2a2﹣8a+1的值.
24.(12分)在 A、B两地之间有服务区 C,甲车由 A地驶往服务区 C,乙车由 B地驶往 A
地,两车同时出发,匀速行驶.如图是甲、乙两车分别距离服务区 C的路程 y1、y2(单
位:千米)与乙车行驶时间 x(单位:小时)之间的函数图象,结合图象信息,解答下列
问题:
(1)甲车的速度是 千米/时;
(2)求图象中线段 DF的函数解析式;
(3)当两车距服务区 C的路程之和是 360千米时,直接写出此时乙车的行驶时间.
25.(12分)如图 1,已知直线 l1:y=﹣x+5与 x轴交于点 A,与 y轴交于点 B,直线 l2与 y
轴交于点 C(0,﹣1),与直线 l1交于点 D(2,t).
(1)求直线 l2的解析式;
(2)如图 2,若点 P在直线 l1上,过点 P作 PQ∥y轴交 l2于点 Q,交 x轴于点 G,使 S
△PCG=2S△QCG,求此时 P点的坐标;
(3)将直线 l1:y=﹣x+5向左平移 10个单位得直线 l3交 x轴于点 E,点 F是点 C关于
原点的对称点.过点 F作直线 l4∥x轴.在直线 l4上是否存在动点 M,使得△MCE为等
腰三角形?若存在,请直接写出点 M的坐标;若不存在,请说明理由.
2023-2024 学年山东省济南市历城区稼轩学校八年级(上)期中
数学试卷
参考答案与试题解析
一.选择题(每小题 4 分,共 40 分)
1.(4分)以下各数﹣3, , ,π,1.9191191119…(每两个 9之间依次多一个 1),其
中无理数的个数是( )
A.1个 B.2个 C.3个 D.4个
【分析】根据无理数的定义:不能表示成两个整数之商的数即不循环的无限小数即可求
解.
【解答】解:﹣3是整数,不是无理数,
是无限不循环小数,是无理数,
是分数,不是无理数,
π是无限不循环小数,是无理数,
1.9191191119…(每两个 9之间依次多一个 1)是无限不循环小数,是无理数,
符合题意的有 3个,
故选:C.
【点评】本题主要考查了无理数,掌握无理数的定义是解题的关键.
2.(4分)平面直角坐标系中,与点 A(﹣2,3)关于 x轴对称的点的坐标为( )
A.(2,3) B.(﹣2,3) C.(﹣3,2) D.(﹣2,﹣3)
【分析】根据“关于 x轴对称的点,横坐标相同,纵坐标互为相反数”解答即可.
【解答】解:点 A(﹣2,3)关于 x轴对称的点的坐标为(﹣2,﹣3).
故选:D.
【点评】本题考查了关于 x轴、y轴对称的点的坐标,解决本题的关键是掌握好对称点的
坐标规律:(1)关于 x轴对称的点,横坐标相同,纵坐标互为相反数;(2)关于 y轴对
称的点,纵坐标相同,横坐标互为相反数.
3.(4分)如图所示的数轴被墨迹污染了,则下列选项中可能被覆盖住的数是( )
A. B.﹣ C.﹣ D.﹣
【分析】根据题意可知在﹣3与﹣2之间,据此判断,观察选项中的四个数哪一个在这个
范围内即可.
【解答】解:设被覆盖住的数是 x,
由图可知:﹣3<x<﹣2,
∵﹣ <﹣ ,即 <﹣3,不在此范围内,故 A错;
∵﹣ ≈﹣1.732>﹣2,不在此范围内,故 C错;
∵﹣ ≈﹣1.414>﹣2,不在此范围内,故 D错;
所以 B正确,
故选:B.
【点评】本题考查有理数的大小比较,是基础题.
4.(4分)已知 A(﹣ ,y1)、B(﹣ ,y2)、C(1,y3)是一次函数 y=﹣3x+b的图象上
三点,则 y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y1<y3 C.y3<y1<y2 D.y3<y2<y1
【分析】利用一次函数图象上点的坐标特征可求出 y1,y2,y3的值,比较后可得出结论.
【解答】解:∵A(﹣ ,y1)、B(﹣ ,y2)、C(1,y3)是一次函数 y=﹣3x+b的图象
上三点,
∴y1=1+b,y2= +b,y3=﹣3+b.
∵﹣3+b<1+b< +b,
∴y3<y1<y2.
故选:C.
【点评】本题考查了一次函数图象上点的坐标特征,利用一次函数图象上点的坐标特征,
求出 y1,y2,y3的值是解题的关键.
5.(4分)一次函数 y=kx和 y=﹣x+3的图象如图所示,则二元一次方程组 的解
是( )
A. B. C. D.
【分析】两个一次函数图象的交点坐标就是两函数组成的方程组的解.
【解答】解:∵一次函数 y=kx和 y=﹣x+3的图象交于点(1,2),
∴二元一次方程组 的解是 ,
故选:A.
【点评】此题主要考查了一次函数与二元一次方程组,掌握二元一次方程(组)与一次
函数的关系是解题的关键.
6.(4分)已知 是二元一次方程组 的解,则 a﹣b的值为( )
A.3 B.2 C.1 D.﹣1
【分析】把 x=2.y=1代入方程组 得出方程组 求出方程组的解即
可.
【解答】解:把 x=2.y=1代入方程组 得:
①+②得:4a=8,
解得:a=2,
把 a=2代入①得:4+b=7,
解得:b=3,
a﹣b=2﹣3=﹣1,
故选:D.
【点评】本题考查了二元一次方程组的解,解二元一次方程组的应用,解此题的关键是
能得出关于 a、b的方程组,难度适中.
7.(4分)一次函数 y1=mx+n与 y2=mnx(m、n为常数,且 mn≠0)在同一平面直角坐标
内的图象可能是( )
A. B.
C. D.
【分析】根据一次函数与正比例函数的性质对四个选项进行逐一分析即可.
【解答】解:A、由一次函数的图象可知,m<0,n>0,故 mn<0;由正比例函数的图
象可知 mn<0,两结论一致,故本选项符合题意;
B、由一次函数的图象可知,m<0,n>0,故 mn<0;由正比例函数的图象可知 mn>0,
两结论不一致,故本选项不符合题意;
C、由一次函数的图象可知,m>0,n>0,故 mn>0;由正比例函数的图象可知 mn<0,
两结论不一致,故本选项不符合题意;
D、由一次函数的图象可知,m>0,n<0,故 mn<0;由正比例函数的图象可知 mn>0,
两结论不一致,故本选项不符合题意.
故选:A.
【点评】此题主要考查了一次函数的图象性质,要掌握它的性质才能灵活解题.
一次函数 y=kx+b的图象有四种情况:
①当 k>0,b>0时,函数 y=kx+b的图象经过第一、二、三象限;
②当 k>0,b<0时,函数 y=kx+b的图象经过第一、三、四象限;
③当 k<0,b>0时,函数 y=kx+b的图象经过第一、二、四象限;
④当 k<0,b<0时,函数 y=kx+b的图象经过第二、三、四象限.
8.(4分)母亲节来临,小明去花店为妈妈准备节日礼物.已知康乃馨每支 2元,百合每支
3元.小明将 20元钱全部用于购买这两种花(两种花都买),小明的购买方案共有( )
A.2种 B.3种 C.4种 D.5种
【分析】设可以购买 x支康乃馨,y支百合,根据总价=单价×数量,即可得出关于 x,
y的二元一次方程,结合 x,y均为正整数即可得出小明有 3种购买方案.
【解答】解:设可以购买 x支康乃馨,y支百合,
依题意,得:2x+3y=20,
∴x=10﹣ y.
∵x,y均为正整数,
∴ 或 或 ,
∴小明有 3种购买方案.
故选:B.
【点评】本题考查了二元一次方程的应用,找准等量关系,正确列出二元一次方程是解
题的关键.
9.(4分)“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如
图所示的“赵爽弦图”是由四个全等的直角三角形(如图 1)拼成的一个大正方形(如图
2).设直角三角形较长
直角边长为 a,较短直角边长为 b.若 ab=8,大正方形的面积为 25,则图 2中 EF的长
为( )
A.3 B.4 C. D.
【分析】由图形 2可知,中间四边形的边长为(a﹣b)的小正方形,由大正方形的面积
由四个全等的直角三角形加中间小正方形的面积得出 =25,再结合 ab
=8即可得出(a﹣b)的值,再根据勾股定理即可求出 EF的长.
【解答】解:由图形 2可知,中间四边形的边长为(a﹣b)的小正方形,
∵大正方形的面积为 25,
∴AB2=25,
又∵大正方形的面积由四个全等的直角三角形加中间小正方形的面积,
∴ =25,
∴(a﹣b)2+2ab=25,
∴(a﹣b)2+2×8=25,
∴(a﹣b)=3(负值已舍),
即图 2中小正方形的边长为 3,
∴EF= =3 ,
故选:D.
【点评】本题考查了勾股定理的证明,勾股定理,正确得出大正方形的面积表示方法是
解题的关键.
10.(4分)如图,直线 y=2x﹣6与 x轴、y轴分别交于 A,B两点,C在 y轴的正半轴上,
D在直线 AB上,且 CB=10,CD=OD.若点 P为线段 AB上的一个动点,且 P关于 x
轴的对称点 Q总在△OCD内(不包括边界),则点 P的横坐标 m的取值范围为( )
A. B. C. D.
【分析】先求出 A(3,0)、B(0,﹣6),进而求出 C(0,4),再由 CD=OD可知点 D
在线段 OC的垂直平分线上,即在直线 y=2 上,则 D(4,2),利用待定系数法求出直
线 CD和直线 OD的解析式,根据关于 x轴对称的点横坐标相同及坐标互为相反数求出
点 Q的坐标,再根据点 Q在△OCD内,则当 x=m时,点 Q的纵坐标在直线 CD和直线
OD二者的函数值之间,由此建立不等式求解即可.
【解答】解:在 y=2x﹣6中,当 x=0时,y=2x﹣6=﹣6,当 y=2x﹣6=0时,x=3,
∴A(3,0),B(0,﹣6),
∵C在 y轴的正半轴上,CB=10,
∴C(0,4),
∵CD=OD.
∴点 D在线段 OC的垂直平分线上,即在直线 y=2上,
在 y=2x﹣6中,当 y=2x﹣6=2时,x=4,
∴D(4,2);
设直线 CD解析式为 y=kx+b,
,
∴
∴直线 CD解析式为 y=﹣ x+4.
同理可得直线 OD的解析式为 y= x,
∵点 P为线段 AB上的一个动点,且其横坐标为 m,
∴P(m,2m﹣6),
∵P、Q关于 x轴对称,
∴Q(m,6﹣2m),
∵点 Q总在△OCD内(不包括边界),
∴ m<6﹣2m<﹣ m+4.
解得 <m< .
故选:D.
【点评】本题主要考查了一次函数与几何综合,坐标与图形变化一轴对称,正确理解题
意得到点 Q在△OCD内,则当 x=m时,点 Q的纵坐标在直线 CD和直线 OD二者的函
数值之间是解题的关键.
二.填空题(每小题 4 分,共 24 分)
11.(4分)10的算术平方根是 .
【分析】根据算术平方根的定义进行解答即可.
【解答】解:10的算术平方根是 .
故答案为: .
【点评】本题主要考查了求一个数的算术平方根,解题的关键是熟练掌握算术平方根的
定义.
12.(4分)如图,在数轴上点 D表示的实数为 1﹣ .
【分析】根据勾股定理求出圆弧的半径,再根据点 D的位置可得答案.
【解答】解:∵AB=2﹣1=1,AC=2,
∴BC= = ,
∴点 D表示的数为 1﹣ ,
故答案为:1﹣ .
【点评】本题考查了实数与数轴,勾股定理的应用,体现了数形结合的数学思想,解题
时注意点 D在数轴的负半轴上.
13.(4分)在平面直角坐标系中,点 P(m,3),点 Q(2﹣2m,m﹣3),且 PQ∥y轴,则
m= .
【分析】根据平行于 y轴的直线上的点横坐标相同求出 m的值即可
【解答】解:∵P(m,3),点 Q(2﹣2m,m﹣3),且 PQ∥y轴,
∴m=2﹣2m,
解得: ,
故答案为: .
【点评】本题主要考查了坐标与图形,熟知平行于 y轴的直线上的点横坐标相同是解题
的关键.
14.(4分)一支原长为 12cm的蜡烛,点燃后其剩余长度与燃烧时间之间的关系如下表:
燃烧时间/分 10 20 30 40 50 …
剩余长度/cm 11.2 10.4 9.6 8.8 8 …
则这支蜡烛最多可燃烧 150 分钟.
【分析】设这支蜡烛剩余长度为 ycm,燃烧时间为 x分钟,根据蜡烛剩余长度与燃烧时
间的关系可知每燃烧 10分钟,蜡烛剩余长度减少 0.8cm,由此建立 y与 x之间的函数关
系式,再求出 y=0时的 x值即可.
【解答】解:设这支蜡烛剩余长度为 ycm,燃烧时间为 x分钟,由表可知,每燃烧 10分
钟,蜡烛剩余长度减少 0.8cm,
则 y=12﹣0.08x,
当 y=0时,12﹣0.08x=0,
解得 x=150,
所以这支蜡烛最多可燃烧 150分钟,
故答案为:150.
【点评】本题考查了一次函数的实际应用,正确求出函数关系式是解题关键.
15.(4分)利用两块完全一样的长方体木块测量一张桌子的高度,首先按图①所示的方式
放置,图示距离为 110cm;再交换两木块的位置,按图②所示的方式放置,图示距离为
60cm,则桌子的高度等于 85 cm.
【分析】根据“按图①所示的方式放置,图示距离为 110cm”和“图②所示的方式放置,
图示距离为 60cm”列方程组求解.
【解答】解:设桌子的高度为 xcm,长方体木块的长为 acm,宽为 bcm,
则: ,
①+②得:2x=170,
解得:x=85,
故答案为:85.
【点评】本题考查了三元一次方程组的应用,找到相等关系是解题的关键.
16.(4分)已知一次函数 y=ax﹣a+2(a为常数,且 a≠0).若当﹣1≤x≤4时,函数有最
大值 7,则 a的值为 或﹣ .
【分析】分类讨论:a>0 时,y随 x的增大而增大,所以当 x=2 时,y有最大值 2,然
后把 y=2代入函数关系式可计算出对应 a的值;a<0时,y随 x的增大而减小,所以当
x=﹣1时,y有最大值 2,然后把 x=﹣1代入函数关系式可计算对应 a的值.
【解答】解:①a>0时,y随 x的增大而增大,
则当 x=4时,y有最大值 7,把 x=4,y=7代入函数关系式得 7=4a﹣a+2,解得 a= ;
②a<0时,y随 x的增大而减小,
则当 x=﹣1时,y有最大值 7,把 x=﹣1代入函数关系式得 7=﹣a﹣a+2,解得 a=﹣ ,
所以 a= 或 a=﹣ ,
故答案为 或﹣ .
【点评】本题考查了一次函数的性质:k>0,y随 x的增大而增大,函数从左到右上升;
k<0,y随 x的增大而减小,函数从左到右下降.由于 y=kx+b与 y轴交于(0,b),当 b
>0时,(0,b)在 y轴的正半轴上,直线与 y轴交于正半轴;当 b<0 时,(0,b)在 y
轴的负半轴,直线与 y轴交于负半轴.
三、解答题(共 9 个小题,共 86 分)
17.(8分)化简与求值:
(1) ;
(2) .
【分析】(1)原式先计算除法,再计算减法运算即可求出值;
(2)利用平方差公式和完全平方公式展开,再计算加减即可求出值.
【解答】解:(1)原式=3 ﹣
=2 ;
(2)原式=4﹣5﹣3+4 ﹣4
=﹣8+4 .
【点评】此题考查了二次根式的混合运算,熟练掌握运算法则是解本题的关键.
18.(10分)解方程组:
(1) ;
(2) .
【分析】(1)运用加减消元法解出 x的值,再运用代入消元法解出 y的值,即可作答;
(2)先去分母,再运用代入消元法解出 y的值,即可作答.
【解答】解:(1)因为 ,
所以②+①×2,得 11x=66,
解得 x=6,
把 x=6代入①,得 18+4y=16,
解得 ,
所以方程组的解为 ;
(2)因为 ,
所以整理①得 3x﹣3+2y+2=6,即 3x+2y=7,
所以整理②得 x=4﹣y,
把 x=4﹣y代入 3x+2y=7,
得 3×(4﹣y)+2y=7,
解得 y=5,
把 y=5代入 x=4﹣y,
解得 x=﹣1,
所以方程组的解为 .
【点评】本题考查了解二元一次方程组,能选择适当的方法解方程组是解此题的关键.
19.(8分)△ABC在平面直角坐标系中的位置如图所示,A、B、C三点在格点上.
(1)作出△ABC关于 x轴对称的△A1B1C1,并写出点 C1的坐标;
(2)在 y轴上求作点 D,使得 AD+BD最小,请你直接写出 D点坐标;
(3)若点 P为 x轴上一动点,且满足△BCP的面积为 1,请你直接写出 P点坐标.
【分析】(1)根据题意和图形,可以画出△ABC关于 x轴对称的△A1B1C1,并写出点 C1
的坐标;
(2)根据轴对称和两点之间线段,可以得到使得 AD+BD最小时点 D所在的位置,然后
写出 D点坐标即可;
(3)分 3种情况结合图形求解即可.
【解答】解:(1)如图所示,△A1B1C1即为所求,点 C1的坐标是(3,﹣2);
(2)作点 A 关于 y轴的对称点 A',连接 BA'与 y轴交于点 D,则此时 AD+BD最小,D
点坐标是(0,2).
(3)如图,当 P(1,0)时, .
如图,当 P点横坐标大于 1,时, ,不符
合题意;
当 P点横坐标小于 1时,同理可求 S△BCP<1,不符合题意;
综上可知,当△BCP的面积为 1时,P点坐标(1,0).
【点评】本题考查作图﹣轴对称图象、最短路径问题,坐标与图形的性质,解答本题的
关键是明确题意,利用数形结合的思想解答.
20.(8 分)某班级为表彰运动会表现优秀的同学,班主任老师安排小明和小红购买奖品,
图①,图 2是小明和小红购买奖品后的对话情境,根据信息解决问题,试计算两种笔记
本各买了多少本?
【分析】依题意,设 5元的笔记本买了 x本,8元的笔记本买了 y本,由图中信息列出二
元一次方程组,解方程组即可.
【解答】解:设 5元的笔记本买了 x本,8元的笔记本买了 y本,
由题意得:
,
整理得
解得:
所以 5元的笔记本买了 25本,8元的笔记本买了 15本.
【点评】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组
是解题的关键.
21.(8 分)为了积极响应国家新农村建设的号召,遂宁市某镇政府采用了移动宣讲的形式
进行广播宣传.如图,笔直的公路 MN的一侧点 A处有一村庄,村庄到公路 MN的距离
为 600m,假使宣讲车 P周围 1000m以内能听到广播宣传,宣讲车 P在公路 MN上沿 PN
方向行驶.
(1)村庄能否听到广播宣传?请说明理由.
(2)已知宣讲车的速度是 200m/min,如果村庄能听到广播宣传,那么总共能听多长时间?
【分析】(1)根据村庄 A到公路 MN的距离为 600米<1000米,即可得出村庄能听到广
播宣传.
(2)根据勾股定理得到 BP=BQ= =800(米),求得 PQ=1600米,即
可得出结果.
【解答】解:(1)村庄能听到广播宣传,理由如下:
∵村庄 A到公路 MN的距离为 600米<1000米,
∴村庄能听到广播宣传.
(2)如图:假设当宣传车行驶到 P点开始能听到广播,行驶到 Q点不能听到广播,
则 AP=AQ=1000米,AB=600米,
由勾股定理得:
BP=BQ= =800(米),
∴PQ=1600米,
∴能听到广播的时间为:1600÷200=8(分钟),
∴村庄总共能听到 8分钟的宣传.
【点评】本题考查了勾股定理的应用,结合生活实际,便于更好的理解题意是解题的关
键
22.(10分)张氏包装厂承接了一批纸盒加工任务,用如图①所示的长方形和正方形纸板
作侧面和底面,做成如图②所示的竖式与横式两种上面无盖的长方体纸盒(加工时接缝
材料不计).
(1)做 1个竖式纸盒和 2 个横式纸盒,需正方形纸板张 5 张(直接填空),需长方
形纸板 10 张(直接填空).
(2)若该厂购进正方形纸板 162张,长方形纸板 338张,问竖式纸盒、横式纸盒各加工
多少个,恰好能将购进的纸板全部用完?(要求列二元一次方程组解决此问题)
【分析】(1)利用需要正方形纸板张数=1×制作竖式纸盒个数+2×制作横式纸盒个数,
可求出所需正方形纸板张数,利用需要长方形纸板张数=4×制作竖式纸盒个数+3×制作
横式纸盒个数,即可求出所需长方形纸板张数;
(2)设加工竖式纸盒 x个,横式纸盒 y个,根据制作的两种纸盒正好使用正方形纸板 162
张、长方形纸板 338张,可得出关于 x,y的二元一次方程组,解之即可得出结论.
【解答】解:(1)∵1×1+2×2=5(张),4×1+3×2=10(张),
∴做 1个竖式纸盒和 2个横式纸盒,需正方形纸板张 5张,需长方形纸板 10张.
故答案为:5,10;
(2)设加工竖式纸盒 x个,横式纸盒 y个,
根据题意得: ,
解得: .
答:加工竖式纸盒 38个,横式纸盒 62个,恰好能将购进的纸板全部用完.
【点评】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组
是解题的关键.
23.(10分)小明在解决问题:已知 ,求 2a2﹣8a+1的值,他是这样分析与解答的:
∵ ,
∴ .
∴(a﹣2)2=3,即 a2﹣4a+4=3.
∴a2﹣4a=﹣1,
∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1.
请你根据小明的分析过程,解决如下问题:
(1)计算: = ﹣1 ;
(2)计算: + ;
(3)若 a= ,求 2a2﹣8a+1的值.
【分析】(1)直接分母有理化得出答案;
(2)直接分母有理化得出答案;
(3)根据题意得出 a的值,再得出 a2﹣4a=1,再把已知变形得出答案.
【解答】解:(1) = = ﹣1.
故答案为: ﹣1;
(2)原式=( ﹣1)+( ﹣ )+( ﹣ )+…+( ﹣ )
= ﹣1
=10﹣1
=9.
(3)因为 a= = +2,
所以 a﹣2= .所以(a﹣2)2=5,即 a2﹣4a+4=5.
所以 a2﹣4a=1.
所以 2a2﹣8a+1=2(a2﹣4a)+1=2×1+1=3.
【点评】此题主要考查了二次根式的混合运算以及二 3.次根式化简求值,正确化简二次
根式是解题关键.
24.(12分)在 A、B两地之间有服务区 C,甲车由 A地驶往服务区 C,乙车由 B地驶往 A
地,两车同时出发,匀速行驶.如图是甲、乙两车分别距离服务区 C的路程 y1、y2(单
位:千米)与乙车行驶时间 x(单位:小时)之间的函数图象,结合图象信息,解答下列
问题:
(1)甲车的速度是 70 千米/时;
(2)求图象中线段 DF的函数解析式;
(3)当两车距服务区 C的路程之和是 360千米时,直接写出此时乙车的行驶时间.
【分析】(1)根据函数图象,结合路程除以速度,即可求解;
(2)先求得乙车的速度,进而得出 F(9,420),待定系数求得解析式,即可求解;
(3)分别求得各段解析式,根据题意,列出一元一次方程,解方程,即可求解.
【解答】解:(1)由图象可知,甲车的平均速度为 =70(千米/小时),
故答案为:70;
(2)由图象可知,乙车的速度为 =60(千米/小时),
∴乙车到达 A地所用时间为 =7(小时),
∴乙车从 B地到 A地所用时间为 2+7=9(小时),
∴F(9,420),
设 DF所在直线的函数解析式为 y=kx+b(k≠0),
把 D(2,0)和 F(9,420)代入解析式得:
,
解得 ,
∴DF所在直线的函数解析式为 y2=60x﹣120;
(3)依题意得:y1=﹣70x+420(0≤x≤2),
y2= ,
设乙车的行驶 x小时后,两车距服务区 C的路程之和是 360千米,
①甲乙未相遇时,
则﹣70x+420﹣60x+120=360,
解得 x= ;
②当乙车经过服务区 C,
﹣70x+420+60x﹣120=360,
解得 x=﹣6(舍);
③当甲乙相遇后,
60x﹣120=360,
解得 x=8.
综上所述,当乙车 小时或 8小时时两车距服务区 C的路程之和是 360千米.
【点评】本题考查了一次函数的应用及一元一次方程的应用,解题的关键是根据题意结
合图象说出其图象表示的实际意义,这样便于理解题意及正确的解题.
25.(12分)如图 1,已知直线 l1:y=﹣x+5与 x轴交于点 A,与 y轴交于点 B,直线 l2与 y
轴交于点 C(0,﹣1),与直线 l1交于点 D(2,t).
(1)求直线 l2的解析式;
(2)如图 2,若点 P在直线 l1上,过点 P作 PQ∥y轴交 l2于点 Q,交 x轴于点 G,使 S
△PCG=2S△QCG,求此时 P点的坐标;
(3)将直线 l1:y=﹣x+5向左平移 10个单位得直线 l3交 x轴于点 E,点 F是点 C关于
原点的对称点.过点 F作直线 l4∥x轴.在直线 l4上是否存在动点 M,使得△MCE为等
腰三角形?若存在,请直接写出点 M的坐标;若不存在,请说明理由.
【分析】(1 )把点 D坐标代入直线 l1:y=﹣x+5求出 t的值,利用待定系数法即可求解;
(2 )根据三角形面积公式可得 PG=2QG,即可求解;
(3)设 M(a,1),则 MC= = ,ME= ,CE=
,分 ME=MC,CE=MC,ME=CE三种情况列式求解即可.
【解答】解:(1)∵D(2,t)在直线 l1:y=﹣x+5上,
∴t=﹣2+5=3,
∴D(2,3),
设直线 l2的解析式为 y=kx+b,
将点 C,D代入得, ,
解得, ,
所以,直线 l2的解析式为 y=2x﹣1;
(2)设 P(a,5﹣a),
∵PQ∥y轴,
G(a,0),Q(a,2a﹣1),
分两种情况:
①如图,点 P、Q在 x轴两侧,
∵S△PCG= PG |a|,S△QCG= GQ |a|且 S△PCG=2S△QCG,
∴PG=2QG,
∴5﹣a=2(1﹣2a),
解得:a=﹣1,
∴P点的坐标为(﹣1,6);
②如图,点 P、Q都在 x轴上方,
∵S△PCG= PG |a|,S△QCG= GQ |a|且 S△PCG=2S△QCG,
∴PG=2QG,
∴5﹣a=2(2a﹣1),
解得:a= ,
∴P点的坐标为( , );
综上,P点的坐标为(﹣1,6)或( , );
(3)存在,理由如下:
对于直线 l1:y=﹣x+5,
当 x=0时,y=5;当 y=0时,x=5.
∴A(5.0),B(0.5),
∵将直线 l1:y=﹣x+5 向左平移 10个单位得直线 l3交 x轴于点 E,点 F是点 C关于原
点的对称点.点 C(0,﹣1),
∴E﹣5.0),N(0.﹣5),F(0,1),
如图,
∵将直线 l1:y=﹣x+5向左平移 10个单位得直线 l3,
∴直线 l3:y=﹣x﹣5,
又∵F(0.1)
∴l4的解析式为:y=1,
设 M(a,1),则 MC= = ,ME= ,CE= ,
当△MCE为等腰三角形,有:
①ME=MC时, = ,
解得,a=﹣ ,即 M(﹣ ,1),
②CE=MC时, = ,
解得:a= 或 a=﹣ ,
即 M( ,1).M(﹣ ,1),
③ME=CE时, = ,
解得,a=0或 a=﹣10(此时三点共线,不构成三角形,舍去),
即 M(0,1),
综上,点 M的坐标为:M(﹣ ,1)或 M( ,1)或 M(﹣ ,1)或 M(0,1).
【点评】本题为一次函数综合题,解题的关键是熟练掌握待定系数法求函数解析式、三角形
的面积公式,等腰三角形的性质等知识,其中(3)要注意分类求解,避免遗漏.
同课章节目录
