数学人教A版(2019)必修第一册4.3.1对数概念 课件(共21张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册4.3.1对数概念 课件(共21张ppt) |
|
|
| 格式 | pptx | ||
| 文件大小 | 588.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-10 20:49:36 | ||
图片预览

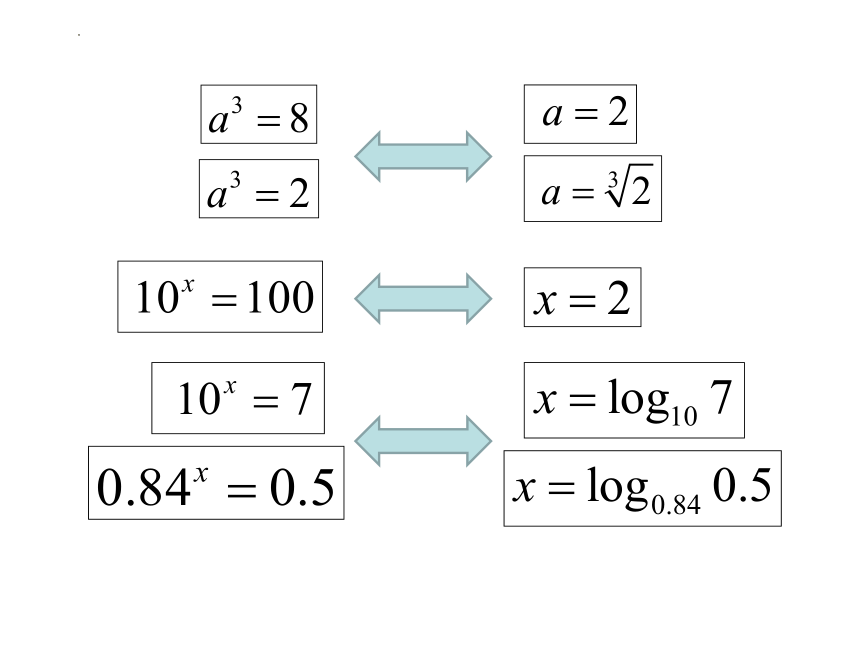





文档简介
(共21张PPT)
【问题情景】某种放射性物质不断变化为其他物质,每经过1年,
这种物质的剩留的质量是原来的84%,假设该物质最初的质量是1,请写出经过x年这种物质的剩留量y关于时间的函数关系式:
y=0.84x
由此,知道了经过的时间x,就能求出该物质的剩留量y;反过来,如果知道了y的值,怎样求出相应的x的值呢?
比如:当y=0.5时,相应的x的值是多少呢?
0.84x=0.5→x=
【思考】是否存在这样的实数x,使得 0.84x=0.5?
如果存在,x的值有几个?x等于多少呢?
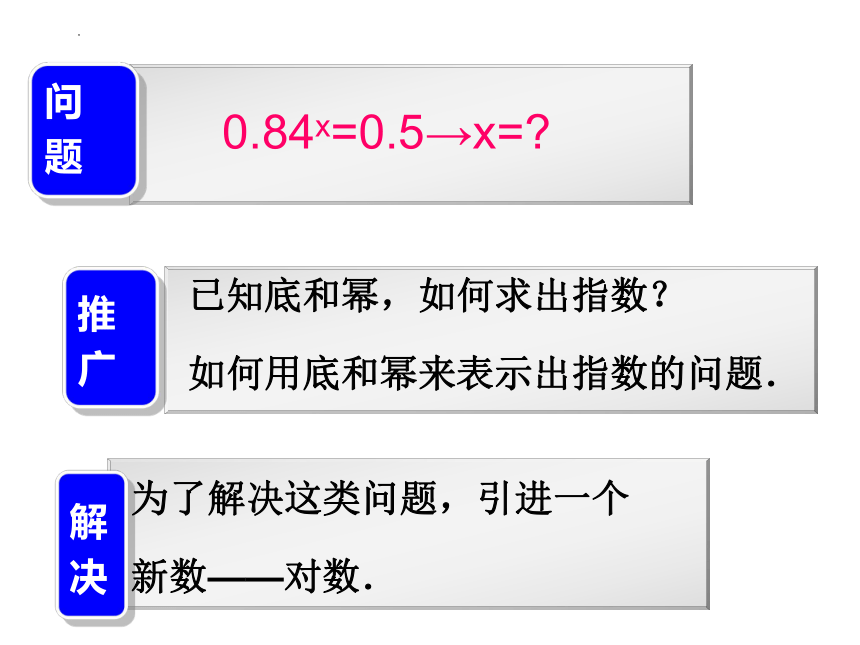
x
问
题
推
广
已知底和幂,如何求出指数?
如何用底和幂来表示出指数的问题.
解
决
为了解决这类问题,引进一个新数——对数.
0.84x=0.5→x=
对数的概念
1、对数的定义
叫做对数的底数, 叫做真数。
其中,
一般地,如果
的 次幂等于 , 即
为底 的对数,记作
那么就称 是以
对数(logarithm)
【注意】零和负数没有对数哟
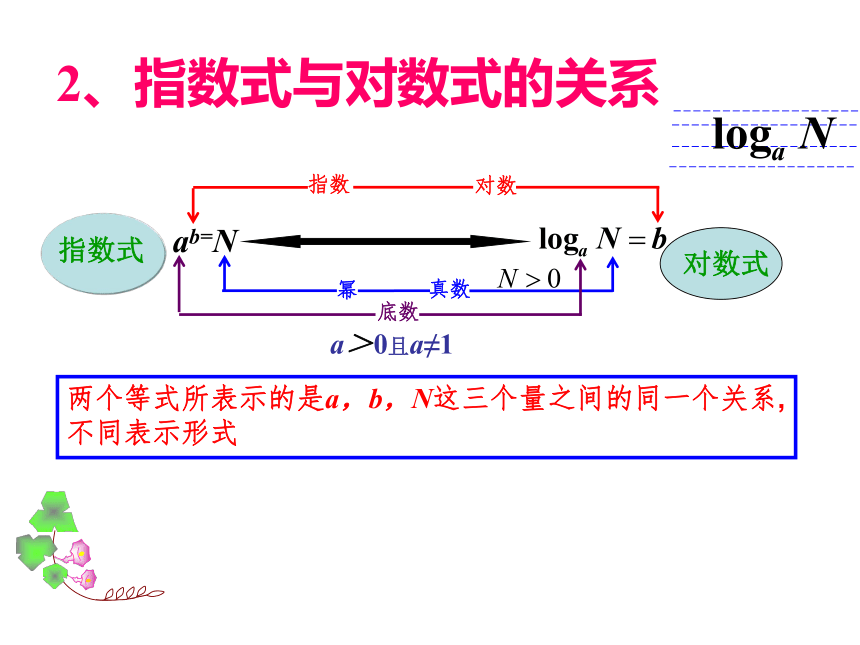
2、指数式与对数式的关系
ab=N
a>0且a≠1
两个等式所表示的是a,b,N这三个量之间的同一个关系,不同表示形式
指数
对数
幂
真数
底数
对数式
指数式
写作 读作 底数 真数
以2为底3的对数
2
3
以0.84为底0.5的对数
0.84
0.5
以 为底7的对数
7
指数式 对数式
例1.将下列指数式化成对数式
对数式 指数式
例2.将下列对数式化成指数式
常用对数:
我们通常将以10为底的对数叫做常用对数,
自然对数:
在科学技术中常常使用以无理数e=2.71828……
为底的对数,以e为底的对数叫自然对数.
为了简便,N的自然对数
简记作 .
为了简便,N的常用对数
简记作 .
3、两个特殊的对数:
求log(1-x)(x+2)中的x的取值范围.
练习:
例3 求出下列各式中 x 值:
解:(1)
解:(2)
例3 求出下列各式中 x 值:
【练习】求下列对数的值。
根据对数的定义,写出下列各对数的值
,
,
,
,
结论:
1的对数为0,
即 ,
底数的对数为1,
即 .
,
.
提炼一般性结论
0
1
思 考
探究活动:
探究:
loga1=0,logaa=1
练习:求下列各式x的值
解:
学生活动
计算探究
3
-4
6
3
2
提炼一般性结论
,
,
,
R
思考:
解:成立。此式为对数恒等式。
练习:求值
解:
多一份努力,得千分收获!
数学也励志
叫做指数式 ,
叫做对数式.
当
时,
底
底
指数
对数
幂
真数
指数式与对数式的互化
真数须正值不限,
底不为一且为正.
回顾小结
回顾小结
基本知识:
对数的定义,常用对数,对数的简单性质, 学会了对数
和指数的互化以及对数的简单计算.
思想方法:
归纳、猜想、证明等方法,类比思想、方程思想、
函数与方程思想、数形结合思想.
【问题情景】某种放射性物质不断变化为其他物质,每经过1年,
这种物质的剩留的质量是原来的84%,假设该物质最初的质量是1,请写出经过x年这种物质的剩留量y关于时间的函数关系式:
y=0.84x
由此,知道了经过的时间x,就能求出该物质的剩留量y;反过来,如果知道了y的值,怎样求出相应的x的值呢?
比如:当y=0.5时,相应的x的值是多少呢?
0.84x=0.5→x=
【思考】是否存在这样的实数x,使得 0.84x=0.5?
如果存在,x的值有几个?x等于多少呢?
x
问
题
推
广
已知底和幂,如何求出指数?
如何用底和幂来表示出指数的问题.
解
决
为了解决这类问题,引进一个新数——对数.
0.84x=0.5→x=
对数的概念
1、对数的定义
叫做对数的底数, 叫做真数。
其中,
一般地,如果
的 次幂等于 , 即
为底 的对数,记作
那么就称 是以
对数(logarithm)
【注意】零和负数没有对数哟
2、指数式与对数式的关系
ab=N
a>0且a≠1
两个等式所表示的是a,b,N这三个量之间的同一个关系,不同表示形式
指数
对数
幂
真数
底数
对数式
指数式
写作 读作 底数 真数
以2为底3的对数
2
3
以0.84为底0.5的对数
0.84
0.5
以 为底7的对数
7
指数式 对数式
例1.将下列指数式化成对数式
对数式 指数式
例2.将下列对数式化成指数式
常用对数:
我们通常将以10为底的对数叫做常用对数,
自然对数:
在科学技术中常常使用以无理数e=2.71828……
为底的对数,以e为底的对数叫自然对数.
为了简便,N的自然对数
简记作 .
为了简便,N的常用对数
简记作 .
3、两个特殊的对数:
求log(1-x)(x+2)中的x的取值范围.
练习:
例3 求出下列各式中 x 值:
解:(1)
解:(2)
例3 求出下列各式中 x 值:
【练习】求下列对数的值。
根据对数的定义,写出下列各对数的值
,
,
,
,
结论:
1的对数为0,
即 ,
底数的对数为1,
即 .
,
.
提炼一般性结论
0
1
思 考
探究活动:
探究:
loga1=0,logaa=1
练习:求下列各式x的值
解:
学生活动
计算探究
3
-4
6
3
2
提炼一般性结论
,
,
,
R
思考:
解:成立。此式为对数恒等式。
练习:求值
解:
多一份努力,得千分收获!
数学也励志
叫做指数式 ,
叫做对数式.
当
时,
底
底
指数
对数
幂
真数
指数式与对数式的互化
真数须正值不限,
底不为一且为正.
回顾小结
回顾小结
基本知识:
对数的定义,常用对数,对数的简单性质, 学会了对数
和指数的互化以及对数的简单计算.
思想方法:
归纳、猜想、证明等方法,类比思想、方程思想、
函数与方程思想、数形结合思想.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
