【苏科版】张家港市一中2014-2015学年度第二学期八年级数学下册9.3平行四边形导学案
文档属性
| 名称 | 【苏科版】张家港市一中2014-2015学年度第二学期八年级数学下册9.3平行四边形导学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 58.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-24 17:58:04 | ||
图片预览

文档简介
张家港市一中2014—2015学年度第二学期八年级数学导学案
初二 班 姓名 学号 主备人:王晓风
课题: 9.3平行四边形(1)
预学目标
1.动手实践课本P64的“操作”,初步感受平行四边形的中心对称性.
2.利用中心对称的性质初步了解平行四边形中相等的角和线段.
3.从边、角以及对角线三个方面尝试归纳平行四边形的性质.
知识梳理
l.平行四边形的概念
如图1,_______∥_______,_______∥_______,
则四边形ABCD是_______,记作_______,读作_______.
2.平行四边形是中心对称图形
观察图2,将△ABC绕AC边的中点O旋转180°,可得到△_____,
则△_____和△______关于点_______成_______对称,由性质可以得到
∠BAC=∠_____,∠BCA=∠_______,所以_______∥_______,
_____∥______,所以由概念可知四边形ABCD是平行四边形.
综上可知□ABCD是_______图形,对称中心是_______.
3.平行四边形的性质
如图2,由于□ABCD是中心对称图形,故由中心对称的性质可知:
(1) AB_______,AD_______,即_______________________________________;
(2)∠ABC=∠_______,∠BAD=∠_______,即______________________________;
(3) OA=_______,OB=_______,即________________________________________.
4.如图,在□ABCD中,
(l)若∠B=100°,则∠D=_______;
(2)若∠A+∠C=140°,则∠C=_______,∠B=_______;
(3)若AB:BC=3:4,周长为28 cm,则AD=_______ ,CD=_______;
(4)若□ABCD的周长为60 cm,对角线相交于点O,△AOB的周长比△BOC的周长少8 cm,则AB=_______,BC=_______.
例题精讲
(l)平行四边形ABCD的周长为80cm,相邻两边之比为1:3,则长边长
是_________cm,短边长是___________cm.
(2)在□ABCD中,∠A:∠B=1:2,则∠C=________,∠D=________.
(注意字母标写)
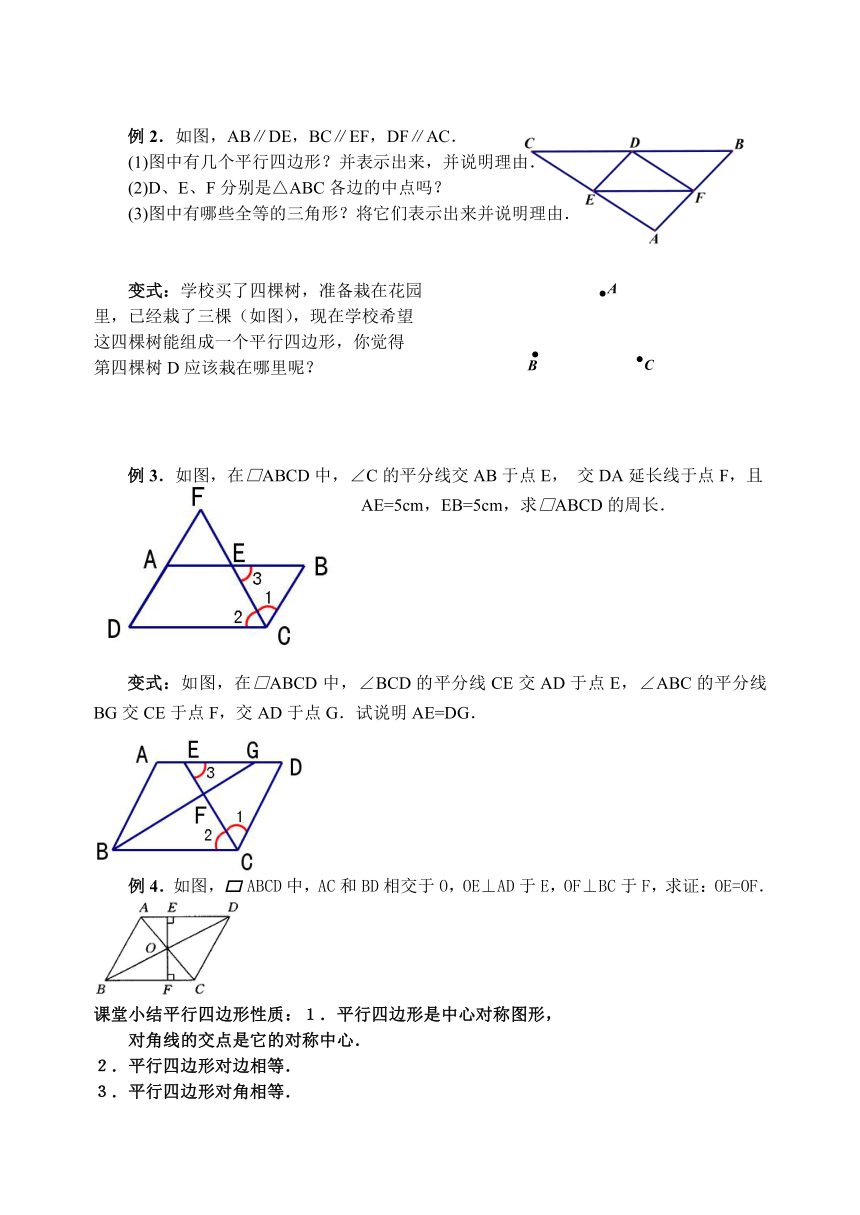
例2.如图,AB∥DE,BC∥EF,DF∥AC.
(1)图中有几个平行四边形?并表示出来,并说明理由.
(2)D、E、F分别是△ABC各边的中点吗?
(3)图中有哪些全等的三角形?将它们表示出来并说明理由.
变式:学校买了四棵树,准备栽在花园
里,已经栽了三棵(如图),现在学校希望
这四棵树能组成一个平行四边形,你觉得
第四棵树D应该栽在哪里呢?
例3.如图,在□ABCD中,∠C的平分线交AB于点E, 交DA延长线于点F,且AE=5cm,EB=5cm,求□ABCD的周长.
变式:如图,在□ABCD中,∠BCD的平分线CE交AD于点E,∠ABC的平分线BG交CE于点F,交AD于点G.试说明AE=DG.
例4.如图,ABCD中,AC和BD相交于O,OE⊥AD于E,OF⊥BC于F,求证:OE=OF.
课堂小结平行四边形性质:1.平行四边形是中心对称图形,
对角线的交点是它的对称中心.
2.平行四边形对边相等.
3.平行四边形对角相等.
4.平行四边形的对角线互相平分.
添加:这节课涉及到的数学思想:
转化思想
整体思想
方程思想
数形结合思想
教后小记:本节课学习平行四边形的概念与性质及其运用,在学生的预习过程中,让学生初步掌握基础知识和基本运算,课堂上通过学生自主探索和动手操作加上合作交流,鼓励学生主动上台讲解,在解题过程中,与学生一起探讨解题的方法,灌输总结数学的思想方法和解题技巧。
初二数学课堂练习 班级 姓名 学号
1.在□ABCD中,AB=5 cm,BC=4 cm,则□ABCD的周长为_______.
2.在□ABCD中,如果∠B=100°,那么∠A、∠D的度数分别是 ( )
A.∠A=80°、∠D=100° B.∠A=100°、∠D=80°
C.∠B=80°、∠D=80° D.∠A=100°、∠D=100°
3.如图,在□ABCD中,∠ABD=90°,∠ADB=30°,
则四个内角的度数分别为_______°、_______°、_______°、_______°.
4.平行四边形的周长等于56 cm,两邻边长的比为3:1,
那么这个平行四边形较长边的长为_______.
5.如图,在□ABCD中,AD=8 cm,AB=6 cm,DE
平分∠ADC,交BC边于点E,则BE的长为 ( )
A.2 cm B.4 cm C.6 cm D.8 cm
6.如图,在□ABCD中,AC、BD为对角线,BC=6,
BC边上的高为4,则阴影部分的面积为 ( )
A.3 B.6 C.12 D.24
7.如果□ABCD的周长为40 cm,△ABC的周长为25 cm,则对角线AC的长是 ( )
A.5 cm B.15 cm C.6 cm D.16 cm
8.在□ABCD中,AC、BD相交于点O,则图中共有全等三角形( )
A.1对 B.2对 C.3对 D.4对
9.如图,E是□ABCD的边AD的中点,CE与BA的延长线交于点F,若∠FCD=∠D,则下列结论不成立的是 ( )
A.AD=CF B.BF=CF C.AF=CD D.DE=EF
10.在□ABCD中,对角线AC与BD相交于O,若AC=6,BD=10则AD长度x的取值范围是 A.211.如图,E、F是□ABCD对角线AC上的两点,BE∥DF.求证:AF=CE.
12.如图,□ABCD的边BC上有一点E,且AE=AD,AE、DC的延长线相交于点F,
∠ADE=55°,那么∠CEF的度数是多少?
13.如图,在□ABCD中,EF过对角线的交点O,若AD=8cm,AB=6cm,OE=4cm,
求四边形ABFE的周长.
14.如图,在□ABCD中,AE⊥BC于点E,AF⊥CD于点F,若AE=4,AF=6,
□ABCD的周长为40,则□ABCD的面积为多少
15.如图,在□ABCD中,∠ABC=60°,E、F分别在CD、BC的延长线上,AE∥BD,EF⊥BC,DF=2,求EF的长.
16.用三种不同的方法把□ABCD的面积四等分,并简要说明分法.
A
C
B
初二 班 姓名 学号 主备人:王晓风
课题: 9.3平行四边形(1)
预学目标
1.动手实践课本P64的“操作”,初步感受平行四边形的中心对称性.
2.利用中心对称的性质初步了解平行四边形中相等的角和线段.
3.从边、角以及对角线三个方面尝试归纳平行四边形的性质.
知识梳理
l.平行四边形的概念
如图1,_______∥_______,_______∥_______,
则四边形ABCD是_______,记作_______,读作_______.
2.平行四边形是中心对称图形
观察图2,将△ABC绕AC边的中点O旋转180°,可得到△_____,
则△_____和△______关于点_______成_______对称,由性质可以得到
∠BAC=∠_____,∠BCA=∠_______,所以_______∥_______,
_____∥______,所以由概念可知四边形ABCD是平行四边形.
综上可知□ABCD是_______图形,对称中心是_______.
3.平行四边形的性质
如图2,由于□ABCD是中心对称图形,故由中心对称的性质可知:
(1) AB_______,AD_______,即_______________________________________;
(2)∠ABC=∠_______,∠BAD=∠_______,即______________________________;
(3) OA=_______,OB=_______,即________________________________________.
4.如图,在□ABCD中,
(l)若∠B=100°,则∠D=_______;
(2)若∠A+∠C=140°,则∠C=_______,∠B=_______;
(3)若AB:BC=3:4,周长为28 cm,则AD=_______ ,CD=_______;
(4)若□ABCD的周长为60 cm,对角线相交于点O,△AOB的周长比△BOC的周长少8 cm,则AB=_______,BC=_______.
例题精讲
(l)平行四边形ABCD的周长为80cm,相邻两边之比为1:3,则长边长
是_________cm,短边长是___________cm.
(2)在□ABCD中,∠A:∠B=1:2,则∠C=________,∠D=________.
(注意字母标写)
例2.如图,AB∥DE,BC∥EF,DF∥AC.
(1)图中有几个平行四边形?并表示出来,并说明理由.
(2)D、E、F分别是△ABC各边的中点吗?
(3)图中有哪些全等的三角形?将它们表示出来并说明理由.
变式:学校买了四棵树,准备栽在花园
里,已经栽了三棵(如图),现在学校希望
这四棵树能组成一个平行四边形,你觉得
第四棵树D应该栽在哪里呢?
例3.如图,在□ABCD中,∠C的平分线交AB于点E, 交DA延长线于点F,且AE=5cm,EB=5cm,求□ABCD的周长.
变式:如图,在□ABCD中,∠BCD的平分线CE交AD于点E,∠ABC的平分线BG交CE于点F,交AD于点G.试说明AE=DG.
例4.如图,ABCD中,AC和BD相交于O,OE⊥AD于E,OF⊥BC于F,求证:OE=OF.
课堂小结平行四边形性质:1.平行四边形是中心对称图形,
对角线的交点是它的对称中心.
2.平行四边形对边相等.
3.平行四边形对角相等.
4.平行四边形的对角线互相平分.
添加:这节课涉及到的数学思想:
转化思想
整体思想
方程思想
数形结合思想
教后小记:本节课学习平行四边形的概念与性质及其运用,在学生的预习过程中,让学生初步掌握基础知识和基本运算,课堂上通过学生自主探索和动手操作加上合作交流,鼓励学生主动上台讲解,在解题过程中,与学生一起探讨解题的方法,灌输总结数学的思想方法和解题技巧。
初二数学课堂练习 班级 姓名 学号
1.在□ABCD中,AB=5 cm,BC=4 cm,则□ABCD的周长为_______.
2.在□ABCD中,如果∠B=100°,那么∠A、∠D的度数分别是 ( )
A.∠A=80°、∠D=100° B.∠A=100°、∠D=80°
C.∠B=80°、∠D=80° D.∠A=100°、∠D=100°
3.如图,在□ABCD中,∠ABD=90°,∠ADB=30°,
则四个内角的度数分别为_______°、_______°、_______°、_______°.
4.平行四边形的周长等于56 cm,两邻边长的比为3:1,
那么这个平行四边形较长边的长为_______.
5.如图,在□ABCD中,AD=8 cm,AB=6 cm,DE
平分∠ADC,交BC边于点E,则BE的长为 ( )
A.2 cm B.4 cm C.6 cm D.8 cm
6.如图,在□ABCD中,AC、BD为对角线,BC=6,
BC边上的高为4,则阴影部分的面积为 ( )
A.3 B.6 C.12 D.24
7.如果□ABCD的周长为40 cm,△ABC的周长为25 cm,则对角线AC的长是 ( )
A.5 cm B.15 cm C.6 cm D.16 cm
8.在□ABCD中,AC、BD相交于点O,则图中共有全等三角形( )
A.1对 B.2对 C.3对 D.4对
9.如图,E是□ABCD的边AD的中点,CE与BA的延长线交于点F,若∠FCD=∠D,则下列结论不成立的是 ( )
A.AD=CF B.BF=CF C.AF=CD D.DE=EF
10.在□ABCD中,对角线AC与BD相交于O,若AC=6,BD=10则AD长度x的取值范围是 A.2
12.如图,□ABCD的边BC上有一点E,且AE=AD,AE、DC的延长线相交于点F,
∠ADE=55°,那么∠CEF的度数是多少?
13.如图,在□ABCD中,EF过对角线的交点O,若AD=8cm,AB=6cm,OE=4cm,
求四边形ABFE的周长.
14.如图,在□ABCD中,AE⊥BC于点E,AF⊥CD于点F,若AE=4,AF=6,
□ABCD的周长为40,则□ABCD的面积为多少
15.如图,在□ABCD中,∠ABC=60°,E、F分别在CD、BC的延长线上,AE∥BD,EF⊥BC,DF=2,求EF的长.
16.用三种不同的方法把□ABCD的面积四等分,并简要说明分法.
A
C
B
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
