2023—2024学年苏科版数学九年级上册2.2圆的对称性 垂径定理 讲义(表格式 无答案)
文档属性
| 名称 | 2023—2024学年苏科版数学九年级上册2.2圆的对称性 垂径定理 讲义(表格式 无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 443.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-12 00:00:00 | ||
图片预览



文档简介
2.2圆的对称性
(垂径定理)
教学目的 掌握垂径定理; 掌握垂径定理的推论重点难点利用垂径定理求圆的半径或直径; 利用垂径定理求圆相关的角度或长度; 利用垂径定理求实际问题中的解
知识梳理
【知识点一】垂径定理 1.定义:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧. 2.推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧. 平分弦(该弦不是直径)的直径垂直于弦,并且平分弦所对的两条弧; 弦的垂直平分线经过圆心,并且平分弦所对的两条弧; 平分弦所对的一条弧的直径,垂直平分线,并且平分弦所对的另一条弧.
典型例题讲解
【例1】下列语句中,正确的有( ) (1)相等的圆心角所对的弧相等; (2)平分弦的直径垂直于弦; (3)长度相等的两条弧是等弧; (4)圆是轴对称图形,任何一条直径都是对称轴. A.0个 B.1个 C.2个 D.3个 【例2】如图,已知⊙O的直径AB⊥CD弦于点E,则下列结论不一定成立的是( ) A.CE=DE B.AE=OE C.∠COA=∠DOA D.△OCE≌△ODE 【例3】筒车是我国古代发明的一种水利灌溉工具,如图1,筒车盛水桶的运行轨道是以轴心为圆心的圆,如图2,已知圆心在水面上方,且被水面截得弦长为4米,半径长为3米.若点为运行轨道的最低点,则点到弦所在直线的距离是 A.1米 B.2米 C.米 D.米 【例4】已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图). 求证:AC=BD.
举一反三
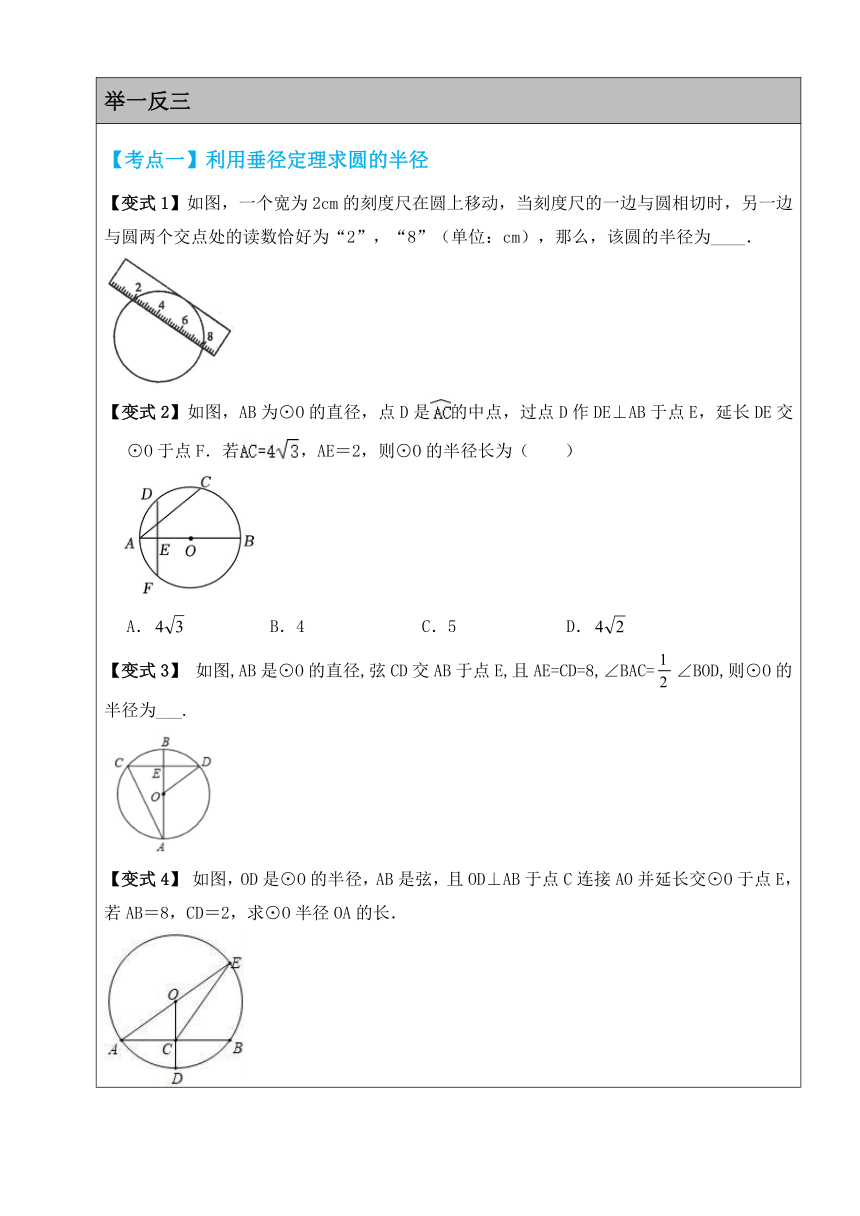
【考点一】利用垂径定理求圆的半径 【变式1】如图,一个宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”,“8”(单位:cm),那么,该圆的半径为____. 【变式2】如图,AB为⊙O的直径,点D是的中点,过点D作DE⊥AB于点E,延长DE交⊙O于点F.若,AE=2,则⊙O的半径长为( ) A. B.4 C.5 D. 【变式3】 如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BAC=∠BOD,则⊙O的半径为___. 【变式4】 如图,OD是⊙O的半径,AB是弦,且OD⊥AB于点C连接AO并延长交⊙O于点E,若AB=8,CD=2,求⊙O半径OA的长. 【考点二】利用垂径定理求线段长度 【变式1】如图,在半径为的⊙O中,弦AB,CD互相垂直,垂足为点P.若AB=CD=8,则OP的长为( ) A. B. C.4 D.2 【变式2】如图:AB是⊙O的直径,弦CD⊥AB于E,若AB=20,CD=16,则线段BE的长为( ) A.4 B.6 C.8 D.10 【变式3】 如图,圆O的半径OD垂直弦AB于点C,连接AO并延长交圆O于点E,连接BE.若AB=8,BE=6,则CD长为( ) A.2 B.2.5 C.3 D.4 【变式4】如图,A、B、C是⊙O上的点,OC⊥AB,垂足为点D,且D为OC的中点,若OA=7,则BC的长为 . 【考点三】垂径定理的实际应用 【变式1】如图,武汉晴川桥可以近似地看作半径为250m的圆弧,桥拱和路面之间用数根钢索垂直相连,其正下方的路面AB长度为300m,那么这些钢索中最长的一根为( ) A.50m B.45m C.40m D.60m 【变式2】如图是一座圆弧型拱桥的截面示意图,若桥面跨度米,拱高米为的中点,为弧的中点).则桥拱所在圆的半径为 米. 【变式3】 随着疫情的持续,各地政府储存了充足的防疫物品.某防疫物品储藏室的截面是由如图所示的图形构成的,图形下面是长方形ABCD,上面是半圆形,其中AB=2.3m,BC=2.6m,一辆装满货物的运输车,其外形高2.6m,宽2.4m,它能通过储藏室的门吗?请说明理由. 【变式4】 在半径为的圆柱形油罐内装进一些油后,横截面如图. ①若油面宽,求油的最大深度. ②在①的条件下,若油面宽变为,求油的最大深度上升了多少?
小试牛刀
1.下列说法中错误的有( )
①过弦的中点的直线平分弦所对的两条弧;
②弦的垂线平分它所对的两条弧;
③过弦的中点的直径平分弦所对的两条弧;
④平分不是直径的弦的直径平分弦所对的两条弧. A.1个 B.2个 C.3个 D.4个 2.如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5,CD=8,则OE=( ) A.5 B.4 C.3 D.2 3.如图,是的中点,弦,,且,则所在圆的半径为 A.4 B.5 C.6 D.10 4.如图,⊙O的半径为10,弦AB=16,M是弦AB上的动点,则OM不可能为( ) A.5 B.6 C.7 D.8 5.点P是⊙O内一点,过点P的最长弦的长为10cm,最短弦的长为6cm,则OP的长为 . 6.如图,⊙O与矩形ABCD的边AB、CD分别相交于点E、F、G、H,若AE+CH=6,则BG+DF为 . 7.石拱桥是中国传统桥梁四大基本形式之一,如图,已知一石拱桥的桥顶到水面的距离CD为8m,桥拱半径OC为5m,求水面宽AB= m. 8.如图,在平面直角坐标系中,点O为坐标原点,点P在第一象限,⊙P与x轴交于O,A两点,点A的坐标为(6,0),⊙P的半径为,则点P的坐标为_______. 9.如图,有一座拱桥是圆弧形,它的跨度米,拱高米. (1)求圆弧所在的圆的半径的长; (2)当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即米时,是否要采取紧急措施? 10.如图,一条公路的转弯处是一段圆弧AB,点O是弧AB的圆心,C为弧AB上一点,OC⊥AB,垂足为D.已知AB=60m,CD=10m,求这段弯路的半径.
(垂径定理)
教学目的 掌握垂径定理; 掌握垂径定理的推论重点难点利用垂径定理求圆的半径或直径; 利用垂径定理求圆相关的角度或长度; 利用垂径定理求实际问题中的解
知识梳理
【知识点一】垂径定理 1.定义:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧. 2.推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧. 平分弦(该弦不是直径)的直径垂直于弦,并且平分弦所对的两条弧; 弦的垂直平分线经过圆心,并且平分弦所对的两条弧; 平分弦所对的一条弧的直径,垂直平分线,并且平分弦所对的另一条弧.
典型例题讲解
【例1】下列语句中,正确的有( ) (1)相等的圆心角所对的弧相等; (2)平分弦的直径垂直于弦; (3)长度相等的两条弧是等弧; (4)圆是轴对称图形,任何一条直径都是对称轴. A.0个 B.1个 C.2个 D.3个 【例2】如图,已知⊙O的直径AB⊥CD弦于点E,则下列结论不一定成立的是( ) A.CE=DE B.AE=OE C.∠COA=∠DOA D.△OCE≌△ODE 【例3】筒车是我国古代发明的一种水利灌溉工具,如图1,筒车盛水桶的运行轨道是以轴心为圆心的圆,如图2,已知圆心在水面上方,且被水面截得弦长为4米,半径长为3米.若点为运行轨道的最低点,则点到弦所在直线的距离是 A.1米 B.2米 C.米 D.米 【例4】已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图). 求证:AC=BD.
举一反三
【考点一】利用垂径定理求圆的半径 【变式1】如图,一个宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”,“8”(单位:cm),那么,该圆的半径为____. 【变式2】如图,AB为⊙O的直径,点D是的中点,过点D作DE⊥AB于点E,延长DE交⊙O于点F.若,AE=2,则⊙O的半径长为( ) A. B.4 C.5 D. 【变式3】 如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BAC=∠BOD,则⊙O的半径为___. 【变式4】 如图,OD是⊙O的半径,AB是弦,且OD⊥AB于点C连接AO并延长交⊙O于点E,若AB=8,CD=2,求⊙O半径OA的长. 【考点二】利用垂径定理求线段长度 【变式1】如图,在半径为的⊙O中,弦AB,CD互相垂直,垂足为点P.若AB=CD=8,则OP的长为( ) A. B. C.4 D.2 【变式2】如图:AB是⊙O的直径,弦CD⊥AB于E,若AB=20,CD=16,则线段BE的长为( ) A.4 B.6 C.8 D.10 【变式3】 如图,圆O的半径OD垂直弦AB于点C,连接AO并延长交圆O于点E,连接BE.若AB=8,BE=6,则CD长为( ) A.2 B.2.5 C.3 D.4 【变式4】如图,A、B、C是⊙O上的点,OC⊥AB,垂足为点D,且D为OC的中点,若OA=7,则BC的长为 . 【考点三】垂径定理的实际应用 【变式1】如图,武汉晴川桥可以近似地看作半径为250m的圆弧,桥拱和路面之间用数根钢索垂直相连,其正下方的路面AB长度为300m,那么这些钢索中最长的一根为( ) A.50m B.45m C.40m D.60m 【变式2】如图是一座圆弧型拱桥的截面示意图,若桥面跨度米,拱高米为的中点,为弧的中点).则桥拱所在圆的半径为 米. 【变式3】 随着疫情的持续,各地政府储存了充足的防疫物品.某防疫物品储藏室的截面是由如图所示的图形构成的,图形下面是长方形ABCD,上面是半圆形,其中AB=2.3m,BC=2.6m,一辆装满货物的运输车,其外形高2.6m,宽2.4m,它能通过储藏室的门吗?请说明理由. 【变式4】 在半径为的圆柱形油罐内装进一些油后,横截面如图. ①若油面宽,求油的最大深度. ②在①的条件下,若油面宽变为,求油的最大深度上升了多少?
小试牛刀
1.下列说法中错误的有( )
①过弦的中点的直线平分弦所对的两条弧;
②弦的垂线平分它所对的两条弧;
③过弦的中点的直径平分弦所对的两条弧;
④平分不是直径的弦的直径平分弦所对的两条弧. A.1个 B.2个 C.3个 D.4个 2.如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5,CD=8,则OE=( ) A.5 B.4 C.3 D.2 3.如图,是的中点,弦,,且,则所在圆的半径为 A.4 B.5 C.6 D.10 4.如图,⊙O的半径为10,弦AB=16,M是弦AB上的动点,则OM不可能为( ) A.5 B.6 C.7 D.8 5.点P是⊙O内一点,过点P的最长弦的长为10cm,最短弦的长为6cm,则OP的长为 . 6.如图,⊙O与矩形ABCD的边AB、CD分别相交于点E、F、G、H,若AE+CH=6,则BG+DF为 . 7.石拱桥是中国传统桥梁四大基本形式之一,如图,已知一石拱桥的桥顶到水面的距离CD为8m,桥拱半径OC为5m,求水面宽AB= m. 8.如图,在平面直角坐标系中,点O为坐标原点,点P在第一象限,⊙P与x轴交于O,A两点,点A的坐标为(6,0),⊙P的半径为,则点P的坐标为_______. 9.如图,有一座拱桥是圆弧形,它的跨度米,拱高米. (1)求圆弧所在的圆的半径的长; (2)当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即米时,是否要采取紧急措施? 10.如图,一条公路的转弯处是一段圆弧AB,点O是弧AB的圆心,C为弧AB上一点,OC⊥AB,垂足为D.已知AB=60m,CD=10m,求这段弯路的半径.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
