2023—2024学年苏科版数学九年级上册2.6正多边形与圆 讲义(表格式 无答案)
文档属性
| 名称 | 2023—2024学年苏科版数学九年级上册2.6正多边形与圆 讲义(表格式 无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 877.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-12 18:23:10 | ||
图片预览


文档简介
2.6正多边形与圆
教学目的 掌握正多边形的外接圆的定义与性质; 掌握正多边形相关的计算公式 重点难点利用正多边形的外接圆的性质求相关的角度、线段等; 掌握求正多边形的边数;
知识梳理
【知识点一】正多边形与圆
1.正多边形的有关概念
(1)一个正多边形的外接圆的圆心叫做这个正多边形的中心.
(2)正多边形外接圆的半径叫做正多边形的半径.
(3)正多边形每一边所对的圆心角叫做正多边形的中心角.
(4)正多边形的中心到正多边形的一边的距离叫做正多边形的边心距.
2.正多边形的有关计算
(1)正n边形每一个内角的度数是;
(2)正n边形每个中心角的度数是;
(3)正n边形每个外角的度数是.
典型例题讲解
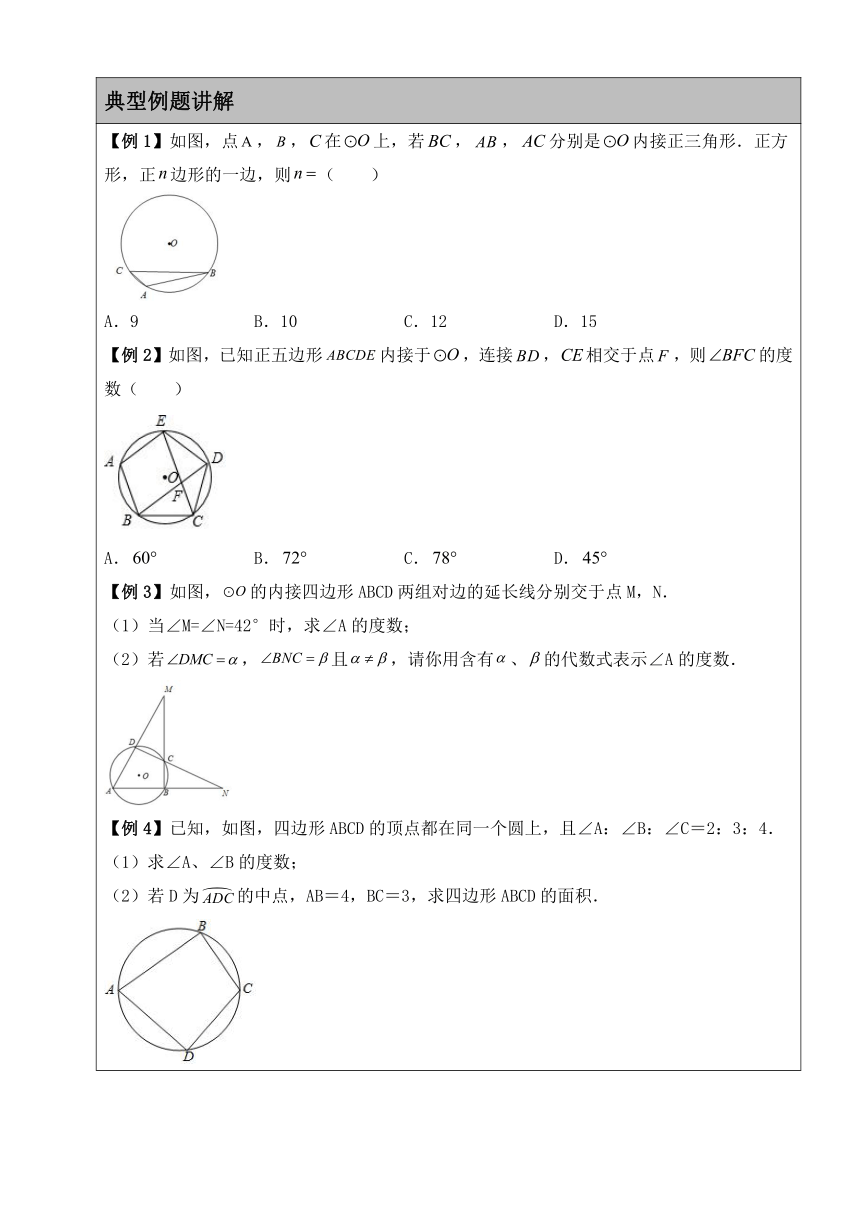
【例1】如图,点,,在上,若,,分别是内接正三角形.正方形,正边形的一边,则( ) A.9 B.10 C.12 D.15 【例2】如图,已知正五边形内接于,连接,相交于点,则的度数( ) A. B. C. D. 【例3】如图,的内接四边形ABCD两组对边的延长线分别交于点M,N. (1)当∠M=∠N=42°时,求∠A的度数; (2)若,且,请你用含有、的代数式表示∠A的度数. 【例4】已知,如图,四边形ABCD的顶点都在同一个圆上,且∠A:∠B:∠C=2:3:4. (1)求∠A、∠B的度数; (2)若D为的中点,AB=4,BC=3,求四边形ABCD的面积.
举一反三
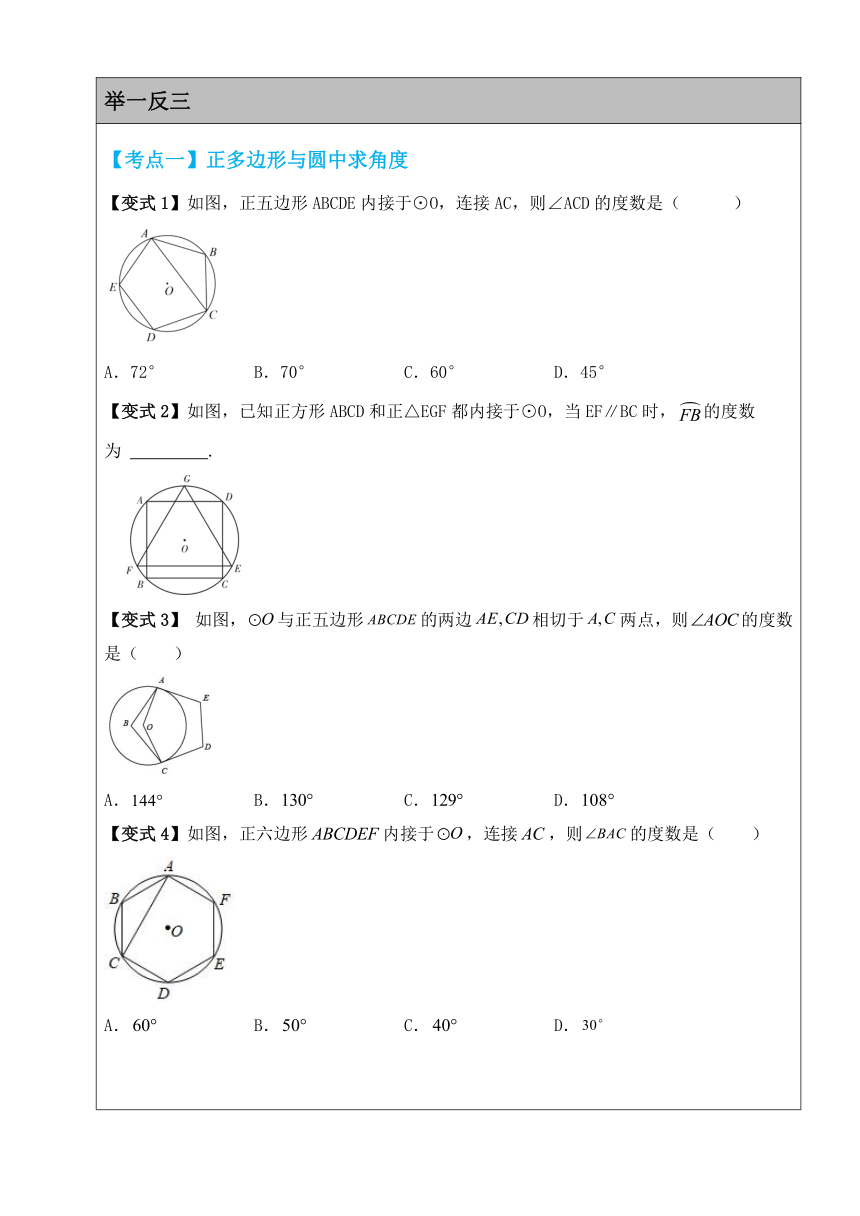
【考点一】正多边形与圆中求角度 【变式1】如图,正五边形ABCDE内接于⊙O,连接AC,则∠ACD的度数是( ) A.72° B.70° C.60° D.45° 【变式2】如图,已知正方形ABCD和正△EGF都内接于⊙O,当EF∥BC时,的度数为 . 【变式3】 如图,与正五边形的两边相切于两点,则的度数是( ) A. B. C. D. 【变式4】如图,正六边形内接于,连接,则的度数是( ) A. B. C. D. 【考点二】求正多边形的边数 【变式1】如图,A,B,C,D为一个正多边形的顶点,O为正多边形的中心,若∠ADB=18°,则这个正多边形的边数为 . 【变式2】如图,边AB是⊙O内接正六边形的一边,点C在弧AB上,且BC是⊙O内接正八边形的一边,若AC是⊙O内接正n边形的一边,则n的值是( ) A.6 B.12 C.24 D.48 【变式3】 如图,AB、AC分别为⊙O的内接正方形、内接正三边形的边,BC是圆内接正n边形的一边,则n等于( ) A.8 B.10 C.12 D.16 【变式4】 如图,四边形ABCD为⊙O的内接正四边形,△AEF为⊙O的内接正三角形,若DF恰好是同圆的一个内接正n边形的一边,则n的值为( ) A.8 B.10 C.12 D.15 【考点三】内接多边形的证明 【变式1】已知,如图,△ABC内接于⊙O,AB=AC,∠BAC=36°,AB、AC的中垂线分别交⊙O于点E、F,证明:五边形AEBCF是⊙O的内接正五边形. 【变式2】如图,四边形内接于圆,,对角线平分. (1)求证:是等边三角形; (2)过点作交的延长线于点,若,求的面积. 【变式3】如图,⊙O半径为4cm,其内接正六边形ABCDEF,点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向终点F,C运动,连接PB,QE,PE,BQ.设运动时间为t(s). (1)求证:四边形PEQB为平行四边形; (2)填空: ①当t= s时,四边形PBQE为菱形; ②当t= s时,四边形PBQE为矩形. 【变式4】 如图1,正五边形内接于⊙,阅读以下作图过程,并回答下列问题,作法:如图2,①作直径;②以F为圆心,为半径作圆弧,与⊙交于点M,N;③连接. (1) 求的度数. (2) 是正三角形吗?请说明理由. (3) 从点A开始,以长为半径,在⊙上依次截取点,再依次连接这些分点,得到正n边形,求n的值.
小试牛刀
1.若正方形的外接圆半径为2,则其边长为( ) A. B.2 C. D.1 2.如图所示,为的内接三角形,,则的内接正方形的面积( ) A. B. C. D. 3.大自然中有许多小动物都是“小数学家”,如图1,蜜蜂的蜂巢结构非常精巧、实用而且节省材料,多名学者通过观测研究发现:蜂巢巢房的横截面大都是正六边形.如图2,一个巢房的横截面为正六边形,若对角线的长约为8mm,则正六边形的边长为( ) A.2mm B. C. D.4mm 4.如图,正五边形和正三角形都是的内接多边形,则的度数是( ) A. B. C. D. 5.如图,正六边形ABCDEF内接于⊙O,连接OC、OD,若OC长为2cm,则正六形ABCDEF的周长为______cm. 6.如图,正五边形ABCDE内接于⊙O,点P是劣弧上一点(点P不与点C重合),则∠CPD=________. 7.如图,圆的半径为4,则图中阴影部分的周长是________. 8.如图,△ABC为⊙O的内接等边三角形,BC=12,点D为上一动点,BE⊥OD于E,当点D由点B沿运动到点C时,线段AE的最大值是____. 9.如图,正方形内接于,为上的一点,连接,. (1)求的度数; (2)当点为的中点时,是的内接正边形的一边,求的值. 10.如图①、②、③,正三角形ABC、正方形ABCD、正五边形ABCDE分别是⊙O的内接三角形、内接四边形、内接五边形,点M、N分别从点B、C开始,以相同的速度中⊙O上逆时针运动. (1)求图①中∠APB的度数; (2)图②中,∠APB的度数是 90°,图③中∠APB的度数是 72°; (3)根据前面探索,你能否将本题推广到一般的正n边形情况?若能,写出推广问题和结论;若不能,请说明理由.
教学目的 掌握正多边形的外接圆的定义与性质; 掌握正多边形相关的计算公式 重点难点利用正多边形的外接圆的性质求相关的角度、线段等; 掌握求正多边形的边数;
知识梳理
【知识点一】正多边形与圆
1.正多边形的有关概念
(1)一个正多边形的外接圆的圆心叫做这个正多边形的中心.
(2)正多边形外接圆的半径叫做正多边形的半径.
(3)正多边形每一边所对的圆心角叫做正多边形的中心角.
(4)正多边形的中心到正多边形的一边的距离叫做正多边形的边心距.
2.正多边形的有关计算
(1)正n边形每一个内角的度数是;
(2)正n边形每个中心角的度数是;
(3)正n边形每个外角的度数是.
典型例题讲解
【例1】如图,点,,在上,若,,分别是内接正三角形.正方形,正边形的一边,则( ) A.9 B.10 C.12 D.15 【例2】如图,已知正五边形内接于,连接,相交于点,则的度数( ) A. B. C. D. 【例3】如图,的内接四边形ABCD两组对边的延长线分别交于点M,N. (1)当∠M=∠N=42°时,求∠A的度数; (2)若,且,请你用含有、的代数式表示∠A的度数. 【例4】已知,如图,四边形ABCD的顶点都在同一个圆上,且∠A:∠B:∠C=2:3:4. (1)求∠A、∠B的度数; (2)若D为的中点,AB=4,BC=3,求四边形ABCD的面积.
举一反三
【考点一】正多边形与圆中求角度 【变式1】如图,正五边形ABCDE内接于⊙O,连接AC,则∠ACD的度数是( ) A.72° B.70° C.60° D.45° 【变式2】如图,已知正方形ABCD和正△EGF都内接于⊙O,当EF∥BC时,的度数为 . 【变式3】 如图,与正五边形的两边相切于两点,则的度数是( ) A. B. C. D. 【变式4】如图,正六边形内接于,连接,则的度数是( ) A. B. C. D. 【考点二】求正多边形的边数 【变式1】如图,A,B,C,D为一个正多边形的顶点,O为正多边形的中心,若∠ADB=18°,则这个正多边形的边数为 . 【变式2】如图,边AB是⊙O内接正六边形的一边,点C在弧AB上,且BC是⊙O内接正八边形的一边,若AC是⊙O内接正n边形的一边,则n的值是( ) A.6 B.12 C.24 D.48 【变式3】 如图,AB、AC分别为⊙O的内接正方形、内接正三边形的边,BC是圆内接正n边形的一边,则n等于( ) A.8 B.10 C.12 D.16 【变式4】 如图,四边形ABCD为⊙O的内接正四边形,△AEF为⊙O的内接正三角形,若DF恰好是同圆的一个内接正n边形的一边,则n的值为( ) A.8 B.10 C.12 D.15 【考点三】内接多边形的证明 【变式1】已知,如图,△ABC内接于⊙O,AB=AC,∠BAC=36°,AB、AC的中垂线分别交⊙O于点E、F,证明:五边形AEBCF是⊙O的内接正五边形. 【变式2】如图,四边形内接于圆,,对角线平分. (1)求证:是等边三角形; (2)过点作交的延长线于点,若,求的面积. 【变式3】如图,⊙O半径为4cm,其内接正六边形ABCDEF,点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向终点F,C运动,连接PB,QE,PE,BQ.设运动时间为t(s). (1)求证:四边形PEQB为平行四边形; (2)填空: ①当t= s时,四边形PBQE为菱形; ②当t= s时,四边形PBQE为矩形. 【变式4】 如图1,正五边形内接于⊙,阅读以下作图过程,并回答下列问题,作法:如图2,①作直径;②以F为圆心,为半径作圆弧,与⊙交于点M,N;③连接. (1) 求的度数. (2) 是正三角形吗?请说明理由. (3) 从点A开始,以长为半径,在⊙上依次截取点,再依次连接这些分点,得到正n边形,求n的值.
小试牛刀
1.若正方形的外接圆半径为2,则其边长为( ) A. B.2 C. D.1 2.如图所示,为的内接三角形,,则的内接正方形的面积( ) A. B. C. D. 3.大自然中有许多小动物都是“小数学家”,如图1,蜜蜂的蜂巢结构非常精巧、实用而且节省材料,多名学者通过观测研究发现:蜂巢巢房的横截面大都是正六边形.如图2,一个巢房的横截面为正六边形,若对角线的长约为8mm,则正六边形的边长为( ) A.2mm B. C. D.4mm 4.如图,正五边形和正三角形都是的内接多边形,则的度数是( ) A. B. C. D. 5.如图,正六边形ABCDEF内接于⊙O,连接OC、OD,若OC长为2cm,则正六形ABCDEF的周长为______cm. 6.如图,正五边形ABCDE内接于⊙O,点P是劣弧上一点(点P不与点C重合),则∠CPD=________. 7.如图,圆的半径为4,则图中阴影部分的周长是________. 8.如图,△ABC为⊙O的内接等边三角形,BC=12,点D为上一动点,BE⊥OD于E,当点D由点B沿运动到点C时,线段AE的最大值是____. 9.如图,正方形内接于,为上的一点,连接,. (1)求的度数; (2)当点为的中点时,是的内接正边形的一边,求的值. 10.如图①、②、③,正三角形ABC、正方形ABCD、正五边形ABCDE分别是⊙O的内接三角形、内接四边形、内接五边形,点M、N分别从点B、C开始,以相同的速度中⊙O上逆时针运动. (1)求图①中∠APB的度数; (2)图②中,∠APB的度数是 90°,图③中∠APB的度数是 72°; (3)根据前面探索,你能否将本题推广到一般的正n边形情况?若能,写出推广问题和结论;若不能,请说明理由.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
