人教版六年级数学下册第5单元《鸽巢问题》课件(共33张PPT)
文档属性
| 名称 | 人教版六年级数学下册第5单元《鸽巢问题》课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-11 07:44:37 | ||
图片预览








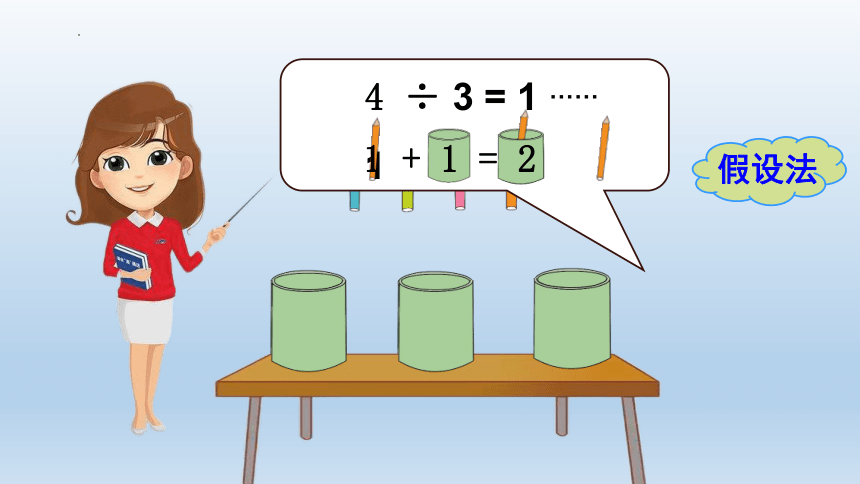
文档简介
(共33张PPT)
鸽巢问题
把4支铅笔放进3个笔筒里,有几种不同的放法呢?不管怎么放,总有笔筒里至少有( )支铅笔。
我在左边笔筒里放 4 支,其他笔筒里一支也没放。
(4 , 0 , 0)
我们小组第一个笔筒里放3支铅笔,第二个笔筒里放1支铅笔,第三个笔筒里不放铅笔,记作(3,1,0)
我们小组第一个笔筒里放2支铅笔,第二个笔筒里放2支铅笔,第三个笔筒里不放铅笔,记作(2,2,0)
我们小组第一个笔筒里放2支铅笔,第二个笔筒里放1支铅笔,第三个笔筒里放1支铅笔,记作(2,1,1)
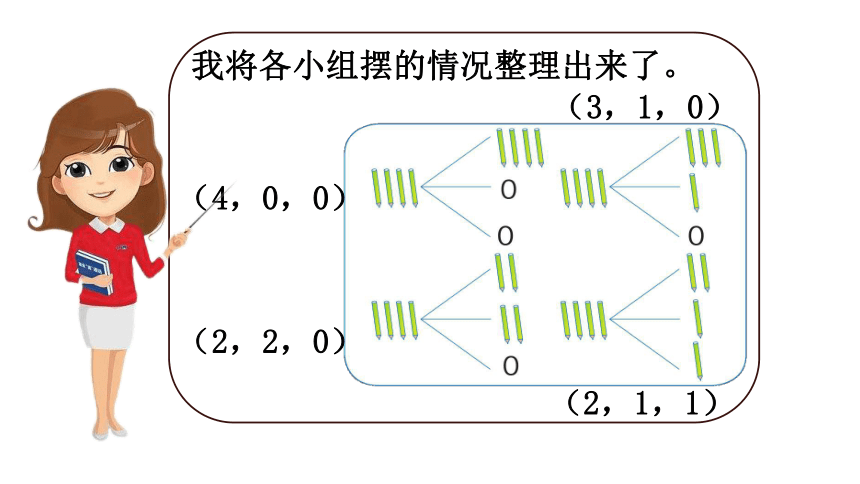
我将各小组摆的情况整理出来了。
(4,0,0)
(3,1,0)
(2,2,0)
(2,1,1)
我将各小组摆的情况整理出来了。
(4,0,0)
(3,1,0)
(2,2,0)
(2,1,1)
枚举法
(4,0,0)
(3,1,0)
(2,2,0)
(2,1,1)
我将各小组摆的情况整理出来了。
“总有”和“至少”是什么意思?
4 ÷ 3 = 1 …… 1
1 + 1 = 2
假设法
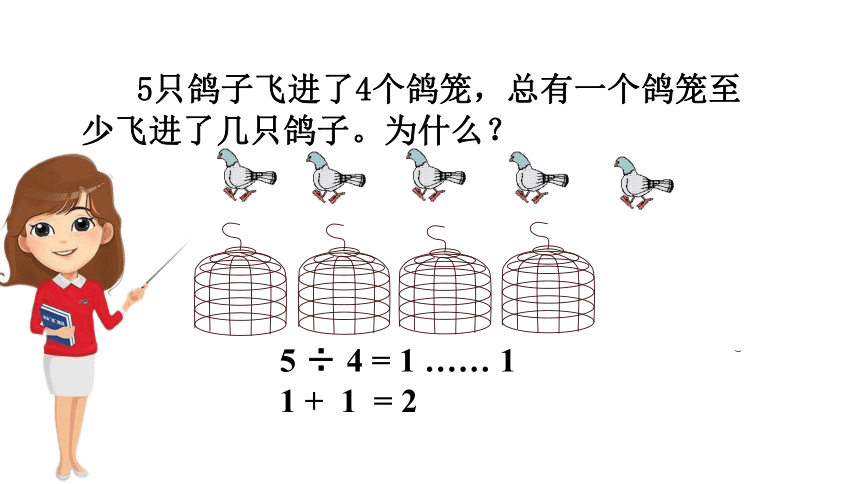
5只鸽子飞进了4个鸽笼,总有一个鸽笼至少飞进了几只鸽子。为什么?
5 ÷ 4 = 1 …… 1
1 + 1 = 2
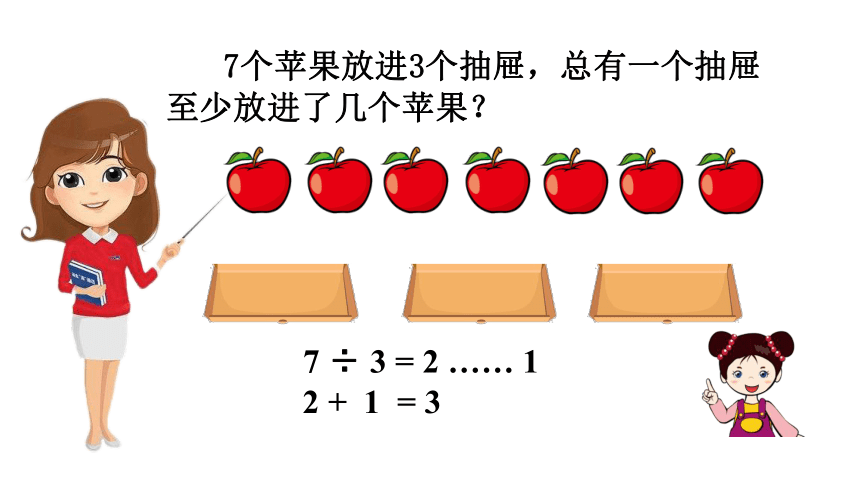
7 ÷ 3 = 2 …… 1
2 + 1 = 3
7个苹果放进3个抽屉,总有一个抽屉至少放进了几个苹果?
8 ÷ 3 = 2 …… 2
2 + 1 = 3
8个苹果放进3个抽屉,总有一个抽屉至少放进了几个苹果?
10 ÷ 3 = 3 …… 1
3 + 1 = 4
10个苹果放进3个盒子,总有一个盒子至少放进了几个苹果?
观察这些算式,你有什么发现?
7÷3=2……1 2+1=3
8÷3=2……2 2+1=3
10÷3=3……1 2+1=3
物体数 抽屉数 = 商……余数
至少数 = 商 + 1
÷
物体数÷抽屉数 = 商……余数
至少数 = 商数 + 1
整除时,至少数 = 商数
鸽巢问题
(抽屉原理)
起源:19世纪的德国数学家狄利克雷
提出,又称“狄利克雷原理”。
作用:广泛应用在解决实际问题。
密室逃脱
答题闯关游戏
为了检查同学们的学习情况,这一次把大家带到了一个封闭的房子里。只有答对所有的题目,才可以走出房子哦。
大家一起加油,逃出密室吧!
开始答题!
5只鸽子飞进了3个鸽笼,总有
1个鸽笼至少飞进了2只鸽子。
为什么?
完成
掉落钥匙一把
进入下一关
进入下一关
张叔叔参加飞镖比赛,投了5镖,成绩是41环。张叔叔至少有一镖不低于( )环?
A:9
B:10
C:8
D:7
掉落钥匙一把
进入下一关
进入下一关
随意找13位老师,他们中至少有2个人的属相相同。
答对了
答错了
掉落钥匙一把
进入下一关
进入下一关
给1个正方体木块的6个面分别涂上蓝、黄两种颜色,不论怎么涂至少有3个面涂的颜色相同。为什么?
掉落钥匙一把
进入下一关
进入下一关
任意给出3个不同的自然数,其中一定有2个数的和是偶数,请说明理由。
掉落钥匙一把
进入下一关
进入下一关
每个小组 6 名同学,总有一
个季节里至少有 2 人过生日。
请说明理由。
完成
掉落钥匙一把
进入下一关
恭喜过关!
恭喜过关!
同学们,今天的数学课你们有哪些收获呢?
再见!!!
鸽巢问题
把4支铅笔放进3个笔筒里,有几种不同的放法呢?不管怎么放,总有笔筒里至少有( )支铅笔。
我在左边笔筒里放 4 支,其他笔筒里一支也没放。
(4 , 0 , 0)
我们小组第一个笔筒里放3支铅笔,第二个笔筒里放1支铅笔,第三个笔筒里不放铅笔,记作(3,1,0)
我们小组第一个笔筒里放2支铅笔,第二个笔筒里放2支铅笔,第三个笔筒里不放铅笔,记作(2,2,0)
我们小组第一个笔筒里放2支铅笔,第二个笔筒里放1支铅笔,第三个笔筒里放1支铅笔,记作(2,1,1)
我将各小组摆的情况整理出来了。
(4,0,0)
(3,1,0)
(2,2,0)
(2,1,1)
我将各小组摆的情况整理出来了。
(4,0,0)
(3,1,0)
(2,2,0)
(2,1,1)
枚举法
(4,0,0)
(3,1,0)
(2,2,0)
(2,1,1)
我将各小组摆的情况整理出来了。
“总有”和“至少”是什么意思?
4 ÷ 3 = 1 …… 1
1 + 1 = 2
假设法
5只鸽子飞进了4个鸽笼,总有一个鸽笼至少飞进了几只鸽子。为什么?
5 ÷ 4 = 1 …… 1
1 + 1 = 2
7 ÷ 3 = 2 …… 1
2 + 1 = 3
7个苹果放进3个抽屉,总有一个抽屉至少放进了几个苹果?
8 ÷ 3 = 2 …… 2
2 + 1 = 3
8个苹果放进3个抽屉,总有一个抽屉至少放进了几个苹果?
10 ÷ 3 = 3 …… 1
3 + 1 = 4
10个苹果放进3个盒子,总有一个盒子至少放进了几个苹果?
观察这些算式,你有什么发现?
7÷3=2……1 2+1=3
8÷3=2……2 2+1=3
10÷3=3……1 2+1=3
物体数 抽屉数 = 商……余数
至少数 = 商 + 1
÷
物体数÷抽屉数 = 商……余数
至少数 = 商数 + 1
整除时,至少数 = 商数
鸽巢问题
(抽屉原理)
起源:19世纪的德国数学家狄利克雷
提出,又称“狄利克雷原理”。
作用:广泛应用在解决实际问题。
密室逃脱
答题闯关游戏
为了检查同学们的学习情况,这一次把大家带到了一个封闭的房子里。只有答对所有的题目,才可以走出房子哦。
大家一起加油,逃出密室吧!
开始答题!
5只鸽子飞进了3个鸽笼,总有
1个鸽笼至少飞进了2只鸽子。
为什么?
完成
掉落钥匙一把
进入下一关
进入下一关
张叔叔参加飞镖比赛,投了5镖,成绩是41环。张叔叔至少有一镖不低于( )环?
A:9
B:10
C:8
D:7
掉落钥匙一把
进入下一关
进入下一关
随意找13位老师,他们中至少有2个人的属相相同。
答对了
答错了
掉落钥匙一把
进入下一关
进入下一关
给1个正方体木块的6个面分别涂上蓝、黄两种颜色,不论怎么涂至少有3个面涂的颜色相同。为什么?
掉落钥匙一把
进入下一关
进入下一关
任意给出3个不同的自然数,其中一定有2个数的和是偶数,请说明理由。
掉落钥匙一把
进入下一关
进入下一关
每个小组 6 名同学,总有一
个季节里至少有 2 人过生日。
请说明理由。
完成
掉落钥匙一把
进入下一关
恭喜过关!
恭喜过关!
同学们,今天的数学课你们有哪些收获呢?
再见!!!
