2015九年级数学北师大新版教学同步课件:1-6利用三角函数测高
文档属性
| 名称 | 2015九年级数学北师大新版教学同步课件:1-6利用三角函数测高 |

|
|
| 格式 | zip | ||
| 文件大小 | 715.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-25 00:00:00 | ||
图片预览




文档简介
课件15张PPT。北师大版九年级下册第一章1.6利用三角函数测高一、如何测量倾斜角
测量倾斜角可以用测倾器。
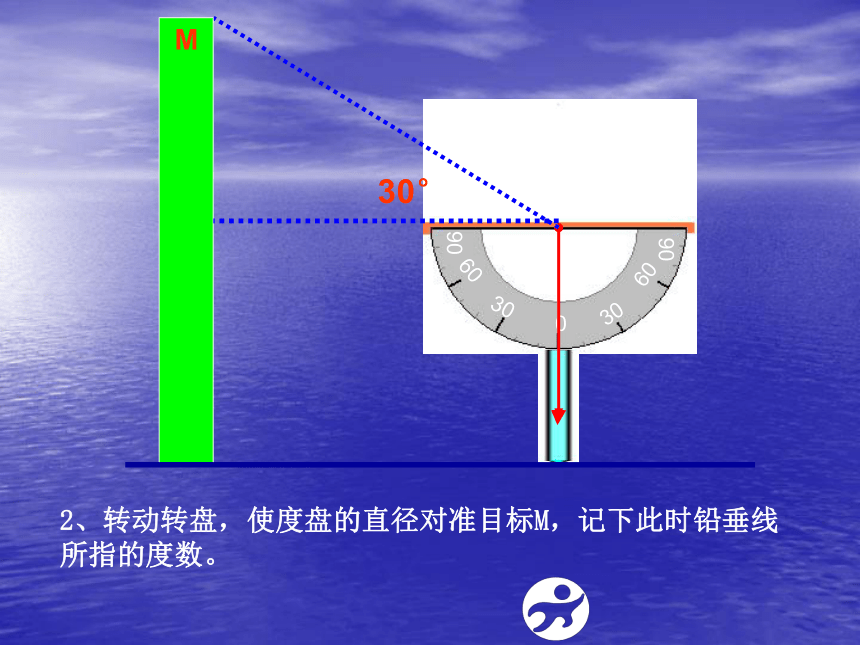
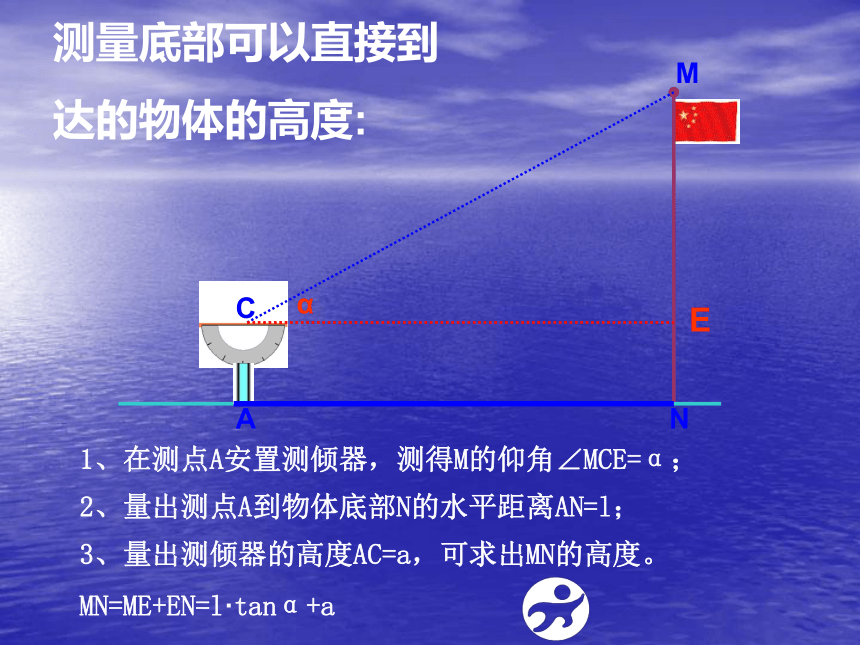
----简单的侧倾器由度盘、铅锤和支杆组成使用测倾器测量倾斜角的步骤如下:1、把支架竖直插入地面,使支架的中心线、铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置。PQ2、转动转盘,使度盘的直径对准目标M,记下此时铅垂线所指的度数。30°ACMN1、在测点A安置测倾器,测得M的仰角∠MCE=α;E2、量出测点A到物体底部N的水平距离AN=l;3、量出测倾器的高度AC=a,可求出MN的高度。
MN=ME+EN=l·tanα+a测量底部可以直接到
达的物体的高度:α如图,某中学在主楼的顶部和大门的上方之间挂一些彩旗.经测量,得到大门的高度是5m,大门距主楼的距离是30m,在大门处测得主楼顶部的仰角是30°,而当时侧倾器离地面1.4m,求学校主楼的高度 (精确到0.01m) 解:如图,作EM垂直CD于M点,根据题意,可知
EB=1.4m,∠DEM=30°,BC=EM=30 m, CM=BE=1.4m
在Rt△DEM中,DM=EMtan30°≈30×0.577 =17.32(m)
CD=DM+CM=17.32+1.4=18.72(m)
生活应用1测量底部不可以直接到
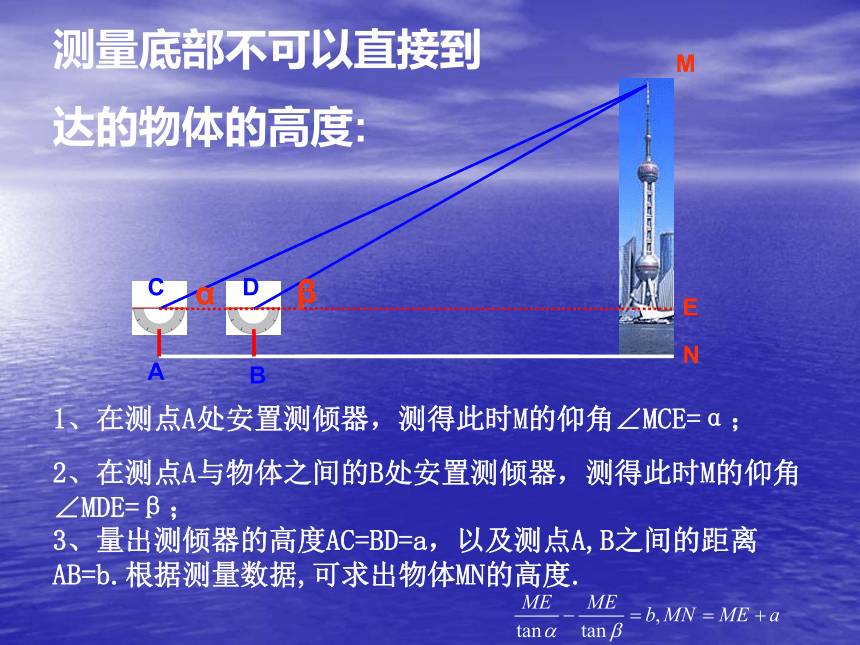
达的物体的高度:1、在测点A处安置测倾器,测得此时M的仰角∠MCE=α;ACBDMNEα2、在测点A与物体之间的B处安置测倾器,测得此时M的仰角∠MDE=β;β3、量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.根据测量数据,可求出物体MN的高度.生活应用21.请根据小亮测得的数据,填写表中的空格; 2.通过计算得,地王大厦的高为(已知测倾器的高CE=DF=1m)______m (精确到1m).2. 在Rt△AEG中,EG=AG/tan30°=1.732AG
在Rt△AFG中,FG=AG/tan45°=AG
EG-FG=CD
1.732AG-AG=60
AG=60÷0.732≈81.96
AB=AG+1≈83(m)
1. 30°, 45°, 60m课内拓展应用1.大楼AD的高为100米,远处有一塔BC,某人在楼底A处测得塔顶B处的仰角为60°,爬到楼顶D测得塔顶B点仰角为30°,求塔BC的高度.2.如图,在离铁塔150米的A处,用测角仪测得塔顶的仰角为30°,已知测角仪高AD=1.5米,求铁塔高BE.AD(1)侧倾器的使用
(2)误差的解决办法---用平均值 总 结(3)到目前为止,你有那些测量物体高度的方法? 测量底部可以到达的
物体的高度,如左图测量底部不可以直接到达
的物体的高度,如右图
作 业 1. 分组制作简单的测倾器.2.选择一个底部可以到达的物体,测量它的高度并撰写一份活动报告,阐明活动课题、测量示意图、测得数据和计算过程等.3.选择一个底部不可以到达的物体,测量它的高度并撰写一份活动报告,阐明活动课题、测量示意图、测得数据和计算过程等.
(下表作参考)
活动报告
测量倾斜角可以用测倾器。
----简单的侧倾器由度盘、铅锤和支杆组成使用测倾器测量倾斜角的步骤如下:1、把支架竖直插入地面,使支架的中心线、铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置。PQ2、转动转盘,使度盘的直径对准目标M,记下此时铅垂线所指的度数。30°ACMN1、在测点A安置测倾器,测得M的仰角∠MCE=α;E2、量出测点A到物体底部N的水平距离AN=l;3、量出测倾器的高度AC=a,可求出MN的高度。
MN=ME+EN=l·tanα+a测量底部可以直接到
达的物体的高度:α如图,某中学在主楼的顶部和大门的上方之间挂一些彩旗.经测量,得到大门的高度是5m,大门距主楼的距离是30m,在大门处测得主楼顶部的仰角是30°,而当时侧倾器离地面1.4m,求学校主楼的高度 (精确到0.01m) 解:如图,作EM垂直CD于M点,根据题意,可知
EB=1.4m,∠DEM=30°,BC=EM=30 m, CM=BE=1.4m
在Rt△DEM中,DM=EMtan30°≈30×0.577 =17.32(m)
CD=DM+CM=17.32+1.4=18.72(m)
生活应用1测量底部不可以直接到
达的物体的高度:1、在测点A处安置测倾器,测得此时M的仰角∠MCE=α;ACBDMNEα2、在测点A与物体之间的B处安置测倾器,测得此时M的仰角∠MDE=β;β3、量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.根据测量数据,可求出物体MN的高度.生活应用21.请根据小亮测得的数据,填写表中的空格; 2.通过计算得,地王大厦的高为(已知测倾器的高CE=DF=1m)______m (精确到1m).2. 在Rt△AEG中,EG=AG/tan30°=1.732AG
在Rt△AFG中,FG=AG/tan45°=AG
EG-FG=CD
1.732AG-AG=60
AG=60÷0.732≈81.96
AB=AG+1≈83(m)
1. 30°, 45°, 60m课内拓展应用1.大楼AD的高为100米,远处有一塔BC,某人在楼底A处测得塔顶B处的仰角为60°,爬到楼顶D测得塔顶B点仰角为30°,求塔BC的高度.2.如图,在离铁塔150米的A处,用测角仪测得塔顶的仰角为30°,已知测角仪高AD=1.5米,求铁塔高BE.AD(1)侧倾器的使用
(2)误差的解决办法---用平均值 总 结(3)到目前为止,你有那些测量物体高度的方法? 测量底部可以到达的
物体的高度,如左图测量底部不可以直接到达
的物体的高度,如右图
作 业 1. 分组制作简单的测倾器.2.选择一个底部可以到达的物体,测量它的高度并撰写一份活动报告,阐明活动课题、测量示意图、测得数据和计算过程等.3.选择一个底部不可以到达的物体,测量它的高度并撰写一份活动报告,阐明活动课题、测量示意图、测得数据和计算过程等.
(下表作参考)
活动报告
