第二十三章 旋转 单元检测试题 2023--2024学年人教版九年级数学上册(含答案解析)
文档属性
| 名称 | 第二十三章 旋转 单元检测试题 2023--2024学年人教版九年级数学上册(含答案解析) | 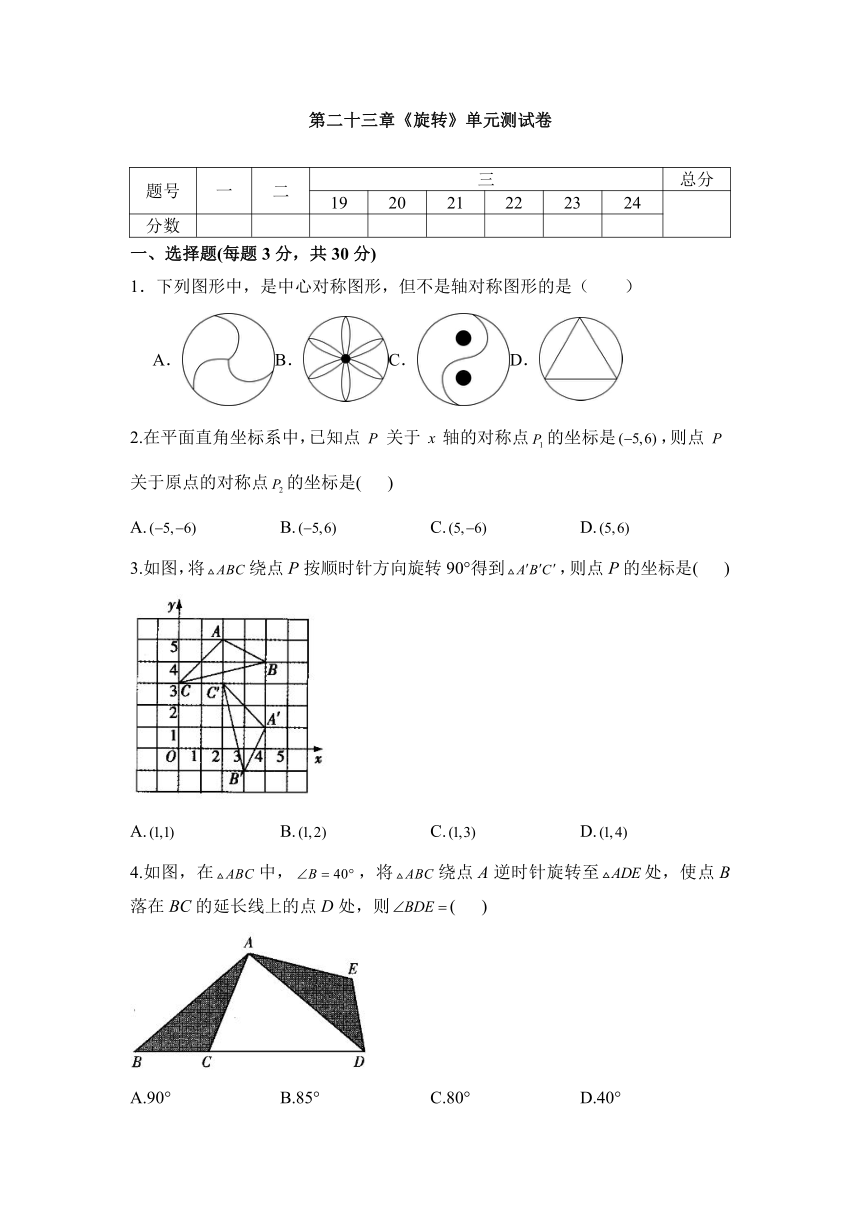 | |
| 格式 | docx | ||
| 文件大小 | 497.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-12 18:38:06 | ||
图片预览




文档简介
第二十三章《旋转》单元测试卷
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分,共30分)
1.下列图形中,是中心对称图形,但不是轴对称图形的是( )
A.B.C.D.
2.在平面直角坐标系中,已知点关于轴的对称点的坐标是,则点关于原点的对称点的坐标是( )
A. B. C. D.
3.如图,将绕点P按顺时针方向旋转90°得到,则点P的坐标是( )
A. B. C. D.
4.如图,在中,,将绕点A逆时针旋转至处,使点B落在BC的延长线上的点D处,则( )
A.90° B.85° C.80° D.40°
5.如图,将绕点逆时针旋转得到,点的对应点恰好在边上,交于点,若,则的度数为( )
A. B. C. D.
6.如图,将边长为的正方形绕点B逆时针旋转30°,那么图中点M的坐标为( )
A.(,1) B.(1,) C.(,) D.(,)
7.两块大小相同,含有30°角的直角三角板如图水平放置,将△CDE绕点C按逆时针方向旋转,当点E的对应点E′恰好落在AB上时,△CDE旋转的角度是( )
A.30° B.35° C.40° D.60°
8.如图,点B在第一象限,点A在x轴的正半轴上∠AOB=∠B=30°,OA=2,将△AOB绕点O逆时针旋转90°,则点B的对应点B′的坐标是()
A.(﹣,3) B.(﹣3,) C.(﹣,) D.(﹣2,3)
9.将按如图方式放在平面直角坐标系中,其中,,顶点的坐标为,将绕原点逆时针旋转,每次旋转60°,则第2023次旋转结束时,点对应点的坐标为( )
A. B.C.D.
10.如图所示的各图中可看成由下方图形绕着一个顶点顺时针旋转90°而形成的图形的是( )
A.B.C.D.
二、填空题(每题3分,共24分)
11.如图,将绕点A逆时针旋转一定角度,得到.若,,则的度数为__________度.
12.若点在轴上,则点关于原点对称的点的坐标为_______.
13.如图,设P为等边三角形ABC内的一点,且,,,则___________.
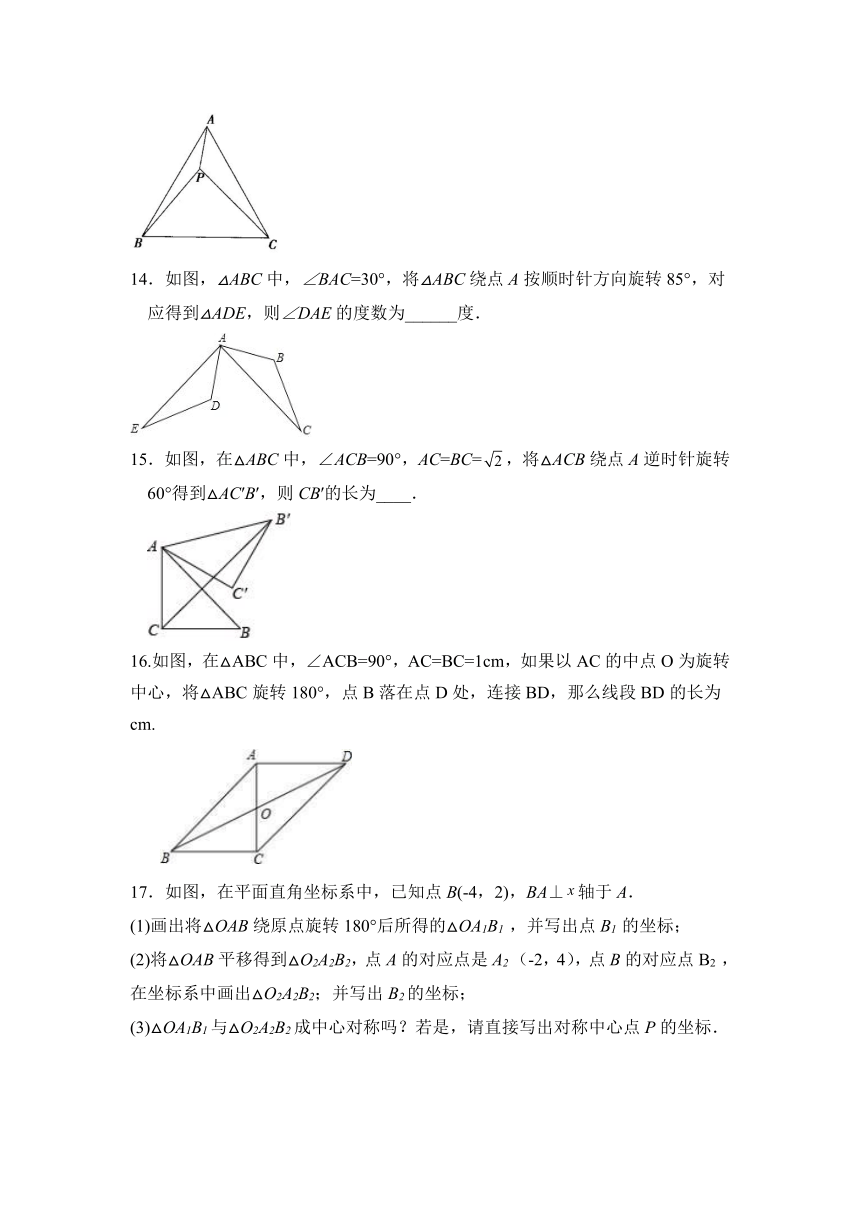
14.如图,△ABC中,∠BAC=30°,将△ABC绕点A按顺时针方向旋转85°,对应得到△ADE,则∠DAE的度数为______度.
15.如图,在△ABC中,∠ACB=90°,AC=BC=,将△ACB绕点A逆时针旋转60°得到△AC′B′,则CB′的长为____.
16.如图,在△ABC中,∠ACB=90°,AC=BC=1cm,如果以AC的中点O为旋转
中心,将△ABC旋转180°,点B落在点D处,连接BD,那么线段BD的长为
cm.
17.如图,在平面直角坐标系中,已知点B(-4,2),BA⊥轴于A.
(1)画出将△OAB绕原点旋转180°后所得的△OA1B1 ,并写出点B1 的坐标;
(2)将△OAB平移得到△O2A2B2,点A的对应点是A2 (-2,4),点B的对应点B2 ,在坐标系中画出△O2A2B2;并写出B2的坐标;
(3)△OA1B1与△O2A2B2成中心对称吗?若是,请直接写出对称中心点P的坐标.
18.如图,已知矩形OABC的边OA、OC分别在x在轴、y轴上,点B的坐标为(4,4),将△AOC绕着点A逆时针旋转,使点C的对应点C1落在y轴上,点O的对应点为O1,连接O1C若点P为O1C的中点,则点P到x轴的距离为.
三.解答题(共46分,19题6分,20 ---24题8分)
19.如图,在的方格纸中,△ABC的顶点均在格点上,请按下列要求完成作图.
(1)在图1中,将△ABC绕C点顺时针方向旋转90°,得到△A1B1C.
(2)在图2中,在AC所在直线的左侧画∠AEC,使得∠AEC=∠B.
20.如图,△ABC中,AB=AC=2,∠BAC=45°,△AEF是由△ABC绕点A按逆时针方向旋转得到的,连接BE、CF相交于点D,求证:BE=CF.
21.如图,四边形ABCD是正方形,△ADF绕着点A顺时旋转90°得到△ABE,若AF=4,AB=7.
(1)求DE的长度;
(2)指出BE与DF的关系如何?并说明由.
22.如图,已知:如图点,点在轴正半轴上,且,将线段绕点沿顺时针旋转,设点旋转后的对应点是点,求点的坐标.
23.如图1:在等边△ABC中,点D,E分别在边AB,AC上,AD=AE,连结BE,CD,点M、N、P分别是BE、CD、BC的中点.
(1)观察猜想
图1中△PMN的形状是;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,△PMN的形状是否发生改变?并说明理由.
24. 如图,四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,AB=7,求:
(1)指出旋转中心和旋转角度;
(2)求DE的长度;
(3)BE与DF的位置关系如何?
参考答案
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C D B C B D A A B B
二、填空题(每题3分,共24分)
11.答案:85
12.答案:
13.答案:150°
14.30.
15.
16.答案为:.
17. 90.
18. 90;240.
三.解答题(共46分,19题6分,20 ---24题8分)
19.(1)解:如图1,△A1B1C即为所求;
(2)解:如图2,点E或E′即为所求;
20.证明:如图,∵△AEF是由△ABC绕点A按逆时针方向旋转得到的,∴AE=AF=AB=AC=2,∠EAF=∠BAC=45°,∴∠BAC+∠3=∠EAF+∠3,即∠BAE=∠CAF,在△ABE和△ACF中,,∴△ABE≌△ACF,∴BE=CF.
21.(1)3;(2)BE=DF,BE⊥DF.
【详解】
解:(1)∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴AE=AF=4,AD=AB=7,
∴DE=AD﹣AE=7﹣4=3;
(2)BE、DF的关系为:BE=DF,BE⊥DF.理由如下:
∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴△ABE≌△ADF,
∴BE=DF,∠ABE=∠ADF,
∵∠ADF+∠F=180°﹣90°=90°,
∴∠ABE+∠F=90°,
∴BE⊥DF,
∴BE、DF的关系为:BE=DF,BE⊥DF.
22.点的坐标为.
【详解】
解:如图,作轴于,
∵,,
∴,
∵线段绕点沿逆时针旋转得,
∴,且,
∴
而,
∴,
在和中
,
∴,
∴,,
∴,
∴点的坐标为.
23. (1)等边三角形;(2)△PMN的形状不发生改变,仍为等边三角形
24. 【答案】(1)解:根据正方形的性质可知:△AFD≌△AEB,
即AE=AF=4,∠EAF=90°,∠EBA=∠FDA;
可得旋转中心为点A;
旋转角度为:90°或270°;
(2)解:DE=AD AE=7 4=3
(3)解:BE⊥DF ;
延长BE交DF于点G
由旋转△ADF≌△ABE
∴∠ADF=∠ABE
又∵∠DEG=∠AEB
∴∠DGE=∠EAB=90°
∴BE⊥DF
【解析】【分析】(1)利用已知条件:△ADF旋转一定角度后得到△ABE,结合正方形的性质,可证得AE=AF=4,∠EAF=90°,∠EBA=∠FDA;即可得到旋转中心及旋转角度.
(2)利用DE=AD-AE,代入计算求出DE的长.
(3)延长BE交DF于点G,利用旋转的性质可证得△ADF≌△ABE;再利用全等三角形的性质可证得∠ADF=∠ABE;然后证明∠DGE=∠EAB=90°,利用垂直的定义可证得结论.
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分,共30分)
1.下列图形中,是中心对称图形,但不是轴对称图形的是( )
A.B.C.D.
2.在平面直角坐标系中,已知点关于轴的对称点的坐标是,则点关于原点的对称点的坐标是( )
A. B. C. D.
3.如图,将绕点P按顺时针方向旋转90°得到,则点P的坐标是( )
A. B. C. D.
4.如图,在中,,将绕点A逆时针旋转至处,使点B落在BC的延长线上的点D处,则( )
A.90° B.85° C.80° D.40°
5.如图,将绕点逆时针旋转得到,点的对应点恰好在边上,交于点,若,则的度数为( )
A. B. C. D.
6.如图,将边长为的正方形绕点B逆时针旋转30°,那么图中点M的坐标为( )
A.(,1) B.(1,) C.(,) D.(,)
7.两块大小相同,含有30°角的直角三角板如图水平放置,将△CDE绕点C按逆时针方向旋转,当点E的对应点E′恰好落在AB上时,△CDE旋转的角度是( )
A.30° B.35° C.40° D.60°
8.如图,点B在第一象限,点A在x轴的正半轴上∠AOB=∠B=30°,OA=2,将△AOB绕点O逆时针旋转90°,则点B的对应点B′的坐标是()
A.(﹣,3) B.(﹣3,) C.(﹣,) D.(﹣2,3)
9.将按如图方式放在平面直角坐标系中,其中,,顶点的坐标为,将绕原点逆时针旋转,每次旋转60°,则第2023次旋转结束时,点对应点的坐标为( )
A. B.C.D.
10.如图所示的各图中可看成由下方图形绕着一个顶点顺时针旋转90°而形成的图形的是( )
A.B.C.D.
二、填空题(每题3分,共24分)
11.如图,将绕点A逆时针旋转一定角度,得到.若,,则的度数为__________度.
12.若点在轴上,则点关于原点对称的点的坐标为_______.
13.如图,设P为等边三角形ABC内的一点,且,,,则___________.
14.如图,△ABC中,∠BAC=30°,将△ABC绕点A按顺时针方向旋转85°,对应得到△ADE,则∠DAE的度数为______度.
15.如图,在△ABC中,∠ACB=90°,AC=BC=,将△ACB绕点A逆时针旋转60°得到△AC′B′,则CB′的长为____.
16.如图,在△ABC中,∠ACB=90°,AC=BC=1cm,如果以AC的中点O为旋转
中心,将△ABC旋转180°,点B落在点D处,连接BD,那么线段BD的长为
cm.
17.如图,在平面直角坐标系中,已知点B(-4,2),BA⊥轴于A.
(1)画出将△OAB绕原点旋转180°后所得的△OA1B1 ,并写出点B1 的坐标;
(2)将△OAB平移得到△O2A2B2,点A的对应点是A2 (-2,4),点B的对应点B2 ,在坐标系中画出△O2A2B2;并写出B2的坐标;
(3)△OA1B1与△O2A2B2成中心对称吗?若是,请直接写出对称中心点P的坐标.
18.如图,已知矩形OABC的边OA、OC分别在x在轴、y轴上,点B的坐标为(4,4),将△AOC绕着点A逆时针旋转,使点C的对应点C1落在y轴上,点O的对应点为O1,连接O1C若点P为O1C的中点,则点P到x轴的距离为.
三.解答题(共46分,19题6分,20 ---24题8分)
19.如图,在的方格纸中,△ABC的顶点均在格点上,请按下列要求完成作图.
(1)在图1中,将△ABC绕C点顺时针方向旋转90°,得到△A1B1C.
(2)在图2中,在AC所在直线的左侧画∠AEC,使得∠AEC=∠B.
20.如图,△ABC中,AB=AC=2,∠BAC=45°,△AEF是由△ABC绕点A按逆时针方向旋转得到的,连接BE、CF相交于点D,求证:BE=CF.
21.如图,四边形ABCD是正方形,△ADF绕着点A顺时旋转90°得到△ABE,若AF=4,AB=7.
(1)求DE的长度;
(2)指出BE与DF的关系如何?并说明由.
22.如图,已知:如图点,点在轴正半轴上,且,将线段绕点沿顺时针旋转,设点旋转后的对应点是点,求点的坐标.
23.如图1:在等边△ABC中,点D,E分别在边AB,AC上,AD=AE,连结BE,CD,点M、N、P分别是BE、CD、BC的中点.
(1)观察猜想
图1中△PMN的形状是;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,△PMN的形状是否发生改变?并说明理由.
24. 如图,四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,AB=7,求:
(1)指出旋转中心和旋转角度;
(2)求DE的长度;
(3)BE与DF的位置关系如何?
参考答案
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C D B C B D A A B B
二、填空题(每题3分,共24分)
11.答案:85
12.答案:
13.答案:150°
14.30.
15.
16.答案为:.
17. 90.
18. 90;240.
三.解答题(共46分,19题6分,20 ---24题8分)
19.(1)解:如图1,△A1B1C即为所求;
(2)解:如图2,点E或E′即为所求;
20.证明:如图,∵△AEF是由△ABC绕点A按逆时针方向旋转得到的,∴AE=AF=AB=AC=2,∠EAF=∠BAC=45°,∴∠BAC+∠3=∠EAF+∠3,即∠BAE=∠CAF,在△ABE和△ACF中,,∴△ABE≌△ACF,∴BE=CF.
21.(1)3;(2)BE=DF,BE⊥DF.
【详解】
解:(1)∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴AE=AF=4,AD=AB=7,
∴DE=AD﹣AE=7﹣4=3;
(2)BE、DF的关系为:BE=DF,BE⊥DF.理由如下:
∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴△ABE≌△ADF,
∴BE=DF,∠ABE=∠ADF,
∵∠ADF+∠F=180°﹣90°=90°,
∴∠ABE+∠F=90°,
∴BE⊥DF,
∴BE、DF的关系为:BE=DF,BE⊥DF.
22.点的坐标为.
【详解】
解:如图,作轴于,
∵,,
∴,
∵线段绕点沿逆时针旋转得,
∴,且,
∴
而,
∴,
在和中
,
∴,
∴,,
∴,
∴点的坐标为.
23. (1)等边三角形;(2)△PMN的形状不发生改变,仍为等边三角形
24. 【答案】(1)解:根据正方形的性质可知:△AFD≌△AEB,
即AE=AF=4,∠EAF=90°,∠EBA=∠FDA;
可得旋转中心为点A;
旋转角度为:90°或270°;
(2)解:DE=AD AE=7 4=3
(3)解:BE⊥DF ;
延长BE交DF于点G
由旋转△ADF≌△ABE
∴∠ADF=∠ABE
又∵∠DEG=∠AEB
∴∠DGE=∠EAB=90°
∴BE⊥DF
【解析】【分析】(1)利用已知条件:△ADF旋转一定角度后得到△ABE,结合正方形的性质,可证得AE=AF=4,∠EAF=90°,∠EBA=∠FDA;即可得到旋转中心及旋转角度.
(2)利用DE=AD-AE,代入计算求出DE的长.
(3)延长BE交DF于点G,利用旋转的性质可证得△ADF≌△ABE;再利用全等三角形的性质可证得∠ADF=∠ABE;然后证明∠DGE=∠EAB=90°,利用垂直的定义可证得结论.
同课章节目录
