第六章 反比例函数 单元测试题(无答案) 2023—2024学年北师大版九年级数学上册
文档属性
| 名称 | 第六章 反比例函数 单元测试题(无答案) 2023—2024学年北师大版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 328.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-11 21:31:34 | ||
图片预览

文档简介
第六章 反比例函数 单元测试题 2023-2024学年北师大版九年级数学上册
(考试时间120分钟,满分150分)
一、选择题(本大题共10小题,每小题4分,共40分)
1.下列函数中,y是x的反比例函数的是( )
A. B. C.y=-3x D.
2.下列选项中,反比例函数的图象一定经过的点是( )
A.(1,4) B.(-1,-4) C.(-2,2) D.(2,2)
3.若反比例函数在每一个象限内y的值都随x值的增大而增大,则k的值可能是
( )
A.-3 B.-1 C.0 D.
4.若A(x1,-6),B(x2,-2),C(x3,3)都在反比例函数的图象上,则x1,x2,x3的大小关系为
( )
A.x35.如图,直线y=kx(k>0)与双曲线交于A,B两点,若A(2,m),则点B的坐标为( )
A.(2,2) B.(-2,-1) C.(-2,-2) D.(-1,-4)
6.近视眼镜的度数y(度)与镜片焦距x(米)之间具有如图所示的反比例函数关系.小明原来佩戴400度的近视眼镜,经过一段时间的矫正治疗,复查验光时,所配镜片焦距调整为0.4米,则小明的眼镜度数( )
A.下降了150度 B.下降了250度 C.下降了350度 D.不变
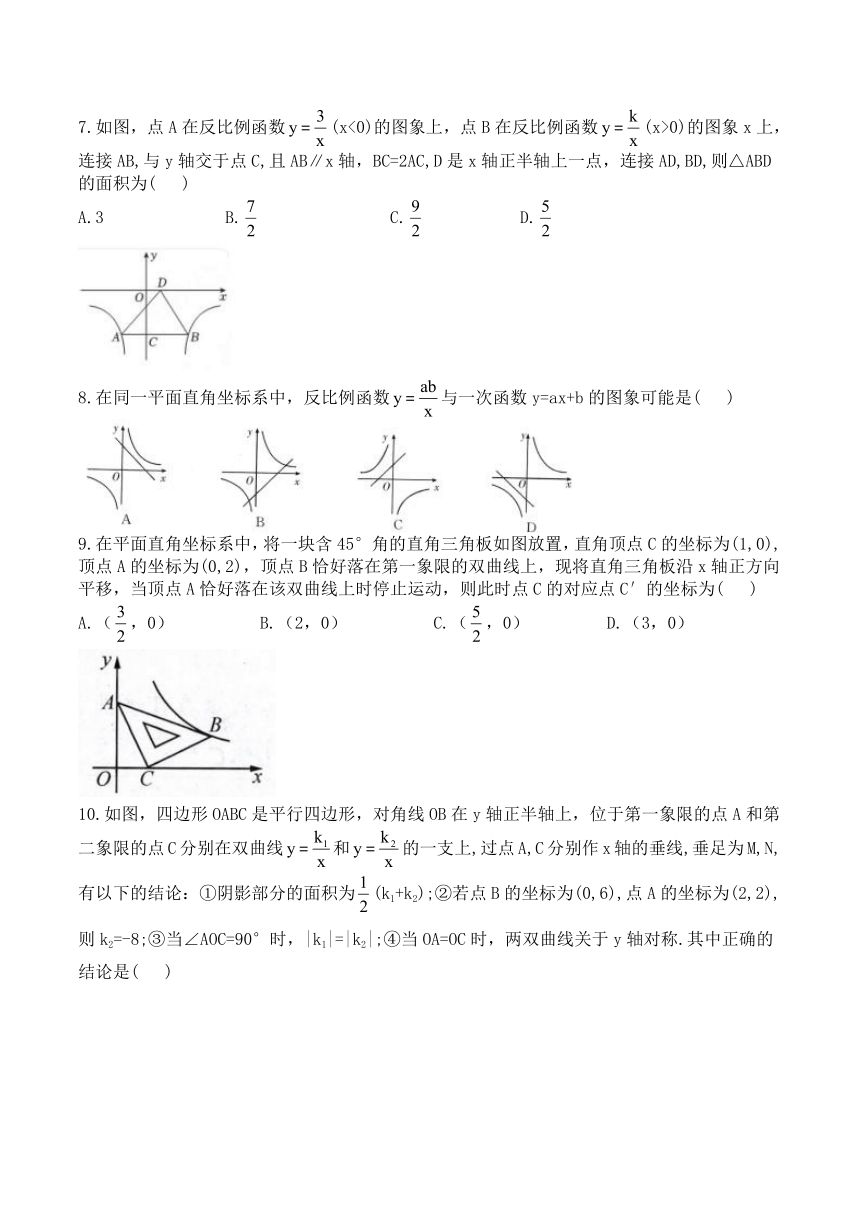
7.如图,点A在反比例函数(x<0)的图象上,点B在反比例函数(x>0)的图象x上,连接AB,与y轴交于点C,且AB∥x轴,BC=2AC,D是x轴正半轴上一点,连接AD,BD,则△ABD的面积为( )
A.3 B. C. D.
8.在同一平面直角坐标系中,反比例函数与一次函数y=ax+b的图象可能是( )
9.在平面直角坐标系中,将一块含45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )
A.(,0) B.(2,0) C.(,0) D.(3,0)
10.如图,四边形OABC是平行四边形,对角线OB在y轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线和的一支上,过点A,C分别作x轴的垂线,垂足为M,N,有以下的结论:①阴影部分的面积为(k1+k2);②若点B的坐标为(0,6),点A的坐标为(2,2),则k2=-8;③当∠AOC=90°时,|k1|=|k2|;④当OA=OC时,两双曲线关于y轴对称.其中正确的结论是( )
A.①②③④⑤ B.②③④ C.①②③ D.②④
二、填空题(本大题共5小题,每小题4分,共20分)
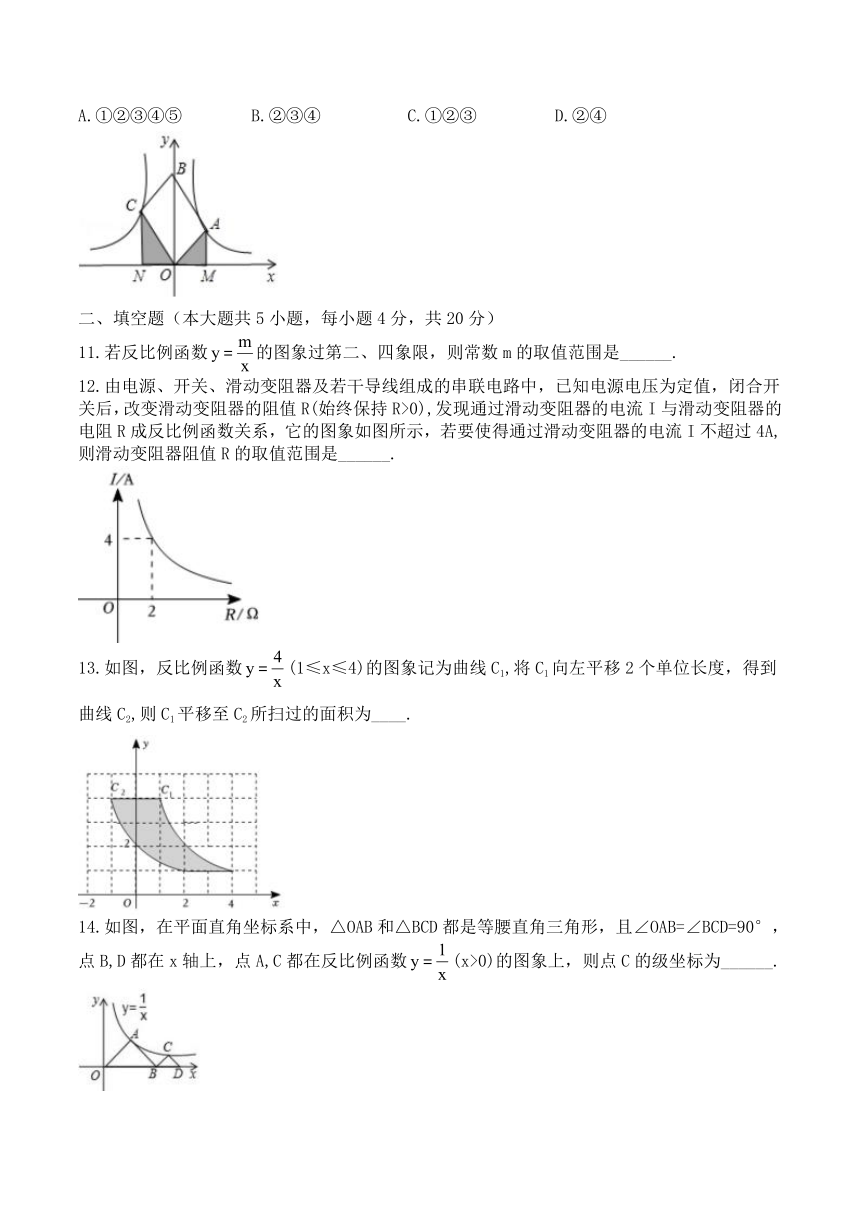
11.若反比例函数的图象过第二、四象限,则常数m的取值范围是______.
12.由电源、开关、滑动变阻器及若干导线组成的串联电路中,已知电源电压为定值,闭合开关后,改变滑动变阻器的阻值R(始终保持R>0),发现通过滑动变阻器的电流I与滑动变阻器的电阻R成反比例函数关系,它的图象如图所示,若要使得通过滑动变阻器的电流I不超过4A,则滑动变阻器阻值R的取值范围是______.
13.如图,反比例函数(1≤x≤4)的图象记为曲线C1,将C1向左平移2个单位长度,得到曲线C2,则C1平移至C2所扫过的面积为____.
14.如图,在平面直角坐标系中,△OAB和△BCD都是等腰直角三角形,且∠OAB=∠BCD=90°,点B,D都在x轴上,点A,C都在反比例函数(x>0)的图象上,则点C的级坐标为______.
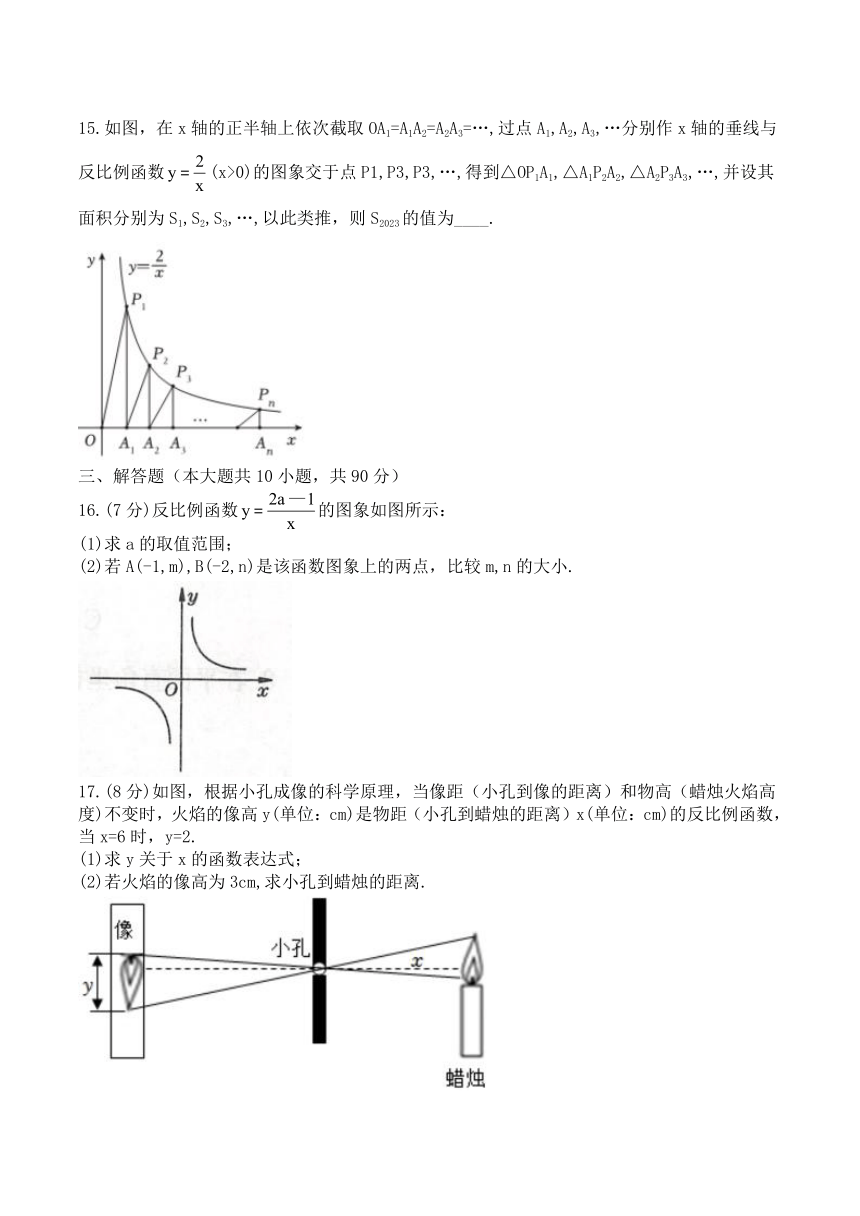
15.如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3=…,过点A1,A2,A3,…分别作x轴的垂线与反比例函数(x>0)的图象交于点P1,P3,P3,…,得到△OP1A1,△A1P2A2,△A2P3A3,…,并设其面积分别为S1,S2,S3,…,以此类推,则S2023的值为____.
三、解答题(本大题共10小题,共90分)
16.(7分)反比例函数的图象如图所示:
(1)求a的取值范围;
(2)若A(-1,m),B(-2,n)是该函数图象上的两点,比较m,n的大小.
17.(8分)如图,根据小孔成像的科学原理,当像距(小孔到像的距离)和物高(蜡烛火焰高度)不变时,火焰的像高y(单位:cm)是物距(小孔到蜡烛的距离)x(单位:cm)的反比例函数,当x=6时,y=2.
(1)求y关于x的函数表达式;
(2)若火焰的像高为3cm,求小孔到蜡烛的距离.
18.(8分)已知y=y1+y2,y1与x成正比例,y2与x成反比例,且当x=-1时,y=5;当x=2时,y=-4.求y与x之间的函数关系式.
19.(8分)如图,在平面直角坐标系中,反比例函数(k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,若△AOB的面积为5.
(1)求k和m的值;
(2)当x≥8时,求函数值y的取值范围.
20.(8分)如图,在平面直角坐标系中,点A的坐标为(-6,4),反比例函数(k≠0)的图象经过OA的中点B,AD⊥y轴于点D,且交反比例函数图象于点C,连接BC,求四边形OBCD的面积.
21.(9分)如图①,将一长方体A放置于一水平玻璃桌面上,按不同的方式摆放,记录桌面所受压强p(Pa)与受力面积S(m2)的关系如下表所示:
(1)求桌面所受压强p(Pa)与受力面积S(m2)之间的函数表达式;
(2)现将另一长、宽、高分别为0.2m,0.3m,0.2m的长方体B按图②所示的方式放置于该水平玻璃桌面上,若桌面所受压强p(Pa)与受力面积S(m2)之间的关系满足(1)中的函数表达式,且该玻璃桌面能承受的最大压强为5000 Pa,请你判断这种摆放方式是否安全?并说明理由.
22.(9分)如图,在平面直角坐标系中,△OAC的边OC在y轴上,反比例函数(x>0)的图象经过点A和点B(2,6),且B为AC的中点.
(1)求k的值和点C的坐标;
(2)求△OAC的周长.
23.(10分)在平面直角坐标系中,一次函数y=2x+b的图象与x轴的交点为A(2,0),与y轴的交点为B,直线AB与反比例函数的图象交于点C(-1,m).
(1)求一次函数和反比例函数的表达式;
(2)求关于x的不等式2x+b>的解集;
(3)P是反比例函数图象上的点,过点P作PM⊥x轴,垂足为M,连接OP,BM,当S△ABM=2S△OMP时,求点P的坐标.
(11分)某数学活动小组在研究反比例函数图象与几何图形的位置关系时,经历了如下过程:如图①,正方形ABCD在平面直角坐标系的第一象限,AB∥x轴,AD∥y轴,A(m,n),AB=a
(1)数学思考:若存在一个反比例函数(k≠0)的图象同时经过点B,D,则m与n之间的x
数量关系为______.
(2)数学应用:①若A(1,1),AB=2,反比例函数(k1≠0)的图象同时经过点B,D,则k1=______.
②在①的条件下,如图②,点E,F分别在BC,DC的延长线上,且CE=CF=1,若反比例函数(k2≠0)的图象同时经过点E,F,则k2=_______.
③在②的条件下,若点P,Q在反比例函数(k3≠0)的图象上,且四边形EFPQ是正方形,求k3的值.
25.(12分)如图①,在平面直角坐标系中,矩形OABC的边OC,OA分别在坐标轴上,且OA=3,0C=6,反比例函数(x>0)的图象与AB,BC分别交于点D,E,连接DE.
(1)如图②,连接OD,OE,当△OAD的面积为2时,
①k=______.
②求△ODE的面积;
(2)如图③,将△DEB沿DE翻折,当点B的对称点F恰好落在边OC上时,求此时反比例函数的表达式.
(考试时间120分钟,满分150分)
一、选择题(本大题共10小题,每小题4分,共40分)
1.下列函数中,y是x的反比例函数的是( )
A. B. C.y=-3x D.
2.下列选项中,反比例函数的图象一定经过的点是( )
A.(1,4) B.(-1,-4) C.(-2,2) D.(2,2)
3.若反比例函数在每一个象限内y的值都随x值的增大而增大,则k的值可能是
( )
A.-3 B.-1 C.0 D.
4.若A(x1,-6),B(x2,-2),C(x3,3)都在反比例函数的图象上,则x1,x2,x3的大小关系为
( )
A.x3
A.(2,2) B.(-2,-1) C.(-2,-2) D.(-1,-4)
6.近视眼镜的度数y(度)与镜片焦距x(米)之间具有如图所示的反比例函数关系.小明原来佩戴400度的近视眼镜,经过一段时间的矫正治疗,复查验光时,所配镜片焦距调整为0.4米,则小明的眼镜度数( )
A.下降了150度 B.下降了250度 C.下降了350度 D.不变
7.如图,点A在反比例函数(x<0)的图象上,点B在反比例函数(x>0)的图象x上,连接AB,与y轴交于点C,且AB∥x轴,BC=2AC,D是x轴正半轴上一点,连接AD,BD,则△ABD的面积为( )
A.3 B. C. D.
8.在同一平面直角坐标系中,反比例函数与一次函数y=ax+b的图象可能是( )
9.在平面直角坐标系中,将一块含45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )
A.(,0) B.(2,0) C.(,0) D.(3,0)
10.如图,四边形OABC是平行四边形,对角线OB在y轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线和的一支上,过点A,C分别作x轴的垂线,垂足为M,N,有以下的结论:①阴影部分的面积为(k1+k2);②若点B的坐标为(0,6),点A的坐标为(2,2),则k2=-8;③当∠AOC=90°时,|k1|=|k2|;④当OA=OC时,两双曲线关于y轴对称.其中正确的结论是( )
A.①②③④⑤ B.②③④ C.①②③ D.②④
二、填空题(本大题共5小题,每小题4分,共20分)
11.若反比例函数的图象过第二、四象限,则常数m的取值范围是______.
12.由电源、开关、滑动变阻器及若干导线组成的串联电路中,已知电源电压为定值,闭合开关后,改变滑动变阻器的阻值R(始终保持R>0),发现通过滑动变阻器的电流I与滑动变阻器的电阻R成反比例函数关系,它的图象如图所示,若要使得通过滑动变阻器的电流I不超过4A,则滑动变阻器阻值R的取值范围是______.
13.如图,反比例函数(1≤x≤4)的图象记为曲线C1,将C1向左平移2个单位长度,得到曲线C2,则C1平移至C2所扫过的面积为____.
14.如图,在平面直角坐标系中,△OAB和△BCD都是等腰直角三角形,且∠OAB=∠BCD=90°,点B,D都在x轴上,点A,C都在反比例函数(x>0)的图象上,则点C的级坐标为______.
15.如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3=…,过点A1,A2,A3,…分别作x轴的垂线与反比例函数(x>0)的图象交于点P1,P3,P3,…,得到△OP1A1,△A1P2A2,△A2P3A3,…,并设其面积分别为S1,S2,S3,…,以此类推,则S2023的值为____.
三、解答题(本大题共10小题,共90分)
16.(7分)反比例函数的图象如图所示:
(1)求a的取值范围;
(2)若A(-1,m),B(-2,n)是该函数图象上的两点,比较m,n的大小.
17.(8分)如图,根据小孔成像的科学原理,当像距(小孔到像的距离)和物高(蜡烛火焰高度)不变时,火焰的像高y(单位:cm)是物距(小孔到蜡烛的距离)x(单位:cm)的反比例函数,当x=6时,y=2.
(1)求y关于x的函数表达式;
(2)若火焰的像高为3cm,求小孔到蜡烛的距离.
18.(8分)已知y=y1+y2,y1与x成正比例,y2与x成反比例,且当x=-1时,y=5;当x=2时,y=-4.求y与x之间的函数关系式.
19.(8分)如图,在平面直角坐标系中,反比例函数(k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,若△AOB的面积为5.
(1)求k和m的值;
(2)当x≥8时,求函数值y的取值范围.
20.(8分)如图,在平面直角坐标系中,点A的坐标为(-6,4),反比例函数(k≠0)的图象经过OA的中点B,AD⊥y轴于点D,且交反比例函数图象于点C,连接BC,求四边形OBCD的面积.
21.(9分)如图①,将一长方体A放置于一水平玻璃桌面上,按不同的方式摆放,记录桌面所受压强p(Pa)与受力面积S(m2)的关系如下表所示:
(1)求桌面所受压强p(Pa)与受力面积S(m2)之间的函数表达式;
(2)现将另一长、宽、高分别为0.2m,0.3m,0.2m的长方体B按图②所示的方式放置于该水平玻璃桌面上,若桌面所受压强p(Pa)与受力面积S(m2)之间的关系满足(1)中的函数表达式,且该玻璃桌面能承受的最大压强为5000 Pa,请你判断这种摆放方式是否安全?并说明理由.
22.(9分)如图,在平面直角坐标系中,△OAC的边OC在y轴上,反比例函数(x>0)的图象经过点A和点B(2,6),且B为AC的中点.
(1)求k的值和点C的坐标;
(2)求△OAC的周长.
23.(10分)在平面直角坐标系中,一次函数y=2x+b的图象与x轴的交点为A(2,0),与y轴的交点为B,直线AB与反比例函数的图象交于点C(-1,m).
(1)求一次函数和反比例函数的表达式;
(2)求关于x的不等式2x+b>的解集;
(3)P是反比例函数图象上的点,过点P作PM⊥x轴,垂足为M,连接OP,BM,当S△ABM=2S△OMP时,求点P的坐标.
(11分)某数学活动小组在研究反比例函数图象与几何图形的位置关系时,经历了如下过程:如图①,正方形ABCD在平面直角坐标系的第一象限,AB∥x轴,AD∥y轴,A(m,n),AB=a
(1)数学思考:若存在一个反比例函数(k≠0)的图象同时经过点B,D,则m与n之间的x
数量关系为______.
(2)数学应用:①若A(1,1),AB=2,反比例函数(k1≠0)的图象同时经过点B,D,则k1=______.
②在①的条件下,如图②,点E,F分别在BC,DC的延长线上,且CE=CF=1,若反比例函数(k2≠0)的图象同时经过点E,F,则k2=_______.
③在②的条件下,若点P,Q在反比例函数(k3≠0)的图象上,且四边形EFPQ是正方形,求k3的值.
25.(12分)如图①,在平面直角坐标系中,矩形OABC的边OC,OA分别在坐标轴上,且OA=3,0C=6,反比例函数(x>0)的图象与AB,BC分别交于点D,E,连接DE.
(1)如图②,连接OD,OE,当△OAD的面积为2时,
①k=______.
②求△ODE的面积;
(2)如图③,将△DEB沿DE翻折,当点B的对称点F恰好落在边OC上时,求此时反比例函数的表达式.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
