第二十三章 旋转 单元检测试题 2023--2024学年人教版九年级数学上册(含答案解析)
文档属性
| 名称 | 第二十三章 旋转 单元检测试题 2023--2024学年人教版九年级数学上册(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 414.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-12 19:04:32 | ||
图片预览

文档简介
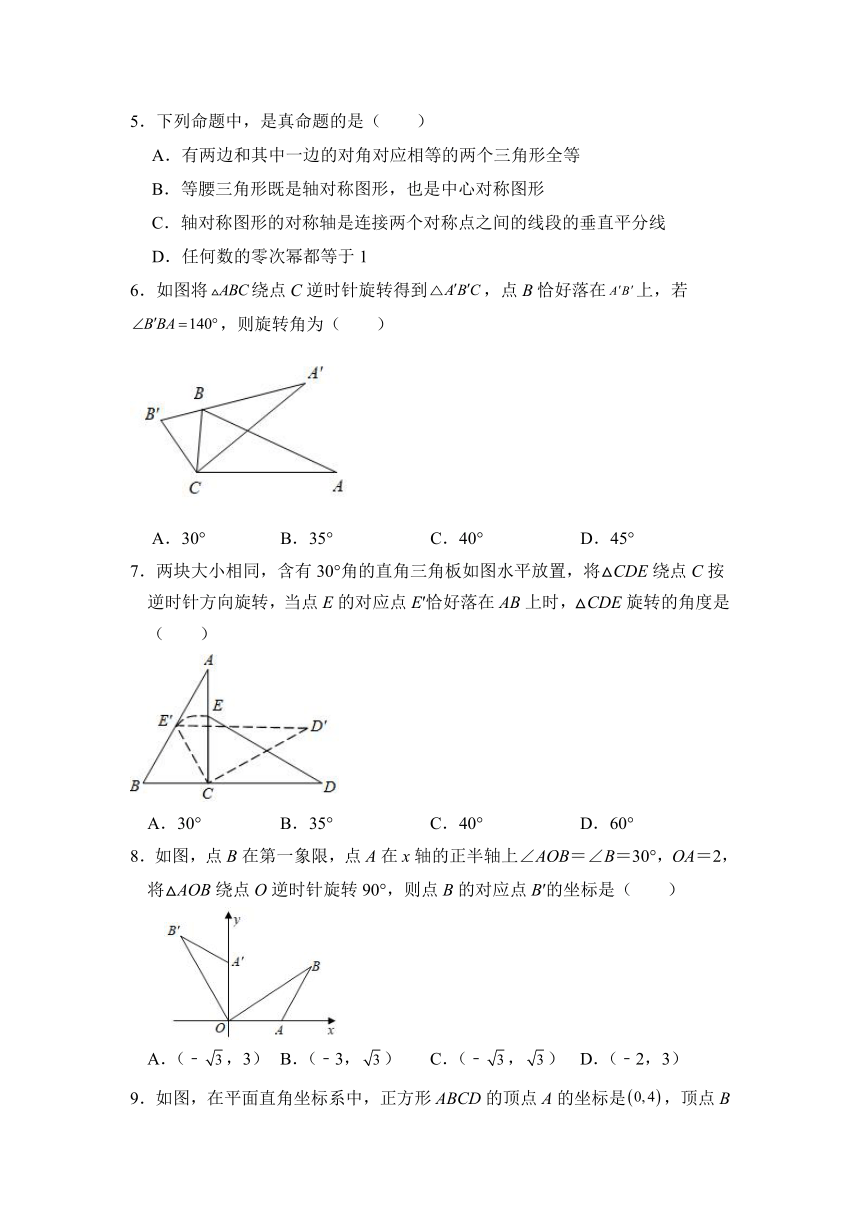
第二十三章 《旋转》单元测试卷
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分,共30分)
1.观察下列四个图案,它们分别绕中心旋转一定的角度后,都能和原来的图形重合,其中旋转的角度最大的是( )
A. B. C. D.
2.如图,将边长相等的正△ABP和正五边形ABCDE的一边AB重叠在一起,当△ABP绕着点A顺时针旋转α°时,顶点P刚好落在正五边形的对称轴EF上,此时α的值为( )
A.45 B.30 C.26 D.24
3.如图,点A、O、B在一条直线上,,OD平分,现将OC以每秒5°的速度绕点O顺时针旋转一周,OD保持不动.当时,OC的运动时间为( )
A.5秒 B.31秒 C.5秒或41秒 D.5秒或67秒
4.已知点坐标为,把点绕着坐标原点逆时针旋转,点对应点为,那么点的坐标是( )
A. B. C. D.
5.下列命题中,是真命题的是( )
A.有两边和其中一边的对角对应相等的两个三角形全等
B.等腰三角形既是轴对称图形,也是中心对称图形
C.轴对称图形的对称轴是连接两个对称点之间的线段的垂直平分线
D.任何数的零次幂都等于1
6.如图将绕点C逆时针旋转得到,点B恰好落在上,若,则旋转角为( )
A.30° B.35° C.40° D.45°
7.两块大小相同,含有30°角的直角三角板如图水平放置,将△CDE绕点C按逆时针方向旋转,当点E的对应点E′恰好落在AB上时,△CDE旋转的角度是( )
A.30° B.35° C.40° D.60°
8.如图,点B在第一象限,点A在x轴的正半轴上∠AOB=∠B=30°,OA=2,将△AOB绕点O逆时针旋转90°,则点B的对应点B′的坐标是( )
A.(﹣,3) B.(﹣3,) C.(﹣,) D.(﹣2,3)
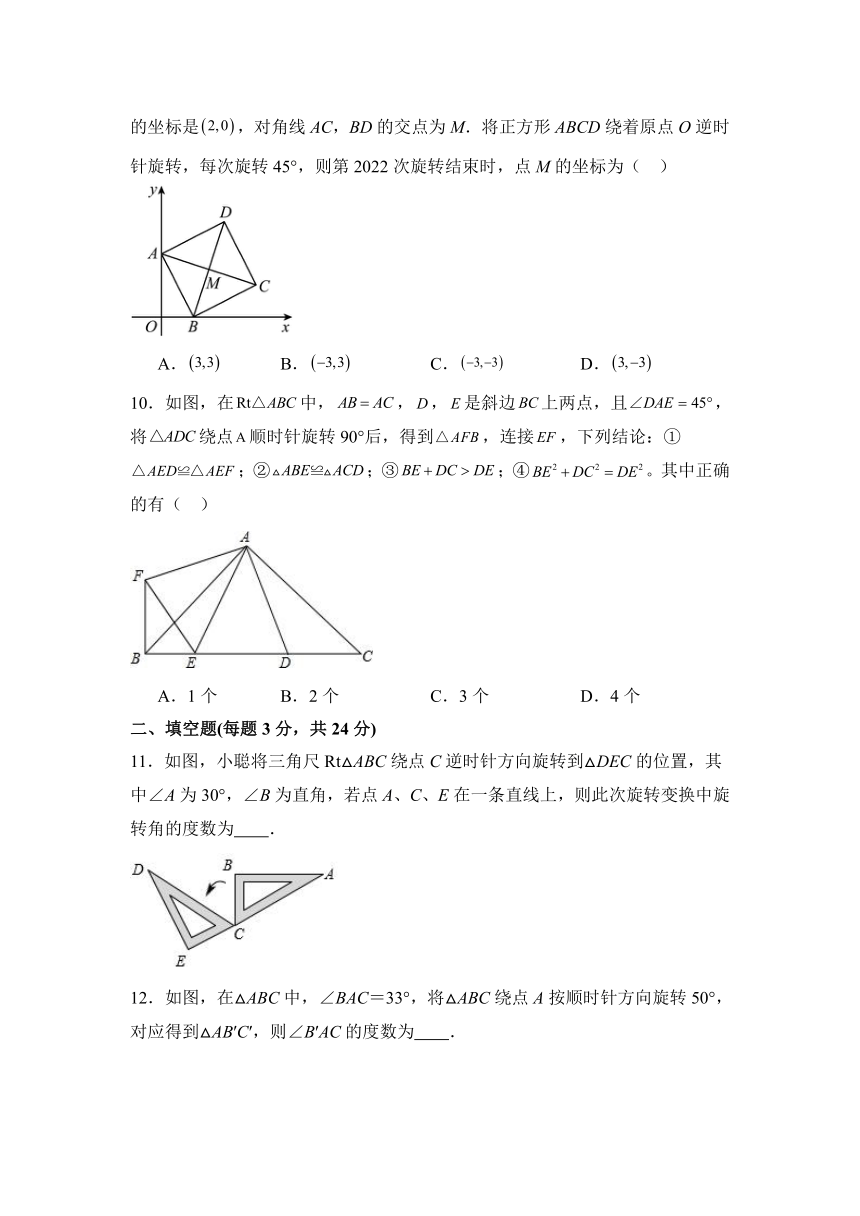
9.如图,在平面直角坐标系中,正方形ABCD的顶点A的坐标是,顶点B
的坐标是,对角线AC,BD的交点为M.将正方形ABCD绕着原点O逆时针旋转,每次旋转45°,则第2022次旋转结束时,点M的坐标为( )
A. B. C. D.
10.如图,在中,,,是斜边上两点,且,将绕点顺时针旋转90°后,得到,连接,下列结论:①;②;③;④。其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每题3分,共24分)
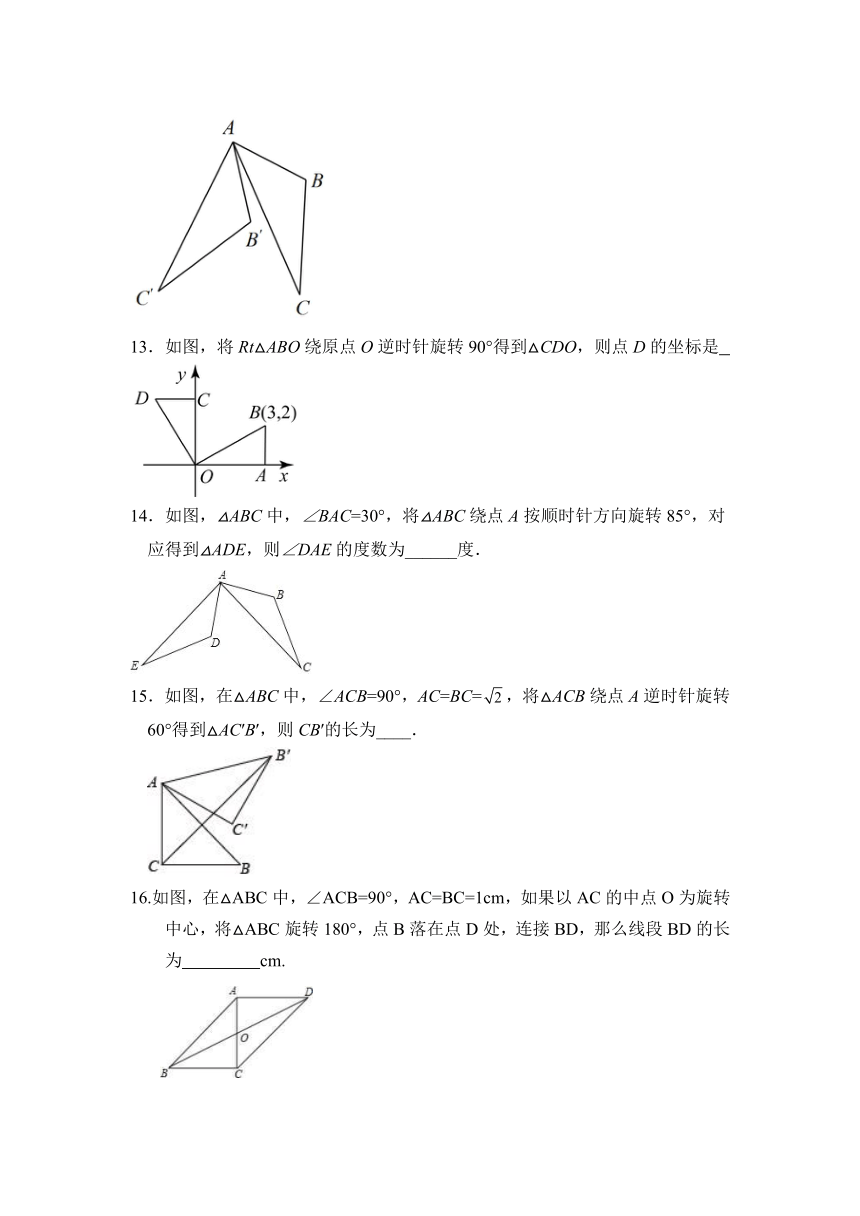
11.如图,小聪将三角尺Rt△ABC绕点C逆时针方向旋转到△DEC的位置,其中∠A为30°,∠B为直角,若点A、C、E在一条直线上,则此次旋转变换中旋转角的度数为 .
12.如图,在△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,则∠B′AC的度数为 .
13.如图,将Rt△ABO绕原点O逆时针旋转90°得到△CDO,则点D的坐标是
14.如图,△ABC中,∠BAC=30°,将△ABC绕点A按顺时针方向旋转85°,对应得到△ADE,则∠DAE的度数为______度.
15.如图,在△ABC中,∠ACB=90°,AC=BC=,将△ACB绕点A逆时针旋转60°得到△AC′B′,则CB′的长为____.
16.如图,在△ABC中,∠ACB=90°,AC=BC=1cm,如果以AC的中点O为旋转中心,将△ABC旋转180°,点B落在点D处,连接BD,那么线段BD的长为 cm.
17.如图,在直角坐标系中,已知点的坐标为,将线段按逆时针方向旋转,再将其长度伸长为的倍,得到线段;又将线段按逆时针方向旋转,长度伸长为的倍,得到线段......如此下去,得到线段为正整数),则点的坐标为 .
18.如图,是正方形内一点,,,,则 °.正方形的面积是 .
三.解答题(共46分,19题6分,20 ---24题8分)
19.如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置.
(1)旋转中心是点 ,旋转角度是 度;
(2)若连结EF,则△AEF是 三角形;并证明
20.△ABC在平面直角坐标系xoy中的位置如图所示.
(1)作△ABC关于点C成中心对称的(点A,B,C的对应点分别是点)
(2)将向右平移4个单位长度,作出平移后的 (点的对应点分别是点)
(3)在x轴上求作一点,使的值最小,并写出点P的坐标(不写解答过程,直接写出结果)
21.如图,四边形ABCD是正方形,△ADF绕着点A顺时旋转90°得到△ABE,若AF=4,AB=7.
(1)求DE的长度;
(2)指出BE与DF的关系如何?并说明由.
22.如图,已知:如图点,点在轴正半轴上,且,将线段绕点沿顺时针旋转,设点旋转后的对应点是点,求点的坐标.
23.四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.
(1)求证:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE绕旋转中心 点,按顺时针方向旋转 度得到;
(3)若BC=8,DE=6,求△AEF的面积.
24.如图,直线MN∥PQ,将一副三角板中的两块直角三角板如图1放置,∠ACB=∠EDF=90°,∠ABC=∠BAC=45°,∠DFE=30°,∠DEF=60°,此时点A与点E重合.
(1)对于图1,固定△ABC的位置不变,将△DEF绕点E按顺时针方向进行旋转,旋转至DE与BC首次平行,如图2所示,求此时∠FAC的度数.
(2)对于图1,固定△ABC的位置不变,将△DEF沿AC方向平移至点F正好落在直线MN上,再将△DEF绕点F按顺时针方向进行旋转,如图3所示.
①若边EF与边BC交于点G,试判断∠BGF﹣∠EFN的值是否为定值,若是定值,则求出该定值,若不是定值,请说明理由;
②对于图3,固定△ABC的位置不变,将△DEF绕点F顺时针方向以每秒5°的速度进行旋转,当EF与直线MN首次重合时停止运动,当经过t秒时,线段DE与△ABC的一条边平行,求满足条件的t的值.
参考答案
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A D C D B D A A D C
二、填空题(每题3分,共24分)
11.120°
12.17°
13.(-2,3)
14.30.
15.
16.答案为:.
17.
18.
三.解答题(共46分,19题6分,20 ---24题8分)
19.(1)A;90;(2)△AEF是等腰直角三角形,
20.(1)(2)略
(3)(,0)
21.(1)3;(2)BE=DF,BE⊥DF.
【详解】
解:(1)∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴AE=AF=4,AD=AB=7,
∴DE=AD﹣AE=7﹣4=3;
(2)BE、DF的关系为:BE=DF,BE⊥DF.理由如下:
∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴△ABE≌△ADF,
∴BE=DF,∠ABE=∠ADF,
∵∠ADF+∠F=180°﹣90°=90°,
∴∠ABE+∠F=90°,
∴BE⊥DF,
∴BE、DF的关系为:BE=DF,BE⊥DF.
22.点的坐标为.
【详解】
解:如图,作轴于,
∵,,
∴,
∵线段绕点沿逆时针旋转得,
∴,且,
∴
而,
∴,
在和中
,
∴,
∴,,
∴,
∴点的坐标为.
20.【答案】(1)证明:∵四边形ABCD是正方形,∴AD=AB,∠D=∠ABC=90°.
又∵点F是CB延长线上的点,∴∠ABF=90°.
在△ADE和△ABF中,∵ ,
∴△ADE≌△ABF(SAS).
(2)A;90
(3)∵BC=8,∴AD=8.
在Rt△ADE中,DE=6,AD=8,∴ .
∵△ABF可以由△ADE绕旋转中心 A点,按顺时针方向旋转90 度得到,
∴AE=AF,∠EAF=90°.
∴△AEF的面积= AE2= ×100=50(平方单位).
21.【答案】(1)解:如图,
∵DEBC
∴∠CED=∠BCA=90°
∴∠FAC=∠CED-∠FAD=90°-60°=30°
(2)解:①是,45°.理由如下:
过点G作直线HLMN,则HLPQ.
∴∠HGF=∠EFN,∠BGH=∠ABC,
∴∠BGF=∠HGF+∠BGH=∠EFN+∠ABC
∴∠BGF-∠EFN=∠ABC=45°
②共分三种情况:
情况1:DEBC时,5t=30,t=6;
情况2:DEAB时,5t=75,t=15;
情况3:DEAC时,5t=120,t=24.
∴综上,t=6,15,24秒.
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分,共30分)
1.观察下列四个图案,它们分别绕中心旋转一定的角度后,都能和原来的图形重合,其中旋转的角度最大的是( )
A. B. C. D.
2.如图,将边长相等的正△ABP和正五边形ABCDE的一边AB重叠在一起,当△ABP绕着点A顺时针旋转α°时,顶点P刚好落在正五边形的对称轴EF上,此时α的值为( )
A.45 B.30 C.26 D.24
3.如图,点A、O、B在一条直线上,,OD平分,现将OC以每秒5°的速度绕点O顺时针旋转一周,OD保持不动.当时,OC的运动时间为( )
A.5秒 B.31秒 C.5秒或41秒 D.5秒或67秒
4.已知点坐标为,把点绕着坐标原点逆时针旋转,点对应点为,那么点的坐标是( )
A. B. C. D.
5.下列命题中,是真命题的是( )
A.有两边和其中一边的对角对应相等的两个三角形全等
B.等腰三角形既是轴对称图形,也是中心对称图形
C.轴对称图形的对称轴是连接两个对称点之间的线段的垂直平分线
D.任何数的零次幂都等于1
6.如图将绕点C逆时针旋转得到,点B恰好落在上,若,则旋转角为( )
A.30° B.35° C.40° D.45°
7.两块大小相同,含有30°角的直角三角板如图水平放置,将△CDE绕点C按逆时针方向旋转,当点E的对应点E′恰好落在AB上时,△CDE旋转的角度是( )
A.30° B.35° C.40° D.60°
8.如图,点B在第一象限,点A在x轴的正半轴上∠AOB=∠B=30°,OA=2,将△AOB绕点O逆时针旋转90°,则点B的对应点B′的坐标是( )
A.(﹣,3) B.(﹣3,) C.(﹣,) D.(﹣2,3)
9.如图,在平面直角坐标系中,正方形ABCD的顶点A的坐标是,顶点B
的坐标是,对角线AC,BD的交点为M.将正方形ABCD绕着原点O逆时针旋转,每次旋转45°,则第2022次旋转结束时,点M的坐标为( )
A. B. C. D.
10.如图,在中,,,是斜边上两点,且,将绕点顺时针旋转90°后,得到,连接,下列结论:①;②;③;④。其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每题3分,共24分)
11.如图,小聪将三角尺Rt△ABC绕点C逆时针方向旋转到△DEC的位置,其中∠A为30°,∠B为直角,若点A、C、E在一条直线上,则此次旋转变换中旋转角的度数为 .
12.如图,在△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,则∠B′AC的度数为 .
13.如图,将Rt△ABO绕原点O逆时针旋转90°得到△CDO,则点D的坐标是
14.如图,△ABC中,∠BAC=30°,将△ABC绕点A按顺时针方向旋转85°,对应得到△ADE,则∠DAE的度数为______度.
15.如图,在△ABC中,∠ACB=90°,AC=BC=,将△ACB绕点A逆时针旋转60°得到△AC′B′,则CB′的长为____.
16.如图,在△ABC中,∠ACB=90°,AC=BC=1cm,如果以AC的中点O为旋转中心,将△ABC旋转180°,点B落在点D处,连接BD,那么线段BD的长为 cm.
17.如图,在直角坐标系中,已知点的坐标为,将线段按逆时针方向旋转,再将其长度伸长为的倍,得到线段;又将线段按逆时针方向旋转,长度伸长为的倍,得到线段......如此下去,得到线段为正整数),则点的坐标为 .
18.如图,是正方形内一点,,,,则 °.正方形的面积是 .
三.解答题(共46分,19题6分,20 ---24题8分)
19.如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置.
(1)旋转中心是点 ,旋转角度是 度;
(2)若连结EF,则△AEF是 三角形;并证明
20.△ABC在平面直角坐标系xoy中的位置如图所示.
(1)作△ABC关于点C成中心对称的(点A,B,C的对应点分别是点)
(2)将向右平移4个单位长度,作出平移后的 (点的对应点分别是点)
(3)在x轴上求作一点,使的值最小,并写出点P的坐标(不写解答过程,直接写出结果)
21.如图,四边形ABCD是正方形,△ADF绕着点A顺时旋转90°得到△ABE,若AF=4,AB=7.
(1)求DE的长度;
(2)指出BE与DF的关系如何?并说明由.
22.如图,已知:如图点,点在轴正半轴上,且,将线段绕点沿顺时针旋转,设点旋转后的对应点是点,求点的坐标.
23.四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.
(1)求证:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE绕旋转中心 点,按顺时针方向旋转 度得到;
(3)若BC=8,DE=6,求△AEF的面积.
24.如图,直线MN∥PQ,将一副三角板中的两块直角三角板如图1放置,∠ACB=∠EDF=90°,∠ABC=∠BAC=45°,∠DFE=30°,∠DEF=60°,此时点A与点E重合.
(1)对于图1,固定△ABC的位置不变,将△DEF绕点E按顺时针方向进行旋转,旋转至DE与BC首次平行,如图2所示,求此时∠FAC的度数.
(2)对于图1,固定△ABC的位置不变,将△DEF沿AC方向平移至点F正好落在直线MN上,再将△DEF绕点F按顺时针方向进行旋转,如图3所示.
①若边EF与边BC交于点G,试判断∠BGF﹣∠EFN的值是否为定值,若是定值,则求出该定值,若不是定值,请说明理由;
②对于图3,固定△ABC的位置不变,将△DEF绕点F顺时针方向以每秒5°的速度进行旋转,当EF与直线MN首次重合时停止运动,当经过t秒时,线段DE与△ABC的一条边平行,求满足条件的t的值.
参考答案
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A D C D B D A A D C
二、填空题(每题3分,共24分)
11.120°
12.17°
13.(-2,3)
14.30.
15.
16.答案为:.
17.
18.
三.解答题(共46分,19题6分,20 ---24题8分)
19.(1)A;90;(2)△AEF是等腰直角三角形,
20.(1)(2)略
(3)(,0)
21.(1)3;(2)BE=DF,BE⊥DF.
【详解】
解:(1)∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴AE=AF=4,AD=AB=7,
∴DE=AD﹣AE=7﹣4=3;
(2)BE、DF的关系为:BE=DF,BE⊥DF.理由如下:
∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴△ABE≌△ADF,
∴BE=DF,∠ABE=∠ADF,
∵∠ADF+∠F=180°﹣90°=90°,
∴∠ABE+∠F=90°,
∴BE⊥DF,
∴BE、DF的关系为:BE=DF,BE⊥DF.
22.点的坐标为.
【详解】
解:如图,作轴于,
∵,,
∴,
∵线段绕点沿逆时针旋转得,
∴,且,
∴
而,
∴,
在和中
,
∴,
∴,,
∴,
∴点的坐标为.
20.【答案】(1)证明:∵四边形ABCD是正方形,∴AD=AB,∠D=∠ABC=90°.
又∵点F是CB延长线上的点,∴∠ABF=90°.
在△ADE和△ABF中,∵ ,
∴△ADE≌△ABF(SAS).
(2)A;90
(3)∵BC=8,∴AD=8.
在Rt△ADE中,DE=6,AD=8,∴ .
∵△ABF可以由△ADE绕旋转中心 A点,按顺时针方向旋转90 度得到,
∴AE=AF,∠EAF=90°.
∴△AEF的面积= AE2= ×100=50(平方单位).
21.【答案】(1)解:如图,
∵DEBC
∴∠CED=∠BCA=90°
∴∠FAC=∠CED-∠FAD=90°-60°=30°
(2)解:①是,45°.理由如下:
过点G作直线HLMN,则HLPQ.
∴∠HGF=∠EFN,∠BGH=∠ABC,
∴∠BGF=∠HGF+∠BGH=∠EFN+∠ABC
∴∠BGF-∠EFN=∠ABC=45°
②共分三种情况:
情况1:DEBC时,5t=30,t=6;
情况2:DEAB时,5t=75,t=15;
情况3:DEAC时,5t=120,t=24.
∴综上,t=6,15,24秒.
同课章节目录
