(尖子生培优)数学广角-数与形应用题(提高)-六年级上册数学专项培优卷(人教版)(带解析)
文档属性
| 名称 | (尖子生培优)数学广角-数与形应用题(提高)-六年级上册数学专项培优卷(人教版)(带解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 633.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-11 17:09:35 | ||
图片预览

文档简介
数学广角-数与形应用题(提高)
六年级上册数学期中培优卷(人教版)
一.应用题(共58小题)
1.图中的涂色部分表示312.整个图形表示多少?
2.1、4、7、10、13、…这个数列中,有6个连续数字的和是159,那么这6个数中最小的是几?
3.如图,第二个图形是由第一个图形连接三边中点而得到的,第三个图形是由第二个图形中间的一个三角形连接三边中点而得到的,以此类推……分别写出第二个图形、第三个图形和第四个图形中的三角形个数.如果第n个图形中的三角形个数为8057,n是多少?
4.五(1)班进行团体操表演,排成下面的队形.如果再增加一些人,但是保持点阵的规律不变,至少增加多少人?
5.海豹是生活在海洋中的哺乳动物,它们一般靠肺呼吸,所以必须经常不断地浮到海面呼吸空气。一只海豹6时开始从海底经过9分钟慢慢浮到海面,然后浮出海面呼吸2分钟,最后再经过9分钟回到海底,这样有规律地进行这个过程。7时整海豹会在什么位置?(请你用喜欢的方式表示出你的思考过程和结果)
6.用小棒按照如图的方式摆图形.
(1)摆1个五边形需要 根小棒,摆2个五边形需要 根小棒,摆3个五边形需要 根小棒.
(2)照这样摆下去,
①摆5个五边形需要多少根小棒?摆10个呢?
②用61根小棒可以摆出多少个五边形?
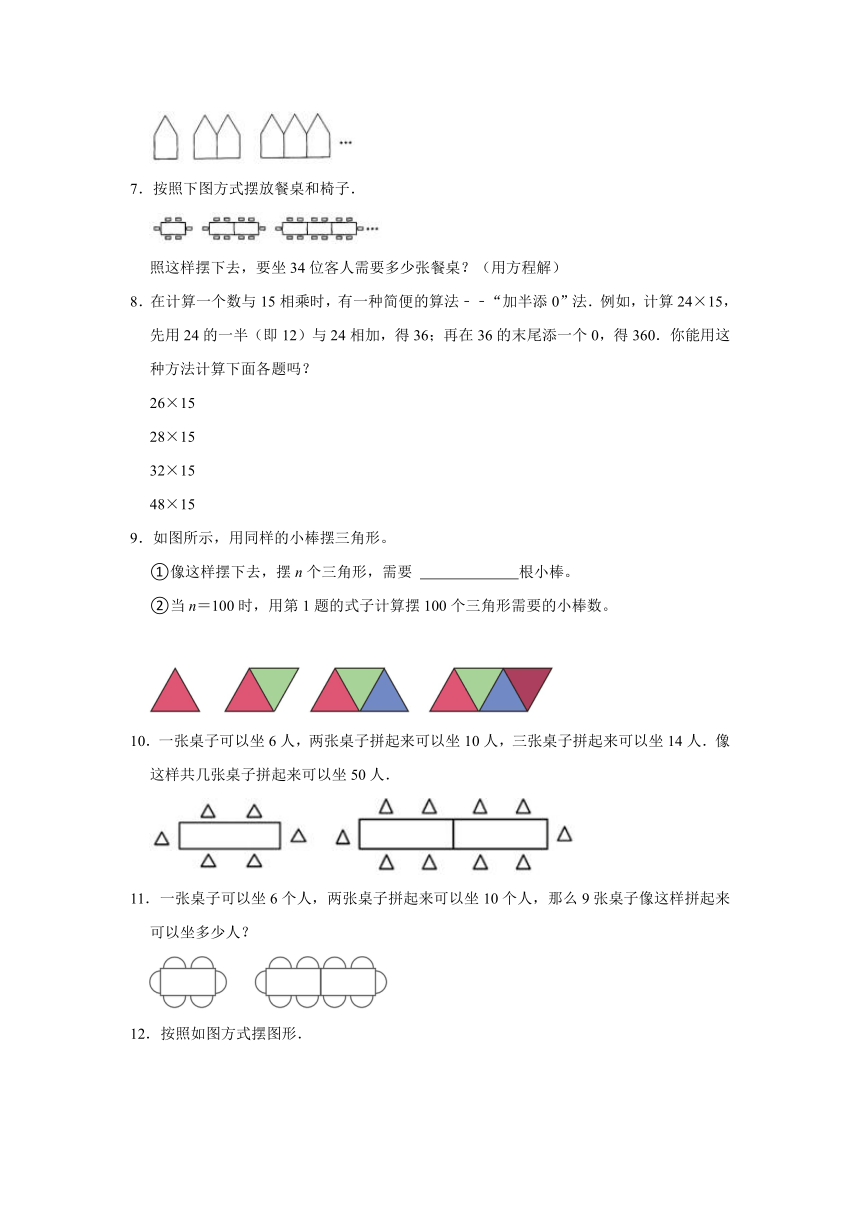
7.按照下图方式摆放餐桌和椅子.
照这样摆下去,要坐34位客人需要多少张餐桌?(用方程解)
8.在计算一个数与15相乘时,有一种简便的算法﹣﹣“加半添0”法.例如,计算24×15,先用24的一半(即12)与24相加,得36;再在36的末尾添一个0,得360.你能用这种方法计算下面各题吗?
26×15
28×15
32×15
48×15
9.如图所示,用同样的小棒摆三角形。
①像这样摆下去,摆n个三角形,需要 根小棒。
②当n=100时,用第1题的式子计算摆100个三角形需要的小棒数。
10.一张桌子可以坐6人,两张桌子拼起来可以坐10人,三张桌子拼起来可以坐14人.像这样共几张桌子拼起来可以坐50人.
11.一张桌子可以坐6个人,两张桌子拼起来可以坐10个人,那么9张桌子像这样拼起来可以坐多少人?
12.按照如图方式摆图形.
(1)照这样,摆第15个图形需要用多少根小棒?
(2)如果摆出的图形用了21根小棒,那么摆到了第几个图形?
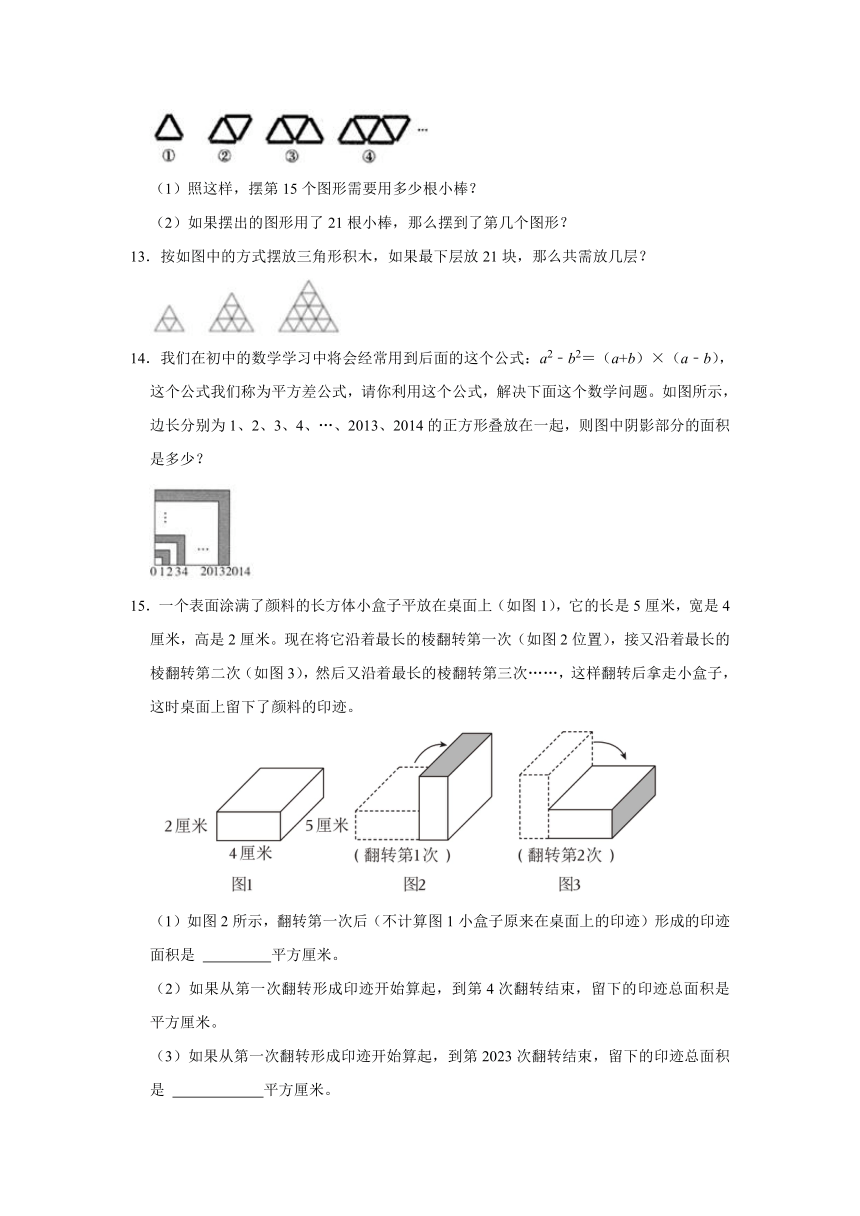
13.按如图中的方式摆放三角形积木,如果最下层放21块,那么共需放几层?
14.我们在初中的数学学习中将会经常用到后面的这个公式:a2﹣b2=(a+b)×(a﹣b),这个公式我们称为平方差公式,请你利用这个公式,解决下面这个数学问题。如图所示,边长分别为1、2、3、4、…、2013、2014的正方形叠放在一起,则图中阴影部分的面积是多少?
15.一个表面涂满了颜料的长方体小盒子平放在桌面上(如图1),它的长是5厘米,宽是4厘米,高是2厘米。现在将它沿着最长的棱翻转第一次(如图2位置),接又沿着最长的棱翻转第二次(如图3),然后又沿着最长的棱翻转第三次……,这样翻转后拿走小盒子,这时桌面上留下了颜料的印迹。
(1)如图2所示,翻转第一次后(不计算图1小盒子原来在桌面上的印迹)形成的印迹面积是 平方厘米。
(2)如果从第一次翻转形成印迹开始算起,到第4次翻转结束,留下的印迹总面积是 平方厘米。
(3)如果从第一次翻转形成印迹开始算起,到第2023次翻转结束,留下的印迹总面积是 平方厘米。
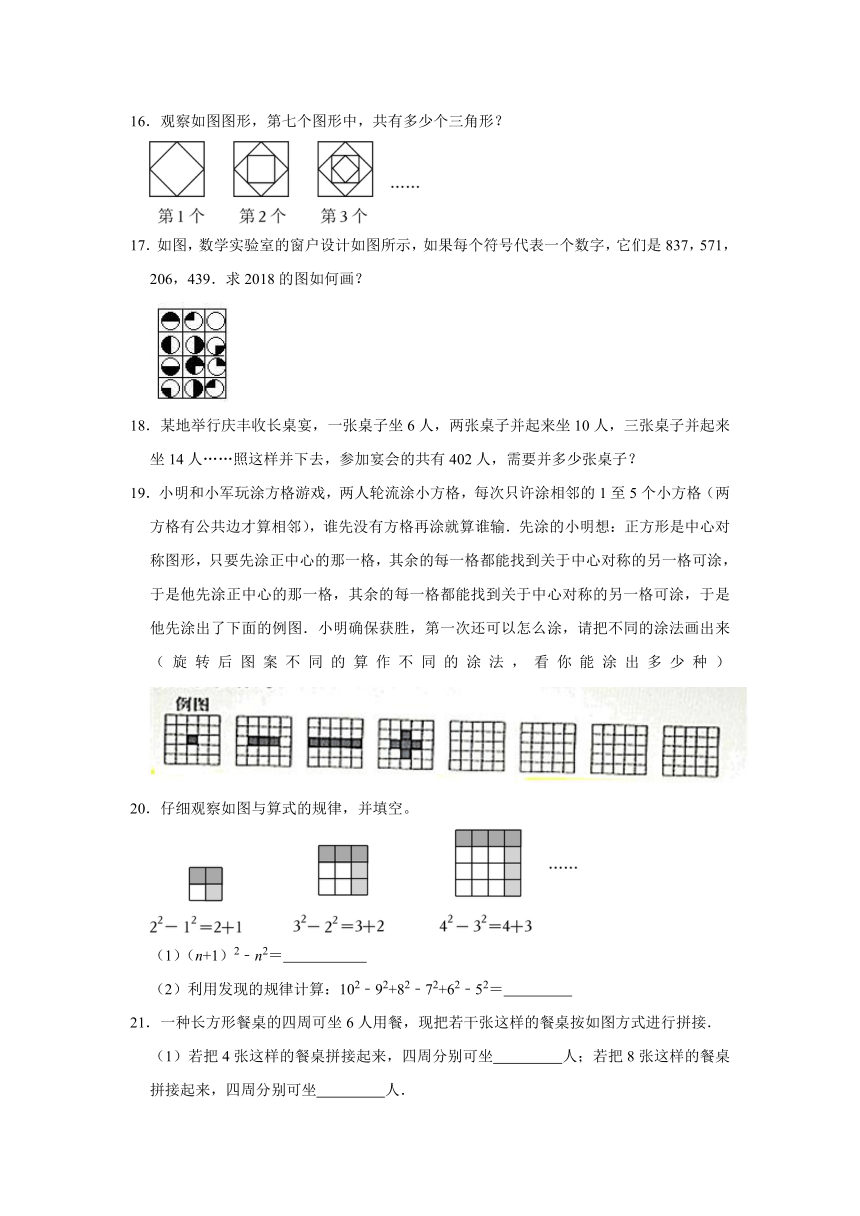
16.观察如图图形,第七个图形中,共有多少个三角形?
17.如图,数学实验室的窗户设计如图所示,如果每个符号代表一个数字,它们是837,571,206,439.求2018的图如何画?
18.某地举行庆丰收长桌宴,一张桌子坐6人,两张桌子并起来坐10人,三张桌子并起来坐14人……照这样并下去,参加宴会的共有402人,需要并多少张桌子?
19.小明和小军玩涂方格游戏,两人轮流涂小方格,每次只许涂相邻的1至5个小方格(两方格有公共边才算相邻),谁先没有方格再涂就算谁输.先涂的小明想:正方形是中心对称图形,只要先涂正中心的那一格,其余的每一格都能找到关于中心对称的另一格可涂,于是他先涂正中心的那一格,其余的每一格都能找到关于中心对称的另一格可涂,于是他先涂出了下面的例图.小明确保获胜,第一次还可以怎么涂,请把不同的涂法画出来(旋转后图案不同的算作不同的涂法,看你能涂出多少种)
20.仔细观察如图与算式的规律,并填空。
(1)(n+1)2﹣n2=
(2)利用发现的规律计算:102﹣92+82﹣72+62﹣52=
21.一种长方形餐桌的四周可坐6人用餐,现把若干张这样的餐桌按如图方式进行拼接.
(1)若把4张这样的餐桌拼接起来,四周分别可坐 人;若把8张这样的餐桌拼接起来,四周分别可坐 人.
(2)若用餐的人数有90人,则这样的餐桌需要多少张?
22.按照前两组的规律填数,你知道第三组的“?”处应该填几吗?
23.将图1边长为9厘米的等边三角形的每一个边长三等分,然后变化出图2所示的图形,求多边形的周长.
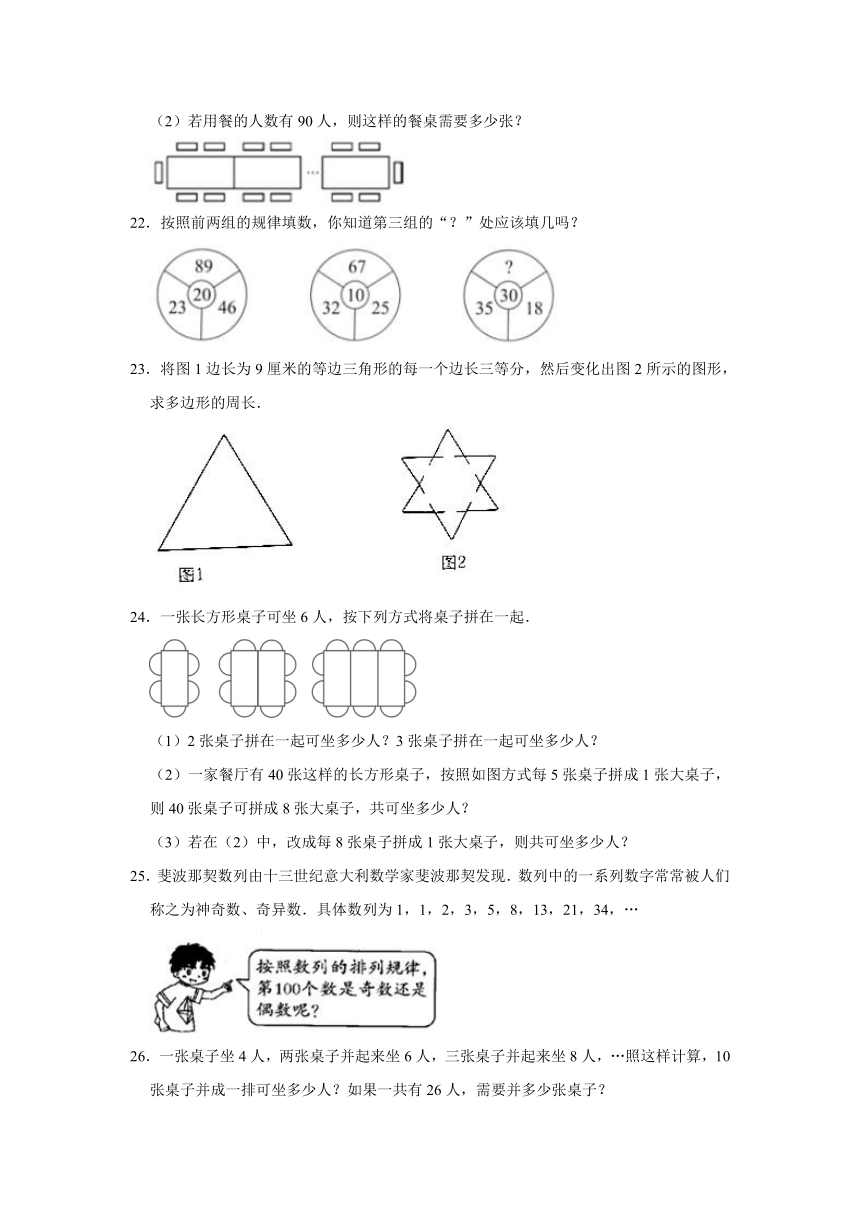
24.一张长方形桌子可坐6人,按下列方式将桌子拼在一起.
(1)2张桌子拼在一起可坐多少人?3张桌子拼在一起可坐多少人?
(2)一家餐厅有40张这样的长方形桌子,按照如图方式每5张桌子拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐多少人?
(3)若在(2)中,改成每8张桌子拼成1张大桌子,则共可坐多少人?
25.斐波那契数列由十三世纪意大利数学家斐波那契发现.数列中的一系列数字常常被人们称之为神奇数、奇异数.具体数列为1,1,2,3,5,8,13,21,34,…
26.一张桌子坐4人,两张桌子并起来坐6人,三张桌子并起来坐8人,…照这样计算,10张桌子并成一排可坐多少人?如果一共有26人,需要并多少张桌子?
27.把5张图画像如图这样钉在墙上,一共要用多少个图钉?
28.(如图所示)用小棒按下图摆六边形:摆1个六边形需要5+1=6根小棒,摆2个六边形需要2×5+1=11根小棒,摆3个六边形需要3×5+1=16根小棒,…
①像这样摆下去,摆m个六边形一共需要多少根小棒?(请用含有字母m的式子表示)
②当m=10时,用第①题的式子计算摆10个六边形一共需要多少根小棒?
29.用绿、白两种颜色的小方块瓷砖400块贴成一正方向墙面,这个墙面最外层铺的是白色瓷砖.由外到内的第二层是绿色瓷砖,第三层是白色瓷砖,第四层又是绿色…,那么,这个墙面上绿色瓷砖共有多少块?
30.小华把一些珠子放在桌子上的15个盒子中,已知盒子中的珠子数按盒子从左往右的顺序成一个等差数列,任一盒子中不止两颗珠子,并且从左数第8个盒子中有24颗珠子.请问:这15个盒子中一共有多少颗珠子?
31.如图里的数和它周围3个里的数有关系。想一想,里应当填什么数?应当填 。
用算式表示你的想法:
因为: 、
所以:
32.杨辉三角,是中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现的一种几何排列.你能计算图中的杨辉三角中一共有多少个数字吗?
33.用一根长96cm的绳子在地上摆正方形.当这根绳子摆出48个正方形时,正方形的边长是多少厘米?顶点有几个?
34.快乐提升:
如图,摆一个三角形用3根小棒,增加2根,可以摆出一个平行四边形,继续增加2根,摆出一个梯形,照这样摆下去,21根小棒能摆出一个什么样的图形?51根呢?
35.某饭店的餐桌都是能坐4人的正方形,当团体客人在10人以上时,饭店允许客人将餐桌拼成一长条,但每张桌子不能有空位,问如果团体客人是22人,那么需要几张桌子?
36.先观察前三题计算结果,再直接写出最后两题的得数。
0.1+0.11=0.21
0.1+0.11+0.111=0.321
0.1+0.11+0.111+0.1111=0.4321
0.1+0.11+0.111+0.1111+…+0.1111111=
0.1+0.11+0.111+0.1111+…+0.111111111=
37.用小棒按下面的方式拼图形.
(1)如果按下面的规律拼成5个这样的五边形,一共要用 根小棒.
五边形
个数 拼成的形状 小棒根数
1 5
2 9
3 13
4 17
(2)接着拼下去,一共用了57根小棒,你知道一共拼成了多少个五边形吗?
38.一串数:,,,,,,,,,,……
(1)第800个数是多少?
(2)是第几个数?
(3)前552个数的和是多少?
(4)前n个数的和能否等于106,如果能,试求出n的值,如果不能,试说明理由.
39.用6根同样长的小棒可以摆成一个正六边形(如图①),再接着摆下去(如图②、③、④),图⑧一共需要多少根小棒?
40.笑笑用水果卡片摆成下面的“T”字,照这样摆下去,第10个“T”字要用多少张水果卡片?
41.用正方形硬纸板做三棱柱盒子,每个盒子由3个举行侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面;B方法:剪4个侧面和5个底面
现有19章硬纸板,裁剪时x张用A方法,其余用B方法
(1)用x的代数式分别表示出裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做出多少个盒子?
42.用小棒摆三角形如图:
摆1个三角形要用3根小棒,摆2个三角形要用5根小棒,摆3个三角形要用7根小棒,摆4个三角形要用9根小棒。
(1)照这样,摆5个三角形要用 根小棒,摆6个三角形要用 根小棒。
(2)照这样摆下去,摆20个三角形要用 根小棒。摆n个三角形要用 根小棒.(用含有n的算式表示)
43.如图摆放餐桌和椅子:
(1)一张餐桌可坐6人,两张餐桌可以坐10人,四张餐桌可坐多少人?
(2)按照这个规律摆放,m张餐桌可以坐多少人?
(3)按照这个规律摆放餐桌,要坐42人,需要多少张餐桌?
44.观察点阵图形,找出规律.
(1)第8个图形中有多少个点?
(2)第n个图形中有多少个点?
45.10月1日小时姐姐带领大家去旅游,来到一块形状是等边三角形的果园,它的边长是54米,三边及内部都植满了石榴树;每棵树之间均相距6米,各个顶点上都植有一棵;小时姐姐给同学们分工,每两位同学栽一棵,正好分完.聪明的你知道小时姐姐共带了多少名同学吗?
46.已知摆1个三角形需要3根小棒,摆2个三角形需要5根小棒,摆3个三角形需要7根……按照这样的规律,摆15个三角形需要多少根小棒?用79根小棒可以摆多少个三角形?
47.如图是由边长为1的正方形按照某种规律排列而成的。
(1)观察图形,填写下表。
图形 ① ② ③
正方形的个数 8 18
图形的周长
(2)推测第n个图形中,正方形的个数为 ,周长为 。
48.任意写一个四位数(各个数位上的数字互不相同),将这个四位数的四个数字重新组合,求出其中最大的数与最小的数的差,再将得到的差像上面那样重新组合,重复这个过程,你发现了什么?
49.如图,1个杯子的高度是15cm,把5个完全一样的杯子叠起来的高度是25cm,那么10个这样的杯子叠起来的高度是多少厘米?
50.观察下图中图形的规律,图形?应该是
A.B.C.D.E.F.
51.找规律在空格或括号里填上适当的数.
52.海安某步行街要铺设一条人行道,人行道长400米,宽1.6米.现在用边长都是0.4米的红、黄两种正方形地砖铺设(如图是铺设的局部图示).
(1)请帮忙算一算,铺设这条人行道一共需多少块地砖?(不计损耗)
(2)铺设这条人行道一共需要多少块红色地砖?(不计损耗)
53.有一本漫画书共27页,插图和文字按页排列为文、文、图、图、图、文、文、图、图、图、文……照这样计算,这本书共有多少页插图?
54.一张长方形桌子可以坐6个人,按照下图的方式摆放桌椅。
(1)像这样摆下去,x张桌子可以坐多少人?
(2)当x=15时,一共可以坐多少人?
(3)像这样,摆多少张桌子可以坐60人?
55.佳佳摆小棒(如图),照这样摆下去,第5个图形有多少根小棒?第8个呢?
56.如图1,在长方形ABCD中,点E从点A开始,以每秒3厘米的速度沿长方形的边AB、BC、CD匀速移动。随着点E的移动,三角形ADE的面积会不断发生变化。它的面积变化情况如图2所示。
(1)点E从点A开始移动, 秒后到达点B。
(2)图2中3秒到8秒表示点E在长方形的边 上移动。
(3)长方形ABCD的面积是多少?
57.如图是由同型号黑白两种颜色的三角形瓷砖按一定规律铺设的图形.
(1)请在虚线框内画出第4个图形.(只要画出示意图)
(2)第10个图形中有 块黑色的瓷砖.
58.一个五边形需要5根小棒,那么搭4个五边形,需要几根小棒?
数学广角-数与形应用题(提高)
六年级上册数学期中培优卷(人教版)
参考答案与试题解析
一.应用题(共58小题)
1.【答案】见试题解答内容
【分析】在这里是把一个正方形的面积看作单位“1”,把它平均分成8份,每份是它的,其中1份涂色,表示,即这个正方形的表示312,根据分数除法的意义,用312除以8就是整个图形表示的数,或根据整数乘法的意义,用312乘8就是或个图形所表示的数.
【解答】解:3122496
或312×8=2496
答:整个图形表示2496.
【点评】解答此题的关键是明白涂色部分占整个图形的.
2.【答案】见试题解答内容
【分析】据题意可知,这个数列是公差为3的等差数列,由此可设这6个数中最小的数为x,则后边5个数与第一个数的差分别为3,6,…15,又因为有6个连续数的和是159,据此可得等量关系式:x+(x+3)+…+(x+15)=159,解此方程即得这6个数中最小的是多少.
【解答】解:设这6个数中最小的数为x,据题意可得方程:
x+(x+3)+…+(x+15)=159
6x+(3+6+…+15)=159
6x+45=159
6x=114
x=19
答:这6个数中最小的是19.
【点评】根据数列的排列规律及已知条件列出等量关系式是完成本题的关键.
3.【答案】见试题解答内容
【分析】根据图示,发现其规律为:第一个图形中三角形个数:1个;第二个图形中三角形个数:1×4+1=5(个);第三个图形中三角形个数:2×4+1=9(个);第四个图形中三角形个数:3×4+1=13(个);第n个图形中三角形个数:(n﹣1)×4+1=(4n﹣3)(个),计算n的值即可.
【解答】解:第一个图形中三角形个数:1个;
第二个图形中三角形个数:1×4+1=5(个);
第三个图形中三角形个数:2×4+1=9(个);
第四个图形中三角形个数:3×4+1=13(个);
第n个图形中三角形个数:
(n﹣1)×4+1=(4n﹣3)(个)
4n﹣3=8057,n=2015.
答:n是第2015个图形.
【点评】本题主要考查数与形结合的规律,关键根据所给图示发现图示排列的规律,并运用规律做题.
4.【答案】见试题解答内容
【分析】观察图形可知,这个点阵是个正方形的,每天边上都是3人,若再增加一些人,但是保持点阵的规律不变,则每条边上至少是4人,由此时人数减去原来的人数即可解答问题.
【解答】解:根据题干分析可得:4×4﹣3×3
=16﹣9
=7(人)
答:至少增加7人.
【点评】主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.
5.【答案】海底。
【分析】根据题意,6时到7时是1小时,为60分钟;海豹完成一次从海底到海面再回到海底的过程是需要9+2+9=20(分钟),据此计算解答即可。
【解答】解:6时到7时是1小时,为60分钟;
海豹完成一次从海底到海面再回到海底的过程是需要9+2+9=20(分钟);
60÷20=3(次),
即60分钟的时间,海豹正好可以完成3次海底到海面再回到海底的过程;7时整,海豹刚好回到海底。
故答案为:海底。
【点评】本题考查规律探究问题,根据整个过程所用时间计算即可。
6.【答案】见试题解答内容
【分析】(1)根据图示可知,摆一个五边形需要5根小棒,摆2个五边形需要9根小棒,也可以写成5+4×1=9(根)小棒,摆3个五边形需要13根小棒,也可以写成5+4×2=13(根)小棒…以后每增加一个五边形,需要的小棒个数就会增加4根,由此可得摆n个五边形需要5+4(n﹣1)=4n+1根小棒.
(2)①根据(1)中推理的推论,摆5个五边形需要4×5+1=21根小棒,摆10个五边形需要4×10+1=41根小棒.
②根据(1)中的推理的推论,设4n+1=61,可求出n的值既是所需摆出的五边形的个数.
【解答】解:(1)根据图示可知,摆1个五边形需要5根小棒,摆2个五边形需要5+4×1=9(根)小棒,
摆3个五边形需要5+4×2=13(根)小棒.
(2)①根据(1)中推理可得:摆n个五边形需要5+4(n﹣1)=4n+1根小棒,
摆5个五边形为:4×5+1=21(根),则摆5个五边形需要21根小棒;
摆10个五边形为:4×10+1=41(根),则摆10个五边形需要41根小棒.
②当4n+1=61时,可得4n=60,最终解得:n=15,所以用61根小棒可以摆出15个五边形.
故答案为:5,9,13.
【点评】本题考查了图形变化类,解决本题的关键是观察图形找到规律,并最终进行求解.
7.【答案】见试题解答内容
【分析】观察摆放的桌子,不难发现:在1张桌子坐6人的基础上,多1张桌子,多4人;设有n张桌子:
n=1时,可坐6人,可以写成4×1+2;
n=2时,可坐10人,可以写成4×2+2;
n=3时,可坐14人,可以写成4×3+2;
…;
所以n张桌子可坐(4n+2)人.
由此规律可得方程:4n+2=34;然后列方程解答即可.
【解答】解:设有n张桌子,
4n+2=34
4n=32
n=8
答:要坐34位客人需要8张餐桌.
【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,设未知数为n,由此列方程解决问题.
8.【答案】见试题解答内容
【分析】根据巧算的方法:“加半添0”法解答即可.
【解答】解:26÷2+26=39
所以26×15=390
28÷2+28=42
所以28×15=420
32÷2+32=48
所以32×15=480
48÷2+48=72
所以48×15=720
【点评】解答此题的关键是找出算式之间数与数的关系,得出规律,再根据规律解决问题.
9.【答案】①2n+1;②201根。
【分析】①由图可以看出摆一个三角形用3根小棒,摆两个三角形用5根小棒,摆三个三角形用7根小棒,摆四个三角形用9根小棒……,所以摆n个三角形用(2n+1)根小棒。
②把n=100代入2n+1,即可求出摆100个三角形需要的小棒数。
【解答】解:①一个三角用2×1+1=3(根)
二个三角形用2×2+1=5(根)
三个三角形用2×3+1=7(根)
四个三角形用2×4+1=9(根)
……
n个三角形用(2n+1)根
答:摆n个三角形需(2n+1)根小棒
②当n=100时
2n+1
=2×100+1
=200+1
=201(根)
答:摆100个三角形需要201根小棒。
故答案为:2n+1。
【点评】此题主要是初步渗透不完全归纳思想和代数思想,培养符号化意识,提高抽象和概括能力,关键是找规律,找到规律,代入数值计算比较简单。
10.【答案】见试题解答内容
【分析】由一张桌子坐6人,两张桌子坐10人,三张桌子坐14人,可以发现每多一张桌子多4个人,由此用字母表示这一规律,然后代值计算.
【解答】解:1张桌子可坐2×1+4=6人,
2张桌子拼在一起可坐2×4+2=10人,
3张桌子拼在一起可坐4×3+2=14人,
…
所以五张桌子坐4×5+2=22人,
…
那么n张桌子坐(4n+2)人.
当共有50人时,
4n+2=50
4n=48
n=12
答:这样共12张桌子拼起来可以坐50人.
【点评】此题考查图形的变化规律,找出规律,利用规律解决问题.
11.【答案】38。
【分析】由一张桌子坐6人,两张桌子坐10人,三张桌子坐14人,可以发现每多一张桌子多4个人,由此用字母表示这一规律,然后代值计算。
【解答】解:1张桌子可坐2×1+4=6(人)
2张桌子拼在一起可坐2×4+2=10(人)
3张桌子拼在一起可坐4×3+2=14(人)
…
所以五张桌子坐4×5+2=22(人)
…
那么n张桌子坐(4n+2)人
当n=9时,
4×9+2
=36+2
=38(人)
答:这样共9张桌子拼起来可以坐38人。
【点评】此题考查图形的变化规律,找出规律,利用规律解决问题。
12.【答案】见试题解答内容
【分析】(1)摆1个三角形所需小棒的根数=3,2个三角形所需小棒的根数=3+2,3个三角形所需小棒的根数=3+2×2,…,于是得到n个三角形所需小棒的根数=3+2×(n﹣1)=2n+1,然后把n=15代入计算即可;
(2)根据上面得出的规律,可得如果摆出的图形用了21根小棒,即2n+1=21,据此求出n的值即可解答问题.
【解答】解:(1)1个三角形所需小棒的根数=3
2个三角形所需小棒的根数=3+2
3个三角形所需小棒的根数=3+2×2
…
所以n个三角形所需小棒的根数=3+2×(n﹣1)=2n+1
当n=15时,2n+1=2×15+1=31(根)
答:像这样摆下去第15个图摆了31个三角形.
(2)总根数=21时
2n+1=21
2n=22
n=11
答:如果用了21根小棒,他摆了18个三角形.
【点评】本题考查了规律型:图形的变化类,通过从一些特殊的图形变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.
13.【答案】11.
【分析】根据图示可知:1层最下层有1块;2层最下层有3块;3层最下层有5块;……最下层有21块,层数为:(21+1)÷2=11(层)。据此解答。
【解答】解:根据分析,最下层放21块,层数为:
(21+1)÷2
=22÷2
=11(层)
答:一共需要放11层.
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力.
14.【答案】2029105。
【分析】根据所给图示可知,该阴影部分的面积为:(20142﹣20132)+(20122﹣20112)+……+(42﹣32)+(22﹣12)。利用平方差公式计算即可。
【解答】解:(20142﹣20132)+(20122﹣20112)+……+(42﹣32)+(22﹣12)
=(2014+2013)(2014﹣2013)+(2012+2011)(2012﹣2011)+……+(4+3)(4﹣3)+(2+1)(2﹣1)
=2014+2013+2012+2011+……+4+3+2+1
=1007×2015
=2029105
答:阴影部分的面积是2029105。
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和应用公式解决问题的能力。
15.【答案】10,100,30340。
【分析】由题干中的长方体可知,上下两个面大小相等,左右两个侧面相等,前后两个面相等。第一层1次翻转后右侧面向下,第2次翻转后上面向下,第3次翻转后左侧面向下,第4次翻转后下面向下……据此分析解答。
【解答】解:(1)5×2=10(平方厘米)
如图2所示,翻转第一次后(不计算图1小盒子原来在桌面上的印迹)形成的印迹面积是10平方厘米。
(2)4÷2=2(个)
(4×5+2×5)×2
=30×2
=60(平方厘米)
答:如果从第一次翻转形成印迹开始算起,到第4次翻转结束,留下的印迹总面积是60平方厘米。
(3)2023÷4=505(个)……3(次)
60×505+4×5+5×2×2
=30300+20+20
=30340(平方厘米)
答:如果从第一次翻转形成印迹开始算起,到第2023次翻转结束,留下的印迹总面积是30350平方厘米。
故答案为:10,100,30340。
【点评】解决本题的关键是理解每次翻转后那个面向下,结合长方形的面积公式,分析解答即可。
16.【答案】见试题解答内容
【分析】根据图示,发现这组图形的规律:第一个图形三角形个数:4个,第二个图形三角形个数:4×2=8(个);第三个图形三角形个数:4×3=12(个);……第n个图形三角形的个数:4n个.据此解题.
【解答】解:第一个图形三角形个数:4个
第二个图形三角形个数:4×2=8(个)
第三个图形三角形个数:4×3=12(个)
……
第n个图形三角形的个数:4n个
所以第七个图形三角形的个数:
4×7=28(个)
答:第七个图形三角形共有28个.
【点评】本题主要考查数与形结合的规律,关键根据所给图形,发现其规律,并运用规律做题.
17.【答案】见试题解答内容
【分析】观察图案和数据可知:837,439第2位都是3,观察图形可知,只有第2行和第4行是这两个数,第2行和第4行的末尾数字图形是7或者9,而571是其中一个数,第1行和第3行只有第一行的第2个图形是前面的那个7或9,所以第1行的数字是571,第2行是439,第3行是206,第4行是837,据此即可得出代表1995的符号.
【解答】解:由图案和提供的数据可知:837,439第2位都是3,所以只有第2行和第4行是这两个数,第2行和第4行的末尾数字图形是7或者9,而571是其中一个数,第1行和第3行只有第一行的第2个图形是前面的那个7或9,所以第1行的数字是571,第2行是439,第3行是206,第4行是837;
即0,1,2,3,4,5,6,7,8,9分别用符号:
2018是:
【点评】本题考查了用符号(窗户形状)代表阿拉伯数码,解题的关键是由相同的数字得出对应的图案,找到突破口.
18.【答案】100张。
【分析】根据题意发现:一张桌子坐6人,每多1张桌子就多坐4人,则拼n张桌子,能坐(4n+2)个人;据此逆推即可。
【解答】解:(402﹣2)÷4
=400÷4
=100(张)
答:需要并100张桌子。
【点评】本题考查了图形的变化类题目,认真观察、分析和归纳总结是解决此题的关键。
19.【答案】见试题解答内容
【分析】整个图形是中心对称图形,先涂的仍旧涂出一个以正方形中心为对称点的中心对称图形,接下来,无论小军怎么涂,小明都可以在对称的位置上涂,确保获胜.
【解答】解:小明仍旧涂出一个以正方形中心为对称点的中心对称图形即可,如图:
【点评】本题主要考查了学生灵活解决生活中实际问题的能力,本题以正方形中心为对称点是解题关键.
20.【答案】2n+1;45。
【分析】根据仔细观察如图与算式的规律,可知(n+1)2﹣n2=2n+1;利用发现的规律,102﹣92+82﹣72+62﹣52=(102﹣92)+(82﹣72)+(62﹣52),然后结合规律解答即可。
【解答】解:(1)(n+1)2﹣n2=2n+1。
(2)利用发现的规律计算:
102﹣92+82﹣72+62﹣52
=(102﹣92)+(82﹣72)+(62﹣52)
=10+9+8+7+6+5
=45
答:(1)(n+1)2﹣n2=2n+1。
(2)利用发现的规律计算:102﹣92+82﹣72+62﹣52=45。
故答案为:2n+1;45。
【点评】本题考查了算式的规律,首先仔细观察如图与算式,找出规律,然后结合题意分析解答即可。
21.【答案】见试题解答内容
【分析】观察图形发现:一种长方形餐桌的四周可坐6人用餐,多一个长方形餐桌,多用4个人,则第n张餐桌,需要可坐(2+4n)人.
【解答】解:根据分析可得,
第n张餐桌,需要可坐(2+4n)人.
(1)2+4×4=18(人)
2+4×8=34(人)
答:若把4张这样的餐桌拼接起来,四周分别可坐 18人.若把8张这样的餐桌拼接起来,四周分别可坐34人.
(2)2+4n=90
4n=88
n=22
答:若用餐的人数有90人,则这样的餐桌需要22张.
故答案为:18,34.
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力.
22.【答案】
【分析】左下角、右下角以及中间这三个数的和等于最上面那个数,据此求解即可。
【解答】解:35+18+30
=53+30
=83
【点评】解答此题的关键是,根据所给出的数列的数的特点,找出规律,再根据规律解决问题。
23.【答案】见试题解答内容
【分析】根据周长的意义,围成图形一周的长度叫做周长;在此题中等边三角形的边长为9厘米,变化出图2所示的图形的边长可求为3厘米,共12条边,用一条边的长度乘以12即可求解.
【解答】解:9÷3=3(厘米)
3×12=36(厘米)
答:多边形的周长是36厘米.
【点评】本题主要考查了周长的意义,即围成图形一周的长度叫做周长.
24.【答案】(1)8,10;(2)112;(3)100.
【分析】(1)根据图示2张桌子拼一起,可以坐:6+2=8(人),3张桌子拼一起,可以坐:6+2+2=10(人).
(2)先根据(1)的规律,计算5张桌子拼一起,可以坐的人数:6+2+2+2+2=14(人),再计算40张桌子可以拼成几个大桌子,然后乘14,计算可坐人数.
(3)根据规律计算8张桌子拼一起,可以坐的人数:6+2+2+2+……+2=6+2×(8﹣1)=20(人),然后计算40张桌子可以拼成几个大桌子,乘20就是一共可坐的人数.
【解答】解:(1)6+2=8(人)
6+2+2=10(人)
答:2张桌子拼在一起可坐8人;3张桌子拼在一起可坐10人.
(2)6+2+2+2+2=14(人)
8×14=112(人)
答:共可坐112人.
(3)6+2+2+2+2+2+2+2
=6+2×(8﹣1)
=6+14
=20(人)
40÷8×20
5×20
=100(人)
答:改成每8张桌子拼成1张大桌子,则共可坐100人.
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力.
25.【答案】见试题解答内容
【分析】观察数列的奇偶性发现:第1、2个数是奇数,第3个数是偶数;第4、5个数是奇数,第6个数是偶数……,每三个数看成一组,每组的前两个数是奇数,第三个数是偶数,用100除以3,求出商和余数,再根据余数进行判断,由此求解.
【解答】解:100÷3=33……1
余数是1,所以第100个数是第34个循环的第1个数,是奇数.
答:第100个数是奇数.
【点评】解决这类问题关键是把重复出现的部分看成一组,根据除法的意义,求出总数量里面有多少个这样的一组,还余几,然后根据余数进行推算.
26.【答案】见试题解答内容
【分析】观察摆放的桌子,不难发现:在1张桌子坐4人的基础上,多1张桌子,多2人.由此规律即可解决问题.
【解答】解:(1)n=1时,可坐4人,可以写成2×1+2
n=2时,可坐6人,可以写成2×2+2
n=3时,可坐8人,可以写成2×3=2
…
所以当n=10时,可坐2×10+2=22人
答:10张桌子并成一排可坐22人.
(2)2n+2=26
2n=24
n=12
答:如果有26人,需要12张桌子.
【点评】主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.
27.【答案】18。
【分析】由图可知,所需要的图钉为上、中、下3排,每排6个,每排的个数乘排数即为要用的图钉总数,据此解答。
【解答】解:6×3=18(个)
答:一共要用18个图钉。
【点评】本题考查了学生对于图形的观察能力,由图读出相关信息是解决此题的关键。
28.【答案】①(5m+1)根;
②51根。
【分析】①摆1个六边形需要5+1=6根小棒,摆2个六边形需要2×5+1=11根小棒,摆3个六边形需要3×5+1=16根小棒,……,摆m个六边形需要小棒:(5m+1)根。
②把m=10时,代入①中的公式,计算即可。
【解答】解:①摆1个六边形需要5+1=6根小棒
摆2个六边形需要2×5+1=11根小棒
摆3个六边形需要3×5+1=16根小棒
……
摆m个六边形需要小棒:(5m+1)根
答:摆m个六边形一共需要(5m+1)根小棒。
②当m=10时,
5×10+1
=50+1
=51(根)
答:摆10个六边形一共需要51根小棒。
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力。
29.【答案】见试题解答内容
【分析】因为正方形墙共用100块小方砖网贴成,设每块小方砖为1个面积单位,则正方形墙的面积为100个面积单位,边长为20个长度单位,每块小方砖的边长为1个长度单位.由题意可知,由外到内,最外层(白方砖)的边长为20个长度单位,第二层(绿方砖)边长为18个长度单位,第三层(白方砖)边长为16个长度单位,第四层(绿方砖)边长为14个长度单位……由此可知,由外到里,绿色方砖的边长分别为18、14、10、6、2.由此即可计算出绿方砖的块数.
【解答】解:由外到内绿方砖是第二层、第四层、第站层……(偶数层)
第二层边长为18个长度单位,方砖块数为:18×2+(18﹣2)×2=36+32=68(块)
第四屋边长为14个长度单位,方砖块数为14×2+(14﹣2)×2=28+24=52(块)
第六层边长为10个长度单位,方砖块数为10×2+(10﹣2)×2=20+16=36(块)
第八层边长为6个长度单位,方砖块数为6×2+(6﹣2)×2=12+8=20(块)
第十层(也是最内层)边长是2个长度单位,方砖块数为2×2+(2﹣2)×2=4+0=4(块)
68+52+36+20+4=180(块)
答:这个墙面上绿色瓷砖共有180块.
【点评】此题可通过画图找出每层绿色方砖与层数之间的关系,求出每层绿色方砖的块数,进而求出一共用绿色方砖的块数.
30.【答案】见试题解答内容
【分析】15个盒子中的珠子从左到右是一个项数为15的等差数列,其中第8个盒子中的珠子数为中间项,根据等差数列的意义,与中间项相邻的左、右两项之和等于中间项,与中间项相隔1项的左、右两项之和也等于中间项……因此,这15项之和就是等于中间项乘中间项数.
【解答】解:24×15=360(颗)
答:这15个盒子中一共有360颗珠子.
【点评】解答此题的关键是明白:与中间项相邻的左、右两项之和等于中间项,与中间项相隔1项的左、右两项之和也等于中间项……
31.【答案】3,里的数等于它周围3个的数的和,10=6+1+3,=3。
【分析】根据图示发现:里的数等于它周围3个里的数的和。据此解答。
【解答】解:因为:里的数等于它周围3个的数的和、10=6+1+3
所以:=3
故答案为:3,里的数等于它周围3个的数的和,10=6+1+3,=3。
【点评】通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力。
32.【答案】见试题解答内容
【分析】经过观察发现,这些数字组成的三角形是等腰三角形,两腰上的数都是1,第1行有1个数字,第2行有2个数字,第,3行有3个数字,…,一共10行,有1+2+3+4+5+6+7+8+9+10=55(个)数字,据此解答即可.
【解答】解:根据分析可知:
1+2+3+4+5+6+7+8+9+10=55(个)
答:图中的杨辉三角中一共有55个数字.
【点评】本题考查了数与形结合的变化规律,主要培养学生的观察能力和总结能力.
33.【答案】见试题解答内容
【分析】根据图示,发现这组图形的规律:第一个图形:正方形个数:1个,顶点个数:4个,边长:96÷4=24(厘米);第二个图形:正方形个数:2个,顶点个数:4+3=7(个),边长:96÷(4×2)=12(厘米);第三个图形,正方形个数:3个,顶点个数:4+3+3=10(个),边长:96÷(4×3)=8(厘米);……第n个图形正方形个数:n个,顶点个数:4+3(n﹣1)=(3n+1)个,边长:(96÷4n)厘米.据此解答.
【解答】解:第一个图形:正方形个数:1个,顶点个数:4个,边长:96÷4=24(厘米)
第二个图形:正方形个数:2个,顶点个数:4+3=7(个),边长:96÷(4×2)=12(厘米)
第三个图形,正方形个数:3个,顶点个数:4+3+3=10(个),边长:96÷(4×3)=8(厘米)
……
第n个图形正方形个数:n个,顶点个数:4+3(n﹣1)=(3n+1)个,边长:(96÷4n)厘米
由规律可知:
第48个图形的正方形个数为48个,
顶点个数为:
3×48+1
=144+1
=145(个)
边长:
96÷(4×48)
=96÷192
=0.5(厘米)
答:这根绳子摆出48个正方形时,正方形的边长是0.5厘米,顶点有145个.
【点评】本题主要考查数与形结合的规律,关键根据所给图形,发现其规律,并运用规律做题.
34.【答案】见试题解答内容
【分析】根据图示可知:摆1个三角形需要小棒:3根;摆2个三角形需要小棒:3+2=5(根);摆3个三角形需要小棒:3+2+2=7(根);……摆n个三角形需要小棒:3+2(n﹣1)=(2n﹣1)根.根据规律计算21、51根小棒可以摆几个三角形,进而判断其形状.
【解答】解:摆1个三角形需要小棒:3根
摆2个三角形需要小棒:3+2=5(根)
摆3个三角形需要小棒:3+2+2=7(根)
……
摆n个三角形需要小棒:3+2(n﹣1)=(2n﹣1)根
由图形可以知道:奇数个(1除外)三角形可以摆成梯形,偶数个三角形可以摆成平行四边形.
21根小棒摆三角形的个数:
2n﹣1=21
2n=22
n=11
11为奇数
51根小棒摆成三角形的个数:
2m﹣1=51
2m=52
m=26
26为偶数
答:21根小棒可以摆成梯形;51根小棒可以摆成平行四边形.
【点评】本题主要考查数与形结合的规律,关键根据图示发现其规律,并运用规律做题.
35.【答案】见试题解答内容
【分析】把餐桌拼成长条,如图:
1张桌子可坐:4人
2张桌子可坐:4+2=6(人)
3张桌子可坐:4+2+2=8(人)
……n张桌子可坐:
4+2(n﹣1)=(2n+2)人
由此求出当有22人时需要的桌子数量即可.
【解答】解:1张桌子可坐:4人
2张桌子可坐:4+2=6(人)
3张桌子可坐:4+2+2=8(人)
……n张桌子可坐:
4+2(n﹣1)=2n+2(人)
2n+2=22
2n+2﹣2=22﹣2
2n=20
n=10
答:需要10张桌子.
【点评】本题先画出图,结合图找出规律,再利用规律求解.
36.【答案】0.7654321;0.987654321。
【分析】通过观察:0.1+0.11=0.21
0.1+0.11+0.111=0.321
0.1+0.11+0.111+0.1111=0.4321
得出规律:得数看最后一个加数,如果最后一个加数的小数点后的有n(n≤9)个1,
得数的小数点后的数就从n依次从大到小排列到1,据此解答即可。
【解答】解:0.1+0.11=0.21
0.1+0.11+0.111=0.321
0.1+0.11+0.111+0.1111=0.4321
0.1+0.11+0.111+0.1111+…+0.1111111=0.7654321
0.1+0.11+0.111+0.1111+…+0.111111111=0.987654321
故答案为:0.7654321;0.987654321。
【点评】解决本题的关键是找出规律:得数看最后一个加数,如果最后一个加数的小数点后的有n(n≤9)个1,得数的小数点后的数就从n依次从大到小排列到1。
37.【答案】见试题解答内容
【分析】(1)由图示可知,拼1个五边形,需要小棒根数:5根;拼2个五边形,需要小棒根数:5+4=9(根);拼3个五边形,需要小棒根数:5+4+4=13(根);……有摆n个五边形,需要小棒根数:5+4×(n﹣1)=(4n+1)(根).根据规律计算即可.
(2)由(1)的规律可知,当4n+1=57时,n=14.
【解答】(1)拼1个五边形,需要小棒根数:5根
拼2个五边形,需要小棒根数:5+4=9(根)
拼3个五边形,需要小棒根数:5+4+4=13(根)
……
有拼n个五边形,需要小棒根数:5+4×(n﹣1)=(4n+1)(根)
当n=5时,所需小棒根数:
4×5+1
=20+1
=21(根)
答:拼成5个这样的五边形,一共要用 21根小棒.
(2)解:设一共拼成了x个五边形.
4x+1=57
4x=56
x=14
答:一共拼成了14个五边形.
故答案为:21.
【点评】本题主要考查数与形结合的规律,关键根据所给图示发现图示排列的规律,并运用规律做题.
38.【答案】(1);(2)第261个数或第285个数;(3)287.5;(4)存在前n个数的和等于106,此时n的值是201。
【分析】观察数列,,,,,,,,,,……,可发现:分母为1的分数有1个,分母为2的数有3个,分母为3的数有5个,所以可得出:分母为n的分数有2n﹣1个;分子都是从1开始到与分母的数字相同连续的自然数,再倒数回到1,由此规律解决问题:
(1)首先要计算第800个数之前最大的平方是:当n=28时,n2=784,第784个数是分母为28的最后一个数,所以可以找到第800个数;
(2)先找出分母是16的最后一个数,是第162个数,162=256,再向右数5个即可,因为同一个分母的数除中间为1的数是出现一次外,其余都是出现2次,所以倒数第5个数也是,得出结论;
(3)同(1)同理,先计算第552个数之前最大的平方数:当n=23时,n2=529,先计算分母为1至23的所有分数之和:1+2+3+……+23的值,再确定第529到552之间数的和,最后相加即可;
(4)因为分母为n的分数有2n﹣1个,且这2n﹣1个分数相加和为n;所以分母为n时,前n2个数的和为,确定当n为最大时,最接近106时的n=14,即前196个数的和为105,与106还相差1,分母为15的分数能否达到几个分数和为1,来判断。
【解答】解:观察数列,,,,,,,,,,……,可发现:分母为1的分数有1个,分母为2的数有3个,分母为3的数有5个,所以可得出:分母为n的分数有2n﹣1个;且这2n﹣1个分数相加和为n.;第12个是分母为1的最后一个,第22个是分母为2的最后一个……,第n2个是分母为n的最后一个;
(1)因为1+3+5+…+2n﹣1=n2,
所以令n2≤800,
解得:n≤28,
当n=28时,n2=784,
所以第784个数是分母为28的最后一个数,
所以800个数的分母为29,分子为800﹣784=16,所以第800个数为;
(2)因为162+5=256+5=261,
172﹣4=289﹣4=285,
所以是第261个数或第285个数;
(3)令n2≤552,
解得:n≤23,
当n=23时,n2=529,
即前529个数的和为:1+2+3+……+23=24×11+12=276,
第530至第552个数之间一共有:
552﹣530+1=23个数,
第530至第552个数的和为:
11.5,
所以前552个数的和是:276+11.5=287.5;
(4)分母为n时,前n2个数的和为,当n=14时,前142=196个数的和为:
105,
第197个数开始为分母是15的数:
1,
105+1=106,
所以存在前n个数的和等于106,此时n=196+5=201。
故答案为:(1);(2)第261个数或第285个数;(3)287.5;(4)存在前n个数的和等于106,此时n的值是201。
【点评】解决本题的关键是找出规律,解决问题。
39.【答案】见试题解答内容
【分析】摆1个六边形需要6根小棒,可以写作:5×1+1;摆2个需要11根小棒,可以写作:5×2+1;摆3个需要16根小棒,可以写成:5×3+1;…由此可以推理得出一般规律解答问题.
【解答】解:根据题干分析可得:摆1个六边形需要6根小棒,可以写作:5×1+1;
摆2个需要11根小棒,可以写作:5×2+1;
摆3个需要小棒:5×3+1=16;
摆n个需要小棒:5×n+1=5n+1;
当n=8时,5n+1=5×8+1=41;
答:图⑧一共需要41根小棒.
【点评】根据题干中已知的图形的排列特点及其数量关系,推理得出一般的结论进行解答,是此类问题的关键.
40.【答案】32张
【分析】第1个“T”用了5张水果卡片,第2个“T”用了8张水果卡片,第3个“T”用了11张水果卡片;5=3+2,8=3×2+2,11=3×3+2,所以第10个“T”字要用(3×10+2)张水果卡片。
【解答】解:3×10+2=32(张)
答:第10个“T”字要用32张水果卡片。
【点评】观察图形,探索图形的排列规律,根据图形中水果卡片的张数与项数的关系解决问题。
41.【答案】见试题解答内容
【分析】(1)由裁剪时x张用A方法,其余用(19﹣x)张就用B方法,据此即可分别表示出裁剪出的侧面和底面的个数;
(2)由侧面个数与底面个数比是3:2建立方程求出x的值,求出侧面的总数即可解答问题.
【解答】解:(1)因为裁剪时x张用A方法,所以剪裁时(19﹣x)张用B方法;
那么侧面的个数是:6x+4(19﹣x)=6x+76﹣4x=2x+76(个)
底面个数是:5(19﹣x)=95﹣5x(个)
(2)由题意可得:(2x+76):(95﹣5x)=3:@
解得x=7
所以盒子的个数是:30(个)
答:能做30个盒子.
【点评】本题考查了列一元一次方程解决实际问题的应用,解答时根据侧面个数与底面个数的比建立方程是解决本题的关键.
42.【答案】11,13;41,2n+1。
【分析】摆1个三角形要3根小棒,即2×1+1;
摆2个三角形要5根小棒,即2×2+1;
……
摆n个三角形需要的小棒数为:2n+1。
【解答】解:(1)2×5+1
=10+1
=11(根)
2×6+1
=12+1
=13(根)
(2)2×20+1
=40+1
=41(根)
摆n个三角形要用(2n+1)根小棒。
故答案为:11,13;41,2n+1。
【点评】本题主要考查数与形结合的规律,发现每多1个三角形就多2根小棒是解本题的关键。
43.【答案】(1)18人;(2)(2+4m)人;(3)10张。
【分析】一张餐桌可摆放2+4×1=6把椅子,可以坐6人;
两张餐桌可摆放2+4×2=10把椅子,可以坐10人;
三张餐桌可摆放2+4×3=14把椅子,可以坐14人;
所以n张餐桌可摆放2+4n把椅子,可以坐(2+4n)人;根据此解答即可。
【解答】解:(1)2+4×4=18(人)
答:四张餐桌可坐18人。
(2)按照这个规律摆放,m张餐桌可以坐(2+4m)人。
(3)2+4m=42,可得:m=10(张)
答:需要10张餐桌。
故答案为:(1)18人;(2)(2+4m)人;(3)10张。
【点评】本题考查了数与形结合的规律,关键是能根据求出的结果或观察图形得出规律。
44.【答案】见试题解答内容
【分析】(1)观察图形可得:第一幅图中有1个点;第二幅图中有1+2=3个点;第三幅图中有1+2+3=6个点,可以写成(32+3);第四幅图中有1+2+3+4=10个点,可以写成(42+4)由此可得第8个图形中的点数为:1+2+3+…+8(82+8)=36个点.
(2)结合(1)分析发现规律:第n个图形中有1+2+3+…+n(n2+n)个点.
【解答】解:(1)根据题干分析可得:
第8个图形中的点数为:
1+2+3+…+8
(82+8)
=36(个).
答:第8个图形中有36个点.
(2)结合(1)分析发现:
第n个图形中的点数为:1+2+3+…+n(n2+n)
答:第n个图形中有(n2+n)个点.
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力.解决此类问题的关键是:根据题干中的图形找出事物排列的一般规律.
45.【答案】见试题解答内容
【分析】由题意可知,最外层每边是54÷6=9(棵),每边不包括三角形顶点外9﹣2=7(棵),最外层一共载7×3+3=24(棵).第二层是边长为30米的等边三角形,用同样的方法即可求出一共有多少棵.再算出第三层、第四层(一共四层)棵数,进而计算出总棵数,用总棵数乘2就是小时姐姐共带的同学数.
【解答】解:如图
最外层:7×3+3=24(棵)
第二层:4×3+3=15(棵)
第三层:2×3+3=9(棵)
第四层:1棵
(24+15+9+1)×2
=49×2
=98(名)
答:小时姐姐共带了98名同学.
【点评】解答此题的关键,也是难点,是求出石榴树的总棵数.
46.【答案】见试题解答内容
【分析】根据题意得到摆1个三角形所需火柴棍的根数是3,2个三角形所需火柴棍的根数是5=3+2×1,3个三角形所需火柴棍的根数是7=3+2×2,…,于是得到摆15个三角形所需火柴棍的根数=3+2×14=31,进而可得摆n个三角形所需火柴棍的根数是3+2(n﹣1)=2n+1,n为正整数,据此解答.
【解答】解:(1)3+2×14
=3+28
=31(根);
(2)由分析可知:
摆n个三角形所需火柴棍的根数是(2n+1),n为正整数,
2n+1=79
2n=78
n=39
答:摆15个三角形需要31根小棒;用79根小棒可以摆39个三角形.
【点评】本题考查了数与形结合的规律,解决本题先由已知条件找到一般规律,再根据规律求解.
47.【答案】13,18,28,38;(5n+3),(10n+8)。
【分析】(1)根据所给图示发现,第一个图形正方形的个数为:5+3=8(个),周长为:10+8=18;第二个图形正方形的个数为:5×2+3=13(个),周长为:10×2+8=28;第三个图形正方形的个数为:5×3+3=18(个),周长为:10×3+8=38;据此完成填表。
(2)根据(1)中的数据总结规律,完成填空即可。
【解答】解:(1)第一个图形正方形的个数为:5+3=8(个),周长为:10+8=18;
第二个图形正方形的个数为:5×2+3=13(个),周长为:10×2+8=28;
第三个图形正方形的个数为:5×3+3=18(个),周长为:10×3+8=38;
填表如下:
图形 ① ② ③
正方形的个数 8 13 18
图形的周长 18 28 38
(2)推测第n个图形中,正方形的个数为(5n+3),周长为(10n+8)。
故答案为:13,18,28,38;(5n+3),(10n+8)。
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力。
48.【答案】我发现后面的算式会循环出现7641﹣1467=6174。
【分析】按要求任意写一个四位数,将这个四位数的四个数字重新组合,组成一个最大的数和一个最小的数,用大数减去小数,重复进行,找出规律。
【解答】解:根据题意举例解答。如1234。
4321﹣1234=3087
8730﹣3078=5652
6552﹣2556=3996
9963﹣3699=6264
6642﹣2466=4176
7641﹣1467=6174
7641﹣1467=6174
我发现后面的算式会循环出现7641﹣1467=6174。
【点评】本题主要考查数列中的规律,找到规律是解题的规律。
49.【答案】37.5厘米。
【分析】1个杯子的高度是15cm,把5个完全一样的杯子叠起来的高度是25cm,那么上面每个杯子露出(25﹣15)÷4=2.5(厘米),然后求出上面9个杯子露出的高度,再加上15厘米即可。
【解答】解:(25﹣15)÷4
=10÷4
=2.5(厘米)
2.5×(10﹣1)+15
=22.5+15
=37.5(厘米)
答:10个这样的杯子叠起来的高度是37.5厘米。
【点评】本题考查数和形中的找规律问题,找到共同特征解决问题即可。
50.【答案】见试题解答内容
【分析】根据图意,每一行从左到右,箭尾部的“∧”依次减少1个,且箭头的指向左右相反,进而选出答案即可.
【解答】解:根据图意,每一行从左到右,箭尾部的“∧”依次减少1个,且箭头的指向左右相反,
故选D.
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力.
51.【答案】见试题解答内容
【分析】观察题干可知,前面的两个图形中,上面数字之和等于第三个图形的上面数字;所以可得:右面的两个数字之和,也等于第三个图形中的右面数字,据此即可解答.
【解答】解:根据题干分析可得:12+12=24
16+10=26
故答案为:
【点评】主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.
52.【答案】(1)4000
(2)1000
【分析】(1)利用长方形面积公式:S=ab,计算人行道的面积,然后用人行道的面积除以每块地砖的面积,就是所需块数.
(2)根据图形的排列规律,每4×4=16(块)方砖中,有4块是红色的,求所需地砖块数包含几个16,再乘4,计算所需红色地砖的块数即可.
【解答】解:(1)400×1.6÷0.42
=640÷0.16
=4000(块)
答:铺设这条人行道一共需4000块地砖.
(2)4000÷16×4
=250×4
=1000(块)
答:铺设这条人行道一共需要1000块红色地砖.
【点评】本题主要考查数与形结合的规律,关键是根据图示发现地砖排列的规律.
53.【答案】这本书共有15页插图。
【分析】因为插图和文字按页排列为文、文、图、图、图、文、文、图、图、图、文……所以,可知显示出周期循环的特点,按照文、文、图、图、图5页一个循环。27中有5个循环,剩下的第26,27页分别是文、文。据此答题即可。
【解答】解:经分析得:
27÷5=5……2
5×3=15(页)
答:这本书共有15页插图。
【点评】本题考查简单周期问题。结合发现的规律,利用带余除法解决问题即可。
54.【答案】(1)(2x+4)人。
(2)34人。
(3)28张。
【分析】摆1张长方形桌子可以坐6个人,6=2×3,
摆2张长方形桌子可以坐8个人,8=2×4,
摆3张长方形桌子可以坐10个人,10=2×5,
……
摆x张长方形桌子可以坐的人数:2(x+2)=2x+4。
【解答】解:(1)x张桌子可以坐(2x+4)人。
(2)当x=15时,
2×15+4
=30+4
=34(人)
答:当x=15时,一共可以坐34人。
(3)2x+4=60
2x=56
x=28
答:摆28张桌子可以坐60人。
【点评】本题主要考查数与形结合的规律,发现每多1张桌子就多坐2人是解本题的关键。
55.【答案】20;32。
【分析】根据图示可知,摆一个独立的图形长方体需要4根小棒,第几个图形就摆几个长方形,据此利用乘法计算小棒的根数即可。
【解答】解:5×4=20(根)
8×4=32(根)
答:第5个图形有20根小棒;第8个图形有32根小棒。
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力。
56.【答案】3;BC;135平方厘米。
【分析】(1)通过观察统计图可知,点E从点A开始,3秒钟后到达点B。
(2)统计图中3秒到8秒表示点E在长方形边BC上移动。
(3)根据长方形的面积公式:S=ab,把数据代入公式解答。
【解答】解:(1)点E从点A开始,3秒钟后到达点B。
(2)统计图中3秒到8秒表示点E在长方形边BC上移动。
8﹣3=5(秒)
(3×5)×(3×3)
=15×9
=135(平方厘米)
答:长方形ABCD的面积是135平方厘米。
故答案为:3;BC。
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
57.【答案】见试题解答内容
【分析】(1)观察图形可知,第一个图形黑色三角形有1个,白色三角形1+2=3个;第二个图形黑色三角形有1+2=3个,白色三角形1+2+3=6个;第三个图形黑色三角形有1+2+3=6个,白色三角形1+2+3+4=10个;则第四个图形黑色三角形有1+2+3+4=10个,白色三角形1+2+3+4+5=15个;据此画图即可;
(2)由上述推算可得:第n个图形黑色三角形有1+2+3+…n个,据此即可解答问题.
【解答】解:(1)根据题干分析可得:
(2)第n个图形黑色三角形有1+2+3+…n个,
当n=10时
黑色三角形的个数是:55(个)
答:第10个图形中有 55块黑色的瓷砖.
故答案为:55.
【点评】主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.
58.【答案】20根。
【分析】求搭4个这样独立的五边形需要多少根小棒,就相当于求4个5是多少,用乘法计算。
【解答】解:5×4=20(根)
答:搭4个这样独立的五边形需要20根小棒。
【点评】本题解答依据是:求几个相同加数的和,用乘法计算。
六年级上册数学期中培优卷(人教版)
一.应用题(共58小题)
1.图中的涂色部分表示312.整个图形表示多少?
2.1、4、7、10、13、…这个数列中,有6个连续数字的和是159,那么这6个数中最小的是几?
3.如图,第二个图形是由第一个图形连接三边中点而得到的,第三个图形是由第二个图形中间的一个三角形连接三边中点而得到的,以此类推……分别写出第二个图形、第三个图形和第四个图形中的三角形个数.如果第n个图形中的三角形个数为8057,n是多少?
4.五(1)班进行团体操表演,排成下面的队形.如果再增加一些人,但是保持点阵的规律不变,至少增加多少人?
5.海豹是生活在海洋中的哺乳动物,它们一般靠肺呼吸,所以必须经常不断地浮到海面呼吸空气。一只海豹6时开始从海底经过9分钟慢慢浮到海面,然后浮出海面呼吸2分钟,最后再经过9分钟回到海底,这样有规律地进行这个过程。7时整海豹会在什么位置?(请你用喜欢的方式表示出你的思考过程和结果)
6.用小棒按照如图的方式摆图形.
(1)摆1个五边形需要 根小棒,摆2个五边形需要 根小棒,摆3个五边形需要 根小棒.
(2)照这样摆下去,
①摆5个五边形需要多少根小棒?摆10个呢?
②用61根小棒可以摆出多少个五边形?
7.按照下图方式摆放餐桌和椅子.
照这样摆下去,要坐34位客人需要多少张餐桌?(用方程解)
8.在计算一个数与15相乘时,有一种简便的算法﹣﹣“加半添0”法.例如,计算24×15,先用24的一半(即12)与24相加,得36;再在36的末尾添一个0,得360.你能用这种方法计算下面各题吗?
26×15
28×15
32×15
48×15
9.如图所示,用同样的小棒摆三角形。
①像这样摆下去,摆n个三角形,需要 根小棒。
②当n=100时,用第1题的式子计算摆100个三角形需要的小棒数。
10.一张桌子可以坐6人,两张桌子拼起来可以坐10人,三张桌子拼起来可以坐14人.像这样共几张桌子拼起来可以坐50人.
11.一张桌子可以坐6个人,两张桌子拼起来可以坐10个人,那么9张桌子像这样拼起来可以坐多少人?
12.按照如图方式摆图形.
(1)照这样,摆第15个图形需要用多少根小棒?
(2)如果摆出的图形用了21根小棒,那么摆到了第几个图形?
13.按如图中的方式摆放三角形积木,如果最下层放21块,那么共需放几层?
14.我们在初中的数学学习中将会经常用到后面的这个公式:a2﹣b2=(a+b)×(a﹣b),这个公式我们称为平方差公式,请你利用这个公式,解决下面这个数学问题。如图所示,边长分别为1、2、3、4、…、2013、2014的正方形叠放在一起,则图中阴影部分的面积是多少?
15.一个表面涂满了颜料的长方体小盒子平放在桌面上(如图1),它的长是5厘米,宽是4厘米,高是2厘米。现在将它沿着最长的棱翻转第一次(如图2位置),接又沿着最长的棱翻转第二次(如图3),然后又沿着最长的棱翻转第三次……,这样翻转后拿走小盒子,这时桌面上留下了颜料的印迹。
(1)如图2所示,翻转第一次后(不计算图1小盒子原来在桌面上的印迹)形成的印迹面积是 平方厘米。
(2)如果从第一次翻转形成印迹开始算起,到第4次翻转结束,留下的印迹总面积是 平方厘米。
(3)如果从第一次翻转形成印迹开始算起,到第2023次翻转结束,留下的印迹总面积是 平方厘米。
16.观察如图图形,第七个图形中,共有多少个三角形?
17.如图,数学实验室的窗户设计如图所示,如果每个符号代表一个数字,它们是837,571,206,439.求2018的图如何画?
18.某地举行庆丰收长桌宴,一张桌子坐6人,两张桌子并起来坐10人,三张桌子并起来坐14人……照这样并下去,参加宴会的共有402人,需要并多少张桌子?
19.小明和小军玩涂方格游戏,两人轮流涂小方格,每次只许涂相邻的1至5个小方格(两方格有公共边才算相邻),谁先没有方格再涂就算谁输.先涂的小明想:正方形是中心对称图形,只要先涂正中心的那一格,其余的每一格都能找到关于中心对称的另一格可涂,于是他先涂正中心的那一格,其余的每一格都能找到关于中心对称的另一格可涂,于是他先涂出了下面的例图.小明确保获胜,第一次还可以怎么涂,请把不同的涂法画出来(旋转后图案不同的算作不同的涂法,看你能涂出多少种)
20.仔细观察如图与算式的规律,并填空。
(1)(n+1)2﹣n2=
(2)利用发现的规律计算:102﹣92+82﹣72+62﹣52=
21.一种长方形餐桌的四周可坐6人用餐,现把若干张这样的餐桌按如图方式进行拼接.
(1)若把4张这样的餐桌拼接起来,四周分别可坐 人;若把8张这样的餐桌拼接起来,四周分别可坐 人.
(2)若用餐的人数有90人,则这样的餐桌需要多少张?
22.按照前两组的规律填数,你知道第三组的“?”处应该填几吗?
23.将图1边长为9厘米的等边三角形的每一个边长三等分,然后变化出图2所示的图形,求多边形的周长.
24.一张长方形桌子可坐6人,按下列方式将桌子拼在一起.
(1)2张桌子拼在一起可坐多少人?3张桌子拼在一起可坐多少人?
(2)一家餐厅有40张这样的长方形桌子,按照如图方式每5张桌子拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐多少人?
(3)若在(2)中,改成每8张桌子拼成1张大桌子,则共可坐多少人?
25.斐波那契数列由十三世纪意大利数学家斐波那契发现.数列中的一系列数字常常被人们称之为神奇数、奇异数.具体数列为1,1,2,3,5,8,13,21,34,…
26.一张桌子坐4人,两张桌子并起来坐6人,三张桌子并起来坐8人,…照这样计算,10张桌子并成一排可坐多少人?如果一共有26人,需要并多少张桌子?
27.把5张图画像如图这样钉在墙上,一共要用多少个图钉?
28.(如图所示)用小棒按下图摆六边形:摆1个六边形需要5+1=6根小棒,摆2个六边形需要2×5+1=11根小棒,摆3个六边形需要3×5+1=16根小棒,…
①像这样摆下去,摆m个六边形一共需要多少根小棒?(请用含有字母m的式子表示)
②当m=10时,用第①题的式子计算摆10个六边形一共需要多少根小棒?
29.用绿、白两种颜色的小方块瓷砖400块贴成一正方向墙面,这个墙面最外层铺的是白色瓷砖.由外到内的第二层是绿色瓷砖,第三层是白色瓷砖,第四层又是绿色…,那么,这个墙面上绿色瓷砖共有多少块?
30.小华把一些珠子放在桌子上的15个盒子中,已知盒子中的珠子数按盒子从左往右的顺序成一个等差数列,任一盒子中不止两颗珠子,并且从左数第8个盒子中有24颗珠子.请问:这15个盒子中一共有多少颗珠子?
31.如图里的数和它周围3个里的数有关系。想一想,里应当填什么数?应当填 。
用算式表示你的想法:
因为: 、
所以:
32.杨辉三角,是中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现的一种几何排列.你能计算图中的杨辉三角中一共有多少个数字吗?
33.用一根长96cm的绳子在地上摆正方形.当这根绳子摆出48个正方形时,正方形的边长是多少厘米?顶点有几个?
34.快乐提升:
如图,摆一个三角形用3根小棒,增加2根,可以摆出一个平行四边形,继续增加2根,摆出一个梯形,照这样摆下去,21根小棒能摆出一个什么样的图形?51根呢?
35.某饭店的餐桌都是能坐4人的正方形,当团体客人在10人以上时,饭店允许客人将餐桌拼成一长条,但每张桌子不能有空位,问如果团体客人是22人,那么需要几张桌子?
36.先观察前三题计算结果,再直接写出最后两题的得数。
0.1+0.11=0.21
0.1+0.11+0.111=0.321
0.1+0.11+0.111+0.1111=0.4321
0.1+0.11+0.111+0.1111+…+0.1111111=
0.1+0.11+0.111+0.1111+…+0.111111111=
37.用小棒按下面的方式拼图形.
(1)如果按下面的规律拼成5个这样的五边形,一共要用 根小棒.
五边形
个数 拼成的形状 小棒根数
1 5
2 9
3 13
4 17
(2)接着拼下去,一共用了57根小棒,你知道一共拼成了多少个五边形吗?
38.一串数:,,,,,,,,,,……
(1)第800个数是多少?
(2)是第几个数?
(3)前552个数的和是多少?
(4)前n个数的和能否等于106,如果能,试求出n的值,如果不能,试说明理由.
39.用6根同样长的小棒可以摆成一个正六边形(如图①),再接着摆下去(如图②、③、④),图⑧一共需要多少根小棒?
40.笑笑用水果卡片摆成下面的“T”字,照这样摆下去,第10个“T”字要用多少张水果卡片?
41.用正方形硬纸板做三棱柱盒子,每个盒子由3个举行侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面;B方法:剪4个侧面和5个底面
现有19章硬纸板,裁剪时x张用A方法,其余用B方法
(1)用x的代数式分别表示出裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做出多少个盒子?
42.用小棒摆三角形如图:
摆1个三角形要用3根小棒,摆2个三角形要用5根小棒,摆3个三角形要用7根小棒,摆4个三角形要用9根小棒。
(1)照这样,摆5个三角形要用 根小棒,摆6个三角形要用 根小棒。
(2)照这样摆下去,摆20个三角形要用 根小棒。摆n个三角形要用 根小棒.(用含有n的算式表示)
43.如图摆放餐桌和椅子:
(1)一张餐桌可坐6人,两张餐桌可以坐10人,四张餐桌可坐多少人?
(2)按照这个规律摆放,m张餐桌可以坐多少人?
(3)按照这个规律摆放餐桌,要坐42人,需要多少张餐桌?
44.观察点阵图形,找出规律.
(1)第8个图形中有多少个点?
(2)第n个图形中有多少个点?
45.10月1日小时姐姐带领大家去旅游,来到一块形状是等边三角形的果园,它的边长是54米,三边及内部都植满了石榴树;每棵树之间均相距6米,各个顶点上都植有一棵;小时姐姐给同学们分工,每两位同学栽一棵,正好分完.聪明的你知道小时姐姐共带了多少名同学吗?
46.已知摆1个三角形需要3根小棒,摆2个三角形需要5根小棒,摆3个三角形需要7根……按照这样的规律,摆15个三角形需要多少根小棒?用79根小棒可以摆多少个三角形?
47.如图是由边长为1的正方形按照某种规律排列而成的。
(1)观察图形,填写下表。
图形 ① ② ③
正方形的个数 8 18
图形的周长
(2)推测第n个图形中,正方形的个数为 ,周长为 。
48.任意写一个四位数(各个数位上的数字互不相同),将这个四位数的四个数字重新组合,求出其中最大的数与最小的数的差,再将得到的差像上面那样重新组合,重复这个过程,你发现了什么?
49.如图,1个杯子的高度是15cm,把5个完全一样的杯子叠起来的高度是25cm,那么10个这样的杯子叠起来的高度是多少厘米?
50.观察下图中图形的规律,图形?应该是
A.B.C.D.E.F.
51.找规律在空格或括号里填上适当的数.
52.海安某步行街要铺设一条人行道,人行道长400米,宽1.6米.现在用边长都是0.4米的红、黄两种正方形地砖铺设(如图是铺设的局部图示).
(1)请帮忙算一算,铺设这条人行道一共需多少块地砖?(不计损耗)
(2)铺设这条人行道一共需要多少块红色地砖?(不计损耗)
53.有一本漫画书共27页,插图和文字按页排列为文、文、图、图、图、文、文、图、图、图、文……照这样计算,这本书共有多少页插图?
54.一张长方形桌子可以坐6个人,按照下图的方式摆放桌椅。
(1)像这样摆下去,x张桌子可以坐多少人?
(2)当x=15时,一共可以坐多少人?
(3)像这样,摆多少张桌子可以坐60人?
55.佳佳摆小棒(如图),照这样摆下去,第5个图形有多少根小棒?第8个呢?
56.如图1,在长方形ABCD中,点E从点A开始,以每秒3厘米的速度沿长方形的边AB、BC、CD匀速移动。随着点E的移动,三角形ADE的面积会不断发生变化。它的面积变化情况如图2所示。
(1)点E从点A开始移动, 秒后到达点B。
(2)图2中3秒到8秒表示点E在长方形的边 上移动。
(3)长方形ABCD的面积是多少?
57.如图是由同型号黑白两种颜色的三角形瓷砖按一定规律铺设的图形.
(1)请在虚线框内画出第4个图形.(只要画出示意图)
(2)第10个图形中有 块黑色的瓷砖.
58.一个五边形需要5根小棒,那么搭4个五边形,需要几根小棒?
数学广角-数与形应用题(提高)
六年级上册数学期中培优卷(人教版)
参考答案与试题解析
一.应用题(共58小题)
1.【答案】见试题解答内容
【分析】在这里是把一个正方形的面积看作单位“1”,把它平均分成8份,每份是它的,其中1份涂色,表示,即这个正方形的表示312,根据分数除法的意义,用312除以8就是整个图形表示的数,或根据整数乘法的意义,用312乘8就是或个图形所表示的数.
【解答】解:3122496
或312×8=2496
答:整个图形表示2496.
【点评】解答此题的关键是明白涂色部分占整个图形的.
2.【答案】见试题解答内容
【分析】据题意可知,这个数列是公差为3的等差数列,由此可设这6个数中最小的数为x,则后边5个数与第一个数的差分别为3,6,…15,又因为有6个连续数的和是159,据此可得等量关系式:x+(x+3)+…+(x+15)=159,解此方程即得这6个数中最小的是多少.
【解答】解:设这6个数中最小的数为x,据题意可得方程:
x+(x+3)+…+(x+15)=159
6x+(3+6+…+15)=159
6x+45=159
6x=114
x=19
答:这6个数中最小的是19.
【点评】根据数列的排列规律及已知条件列出等量关系式是完成本题的关键.
3.【答案】见试题解答内容
【分析】根据图示,发现其规律为:第一个图形中三角形个数:1个;第二个图形中三角形个数:1×4+1=5(个);第三个图形中三角形个数:2×4+1=9(个);第四个图形中三角形个数:3×4+1=13(个);第n个图形中三角形个数:(n﹣1)×4+1=(4n﹣3)(个),计算n的值即可.
【解答】解:第一个图形中三角形个数:1个;
第二个图形中三角形个数:1×4+1=5(个);
第三个图形中三角形个数:2×4+1=9(个);
第四个图形中三角形个数:3×4+1=13(个);
第n个图形中三角形个数:
(n﹣1)×4+1=(4n﹣3)(个)
4n﹣3=8057,n=2015.
答:n是第2015个图形.
【点评】本题主要考查数与形结合的规律,关键根据所给图示发现图示排列的规律,并运用规律做题.
4.【答案】见试题解答内容
【分析】观察图形可知,这个点阵是个正方形的,每天边上都是3人,若再增加一些人,但是保持点阵的规律不变,则每条边上至少是4人,由此时人数减去原来的人数即可解答问题.
【解答】解:根据题干分析可得:4×4﹣3×3
=16﹣9
=7(人)
答:至少增加7人.
【点评】主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.
5.【答案】海底。
【分析】根据题意,6时到7时是1小时,为60分钟;海豹完成一次从海底到海面再回到海底的过程是需要9+2+9=20(分钟),据此计算解答即可。
【解答】解:6时到7时是1小时,为60分钟;
海豹完成一次从海底到海面再回到海底的过程是需要9+2+9=20(分钟);
60÷20=3(次),
即60分钟的时间,海豹正好可以完成3次海底到海面再回到海底的过程;7时整,海豹刚好回到海底。
故答案为:海底。
【点评】本题考查规律探究问题,根据整个过程所用时间计算即可。
6.【答案】见试题解答内容
【分析】(1)根据图示可知,摆一个五边形需要5根小棒,摆2个五边形需要9根小棒,也可以写成5+4×1=9(根)小棒,摆3个五边形需要13根小棒,也可以写成5+4×2=13(根)小棒…以后每增加一个五边形,需要的小棒个数就会增加4根,由此可得摆n个五边形需要5+4(n﹣1)=4n+1根小棒.
(2)①根据(1)中推理的推论,摆5个五边形需要4×5+1=21根小棒,摆10个五边形需要4×10+1=41根小棒.
②根据(1)中的推理的推论,设4n+1=61,可求出n的值既是所需摆出的五边形的个数.
【解答】解:(1)根据图示可知,摆1个五边形需要5根小棒,摆2个五边形需要5+4×1=9(根)小棒,
摆3个五边形需要5+4×2=13(根)小棒.
(2)①根据(1)中推理可得:摆n个五边形需要5+4(n﹣1)=4n+1根小棒,
摆5个五边形为:4×5+1=21(根),则摆5个五边形需要21根小棒;
摆10个五边形为:4×10+1=41(根),则摆10个五边形需要41根小棒.
②当4n+1=61时,可得4n=60,最终解得:n=15,所以用61根小棒可以摆出15个五边形.
故答案为:5,9,13.
【点评】本题考查了图形变化类,解决本题的关键是观察图形找到规律,并最终进行求解.
7.【答案】见试题解答内容
【分析】观察摆放的桌子,不难发现:在1张桌子坐6人的基础上,多1张桌子,多4人;设有n张桌子:
n=1时,可坐6人,可以写成4×1+2;
n=2时,可坐10人,可以写成4×2+2;
n=3时,可坐14人,可以写成4×3+2;
…;
所以n张桌子可坐(4n+2)人.
由此规律可得方程:4n+2=34;然后列方程解答即可.
【解答】解:设有n张桌子,
4n+2=34
4n=32
n=8
答:要坐34位客人需要8张餐桌.
【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,设未知数为n,由此列方程解决问题.
8.【答案】见试题解答内容
【分析】根据巧算的方法:“加半添0”法解答即可.
【解答】解:26÷2+26=39
所以26×15=390
28÷2+28=42
所以28×15=420
32÷2+32=48
所以32×15=480
48÷2+48=72
所以48×15=720
【点评】解答此题的关键是找出算式之间数与数的关系,得出规律,再根据规律解决问题.
9.【答案】①2n+1;②201根。
【分析】①由图可以看出摆一个三角形用3根小棒,摆两个三角形用5根小棒,摆三个三角形用7根小棒,摆四个三角形用9根小棒……,所以摆n个三角形用(2n+1)根小棒。
②把n=100代入2n+1,即可求出摆100个三角形需要的小棒数。
【解答】解:①一个三角用2×1+1=3(根)
二个三角形用2×2+1=5(根)
三个三角形用2×3+1=7(根)
四个三角形用2×4+1=9(根)
……
n个三角形用(2n+1)根
答:摆n个三角形需(2n+1)根小棒
②当n=100时
2n+1
=2×100+1
=200+1
=201(根)
答:摆100个三角形需要201根小棒。
故答案为:2n+1。
【点评】此题主要是初步渗透不完全归纳思想和代数思想,培养符号化意识,提高抽象和概括能力,关键是找规律,找到规律,代入数值计算比较简单。
10.【答案】见试题解答内容
【分析】由一张桌子坐6人,两张桌子坐10人,三张桌子坐14人,可以发现每多一张桌子多4个人,由此用字母表示这一规律,然后代值计算.
【解答】解:1张桌子可坐2×1+4=6人,
2张桌子拼在一起可坐2×4+2=10人,
3张桌子拼在一起可坐4×3+2=14人,
…
所以五张桌子坐4×5+2=22人,
…
那么n张桌子坐(4n+2)人.
当共有50人时,
4n+2=50
4n=48
n=12
答:这样共12张桌子拼起来可以坐50人.
【点评】此题考查图形的变化规律,找出规律,利用规律解决问题.
11.【答案】38。
【分析】由一张桌子坐6人,两张桌子坐10人,三张桌子坐14人,可以发现每多一张桌子多4个人,由此用字母表示这一规律,然后代值计算。
【解答】解:1张桌子可坐2×1+4=6(人)
2张桌子拼在一起可坐2×4+2=10(人)
3张桌子拼在一起可坐4×3+2=14(人)
…
所以五张桌子坐4×5+2=22(人)
…
那么n张桌子坐(4n+2)人
当n=9时,
4×9+2
=36+2
=38(人)
答:这样共9张桌子拼起来可以坐38人。
【点评】此题考查图形的变化规律,找出规律,利用规律解决问题。
12.【答案】见试题解答内容
【分析】(1)摆1个三角形所需小棒的根数=3,2个三角形所需小棒的根数=3+2,3个三角形所需小棒的根数=3+2×2,…,于是得到n个三角形所需小棒的根数=3+2×(n﹣1)=2n+1,然后把n=15代入计算即可;
(2)根据上面得出的规律,可得如果摆出的图形用了21根小棒,即2n+1=21,据此求出n的值即可解答问题.
【解答】解:(1)1个三角形所需小棒的根数=3
2个三角形所需小棒的根数=3+2
3个三角形所需小棒的根数=3+2×2
…
所以n个三角形所需小棒的根数=3+2×(n﹣1)=2n+1
当n=15时,2n+1=2×15+1=31(根)
答:像这样摆下去第15个图摆了31个三角形.
(2)总根数=21时
2n+1=21
2n=22
n=11
答:如果用了21根小棒,他摆了18个三角形.
【点评】本题考查了规律型:图形的变化类,通过从一些特殊的图形变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.
13.【答案】11.
【分析】根据图示可知:1层最下层有1块;2层最下层有3块;3层最下层有5块;……最下层有21块,层数为:(21+1)÷2=11(层)。据此解答。
【解答】解:根据分析,最下层放21块,层数为:
(21+1)÷2
=22÷2
=11(层)
答:一共需要放11层.
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力.
14.【答案】2029105。
【分析】根据所给图示可知,该阴影部分的面积为:(20142﹣20132)+(20122﹣20112)+……+(42﹣32)+(22﹣12)。利用平方差公式计算即可。
【解答】解:(20142﹣20132)+(20122﹣20112)+……+(42﹣32)+(22﹣12)
=(2014+2013)(2014﹣2013)+(2012+2011)(2012﹣2011)+……+(4+3)(4﹣3)+(2+1)(2﹣1)
=2014+2013+2012+2011+……+4+3+2+1
=1007×2015
=2029105
答:阴影部分的面积是2029105。
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和应用公式解决问题的能力。
15.【答案】10,100,30340。
【分析】由题干中的长方体可知,上下两个面大小相等,左右两个侧面相等,前后两个面相等。第一层1次翻转后右侧面向下,第2次翻转后上面向下,第3次翻转后左侧面向下,第4次翻转后下面向下……据此分析解答。
【解答】解:(1)5×2=10(平方厘米)
如图2所示,翻转第一次后(不计算图1小盒子原来在桌面上的印迹)形成的印迹面积是10平方厘米。
(2)4÷2=2(个)
(4×5+2×5)×2
=30×2
=60(平方厘米)
答:如果从第一次翻转形成印迹开始算起,到第4次翻转结束,留下的印迹总面积是60平方厘米。
(3)2023÷4=505(个)……3(次)
60×505+4×5+5×2×2
=30300+20+20
=30340(平方厘米)
答:如果从第一次翻转形成印迹开始算起,到第2023次翻转结束,留下的印迹总面积是30350平方厘米。
故答案为:10,100,30340。
【点评】解决本题的关键是理解每次翻转后那个面向下,结合长方形的面积公式,分析解答即可。
16.【答案】见试题解答内容
【分析】根据图示,发现这组图形的规律:第一个图形三角形个数:4个,第二个图形三角形个数:4×2=8(个);第三个图形三角形个数:4×3=12(个);……第n个图形三角形的个数:4n个.据此解题.
【解答】解:第一个图形三角形个数:4个
第二个图形三角形个数:4×2=8(个)
第三个图形三角形个数:4×3=12(个)
……
第n个图形三角形的个数:4n个
所以第七个图形三角形的个数:
4×7=28(个)
答:第七个图形三角形共有28个.
【点评】本题主要考查数与形结合的规律,关键根据所给图形,发现其规律,并运用规律做题.
17.【答案】见试题解答内容
【分析】观察图案和数据可知:837,439第2位都是3,观察图形可知,只有第2行和第4行是这两个数,第2行和第4行的末尾数字图形是7或者9,而571是其中一个数,第1行和第3行只有第一行的第2个图形是前面的那个7或9,所以第1行的数字是571,第2行是439,第3行是206,第4行是837,据此即可得出代表1995的符号.
【解答】解:由图案和提供的数据可知:837,439第2位都是3,所以只有第2行和第4行是这两个数,第2行和第4行的末尾数字图形是7或者9,而571是其中一个数,第1行和第3行只有第一行的第2个图形是前面的那个7或9,所以第1行的数字是571,第2行是439,第3行是206,第4行是837;
即0,1,2,3,4,5,6,7,8,9分别用符号:
2018是:
【点评】本题考查了用符号(窗户形状)代表阿拉伯数码,解题的关键是由相同的数字得出对应的图案,找到突破口.
18.【答案】100张。
【分析】根据题意发现:一张桌子坐6人,每多1张桌子就多坐4人,则拼n张桌子,能坐(4n+2)个人;据此逆推即可。
【解答】解:(402﹣2)÷4
=400÷4
=100(张)
答:需要并100张桌子。
【点评】本题考查了图形的变化类题目,认真观察、分析和归纳总结是解决此题的关键。
19.【答案】见试题解答内容
【分析】整个图形是中心对称图形,先涂的仍旧涂出一个以正方形中心为对称点的中心对称图形,接下来,无论小军怎么涂,小明都可以在对称的位置上涂,确保获胜.
【解答】解:小明仍旧涂出一个以正方形中心为对称点的中心对称图形即可,如图:
【点评】本题主要考查了学生灵活解决生活中实际问题的能力,本题以正方形中心为对称点是解题关键.
20.【答案】2n+1;45。
【分析】根据仔细观察如图与算式的规律,可知(n+1)2﹣n2=2n+1;利用发现的规律,102﹣92+82﹣72+62﹣52=(102﹣92)+(82﹣72)+(62﹣52),然后结合规律解答即可。
【解答】解:(1)(n+1)2﹣n2=2n+1。
(2)利用发现的规律计算:
102﹣92+82﹣72+62﹣52
=(102﹣92)+(82﹣72)+(62﹣52)
=10+9+8+7+6+5
=45
答:(1)(n+1)2﹣n2=2n+1。
(2)利用发现的规律计算:102﹣92+82﹣72+62﹣52=45。
故答案为:2n+1;45。
【点评】本题考查了算式的规律,首先仔细观察如图与算式,找出规律,然后结合题意分析解答即可。
21.【答案】见试题解答内容
【分析】观察图形发现:一种长方形餐桌的四周可坐6人用餐,多一个长方形餐桌,多用4个人,则第n张餐桌,需要可坐(2+4n)人.
【解答】解:根据分析可得,
第n张餐桌,需要可坐(2+4n)人.
(1)2+4×4=18(人)
2+4×8=34(人)
答:若把4张这样的餐桌拼接起来,四周分别可坐 18人.若把8张这样的餐桌拼接起来,四周分别可坐34人.
(2)2+4n=90
4n=88
n=22
答:若用餐的人数有90人,则这样的餐桌需要22张.
故答案为:18,34.
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力.
22.【答案】
【分析】左下角、右下角以及中间这三个数的和等于最上面那个数,据此求解即可。
【解答】解:35+18+30
=53+30
=83
【点评】解答此题的关键是,根据所给出的数列的数的特点,找出规律,再根据规律解决问题。
23.【答案】见试题解答内容
【分析】根据周长的意义,围成图形一周的长度叫做周长;在此题中等边三角形的边长为9厘米,变化出图2所示的图形的边长可求为3厘米,共12条边,用一条边的长度乘以12即可求解.
【解答】解:9÷3=3(厘米)
3×12=36(厘米)
答:多边形的周长是36厘米.
【点评】本题主要考查了周长的意义,即围成图形一周的长度叫做周长.
24.【答案】(1)8,10;(2)112;(3)100.
【分析】(1)根据图示2张桌子拼一起,可以坐:6+2=8(人),3张桌子拼一起,可以坐:6+2+2=10(人).
(2)先根据(1)的规律,计算5张桌子拼一起,可以坐的人数:6+2+2+2+2=14(人),再计算40张桌子可以拼成几个大桌子,然后乘14,计算可坐人数.
(3)根据规律计算8张桌子拼一起,可以坐的人数:6+2+2+2+……+2=6+2×(8﹣1)=20(人),然后计算40张桌子可以拼成几个大桌子,乘20就是一共可坐的人数.
【解答】解:(1)6+2=8(人)
6+2+2=10(人)
答:2张桌子拼在一起可坐8人;3张桌子拼在一起可坐10人.
(2)6+2+2+2+2=14(人)
8×14=112(人)
答:共可坐112人.
(3)6+2+2+2+2+2+2+2
=6+2×(8﹣1)
=6+14
=20(人)
40÷8×20
5×20
=100(人)
答:改成每8张桌子拼成1张大桌子,则共可坐100人.
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力.
25.【答案】见试题解答内容
【分析】观察数列的奇偶性发现:第1、2个数是奇数,第3个数是偶数;第4、5个数是奇数,第6个数是偶数……,每三个数看成一组,每组的前两个数是奇数,第三个数是偶数,用100除以3,求出商和余数,再根据余数进行判断,由此求解.
【解答】解:100÷3=33……1
余数是1,所以第100个数是第34个循环的第1个数,是奇数.
答:第100个数是奇数.
【点评】解决这类问题关键是把重复出现的部分看成一组,根据除法的意义,求出总数量里面有多少个这样的一组,还余几,然后根据余数进行推算.
26.【答案】见试题解答内容
【分析】观察摆放的桌子,不难发现:在1张桌子坐4人的基础上,多1张桌子,多2人.由此规律即可解决问题.
【解答】解:(1)n=1时,可坐4人,可以写成2×1+2
n=2时,可坐6人,可以写成2×2+2
n=3时,可坐8人,可以写成2×3=2
…
所以当n=10时,可坐2×10+2=22人
答:10张桌子并成一排可坐22人.
(2)2n+2=26
2n=24
n=12
答:如果有26人,需要12张桌子.
【点评】主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.
27.【答案】18。
【分析】由图可知,所需要的图钉为上、中、下3排,每排6个,每排的个数乘排数即为要用的图钉总数,据此解答。
【解答】解:6×3=18(个)
答:一共要用18个图钉。
【点评】本题考查了学生对于图形的观察能力,由图读出相关信息是解决此题的关键。
28.【答案】①(5m+1)根;
②51根。
【分析】①摆1个六边形需要5+1=6根小棒,摆2个六边形需要2×5+1=11根小棒,摆3个六边形需要3×5+1=16根小棒,……,摆m个六边形需要小棒:(5m+1)根。
②把m=10时,代入①中的公式,计算即可。
【解答】解:①摆1个六边形需要5+1=6根小棒
摆2个六边形需要2×5+1=11根小棒
摆3个六边形需要3×5+1=16根小棒
……
摆m个六边形需要小棒:(5m+1)根
答:摆m个六边形一共需要(5m+1)根小棒。
②当m=10时,
5×10+1
=50+1
=51(根)
答:摆10个六边形一共需要51根小棒。
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力。
29.【答案】见试题解答内容
【分析】因为正方形墙共用100块小方砖网贴成,设每块小方砖为1个面积单位,则正方形墙的面积为100个面积单位,边长为20个长度单位,每块小方砖的边长为1个长度单位.由题意可知,由外到内,最外层(白方砖)的边长为20个长度单位,第二层(绿方砖)边长为18个长度单位,第三层(白方砖)边长为16个长度单位,第四层(绿方砖)边长为14个长度单位……由此可知,由外到里,绿色方砖的边长分别为18、14、10、6、2.由此即可计算出绿方砖的块数.
【解答】解:由外到内绿方砖是第二层、第四层、第站层……(偶数层)
第二层边长为18个长度单位,方砖块数为:18×2+(18﹣2)×2=36+32=68(块)
第四屋边长为14个长度单位,方砖块数为14×2+(14﹣2)×2=28+24=52(块)
第六层边长为10个长度单位,方砖块数为10×2+(10﹣2)×2=20+16=36(块)
第八层边长为6个长度单位,方砖块数为6×2+(6﹣2)×2=12+8=20(块)
第十层(也是最内层)边长是2个长度单位,方砖块数为2×2+(2﹣2)×2=4+0=4(块)
68+52+36+20+4=180(块)
答:这个墙面上绿色瓷砖共有180块.
【点评】此题可通过画图找出每层绿色方砖与层数之间的关系,求出每层绿色方砖的块数,进而求出一共用绿色方砖的块数.
30.【答案】见试题解答内容
【分析】15个盒子中的珠子从左到右是一个项数为15的等差数列,其中第8个盒子中的珠子数为中间项,根据等差数列的意义,与中间项相邻的左、右两项之和等于中间项,与中间项相隔1项的左、右两项之和也等于中间项……因此,这15项之和就是等于中间项乘中间项数.
【解答】解:24×15=360(颗)
答:这15个盒子中一共有360颗珠子.
【点评】解答此题的关键是明白:与中间项相邻的左、右两项之和等于中间项,与中间项相隔1项的左、右两项之和也等于中间项……
31.【答案】3,里的数等于它周围3个的数的和,10=6+1+3,=3。
【分析】根据图示发现:里的数等于它周围3个里的数的和。据此解答。
【解答】解:因为:里的数等于它周围3个的数的和、10=6+1+3
所以:=3
故答案为:3,里的数等于它周围3个的数的和,10=6+1+3,=3。
【点评】通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力。
32.【答案】见试题解答内容
【分析】经过观察发现,这些数字组成的三角形是等腰三角形,两腰上的数都是1,第1行有1个数字,第2行有2个数字,第,3行有3个数字,…,一共10行,有1+2+3+4+5+6+7+8+9+10=55(个)数字,据此解答即可.
【解答】解:根据分析可知:
1+2+3+4+5+6+7+8+9+10=55(个)
答:图中的杨辉三角中一共有55个数字.
【点评】本题考查了数与形结合的变化规律,主要培养学生的观察能力和总结能力.
33.【答案】见试题解答内容
【分析】根据图示,发现这组图形的规律:第一个图形:正方形个数:1个,顶点个数:4个,边长:96÷4=24(厘米);第二个图形:正方形个数:2个,顶点个数:4+3=7(个),边长:96÷(4×2)=12(厘米);第三个图形,正方形个数:3个,顶点个数:4+3+3=10(个),边长:96÷(4×3)=8(厘米);……第n个图形正方形个数:n个,顶点个数:4+3(n﹣1)=(3n+1)个,边长:(96÷4n)厘米.据此解答.
【解答】解:第一个图形:正方形个数:1个,顶点个数:4个,边长:96÷4=24(厘米)
第二个图形:正方形个数:2个,顶点个数:4+3=7(个),边长:96÷(4×2)=12(厘米)
第三个图形,正方形个数:3个,顶点个数:4+3+3=10(个),边长:96÷(4×3)=8(厘米)
……
第n个图形正方形个数:n个,顶点个数:4+3(n﹣1)=(3n+1)个,边长:(96÷4n)厘米
由规律可知:
第48个图形的正方形个数为48个,
顶点个数为:
3×48+1
=144+1
=145(个)
边长:
96÷(4×48)
=96÷192
=0.5(厘米)
答:这根绳子摆出48个正方形时,正方形的边长是0.5厘米,顶点有145个.
【点评】本题主要考查数与形结合的规律,关键根据所给图形,发现其规律,并运用规律做题.
34.【答案】见试题解答内容
【分析】根据图示可知:摆1个三角形需要小棒:3根;摆2个三角形需要小棒:3+2=5(根);摆3个三角形需要小棒:3+2+2=7(根);……摆n个三角形需要小棒:3+2(n﹣1)=(2n﹣1)根.根据规律计算21、51根小棒可以摆几个三角形,进而判断其形状.
【解答】解:摆1个三角形需要小棒:3根
摆2个三角形需要小棒:3+2=5(根)
摆3个三角形需要小棒:3+2+2=7(根)
……
摆n个三角形需要小棒:3+2(n﹣1)=(2n﹣1)根
由图形可以知道:奇数个(1除外)三角形可以摆成梯形,偶数个三角形可以摆成平行四边形.
21根小棒摆三角形的个数:
2n﹣1=21
2n=22
n=11
11为奇数
51根小棒摆成三角形的个数:
2m﹣1=51
2m=52
m=26
26为偶数
答:21根小棒可以摆成梯形;51根小棒可以摆成平行四边形.
【点评】本题主要考查数与形结合的规律,关键根据图示发现其规律,并运用规律做题.
35.【答案】见试题解答内容
【分析】把餐桌拼成长条,如图:
1张桌子可坐:4人
2张桌子可坐:4+2=6(人)
3张桌子可坐:4+2+2=8(人)
……n张桌子可坐:
4+2(n﹣1)=(2n+2)人
由此求出当有22人时需要的桌子数量即可.
【解答】解:1张桌子可坐:4人
2张桌子可坐:4+2=6(人)
3张桌子可坐:4+2+2=8(人)
……n张桌子可坐:
4+2(n﹣1)=2n+2(人)
2n+2=22
2n+2﹣2=22﹣2
2n=20
n=10
答:需要10张桌子.
【点评】本题先画出图,结合图找出规律,再利用规律求解.
36.【答案】0.7654321;0.987654321。
【分析】通过观察:0.1+0.11=0.21
0.1+0.11+0.111=0.321
0.1+0.11+0.111+0.1111=0.4321
得出规律:得数看最后一个加数,如果最后一个加数的小数点后的有n(n≤9)个1,
得数的小数点后的数就从n依次从大到小排列到1,据此解答即可。
【解答】解:0.1+0.11=0.21
0.1+0.11+0.111=0.321
0.1+0.11+0.111+0.1111=0.4321
0.1+0.11+0.111+0.1111+…+0.1111111=0.7654321
0.1+0.11+0.111+0.1111+…+0.111111111=0.987654321
故答案为:0.7654321;0.987654321。
【点评】解决本题的关键是找出规律:得数看最后一个加数,如果最后一个加数的小数点后的有n(n≤9)个1,得数的小数点后的数就从n依次从大到小排列到1。
37.【答案】见试题解答内容
【分析】(1)由图示可知,拼1个五边形,需要小棒根数:5根;拼2个五边形,需要小棒根数:5+4=9(根);拼3个五边形,需要小棒根数:5+4+4=13(根);……有摆n个五边形,需要小棒根数:5+4×(n﹣1)=(4n+1)(根).根据规律计算即可.
(2)由(1)的规律可知,当4n+1=57时,n=14.
【解答】(1)拼1个五边形,需要小棒根数:5根
拼2个五边形,需要小棒根数:5+4=9(根)
拼3个五边形,需要小棒根数:5+4+4=13(根)
……
有拼n个五边形,需要小棒根数:5+4×(n﹣1)=(4n+1)(根)
当n=5时,所需小棒根数:
4×5+1
=20+1
=21(根)
答:拼成5个这样的五边形,一共要用 21根小棒.
(2)解:设一共拼成了x个五边形.
4x+1=57
4x=56
x=14
答:一共拼成了14个五边形.
故答案为:21.
【点评】本题主要考查数与形结合的规律,关键根据所给图示发现图示排列的规律,并运用规律做题.
38.【答案】(1);(2)第261个数或第285个数;(3)287.5;(4)存在前n个数的和等于106,此时n的值是201。
【分析】观察数列,,,,,,,,,,……,可发现:分母为1的分数有1个,分母为2的数有3个,分母为3的数有5个,所以可得出:分母为n的分数有2n﹣1个;分子都是从1开始到与分母的数字相同连续的自然数,再倒数回到1,由此规律解决问题:
(1)首先要计算第800个数之前最大的平方是:当n=28时,n2=784,第784个数是分母为28的最后一个数,所以可以找到第800个数;
(2)先找出分母是16的最后一个数,是第162个数,162=256,再向右数5个即可,因为同一个分母的数除中间为1的数是出现一次外,其余都是出现2次,所以倒数第5个数也是,得出结论;
(3)同(1)同理,先计算第552个数之前最大的平方数:当n=23时,n2=529,先计算分母为1至23的所有分数之和:1+2+3+……+23的值,再确定第529到552之间数的和,最后相加即可;
(4)因为分母为n的分数有2n﹣1个,且这2n﹣1个分数相加和为n;所以分母为n时,前n2个数的和为,确定当n为最大时,最接近106时的n=14,即前196个数的和为105,与106还相差1,分母为15的分数能否达到几个分数和为1,来判断。
【解答】解:观察数列,,,,,,,,,,……,可发现:分母为1的分数有1个,分母为2的数有3个,分母为3的数有5个,所以可得出:分母为n的分数有2n﹣1个;且这2n﹣1个分数相加和为n.;第12个是分母为1的最后一个,第22个是分母为2的最后一个……,第n2个是分母为n的最后一个;
(1)因为1+3+5+…+2n﹣1=n2,
所以令n2≤800,
解得:n≤28,
当n=28时,n2=784,
所以第784个数是分母为28的最后一个数,
所以800个数的分母为29,分子为800﹣784=16,所以第800个数为;
(2)因为162+5=256+5=261,
172﹣4=289﹣4=285,
所以是第261个数或第285个数;
(3)令n2≤552,
解得:n≤23,
当n=23时,n2=529,
即前529个数的和为:1+2+3+……+23=24×11+12=276,
第530至第552个数之间一共有:
552﹣530+1=23个数,
第530至第552个数的和为:
11.5,
所以前552个数的和是:276+11.5=287.5;
(4)分母为n时,前n2个数的和为,当n=14时,前142=196个数的和为:
105,
第197个数开始为分母是15的数:
1,
105+1=106,
所以存在前n个数的和等于106,此时n=196+5=201。
故答案为:(1);(2)第261个数或第285个数;(3)287.5;(4)存在前n个数的和等于106,此时n的值是201。
【点评】解决本题的关键是找出规律,解决问题。
39.【答案】见试题解答内容
【分析】摆1个六边形需要6根小棒,可以写作:5×1+1;摆2个需要11根小棒,可以写作:5×2+1;摆3个需要16根小棒,可以写成:5×3+1;…由此可以推理得出一般规律解答问题.
【解答】解:根据题干分析可得:摆1个六边形需要6根小棒,可以写作:5×1+1;
摆2个需要11根小棒,可以写作:5×2+1;
摆3个需要小棒:5×3+1=16;
摆n个需要小棒:5×n+1=5n+1;
当n=8时,5n+1=5×8+1=41;
答:图⑧一共需要41根小棒.
【点评】根据题干中已知的图形的排列特点及其数量关系,推理得出一般的结论进行解答,是此类问题的关键.
40.【答案】32张
【分析】第1个“T”用了5张水果卡片,第2个“T”用了8张水果卡片,第3个“T”用了11张水果卡片;5=3+2,8=3×2+2,11=3×3+2,所以第10个“T”字要用(3×10+2)张水果卡片。
【解答】解:3×10+2=32(张)
答:第10个“T”字要用32张水果卡片。
【点评】观察图形,探索图形的排列规律,根据图形中水果卡片的张数与项数的关系解决问题。
41.【答案】见试题解答内容
【分析】(1)由裁剪时x张用A方法,其余用(19﹣x)张就用B方法,据此即可分别表示出裁剪出的侧面和底面的个数;
(2)由侧面个数与底面个数比是3:2建立方程求出x的值,求出侧面的总数即可解答问题.
【解答】解:(1)因为裁剪时x张用A方法,所以剪裁时(19﹣x)张用B方法;
那么侧面的个数是:6x+4(19﹣x)=6x+76﹣4x=2x+76(个)
底面个数是:5(19﹣x)=95﹣5x(个)
(2)由题意可得:(2x+76):(95﹣5x)=3:@
解得x=7
所以盒子的个数是:30(个)
答:能做30个盒子.
【点评】本题考查了列一元一次方程解决实际问题的应用,解答时根据侧面个数与底面个数的比建立方程是解决本题的关键.
42.【答案】11,13;41,2n+1。
【分析】摆1个三角形要3根小棒,即2×1+1;
摆2个三角形要5根小棒,即2×2+1;
……
摆n个三角形需要的小棒数为:2n+1。
【解答】解:(1)2×5+1
=10+1
=11(根)
2×6+1
=12+1
=13(根)
(2)2×20+1
=40+1
=41(根)
摆n个三角形要用(2n+1)根小棒。
故答案为:11,13;41,2n+1。
【点评】本题主要考查数与形结合的规律,发现每多1个三角形就多2根小棒是解本题的关键。
43.【答案】(1)18人;(2)(2+4m)人;(3)10张。
【分析】一张餐桌可摆放2+4×1=6把椅子,可以坐6人;
两张餐桌可摆放2+4×2=10把椅子,可以坐10人;
三张餐桌可摆放2+4×3=14把椅子,可以坐14人;
所以n张餐桌可摆放2+4n把椅子,可以坐(2+4n)人;根据此解答即可。
【解答】解:(1)2+4×4=18(人)
答:四张餐桌可坐18人。
(2)按照这个规律摆放,m张餐桌可以坐(2+4m)人。
(3)2+4m=42,可得:m=10(张)
答:需要10张餐桌。
故答案为:(1)18人;(2)(2+4m)人;(3)10张。
【点评】本题考查了数与形结合的规律,关键是能根据求出的结果或观察图形得出规律。
44.【答案】见试题解答内容
【分析】(1)观察图形可得:第一幅图中有1个点;第二幅图中有1+2=3个点;第三幅图中有1+2+3=6个点,可以写成(32+3);第四幅图中有1+2+3+4=10个点,可以写成(42+4)由此可得第8个图形中的点数为:1+2+3+…+8(82+8)=36个点.
(2)结合(1)分析发现规律:第n个图形中有1+2+3+…+n(n2+n)个点.
【解答】解:(1)根据题干分析可得:
第8个图形中的点数为:
1+2+3+…+8
(82+8)
=36(个).
答:第8个图形中有36个点.
(2)结合(1)分析发现:
第n个图形中的点数为:1+2+3+…+n(n2+n)
答:第n个图形中有(n2+n)个点.
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力.解决此类问题的关键是:根据题干中的图形找出事物排列的一般规律.
45.【答案】见试题解答内容
【分析】由题意可知,最外层每边是54÷6=9(棵),每边不包括三角形顶点外9﹣2=7(棵),最外层一共载7×3+3=24(棵).第二层是边长为30米的等边三角形,用同样的方法即可求出一共有多少棵.再算出第三层、第四层(一共四层)棵数,进而计算出总棵数,用总棵数乘2就是小时姐姐共带的同学数.
【解答】解:如图
最外层:7×3+3=24(棵)
第二层:4×3+3=15(棵)
第三层:2×3+3=9(棵)
第四层:1棵
(24+15+9+1)×2
=49×2
=98(名)
答:小时姐姐共带了98名同学.
【点评】解答此题的关键,也是难点,是求出石榴树的总棵数.
46.【答案】见试题解答内容
【分析】根据题意得到摆1个三角形所需火柴棍的根数是3,2个三角形所需火柴棍的根数是5=3+2×1,3个三角形所需火柴棍的根数是7=3+2×2,…,于是得到摆15个三角形所需火柴棍的根数=3+2×14=31,进而可得摆n个三角形所需火柴棍的根数是3+2(n﹣1)=2n+1,n为正整数,据此解答.
【解答】解:(1)3+2×14
=3+28
=31(根);
(2)由分析可知:
摆n个三角形所需火柴棍的根数是(2n+1),n为正整数,
2n+1=79
2n=78
n=39
答:摆15个三角形需要31根小棒;用79根小棒可以摆39个三角形.
【点评】本题考查了数与形结合的规律,解决本题先由已知条件找到一般规律,再根据规律求解.
47.【答案】13,18,28,38;(5n+3),(10n+8)。
【分析】(1)根据所给图示发现,第一个图形正方形的个数为:5+3=8(个),周长为:10+8=18;第二个图形正方形的个数为:5×2+3=13(个),周长为:10×2+8=28;第三个图形正方形的个数为:5×3+3=18(个),周长为:10×3+8=38;据此完成填表。
(2)根据(1)中的数据总结规律,完成填空即可。
【解答】解:(1)第一个图形正方形的个数为:5+3=8(个),周长为:10+8=18;
第二个图形正方形的个数为:5×2+3=13(个),周长为:10×2+8=28;
第三个图形正方形的个数为:5×3+3=18(个),周长为:10×3+8=38;
填表如下:
图形 ① ② ③
正方形的个数 8 13 18
图形的周长 18 28 38
(2)推测第n个图形中,正方形的个数为(5n+3),周长为(10n+8)。
故答案为:13,18,28,38;(5n+3),(10n+8)。
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力。
48.【答案】我发现后面的算式会循环出现7641﹣1467=6174。
【分析】按要求任意写一个四位数,将这个四位数的四个数字重新组合,组成一个最大的数和一个最小的数,用大数减去小数,重复进行,找出规律。
【解答】解:根据题意举例解答。如1234。
4321﹣1234=3087
8730﹣3078=5652
6552﹣2556=3996
9963﹣3699=6264
6642﹣2466=4176
7641﹣1467=6174
7641﹣1467=6174
我发现后面的算式会循环出现7641﹣1467=6174。
【点评】本题主要考查数列中的规律,找到规律是解题的规律。
49.【答案】37.5厘米。
【分析】1个杯子的高度是15cm,把5个完全一样的杯子叠起来的高度是25cm,那么上面每个杯子露出(25﹣15)÷4=2.5(厘米),然后求出上面9个杯子露出的高度,再加上15厘米即可。
【解答】解:(25﹣15)÷4
=10÷4
=2.5(厘米)
2.5×(10﹣1)+15
=22.5+15
=37.5(厘米)
答:10个这样的杯子叠起来的高度是37.5厘米。
【点评】本题考查数和形中的找规律问题,找到共同特征解决问题即可。
50.【答案】见试题解答内容
【分析】根据图意,每一行从左到右,箭尾部的“∧”依次减少1个,且箭头的指向左右相反,进而选出答案即可.
【解答】解:根据图意,每一行从左到右,箭尾部的“∧”依次减少1个,且箭头的指向左右相反,
故选D.
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力.
51.【答案】见试题解答内容
【分析】观察题干可知,前面的两个图形中,上面数字之和等于第三个图形的上面数字;所以可得:右面的两个数字之和,也等于第三个图形中的右面数字,据此即可解答.
【解答】解:根据题干分析可得:12+12=24
16+10=26
故答案为:
【点评】主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.
52.【答案】(1)4000
(2)1000
【分析】(1)利用长方形面积公式:S=ab,计算人行道的面积,然后用人行道的面积除以每块地砖的面积,就是所需块数.
(2)根据图形的排列规律,每4×4=16(块)方砖中,有4块是红色的,求所需地砖块数包含几个16,再乘4,计算所需红色地砖的块数即可.
【解答】解:(1)400×1.6÷0.42
=640÷0.16
=4000(块)
答:铺设这条人行道一共需4000块地砖.
(2)4000÷16×4
=250×4
=1000(块)
答:铺设这条人行道一共需要1000块红色地砖.
【点评】本题主要考查数与形结合的规律,关键是根据图示发现地砖排列的规律.
53.【答案】这本书共有15页插图。
【分析】因为插图和文字按页排列为文、文、图、图、图、文、文、图、图、图、文……所以,可知显示出周期循环的特点,按照文、文、图、图、图5页一个循环。27中有5个循环,剩下的第26,27页分别是文、文。据此答题即可。
【解答】解:经分析得:
27÷5=5……2
5×3=15(页)
答:这本书共有15页插图。
【点评】本题考查简单周期问题。结合发现的规律,利用带余除法解决问题即可。
54.【答案】(1)(2x+4)人。
(2)34人。
(3)28张。
【分析】摆1张长方形桌子可以坐6个人,6=2×3,
摆2张长方形桌子可以坐8个人,8=2×4,
摆3张长方形桌子可以坐10个人,10=2×5,
……
摆x张长方形桌子可以坐的人数:2(x+2)=2x+4。
【解答】解:(1)x张桌子可以坐(2x+4)人。
(2)当x=15时,
2×15+4
=30+4
=34(人)
答:当x=15时,一共可以坐34人。
(3)2x+4=60
2x=56
x=28
答:摆28张桌子可以坐60人。
【点评】本题主要考查数与形结合的规律,发现每多1张桌子就多坐2人是解本题的关键。
55.【答案】20;32。
【分析】根据图示可知,摆一个独立的图形长方体需要4根小棒,第几个图形就摆几个长方形,据此利用乘法计算小棒的根数即可。
【解答】解:5×4=20(根)
8×4=32(根)
答:第5个图形有20根小棒;第8个图形有32根小棒。
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力。
56.【答案】3;BC;135平方厘米。
【分析】(1)通过观察统计图可知,点E从点A开始,3秒钟后到达点B。
(2)统计图中3秒到8秒表示点E在长方形边BC上移动。
(3)根据长方形的面积公式:S=ab,把数据代入公式解答。
【解答】解:(1)点E从点A开始,3秒钟后到达点B。
(2)统计图中3秒到8秒表示点E在长方形边BC上移动。
8﹣3=5(秒)
(3×5)×(3×3)
=15×9
=135(平方厘米)
答:长方形ABCD的面积是135平方厘米。
故答案为:3;BC。
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
57.【答案】见试题解答内容
【分析】(1)观察图形可知,第一个图形黑色三角形有1个,白色三角形1+2=3个;第二个图形黑色三角形有1+2=3个,白色三角形1+2+3=6个;第三个图形黑色三角形有1+2+3=6个,白色三角形1+2+3+4=10个;则第四个图形黑色三角形有1+2+3+4=10个,白色三角形1+2+3+4+5=15个;据此画图即可;
(2)由上述推算可得:第n个图形黑色三角形有1+2+3+…n个,据此即可解答问题.
【解答】解:(1)根据题干分析可得:
(2)第n个图形黑色三角形有1+2+3+…n个,
当n=10时
黑色三角形的个数是:55(个)
答:第10个图形中有 55块黑色的瓷砖.
故答案为:55.
【点评】主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.
58.【答案】20根。
【分析】求搭4个这样独立的五边形需要多少根小棒,就相当于求4个5是多少,用乘法计算。
【解答】解:5×4=20(根)
答:搭4个这样独立的五边形需要20根小棒。
【点评】本题解答依据是:求几个相同加数的和,用乘法计算。
