河北省部分高中2023-2024学年高二上学期期中考试数学试题(含解析)
文档属性
| 名称 | 河北省部分高中2023-2024学年高二上学期期中考试数学试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 843.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-11 12:04:23 | ||
图片预览




文档简介
绝密★启用前
河北省部分高中2023-2024学年高二上学期期中考试
数 学
注意事项:
1.答题前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.本试卷主要考试内容;人教A版选择性必修第一册第一章至第三章3.2。
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.直线l:的斜率为
A. B. C. D.
2.若方程表示一个圆,则m的取值范围是
A. B. C. D.
3.已知,分别是椭圆E:的左、右焦点,P是椭圆E上一点,若,则
A.2 B.3 C.4 D.5
4.如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,且,则在方向上的投影向量为
A. B. C. D.
5.若圆:与圆:相交,则r的取值范围为
A. B. C. D.
6.若,,,则点A到直线BC的距离为
A. B. C. D.
7.已知双曲线C:的右焦点为F,过F作双曲线C的其中一条渐近线l的垂线,垂足为A(第一象限),并与双曲线C交于点B,若,则l的斜率为
A.2 B.1 C. D.
8.已知实数x,y满足,则的最小值为
A. B. C.108 D.117
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
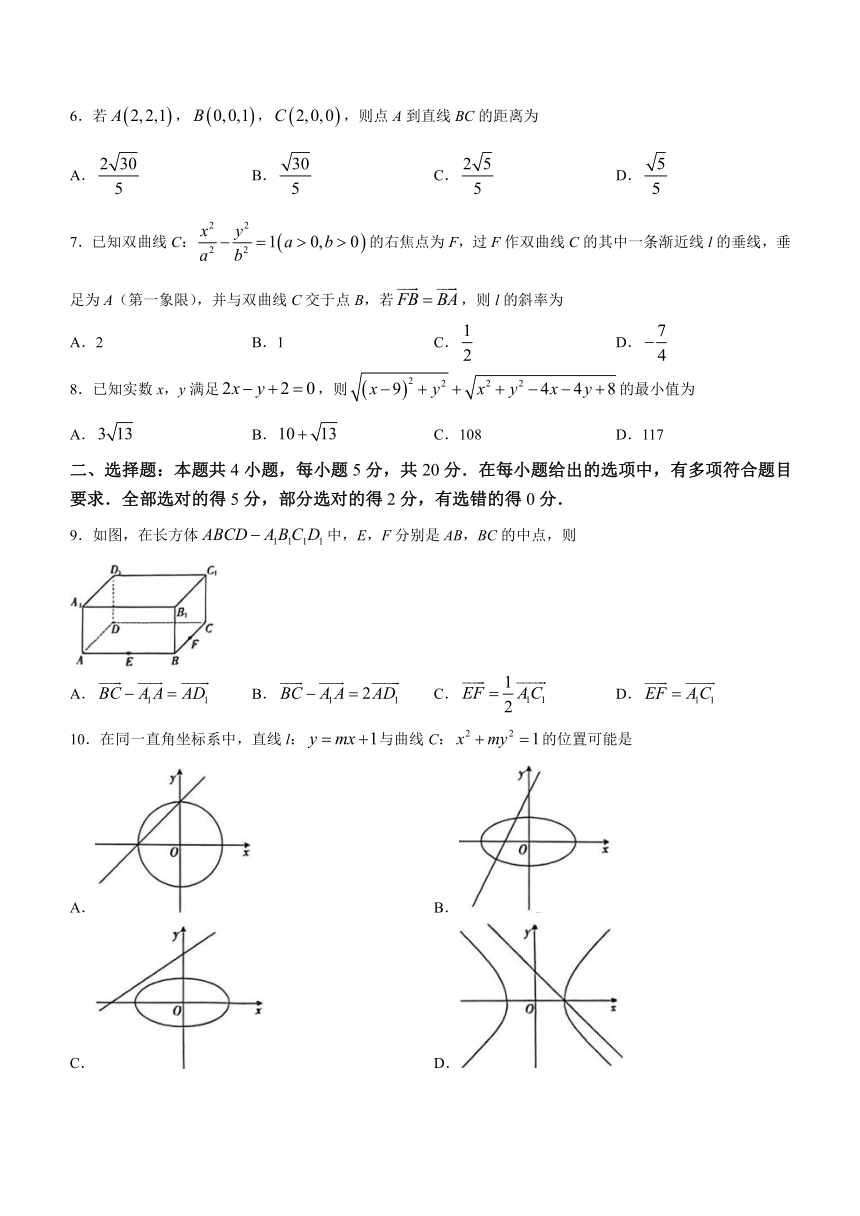
9.如图,在长方体中,E,F分别是AB,BC的中点,则
A. B. C. D.
10.在同一直角坐标系中,直线l:与曲线C:的位置可能是
A. B.
C. D.
11.已知,分别是椭圆E:的左、右焦点,P是椭圆E上一点,且,,则下列结论正确的有
A.椭圆E的离心率为
B.椭圆E的离心率为
C.
D.若内切圆的半径为2,则椭圆E的焦距为10
12.苏州博物馆(图一)是地方历史艺术性博物馆,建筑物的顶端可抽象为如图二所示的上、下两
层等高的几何体,其中上层EFGH-NPQM是正四棱柱,下层底面ABCD是边长为4的正方形,E,F,G,H在底面ABCD的投影分别为AD,AB,BC,CD的中点,若,则下列结论正确的有
图一 图二
A.该几何体的表面积为
B.将该几何体放置在一个球体内,则该球体体积的最小值为
C.直线CP与平面ABF所成角的正弦值为雪
D.点M到平面BFG的距离为
三、填空题:本题共4小题,每小题5分,共20分.
13.已知点N是点在坐标平面Oxz内的射影,则 .
14.若双曲线C:的实轴长与虚轴长相等,则 .
15.过点作圆C:的两条切线,切点分别为A,B,则直线AB的方程为 .
16.如图,在正方体中,,N为的中点,记平面CMN与平面的交线为l,则直线l与直线所成角的余弦值为 .
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)
已知直线:与:.
(1)当时,求直线与的交点坐标;
(2)若,求a的值.
18.(12分)
如图,在正四棱锥P-ABCD中,E,F分别为PA,PC的中点,.
(1)证明:B,E,G,F四点共面.
(2)记四棱锥P-BEGF的体积为,四棱锥P-ABCD的体积为,求的值.
19.(12分)
已知P是圆C:上一动点,过P作x轴的垂线,垂足为Q,点M满足,记点M的轨迹为E.
(1)求E的方程;
(2)若A,B是E上两点,且线段AB的中点坐标为,求的值.
20.(12分)
如图,这是某圆弧形山体隧道的示意图,其中底面AB的长为16米,最大高度CD的长为4米,以C为坐标原点,AB所在的直线为x轴建立直角坐标系.
(1)求该圆弧所在圆的方程;
(2)若某种汽车的宽约为2.5米,高约为1.6米,车辆行驶时两车的间距要求不小于0.5米以保证安全,同时车顶不能与隧道有剐蹭,则该隧道最多可以并排通过多少辆该种汽车?(将汽车看作长方体)
21.(12分)
如图,在斜三棱柱中,△ABC是边长为2的等边三角形,M,Q分别为AC,的中点,且.
(1)证明:.
(2)若,,求平面与平面夹角的余弦值.
22.(12分)
如图,已知,分别是双曲线E:的左、右焦点,是E上一点.
(1)求E的方程.
(2)过直线l:上任意一点T作直线,与E的左、右两支相交于A,B两点,直线关于直线l对称的直线为(与不重合),与E的左、右两支相交于C,D两点.证明:.
河北省部分高中2023-2024学年高二上学期期中考试
数学参考答案
1.D
【解析】本题考查直线的斜率,考查数学抽象的核心素养.
将l的方程转化为,知l的斜率为.
2.B
【解析】本题考查圆的一般式方程,考查数学运算的核心素养.
因为方程表示一个圆,所以,解得.
3.C
【解析】本题考查椭圆的基本概念,考查数学抽象的核心素养.
因为P是椭圆E上一点,所以,所以.
4.C
【解析】本题考查空间向量的投影向量,考查直观想象的核心素养.
由图可知,在方向上的投影向量为.
5.D
【解析】本题考查圆与圆的位置关系,考查数学运算的核心素养.
因为与相交,所以.又,所以,解得.
6.A
【解析】本题考查空间中点到直线的距离,考查数学运算的核心素养.
,,则在上的投影向量的模为,则点A到直线BC的距离为.
7.B
【解析】本题考查双曲线的性质,考查数学运算的核心素养.
因为,所以B为线段AF的中点,则.设双曲线C的左焦点为,则.在中,,整理得,即,则,故l的斜率为1.
8.A
【解析】本题考查直线的对称问题,考查直观想象与数学运算的核心素养.
,所以表示直线l:上一点到,两点距离之和的最小值.易知P,Q两点在l的同一侧,设点P关于l对称的点,则,解得,即,故.
9.AC
【解析】本题考查空间向量的线性运算,考查数学运算、直观想象的核心素养.
,A正确,B不正确.,C正确,D不正确.
10.ABD
【解析】本题考查直线与曲线的位置关系,考查直观想象与逻辑推理的核心素养.
若,则曲线C表示坐标原点为圆心,1为半径的圆,并且l与C相交于,两点,A符合.若,则曲线C表示焦点在.轴上的椭圆,并且l与C相交,B符合,C不符合.若,则曲线C表示焦点在y轴上的椭圆,没有符合的选项.当时,曲线C表示焦点在x轴上的双曲线,直线l经过第一、二、四象限,且l经过曲线C的右顶点,D符合.
11.ACD
【解析】本题考查椭圆的性质,考查数学运算、逻辑推理的核心素养.
由,,解得,,则
,整理得,
即,则(舍去)或,故椭圆E的离心率为.A正确,B不正确.由,得,则,故.C正确.由,内切圆的半径为2,得.因为,所以,即椭圆E的焦距为10.D正确.
12.ACD
【解析】本题考查立体几何中直线与平面所成角的正弦值,考查直观想象的核心素养.
因为F在平面ABCD的投影为AB的中点,且,,所以F到平面ABCD的距离为1,,P到平面ABCD的距离为2,则点B到FG的距离为,则△ABF的面积为,△BFG的面积为长.根据对称性可知,该几何体的表面积为.A正确.将该几何体放置在一个球体内,要使该球体体积最小,则球心在该几何体上下底面中心所连直线上,且A,B,C,D,N,P,Q,M均在球面上,设球心到下底面ABCD的距离为x,则,解得,则该球体的半径为,体积为.B不正确.以A为坐标原点建立如图所示的空间直角坐标系,则,,,,,,,,,,平面ABF的一个法向量为,则,故直线CP与平面ABF所成角的正弦值为.C正确.设平面BFG的法向量为,则,令,得,则点M到平面BFG的距离为.D正确.
13.5
【解析】本题考查空间向量的模,考查数学运算的核心素养.
由题可知,,则,.
14.1
【解析】本题考查双曲线的概念,考查数学运算的核心素养.
由题可知,,解得或(舍去).
15.
【解析】本题考查圆的切线,考查直观想象的核心素养.
由图(图略)可知,其中一条切线为x轴,切点为坐标原点.因为,则,直线AB的方程为.
16.
【解析】本题考查直线与直线的夹角,考查直观想象﹑数学运算的核心素养.
设,连接NP,MP(图略),则直线NP即直线l.易证得,由,N为的中点,得.以D为坐标原点,DA,DC,所在直线分别为x,y,z轴建立空间直角坐标系,不妨令,则,,,,,,,故直线l与直线所成角的余弦值为.
17.解:
(1)因为,所以:,:.
联立方程组,
解得,
故直线与的交点坐标为.
(2)因为,所以,解得或.
当时,与重合,不符合题意.
当时,与不重合,符合题意.
故.
18.
(1)证明:设为空间的一组基底,因为E,F分别为PA,PC的中点,所以,.
又,所以.
故B,E,G,F四点共面.
(2)解:由正四棱锥的对称性知,,.
设点E到平面PBG的距离为,点A到平面PBD的距离为,由E是PA的中点得.
由,得,
则.
19.解:
(1)设,则.
因为P在圆C上,所以,
故E的方程为.
(2)设,,则,
两式相减得,即.
因为线段AB的中点坐标为,所以,所以直线AB的方程为.
联立方程组,整理得,则,,
.
20.解:
(1)由圆的对称性可知,该圆弧所在圆的圆心在y轴上,
设该圆的半径为r米,则,解得,
故该圆弧所在圆的方程为.
(2)设与该种汽车等高且能通过该隧道的最大宽度为d米,则,
解得.
若并排通过5辆该种汽车,则安全通行的宽度为,故该隧道不能并排通过5辆该种汽车.
若并排通过4辆该种汽车,则安全通行的宽度为.隧道能并排通过4辆该种汽车.
综上所述,该隧道最多可以并排通过4辆该种汽车.
21.
(1)证明:因为是等边三角形,Q为的中点,所以.
又,所以.
因为,,所以平面.
又平面,所以.
(2)解:取AB靠近点A的四等分点N,连接MN,NQ,易证得,则,且.
由,得.因为,所以,即,从而平面ABC.
以M为坐标原点,MN所在直线为x轴,MQ所在直线为z轴,建立如图所示的空间直角坐标系,
则,,,
则,.
设平面的法向量为,则,
令,得.
由图可知,是平面的一个法向量.
设平面与平面的夹角为,则.
22.
(1)解:由题可知,
解得,,
则E的方程为.
(2)证明:设,显然直线的斜率存在且不等于0,设的方程为,则直线的方程,设,,,.
联立方程组,
整理得.
,
则,.
同理可得,,
,,,,
则,
同理可得,则,
则,则,即.
河北省部分高中2023-2024学年高二上学期期中考试
数 学
注意事项:
1.答题前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.本试卷主要考试内容;人教A版选择性必修第一册第一章至第三章3.2。
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.直线l:的斜率为
A. B. C. D.
2.若方程表示一个圆,则m的取值范围是
A. B. C. D.
3.已知,分别是椭圆E:的左、右焦点,P是椭圆E上一点,若,则
A.2 B.3 C.4 D.5
4.如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,且,则在方向上的投影向量为
A. B. C. D.
5.若圆:与圆:相交,则r的取值范围为
A. B. C. D.
6.若,,,则点A到直线BC的距离为
A. B. C. D.
7.已知双曲线C:的右焦点为F,过F作双曲线C的其中一条渐近线l的垂线,垂足为A(第一象限),并与双曲线C交于点B,若,则l的斜率为
A.2 B.1 C. D.
8.已知实数x,y满足,则的最小值为
A. B. C.108 D.117
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.如图,在长方体中,E,F分别是AB,BC的中点,则
A. B. C. D.
10.在同一直角坐标系中,直线l:与曲线C:的位置可能是
A. B.
C. D.
11.已知,分别是椭圆E:的左、右焦点,P是椭圆E上一点,且,,则下列结论正确的有
A.椭圆E的离心率为
B.椭圆E的离心率为
C.
D.若内切圆的半径为2,则椭圆E的焦距为10
12.苏州博物馆(图一)是地方历史艺术性博物馆,建筑物的顶端可抽象为如图二所示的上、下两
层等高的几何体,其中上层EFGH-NPQM是正四棱柱,下层底面ABCD是边长为4的正方形,E,F,G,H在底面ABCD的投影分别为AD,AB,BC,CD的中点,若,则下列结论正确的有
图一 图二
A.该几何体的表面积为
B.将该几何体放置在一个球体内,则该球体体积的最小值为
C.直线CP与平面ABF所成角的正弦值为雪
D.点M到平面BFG的距离为
三、填空题:本题共4小题,每小题5分,共20分.
13.已知点N是点在坐标平面Oxz内的射影,则 .
14.若双曲线C:的实轴长与虚轴长相等,则 .
15.过点作圆C:的两条切线,切点分别为A,B,则直线AB的方程为 .
16.如图,在正方体中,,N为的中点,记平面CMN与平面的交线为l,则直线l与直线所成角的余弦值为 .
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)
已知直线:与:.
(1)当时,求直线与的交点坐标;
(2)若,求a的值.
18.(12分)
如图,在正四棱锥P-ABCD中,E,F分别为PA,PC的中点,.
(1)证明:B,E,G,F四点共面.
(2)记四棱锥P-BEGF的体积为,四棱锥P-ABCD的体积为,求的值.
19.(12分)
已知P是圆C:上一动点,过P作x轴的垂线,垂足为Q,点M满足,记点M的轨迹为E.
(1)求E的方程;
(2)若A,B是E上两点,且线段AB的中点坐标为,求的值.
20.(12分)
如图,这是某圆弧形山体隧道的示意图,其中底面AB的长为16米,最大高度CD的长为4米,以C为坐标原点,AB所在的直线为x轴建立直角坐标系.
(1)求该圆弧所在圆的方程;
(2)若某种汽车的宽约为2.5米,高约为1.6米,车辆行驶时两车的间距要求不小于0.5米以保证安全,同时车顶不能与隧道有剐蹭,则该隧道最多可以并排通过多少辆该种汽车?(将汽车看作长方体)
21.(12分)
如图,在斜三棱柱中,△ABC是边长为2的等边三角形,M,Q分别为AC,的中点,且.
(1)证明:.
(2)若,,求平面与平面夹角的余弦值.
22.(12分)
如图,已知,分别是双曲线E:的左、右焦点,是E上一点.
(1)求E的方程.
(2)过直线l:上任意一点T作直线,与E的左、右两支相交于A,B两点,直线关于直线l对称的直线为(与不重合),与E的左、右两支相交于C,D两点.证明:.
河北省部分高中2023-2024学年高二上学期期中考试
数学参考答案
1.D
【解析】本题考查直线的斜率,考查数学抽象的核心素养.
将l的方程转化为,知l的斜率为.
2.B
【解析】本题考查圆的一般式方程,考查数学运算的核心素养.
因为方程表示一个圆,所以,解得.
3.C
【解析】本题考查椭圆的基本概念,考查数学抽象的核心素养.
因为P是椭圆E上一点,所以,所以.
4.C
【解析】本题考查空间向量的投影向量,考查直观想象的核心素养.
由图可知,在方向上的投影向量为.
5.D
【解析】本题考查圆与圆的位置关系,考查数学运算的核心素养.
因为与相交,所以.又,所以,解得.
6.A
【解析】本题考查空间中点到直线的距离,考查数学运算的核心素养.
,,则在上的投影向量的模为,则点A到直线BC的距离为.
7.B
【解析】本题考查双曲线的性质,考查数学运算的核心素养.
因为,所以B为线段AF的中点,则.设双曲线C的左焦点为,则.在中,,整理得,即,则,故l的斜率为1.
8.A
【解析】本题考查直线的对称问题,考查直观想象与数学运算的核心素养.
,所以表示直线l:上一点到,两点距离之和的最小值.易知P,Q两点在l的同一侧,设点P关于l对称的点,则,解得,即,故.
9.AC
【解析】本题考查空间向量的线性运算,考查数学运算、直观想象的核心素养.
,A正确,B不正确.,C正确,D不正确.
10.ABD
【解析】本题考查直线与曲线的位置关系,考查直观想象与逻辑推理的核心素养.
若,则曲线C表示坐标原点为圆心,1为半径的圆,并且l与C相交于,两点,A符合.若,则曲线C表示焦点在.轴上的椭圆,并且l与C相交,B符合,C不符合.若,则曲线C表示焦点在y轴上的椭圆,没有符合的选项.当时,曲线C表示焦点在x轴上的双曲线,直线l经过第一、二、四象限,且l经过曲线C的右顶点,D符合.
11.ACD
【解析】本题考查椭圆的性质,考查数学运算、逻辑推理的核心素养.
由,,解得,,则
,整理得,
即,则(舍去)或,故椭圆E的离心率为.A正确,B不正确.由,得,则,故.C正确.由,内切圆的半径为2,得.因为,所以,即椭圆E的焦距为10.D正确.
12.ACD
【解析】本题考查立体几何中直线与平面所成角的正弦值,考查直观想象的核心素养.
因为F在平面ABCD的投影为AB的中点,且,,所以F到平面ABCD的距离为1,,P到平面ABCD的距离为2,则点B到FG的距离为,则△ABF的面积为,△BFG的面积为长.根据对称性可知,该几何体的表面积为.A正确.将该几何体放置在一个球体内,要使该球体体积最小,则球心在该几何体上下底面中心所连直线上,且A,B,C,D,N,P,Q,M均在球面上,设球心到下底面ABCD的距离为x,则,解得,则该球体的半径为,体积为.B不正确.以A为坐标原点建立如图所示的空间直角坐标系,则,,,,,,,,,,平面ABF的一个法向量为,则,故直线CP与平面ABF所成角的正弦值为.C正确.设平面BFG的法向量为,则,令,得,则点M到平面BFG的距离为.D正确.
13.5
【解析】本题考查空间向量的模,考查数学运算的核心素养.
由题可知,,则,.
14.1
【解析】本题考查双曲线的概念,考查数学运算的核心素养.
由题可知,,解得或(舍去).
15.
【解析】本题考查圆的切线,考查直观想象的核心素养.
由图(图略)可知,其中一条切线为x轴,切点为坐标原点.因为,则,直线AB的方程为.
16.
【解析】本题考查直线与直线的夹角,考查直观想象﹑数学运算的核心素养.
设,连接NP,MP(图略),则直线NP即直线l.易证得,由,N为的中点,得.以D为坐标原点,DA,DC,所在直线分别为x,y,z轴建立空间直角坐标系,不妨令,则,,,,,,,故直线l与直线所成角的余弦值为.
17.解:
(1)因为,所以:,:.
联立方程组,
解得,
故直线与的交点坐标为.
(2)因为,所以,解得或.
当时,与重合,不符合题意.
当时,与不重合,符合题意.
故.
18.
(1)证明:设为空间的一组基底,因为E,F分别为PA,PC的中点,所以,.
又,所以.
故B,E,G,F四点共面.
(2)解:由正四棱锥的对称性知,,.
设点E到平面PBG的距离为,点A到平面PBD的距离为,由E是PA的中点得.
由,得,
则.
19.解:
(1)设,则.
因为P在圆C上,所以,
故E的方程为.
(2)设,,则,
两式相减得,即.
因为线段AB的中点坐标为,所以,所以直线AB的方程为.
联立方程组,整理得,则,,
.
20.解:
(1)由圆的对称性可知,该圆弧所在圆的圆心在y轴上,
设该圆的半径为r米,则,解得,
故该圆弧所在圆的方程为.
(2)设与该种汽车等高且能通过该隧道的最大宽度为d米,则,
解得.
若并排通过5辆该种汽车,则安全通行的宽度为,故该隧道不能并排通过5辆该种汽车.
若并排通过4辆该种汽车,则安全通行的宽度为.隧道能并排通过4辆该种汽车.
综上所述,该隧道最多可以并排通过4辆该种汽车.
21.
(1)证明:因为是等边三角形,Q为的中点,所以.
又,所以.
因为,,所以平面.
又平面,所以.
(2)解:取AB靠近点A的四等分点N,连接MN,NQ,易证得,则,且.
由,得.因为,所以,即,从而平面ABC.
以M为坐标原点,MN所在直线为x轴,MQ所在直线为z轴,建立如图所示的空间直角坐标系,
则,,,
则,.
设平面的法向量为,则,
令,得.
由图可知,是平面的一个法向量.
设平面与平面的夹角为,则.
22.
(1)解:由题可知,
解得,,
则E的方程为.
(2)证明:设,显然直线的斜率存在且不等于0,设的方程为,则直线的方程,设,,,.
联立方程组,
整理得.
,
则,.
同理可得,,
,,,,
则,
同理可得,则,
则,则,即.
同课章节目录
