2023-2024学年人教版数学八年级上册14.3因式分解 测试题 (含答案)
文档属性
| 名称 | 2023-2024学年人教版数学八年级上册14.3因式分解 测试题 (含答案) | 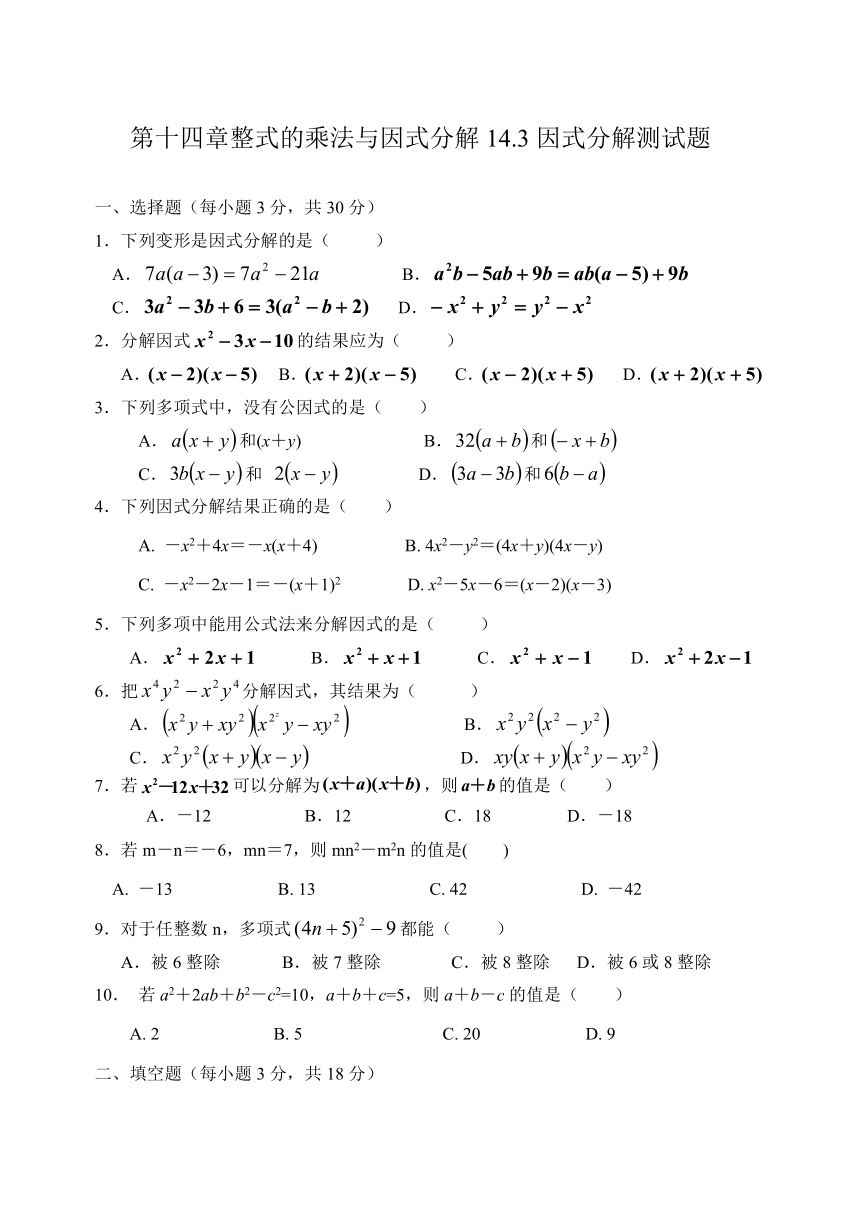 | |
| 格式 | docx | ||
| 文件大小 | 108.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-12 19:52:05 | ||
图片预览
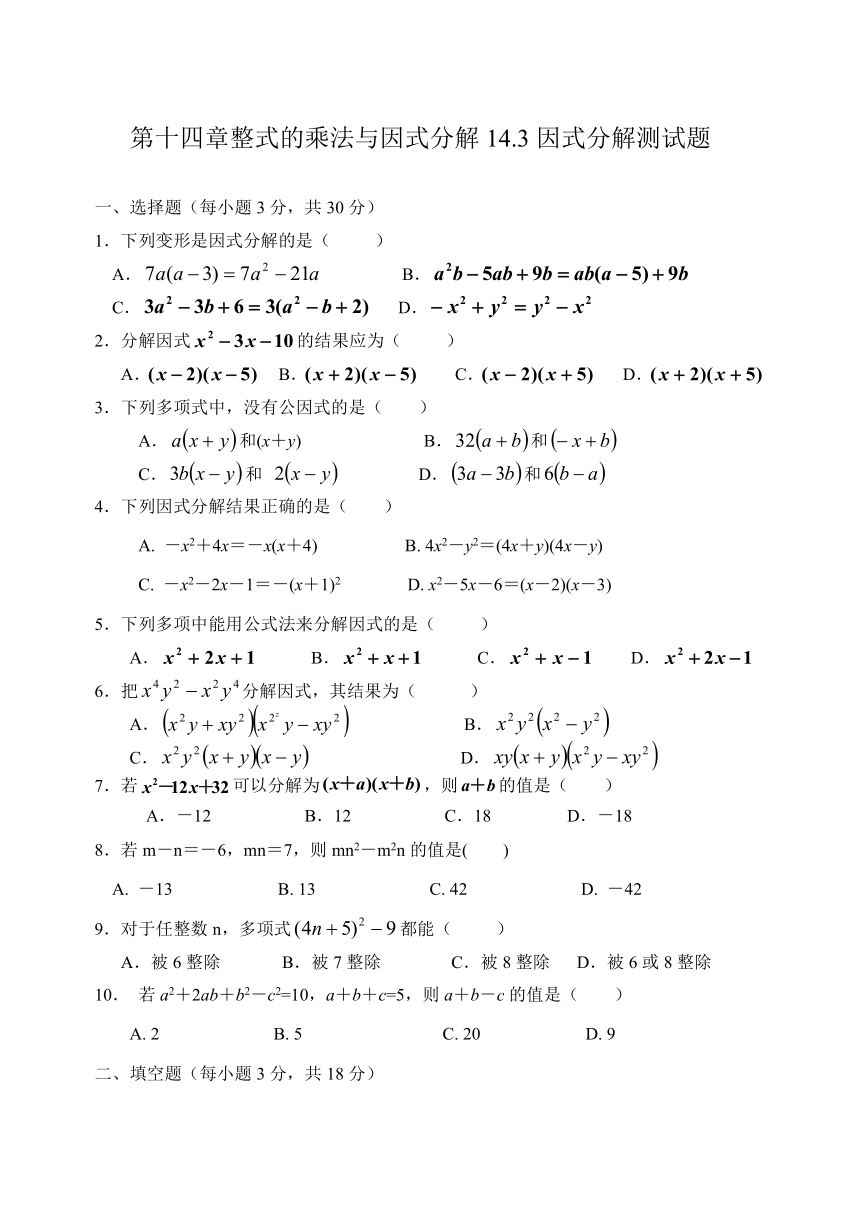


文档简介
第十四章整式的乘法与因式分解14.3因式分解测试题
一、选择题(每小题3分,共30分)
1.下列变形是因式分解的是( )
A. B.
C. D.
2.分解因式的结果应为( )
A. B. C. D.
3.下列多项式中,没有公因式的是( )
A.和(x+y) B.和
C.和 D.和
4.下列因式分解结果正确的是( )
A. -x2+4x=-x(x+4) B. 4x2-y2=(4x+y)(4x-y)
C. -x2-2x-1=-(x+1)2 D. x2-5x-6=(x-2)(x-3)
5.下列多项中能用公式法来分解因式的是( )
A. B. C. D.
6.把分解因式,其结果为( )
A. B.
C. D.
7.若可以分解为,则的值是( )
A.-12 B.12 C.18 D.-18
8.若m-n=-6,mn=7,则mn2-m2n的值是( )
A. -13 B. 13 C. 42 D. -42
9.对于任整数n,多项式都能( )
A.被6整除 B.被7整除 C.被8整除 D.被6或8整除
10. 若a2+2ab+b2-c2=10,a+b+c=5,则a+b-c的值是( )
A. 2 B. 5 C. 20 D. 9
二、填空题(每小题3分,共18分)
12.分解因式:x3-16x= .
12.分解因式: .
13.若一个正方形的面积为,则此正方形的周长为 .
14.若a+b=-1,则3a2+3b2+6ab的值是_____________.
15.若,,则a+b的值为 .
16.若m=2n+1,则的值是_________.
三、解答题(共72分)
17.(9分)分解因式:
(1) 8m2n+2mn (2) 12xyz-9x2y2 (3) 2a(y-z)-3b(z-y)
18.(9分)分解因式:
(1) a2-b2 (2) x2y-4y (3) -a4+16
19.(9分)分解因式:
(1) x2+12x+36 (2) 4x2-4x+1 (3) -3x2+6xy-3y2
20.(9分)分解因式:
(1); (2); (3).
21.(8分)用简便方法计算
(1)3.14×522-3.14×482 ; (2)6002-1200×598+5982
(10分)
(1)已知,,利用因式分解求的值.
(2)已知4x=3y,求代数式(x-2y)2-(x-y)(x+y)-2y2的值.
23.(8分)我们知道因式分解与整式乘法是互逆的关系,那么逆用乘法公式
(x+a)(x+b)=x2+(a+b)x+ab即x2+(a+b)x+ab=(x+a)(x+b)
是否可以分解因式呢?当然可以,而且也很简单.
如:x2+5x+6=x2+(3+2)x+3×2=(x+3)(x+2);
x2-5x-6=x2+(-6+1)x+(-6)×1=(x-6)(x+1).
请你仿照上述方法,把下列多项式分解因式:
(1)x2-8x+7 ;(2)x2+7x-18; (3) ; (4).
24. (12分)阅读下面的材料:
常用的分解因式的方法有提取公因式法、公式法等,但有的多项式只用上述方法无法分解,
如x2-4y2-2x+4y,细心观察这个式子,会发现前两项符合平方差公式,后两项可提取公因式,
前、后两部分分别因式分解后又出现新的公因式,提取公因式就可以完成整个式子的分解因式,
具体过程如下:
x2-4y2-2x+4y=(x2-4y2)-2(x-2y)=(x+2y)(x-2y)-2(x-2y)=(x-2y)(x+2y-2).
像这种将一个多项式适当分组后,进行分解因式的方法叫做分组分解法.
利用分组分解法解决下面的问题:
(1)分解因式:x2-2xy+y2-9;
(2)已知△ABC的三边长a、b、c满足ac-c2+bc-ab=0,
判断△ABC的形状并说明理由;
(3)在(2)的条件下,若a>c,∠BAC=90°,点D在线段BC上,
∠EDB=∠C,BE⊥DE,垂足为E,DE与AB相交于点F,
(
A
D
B
C
E
F
)若△BDF的面积为,求BE的长,
第十四章整式的乘法与因式分解14.3因式分解测试题
参考答案
一、选择题
1.C 2.B 3.B 4.C 5.A 6.C 7.A 8.C 9.C 10.A
二、填空题
11. 12. 13.
14.-3 15. 16.1
三、解答题
17.(1) 8m2n+2mn=2mn(4m+1)
(2) 12xyz-9x2y2=3xy(4z-3xy)
(3) 2a(y-z)-3b(z-y)=2a(y-z)+3b(y-z)=(y-z)(2a+3b)
18.(1) a2-b2=(a+b)(a-b)
(2) x2y-4y=y(x2-4) =y(x+2)(x-2)
(3) -a4+16=16-a4=(4+a2)(4-a2) =(4+a2)(2+a)(2-a)
19(1)原式= x2+2·x 6+62=(x+6)2
(2)原式=(2x)2-2·2x·1+1 =(2x-1)2
(3)原式= -3(x2-2xy+y2)= -3(x-y)2
20.(1);
(2);(6);
(3)
21.(1)1256; (2)4
22.
(1)原式;
因为,,所以,原式
原式=x2-4xy+4y2-(x2-y2)-2y2=-4xy+3y2=-y(4x-3y).
∵4x=3y,∴原式=0
23. 解:(1) (2);
(3) (4)
24.(1) x2-2xy+y2-9=(x-y)2-9=(x-y+3)(x-y-3);
(2) ∵ac-c2+bc-ab=0,∴(a-c)c-b(a-c)=0,∴(a-c)(c-b)=0,
∴a=c或b=c,∴△ABC为等腰三角形.
(3) 由(2)得a=c或b=c,又a>c,∴b=c.
又∵∠BAC=90°,∴△ABC为等腰直角三角形.
过D作DG∥AC交BE的延长线于G,
则△BDH为等腰直角三角形,DH=BH.
∠BHD=∠BEF=90°,
由内角和(八字型)得:∠FDH=∠GBH.
∴△DHF≌△BHG(ASA),∴DF=BG.
又∵∠EDB=∠C=∠BDH,∴∠BDE=∠GDE,
∴△BDE≌△GDE(ASA),∴BE=GE,∴DF=2BE.
由△BDF的面积为,得DF·BE=,∴BE2=,∴BE=.
一、选择题(每小题3分,共30分)
1.下列变形是因式分解的是( )
A. B.
C. D.
2.分解因式的结果应为( )
A. B. C. D.
3.下列多项式中,没有公因式的是( )
A.和(x+y) B.和
C.和 D.和
4.下列因式分解结果正确的是( )
A. -x2+4x=-x(x+4) B. 4x2-y2=(4x+y)(4x-y)
C. -x2-2x-1=-(x+1)2 D. x2-5x-6=(x-2)(x-3)
5.下列多项中能用公式法来分解因式的是( )
A. B. C. D.
6.把分解因式,其结果为( )
A. B.
C. D.
7.若可以分解为,则的值是( )
A.-12 B.12 C.18 D.-18
8.若m-n=-6,mn=7,则mn2-m2n的值是( )
A. -13 B. 13 C. 42 D. -42
9.对于任整数n,多项式都能( )
A.被6整除 B.被7整除 C.被8整除 D.被6或8整除
10. 若a2+2ab+b2-c2=10,a+b+c=5,则a+b-c的值是( )
A. 2 B. 5 C. 20 D. 9
二、填空题(每小题3分,共18分)
12.分解因式:x3-16x= .
12.分解因式: .
13.若一个正方形的面积为,则此正方形的周长为 .
14.若a+b=-1,则3a2+3b2+6ab的值是_____________.
15.若,,则a+b的值为 .
16.若m=2n+1,则的值是_________.
三、解答题(共72分)
17.(9分)分解因式:
(1) 8m2n+2mn (2) 12xyz-9x2y2 (3) 2a(y-z)-3b(z-y)
18.(9分)分解因式:
(1) a2-b2 (2) x2y-4y (3) -a4+16
19.(9分)分解因式:
(1) x2+12x+36 (2) 4x2-4x+1 (3) -3x2+6xy-3y2
20.(9分)分解因式:
(1); (2); (3).
21.(8分)用简便方法计算
(1)3.14×522-3.14×482 ; (2)6002-1200×598+5982
(10分)
(1)已知,,利用因式分解求的值.
(2)已知4x=3y,求代数式(x-2y)2-(x-y)(x+y)-2y2的值.
23.(8分)我们知道因式分解与整式乘法是互逆的关系,那么逆用乘法公式
(x+a)(x+b)=x2+(a+b)x+ab即x2+(a+b)x+ab=(x+a)(x+b)
是否可以分解因式呢?当然可以,而且也很简单.
如:x2+5x+6=x2+(3+2)x+3×2=(x+3)(x+2);
x2-5x-6=x2+(-6+1)x+(-6)×1=(x-6)(x+1).
请你仿照上述方法,把下列多项式分解因式:
(1)x2-8x+7 ;(2)x2+7x-18; (3) ; (4).
24. (12分)阅读下面的材料:
常用的分解因式的方法有提取公因式法、公式法等,但有的多项式只用上述方法无法分解,
如x2-4y2-2x+4y,细心观察这个式子,会发现前两项符合平方差公式,后两项可提取公因式,
前、后两部分分别因式分解后又出现新的公因式,提取公因式就可以完成整个式子的分解因式,
具体过程如下:
x2-4y2-2x+4y=(x2-4y2)-2(x-2y)=(x+2y)(x-2y)-2(x-2y)=(x-2y)(x+2y-2).
像这种将一个多项式适当分组后,进行分解因式的方法叫做分组分解法.
利用分组分解法解决下面的问题:
(1)分解因式:x2-2xy+y2-9;
(2)已知△ABC的三边长a、b、c满足ac-c2+bc-ab=0,
判断△ABC的形状并说明理由;
(3)在(2)的条件下,若a>c,∠BAC=90°,点D在线段BC上,
∠EDB=∠C,BE⊥DE,垂足为E,DE与AB相交于点F,
(
A
D
B
C
E
F
)若△BDF的面积为,求BE的长,
第十四章整式的乘法与因式分解14.3因式分解测试题
参考答案
一、选择题
1.C 2.B 3.B 4.C 5.A 6.C 7.A 8.C 9.C 10.A
二、填空题
11. 12. 13.
14.-3 15. 16.1
三、解答题
17.(1) 8m2n+2mn=2mn(4m+1)
(2) 12xyz-9x2y2=3xy(4z-3xy)
(3) 2a(y-z)-3b(z-y)=2a(y-z)+3b(y-z)=(y-z)(2a+3b)
18.(1) a2-b2=(a+b)(a-b)
(2) x2y-4y=y(x2-4) =y(x+2)(x-2)
(3) -a4+16=16-a4=(4+a2)(4-a2) =(4+a2)(2+a)(2-a)
19(1)原式= x2+2·x 6+62=(x+6)2
(2)原式=(2x)2-2·2x·1+1 =(2x-1)2
(3)原式= -3(x2-2xy+y2)= -3(x-y)2
20.(1);
(2);(6);
(3)
21.(1)1256; (2)4
22.
(1)原式;
因为,,所以,原式
原式=x2-4xy+4y2-(x2-y2)-2y2=-4xy+3y2=-y(4x-3y).
∵4x=3y,∴原式=0
23. 解:(1) (2);
(3) (4)
24.(1) x2-2xy+y2-9=(x-y)2-9=(x-y+3)(x-y-3);
(2) ∵ac-c2+bc-ab=0,∴(a-c)c-b(a-c)=0,∴(a-c)(c-b)=0,
∴a=c或b=c,∴△ABC为等腰三角形.
(3) 由(2)得a=c或b=c,又a>c,∴b=c.
又∵∠BAC=90°,∴△ABC为等腰直角三角形.
过D作DG∥AC交BE的延长线于G,
则△BDH为等腰直角三角形,DH=BH.
∠BHD=∠BEF=90°,
由内角和(八字型)得:∠FDH=∠GBH.
∴△DHF≌△BHG(ASA),∴DF=BG.
又∵∠EDB=∠C=∠BDH,∴∠BDE=∠GDE,
∴△BDE≌△GDE(ASA),∴BE=GE,∴DF=2BE.
由△BDF的面积为,得DF·BE=,∴BE2=,∴BE=.
