新人教版17.1勾股定理课件
文档属性
| 名称 | 新人教版17.1勾股定理课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 757.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-25 00:00:00 | ||
图片预览



文档简介
课件23张PPT。第十七章 勾股定理
17.1 勾股定理(3)藤县太平四中
莫素芳1.已知直角三角形ABC的三边为a、b、c , ∠C= 90°,则 a、b、c 三者之间的关系是 ;
2.若一个直角三角形两条直角边长是3和2,那么第三条边长是 ;
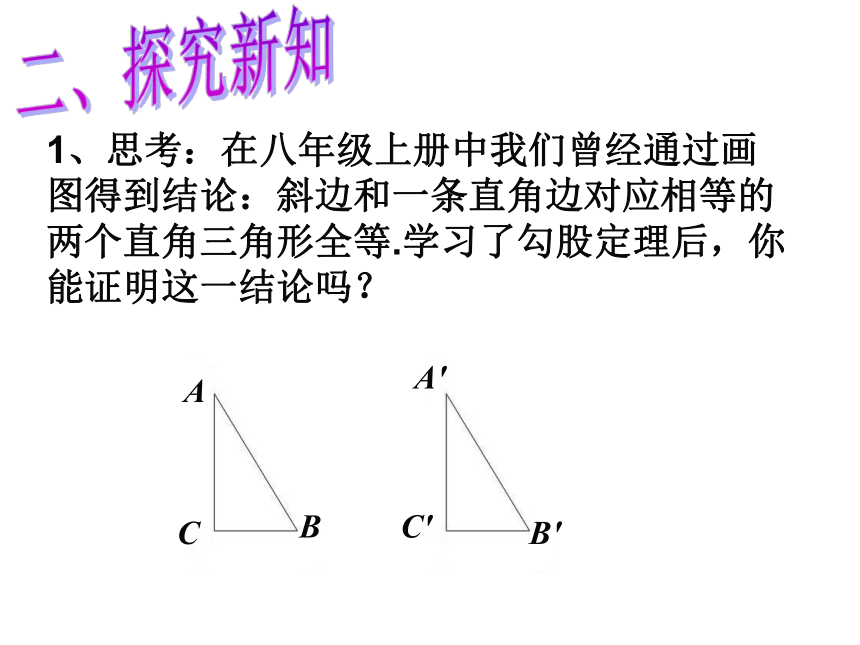
3. 叫做无理数.a2+b2=c2无限不循环小数 一、复习引入1、思考:在八年级上册中我们曾经通过画图得到结论:斜边和一条直角边对应相等的两个直角三角形全等.学习了勾股定理后,你能证明这一结论吗? 二、探究新知已知:如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,? AB=A′B′,? AC=A′C′.
求证:△ABC≌△ A′B′C′ .证明: ∵在Rt△ABC和Rt△A′B′C′中, ∠C=∠C′=90°,
∴BC2=AB2-AC2,B′C′ 2= A′B′ 2- A′C′ 2.
∵AB= A′B′ ,?AC= A′C′ ,
∴BC2= B′C′ 2,
∴BC= B′C′ .
在△ABC和△ A′B′C′中,
∵∠C=∠C′ , AC= A′C′ , BC= B′C′,
∴△ABC≌△ A′B′C′.
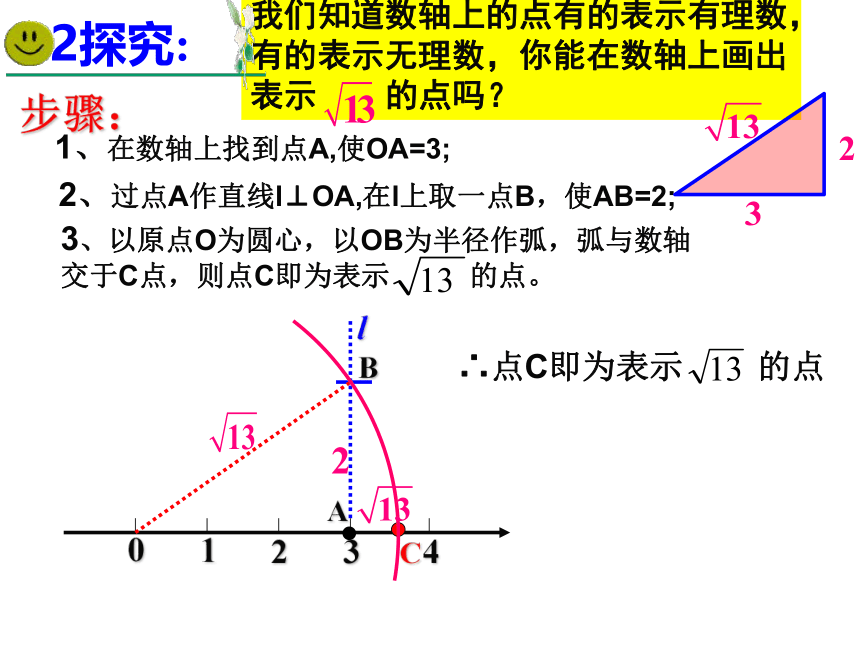
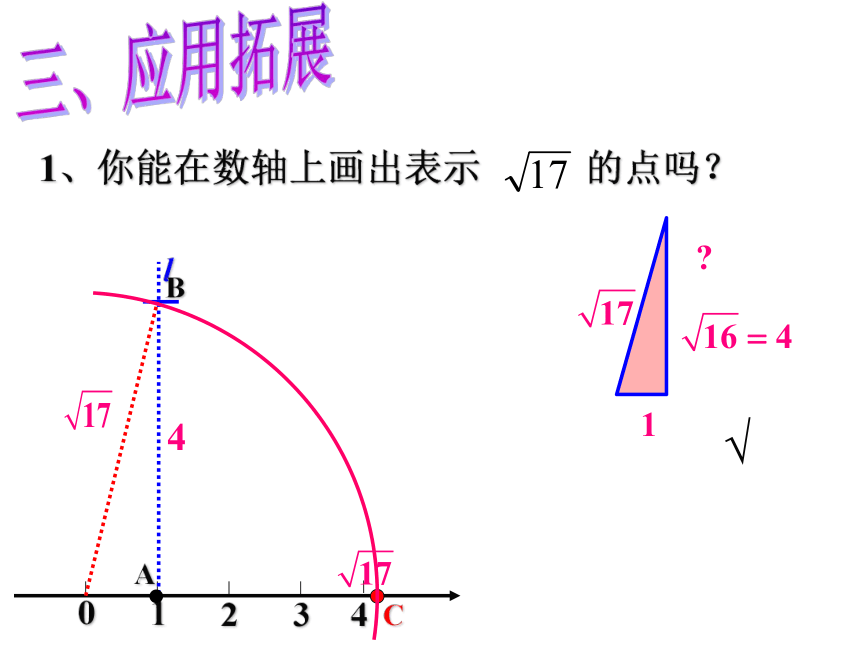
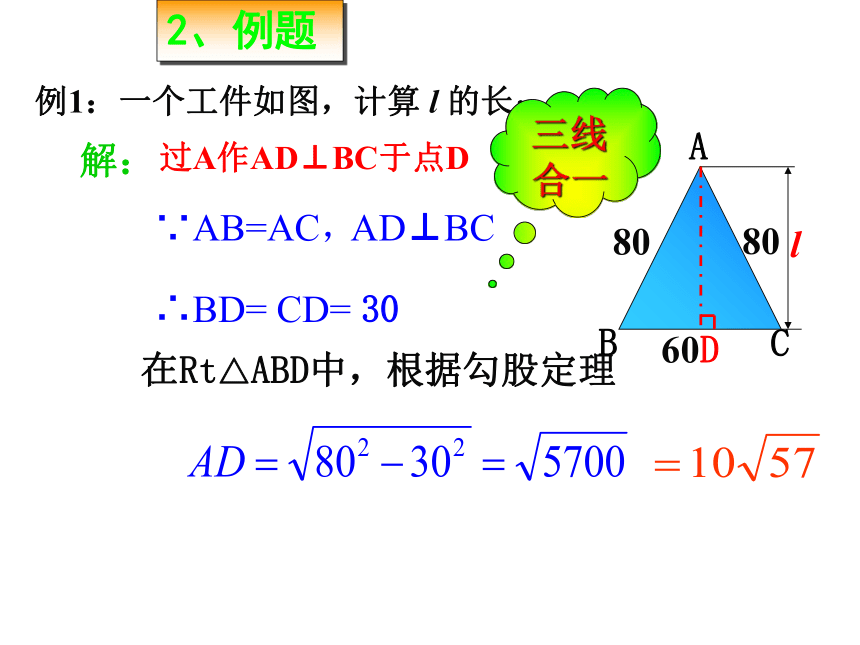
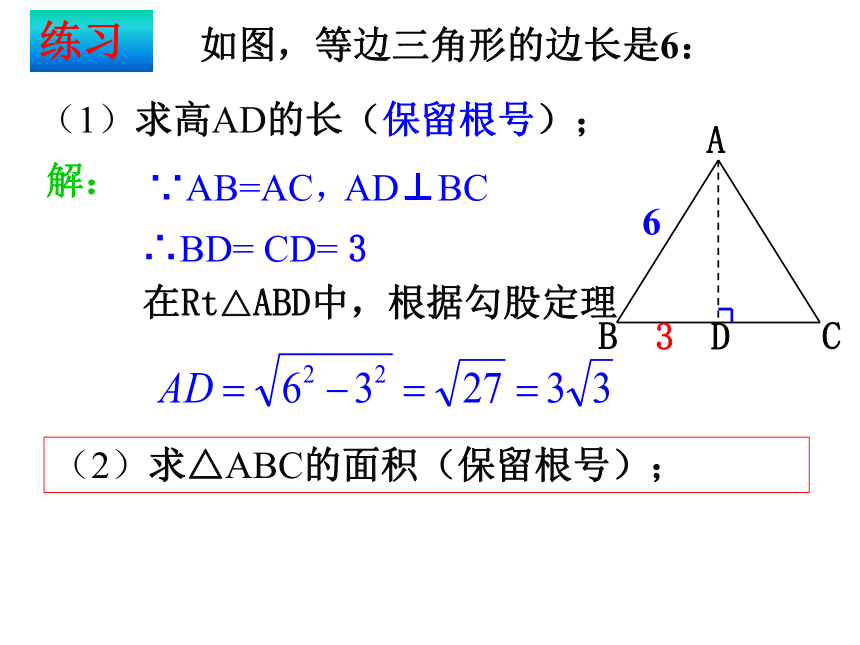
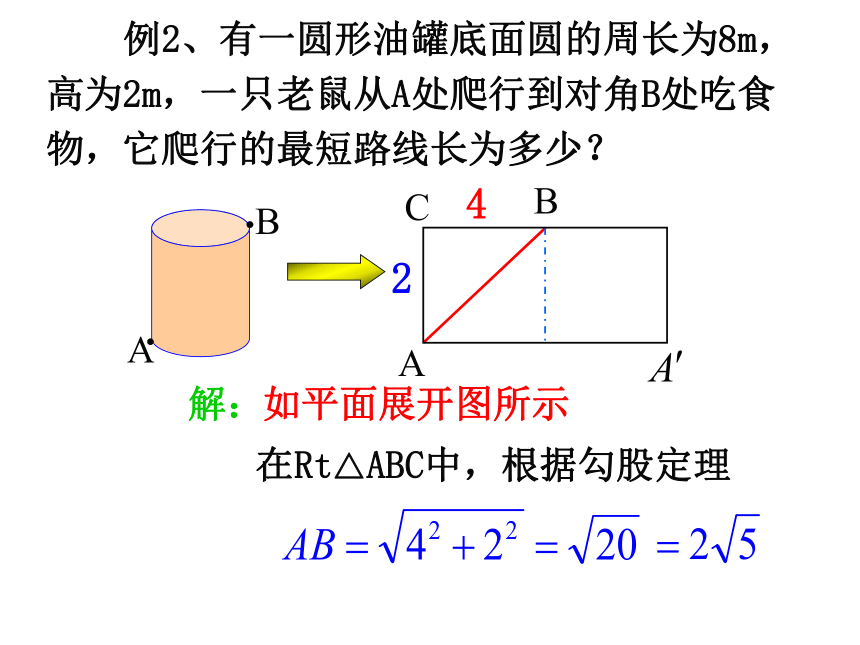
?????????01234步骤:lABC1、在数轴上找到点A,使OA=3;2、过点A作直线l⊥OA,在l上取一点B,使AB=2;3、以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,则点C即为表示 的点。∴点C即为表示 的点我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示 的点吗?2探究:01234lABC1、你能在数轴上画出表示 的点吗?√三、应用拓展2、例题CBA例1:一个工件如图,计算 l 的长:D80解:过A作AD⊥BC于点D∵AB=AC,AD⊥BC∴BD= CD= 30在Rt△ABD中,根据勾股定理三线合一D36CBA如图,等边三角形的边长是6:练习(1)求高AD的长(保留根号);(2)求△ABC的面积(保留根号);解:∵AB=AC,AD⊥BC∴BD= CD= 3在Rt△ABD中,根据勾股定理 例2、有一圆形油罐底面圆的周长为8m,高为2m,一只老鼠从A处爬行到对角B处吃食物,它爬行的最短路线长为多少?CB24解:如平面展开图所示在Rt△ABC中,根据勾股定理你能在数轴上表示出 的点吗?√√在数学中也有这样一幅美丽的“海螺型”图案由此可知,利用勾股定理,可以作出长为
111111111111111111第七届国际数学
教育大会的会徽1数学海螺图:你能在数轴上表示出
的点吗?的线段.1、如图为4×4的正方形网格,以格点与点A为端点,你能画出几条边长为 的线段?达标检测2.已知等腰三角形的一条腰长是5,底边长是6,则它底边上的高为 .
3 .长为 的线段是直角边长为正整数 , 的直角三角形的斜边.
4.如图所示,在正方形网格中,每个小正方形的边长为1,则在网格上的三角形ABC中,边长为无理数的边数为( )
A.0 B.1 C.2 D.3
5.如图所示,等边三角形ABC的边长为8.(1)求高AD的长;
(2)求这个三角形的面积(答案可保留根号).C1546.如图,D(2,1),以OD为一边画等腰三角形,并且使另一个顶点在x轴上,这样的等腰三角形能画多少个?写出落在x轴上的顶点坐标.OD⌒CEFHxy7、荷花问题
平平湖水清可鉴,
面上半尺生红莲;
出泥不染亭亭立,
忽被强风吹一边;
渔人观看忙向前,
花离原位二尺远;
能算诸君请解题,
湖水如何知深浅. 0.5xx+0.52答:湖水深3.75尺.可用勾股定理建立方程.8、如图,是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?BA55cm10cm6cm55cm48cm解题思路:把握题意——找关键字词——连接相关知识——建立数学模型(建模)9.如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是( ).
(A)3 (B )√ 5 (C)2 (D)1分析: 由于蚂蚁是沿正方体的外表面爬行的,
故需把正方体展开成平面图形(如图).B10.如图,在△ABC中,∠A=150°,AB=20 cm,AC=30 cm,则△ABC的面积 等于( ????).? A.450 cm2 ????B.300 cm2 C.330 cm2 ????D.150 cm2 ? ∵∠BAC=150°,∴∠DAC=30°.在Rt△ACD中,∠DAC=30°,∴CD=?AC=?×30=15(cm).∴S△ABC=?AB·CD=?×20×15=150(cm2),故选D.答案:D解析:过点C作CD⊥AB,垂足为D,构造特殊的直角三角形如图,在四边形ABCD中,AB=2,CD=1,∠A=60°,∠B=∠D=90°,
求四边形ABCD的面积.解:如图所示,延长AD,BC相交于点E,∵∠A=60°,∠B=90°,∴∠E=30°.在Rt△CDE中,∠CDE=90°,CD=1,∴CE=2.DE=? = =?.故S△CDE=?CD·DE=?×1× ?=?.在Rt△ABE中,∠ABE=90°,∠E=30°,∴AE=2AB=2×2=4,BE=? = =2?.∴S△ABE=? AB·BE=?×2×2?=2?.∴S四边形ABCD=S△ABE-S△CDE=2?-?=??.点拨:求不规则图形的面积,关键是用割补法将其转化为规则图形,然 后再求其面积.作业:
习题17.1 第6题,第7题
17.1 勾股定理(3)藤县太平四中
莫素芳1.已知直角三角形ABC的三边为a、b、c , ∠C= 90°,则 a、b、c 三者之间的关系是 ;
2.若一个直角三角形两条直角边长是3和2,那么第三条边长是 ;
3. 叫做无理数.a2+b2=c2无限不循环小数 一、复习引入1、思考:在八年级上册中我们曾经通过画图得到结论:斜边和一条直角边对应相等的两个直角三角形全等.学习了勾股定理后,你能证明这一结论吗? 二、探究新知已知:如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,? AB=A′B′,? AC=A′C′.
求证:△ABC≌△ A′B′C′ .证明: ∵在Rt△ABC和Rt△A′B′C′中, ∠C=∠C′=90°,
∴BC2=AB2-AC2,B′C′ 2= A′B′ 2- A′C′ 2.
∵AB= A′B′ ,?AC= A′C′ ,
∴BC2= B′C′ 2,
∴BC= B′C′ .
在△ABC和△ A′B′C′中,
∵∠C=∠C′ , AC= A′C′ , BC= B′C′,
∴△ABC≌△ A′B′C′.
?????????01234步骤:lABC1、在数轴上找到点A,使OA=3;2、过点A作直线l⊥OA,在l上取一点B,使AB=2;3、以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,则点C即为表示 的点。∴点C即为表示 的点我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示 的点吗?2探究:01234lABC1、你能在数轴上画出表示 的点吗?√三、应用拓展2、例题CBA例1:一个工件如图,计算 l 的长:D80解:过A作AD⊥BC于点D∵AB=AC,AD⊥BC∴BD= CD= 30在Rt△ABD中,根据勾股定理三线合一D36CBA如图,等边三角形的边长是6:练习(1)求高AD的长(保留根号);(2)求△ABC的面积(保留根号);解:∵AB=AC,AD⊥BC∴BD= CD= 3在Rt△ABD中,根据勾股定理 例2、有一圆形油罐底面圆的周长为8m,高为2m,一只老鼠从A处爬行到对角B处吃食物,它爬行的最短路线长为多少?CB24解:如平面展开图所示在Rt△ABC中,根据勾股定理你能在数轴上表示出 的点吗?√√在数学中也有这样一幅美丽的“海螺型”图案由此可知,利用勾股定理,可以作出长为
111111111111111111第七届国际数学
教育大会的会徽1数学海螺图:你能在数轴上表示出
的点吗?的线段.1、如图为4×4的正方形网格,以格点与点A为端点,你能画出几条边长为 的线段?达标检测2.已知等腰三角形的一条腰长是5,底边长是6,则它底边上的高为 .
3 .长为 的线段是直角边长为正整数 , 的直角三角形的斜边.
4.如图所示,在正方形网格中,每个小正方形的边长为1,则在网格上的三角形ABC中,边长为无理数的边数为( )
A.0 B.1 C.2 D.3
5.如图所示,等边三角形ABC的边长为8.(1)求高AD的长;
(2)求这个三角形的面积(答案可保留根号).C1546.如图,D(2,1),以OD为一边画等腰三角形,并且使另一个顶点在x轴上,这样的等腰三角形能画多少个?写出落在x轴上的顶点坐标.OD⌒CEFHxy7、荷花问题
平平湖水清可鉴,
面上半尺生红莲;
出泥不染亭亭立,
忽被强风吹一边;
渔人观看忙向前,
花离原位二尺远;
能算诸君请解题,
湖水如何知深浅. 0.5xx+0.52答:湖水深3.75尺.可用勾股定理建立方程.8、如图,是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?BA55cm10cm6cm55cm48cm解题思路:把握题意——找关键字词——连接相关知识——建立数学模型(建模)9.如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是( ).
(A)3 (B )√ 5 (C)2 (D)1分析: 由于蚂蚁是沿正方体的外表面爬行的,
故需把正方体展开成平面图形(如图).B10.如图,在△ABC中,∠A=150°,AB=20 cm,AC=30 cm,则△ABC的面积 等于( ????).? A.450 cm2 ????B.300 cm2 C.330 cm2 ????D.150 cm2 ? ∵∠BAC=150°,∴∠DAC=30°.在Rt△ACD中,∠DAC=30°,∴CD=?AC=?×30=15(cm).∴S△ABC=?AB·CD=?×20×15=150(cm2),故选D.答案:D解析:过点C作CD⊥AB,垂足为D,构造特殊的直角三角形如图,在四边形ABCD中,AB=2,CD=1,∠A=60°,∠B=∠D=90°,
求四边形ABCD的面积.解:如图所示,延长AD,BC相交于点E,∵∠A=60°,∠B=90°,∴∠E=30°.在Rt△CDE中,∠CDE=90°,CD=1,∴CE=2.DE=? = =?.故S△CDE=?CD·DE=?×1× ?=?.在Rt△ABE中,∠ABE=90°,∠E=30°,∴AE=2AB=2×2=4,BE=? = =2?.∴S△ABE=? AB·BE=?×2×2?=2?.∴S四边形ABCD=S△ABE-S△CDE=2?-?=??.点拨:求不规则图形的面积,关键是用割补法将其转化为规则图形,然 后再求其面积.作业:
习题17.1 第6题,第7题
