人教版数学8年级上册 《第十二章 全等三角形》学案
文档属性
| 名称 | 人教版数学8年级上册 《第十二章 全等三角形》学案 |  | |
| 格式 | docx | ||
| 文件大小 | 149.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-13 15:20:40 | ||
图片预览


文档简介
《第十二章 全等三角形》学案
一、阅读课本,回忆知识点
考点1 全等三角形的定义及性质
定义:能够 的两个三角形叫做全等三角形。
性质:1.全等三角形中,对应边 ,对应角 。(对边、对角的区别)
2.全等三角形的对应线段(对应边上的中线,对应边上的高,对应角的平分线)__ 。
3.全等三角形的周长 ,面积 。
考点2 全等三角形的判定
一般图形:
1.“边边边”( ): 分别相等的两个三角形全等。
2.“边角边”( ): 分别相等的两个三角形全等。
3.“角边角”( ): 分别相等的两个三角形全等。
4.“角角边”( ): 分别相等的两个三角形全等。
全等三角形的证明思路:
(1)已知两边:①找 →SAS ②找 →SSS
(2)已知一边一角:
①边角相对→找另外任一角→
②边角相邻→
考点3 直角三角形的判定
全等三角形的判定:(1)一般三角形全等的判定: 。
(2)直角三角形全等的判定: 。
考点4 角的平分线的性质和判定(如上图)
1.角的平分线的性质定理是___________________。符号语言
2.角的平分线的判定定理是___________________。符号语言
温馨提示:证明两条线段相等或两个角相等以及两条线平行时,通常通过证明全等得到答案。证明两个三角形全等,必须要有一对边相等,否则不能得到全等。
考点5 全等三角形的综合应用
利用全等三角形可以测出不能(或不易)直接测量长度的线段长,例如,河宽,或利用全等测量小口瓶的内径等。
基础训练
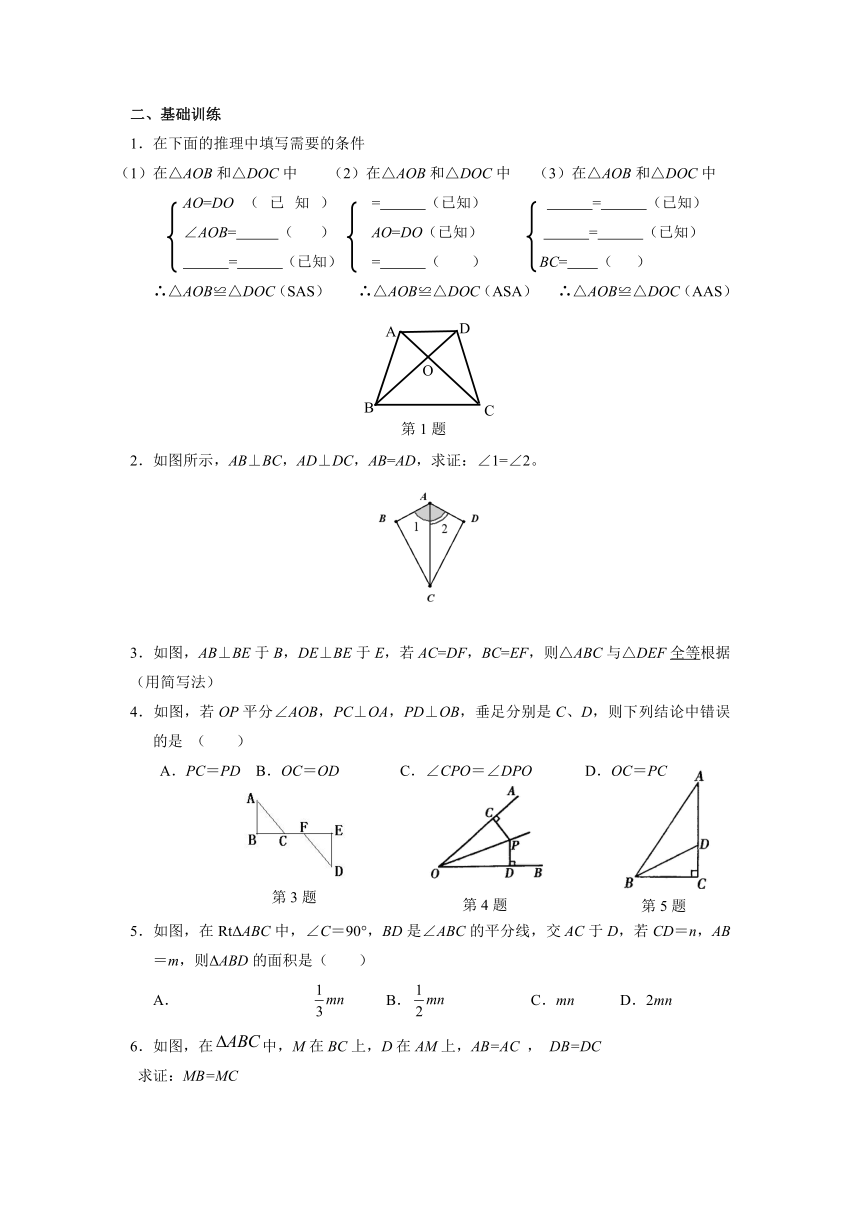
1.在下面的推理中填写需要的条件
(1)在△AOB和△DOC中 (2)在△AOB和△DOC中 (3)在△AOB和△DOC中
AO=DO(已知) = (已知) = (已知)
∠AOB= ( ) AO=DO(已知) = (已知)
= (已知) = ( ) BC= ( )
∴△AOB≌△DOC(SAS) ∴△AOB≌△DOC(ASA) ∴△AOB≌△DOC(AAS)
2.如图所示,AB⊥BC,AD⊥DC,AB=AD,求证:∠1=∠2。
3.如图,AB⊥BE于B,DE⊥BE于E,若AC=DF,BC=EF,则△ABC与△DEF全等根据 (用简写法)
4.如图,若OP平分∠AOB,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论中错误的是 ( )
(
第
5
题
第
4
题
第
3
题
) A.PC=PD B.OC=OD C.∠CPO=∠DPO D.OC=PC
5.如图,在RtΔABC中,∠C=90°,BD是∠ABC的平分线,交AC于D,若CD=n,AB=m,则ΔABD的面积是( )
B. C.mn D.2mn
6.如图,在中,M在BC上,D在AM上,AB=AC , DB=DC
求证:MB=MC
7.如图:AD=EB, BF=DG, BF∥DG,点A、B、C、D、E在同一直线上。求证: AF=EG。
8.如图,在中,AB=AC,D、E分别在BC、AC边上。且,AD=DE
求证:≌.
三、例题讲解
例1 如图,已知:∠B=∠C=90°,M是BC的中点,DM平分∠ADC.
求证:(1)AM平分∠DAB;(2)AD=AB+CD.
例2 两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.(8分)
(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)证明:DC⊥BE
例3 有下列论断(1)DE=CE(2)∠1=∠2(3)∠3=∠4,请以其中两个作为条件,另一个作为结论,写出一个真命题,并加以证明.
已知:如图
求证:
证明:
例4 如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG。
求证:(1)AD=AG,(2)AD与AG的位置关系如何 说明理由
四、反思小结,提炼知识点
我的收获:
我的疑问:
五、当堂反馈,检测知识点
(
A
D
F
C
B
E
第
1
题图
第
2
题图
第
3
题图
第
5
题图
第
4
题图
第
6
题图
)1.如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件: ,使△AEH≌△CEB.
2.如图,把一张矩形纸片ABCD沿BD对折,使C点落在E处,BE与AD相交于点O,写出一组相等的线段 (不包括AB=CD和AD=BC).
3.如图,∠E=∠F=900,∠B=∠C,AE=AF.给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中正确的结论是 (填序号).
4.如图所示,△ABC中,AB=BC=AC,∠B=∠C=60°,BD=CE,AD与BE相交于点P,则∠APE的度数是( )
A.45° B.55° C.75° D.60°
5.如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB, P、Q两点分别在AC和AC的垂线AX上移动,则当AP= 时,才能使△ABC和△APQ全等.
6.如图,有一块边长为4的正方形塑料摸板ABCD,将一块足够大的直角三角板的直角顶点落在A点,两条直角边分别与CD交于点F,与CB延长线交于点E.则四边形AECF的面积是
7.已知:如图,OD平分∠POQ,在OP、OQ边上取OA=OB,点C在OD上,CM⊥AD于M,CN⊥BD于N.求证:CM=CN.
8.如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC。求证:(1)EC=BF;(2)EC⊥BF
一、阅读课本,回忆知识点
考点1 全等三角形的定义及性质
定义:能够 的两个三角形叫做全等三角形。
性质:1.全等三角形中,对应边 ,对应角 。(对边、对角的区别)
2.全等三角形的对应线段(对应边上的中线,对应边上的高,对应角的平分线)__ 。
3.全等三角形的周长 ,面积 。
考点2 全等三角形的判定
一般图形:
1.“边边边”( ): 分别相等的两个三角形全等。
2.“边角边”( ): 分别相等的两个三角形全等。
3.“角边角”( ): 分别相等的两个三角形全等。
4.“角角边”( ): 分别相等的两个三角形全等。
全等三角形的证明思路:
(1)已知两边:①找 →SAS ②找 →SSS
(2)已知一边一角:
①边角相对→找另外任一角→
②边角相邻→
考点3 直角三角形的判定
全等三角形的判定:(1)一般三角形全等的判定: 。
(2)直角三角形全等的判定: 。
考点4 角的平分线的性质和判定(如上图)
1.角的平分线的性质定理是___________________。符号语言
2.角的平分线的判定定理是___________________。符号语言
温馨提示:证明两条线段相等或两个角相等以及两条线平行时,通常通过证明全等得到答案。证明两个三角形全等,必须要有一对边相等,否则不能得到全等。
考点5 全等三角形的综合应用
利用全等三角形可以测出不能(或不易)直接测量长度的线段长,例如,河宽,或利用全等测量小口瓶的内径等。
基础训练
1.在下面的推理中填写需要的条件
(1)在△AOB和△DOC中 (2)在△AOB和△DOC中 (3)在△AOB和△DOC中
AO=DO(已知) = (已知) = (已知)
∠AOB= ( ) AO=DO(已知) = (已知)
= (已知) = ( ) BC= ( )
∴△AOB≌△DOC(SAS) ∴△AOB≌△DOC(ASA) ∴△AOB≌△DOC(AAS)
2.如图所示,AB⊥BC,AD⊥DC,AB=AD,求证:∠1=∠2。
3.如图,AB⊥BE于B,DE⊥BE于E,若AC=DF,BC=EF,则△ABC与△DEF全等根据 (用简写法)
4.如图,若OP平分∠AOB,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论中错误的是 ( )
(
第
5
题
第
4
题
第
3
题
) A.PC=PD B.OC=OD C.∠CPO=∠DPO D.OC=PC
5.如图,在RtΔABC中,∠C=90°,BD是∠ABC的平分线,交AC于D,若CD=n,AB=m,则ΔABD的面积是( )
B. C.mn D.2mn
6.如图,在中,M在BC上,D在AM上,AB=AC , DB=DC
求证:MB=MC
7.如图:AD=EB, BF=DG, BF∥DG,点A、B、C、D、E在同一直线上。求证: AF=EG。
8.如图,在中,AB=AC,D、E分别在BC、AC边上。且,AD=DE
求证:≌.
三、例题讲解
例1 如图,已知:∠B=∠C=90°,M是BC的中点,DM平分∠ADC.
求证:(1)AM平分∠DAB;(2)AD=AB+CD.
例2 两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.(8分)
(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)证明:DC⊥BE
例3 有下列论断(1)DE=CE(2)∠1=∠2(3)∠3=∠4,请以其中两个作为条件,另一个作为结论,写出一个真命题,并加以证明.
已知:如图
求证:
证明:
例4 如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG。
求证:(1)AD=AG,(2)AD与AG的位置关系如何 说明理由
四、反思小结,提炼知识点
我的收获:
我的疑问:
五、当堂反馈,检测知识点
(
A
D
F
C
B
E
第
1
题图
第
2
题图
第
3
题图
第
5
题图
第
4
题图
第
6
题图
)1.如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件: ,使△AEH≌△CEB.
2.如图,把一张矩形纸片ABCD沿BD对折,使C点落在E处,BE与AD相交于点O,写出一组相等的线段 (不包括AB=CD和AD=BC).
3.如图,∠E=∠F=900,∠B=∠C,AE=AF.给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中正确的结论是 (填序号).
4.如图所示,△ABC中,AB=BC=AC,∠B=∠C=60°,BD=CE,AD与BE相交于点P,则∠APE的度数是( )
A.45° B.55° C.75° D.60°
5.如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB, P、Q两点分别在AC和AC的垂线AX上移动,则当AP= 时,才能使△ABC和△APQ全等.
6.如图,有一块边长为4的正方形塑料摸板ABCD,将一块足够大的直角三角板的直角顶点落在A点,两条直角边分别与CD交于点F,与CB延长线交于点E.则四边形AECF的面积是
7.已知:如图,OD平分∠POQ,在OP、OQ边上取OA=OB,点C在OD上,CM⊥AD于M,CN⊥BD于N.求证:CM=CN.
8.如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC。求证:(1)EC=BF;(2)EC⊥BF
