北京市第一七一中学2023-2024学年高二上学期期中调研数学试题(PDF版无答案)
文档属性
| 名称 | 北京市第一七一中学2023-2024学年高二上学期期中调研数学试题(PDF版无答案) |  | |
| 格式 | |||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-11 21:19:56 | ||
图片预览


文档简介
北京市2023—2024 学年度第一学期
高二年级数学科目 期中调研试题
(时长:120 分钟 总分值:150 分 )
第一部分(选择题 共 40分)
一、填空题(每小题 4 分,共 40 分)
2 2
1. 圆 x y 2x 4y 3 0的圆心为( ).
A. (1, 2) B. ( 1, 2) C. (2, 4) D. ( 2,4)
2. 若直线 l1 : x y 1 0与 l2 : x ay 1 0垂直,则实数 a=( )
A. 1 B. 2 C. 3 D. 1
2
3. x若椭圆 y2 1上一点 P到椭圆一个焦点的距离为 6,则 P到另一个焦点的距离为( )
25
A. 3 B. 4 C. 5 D. 6
4. 已知空间向量m (3,1,3),n ( 1, , 1),且m / /n,则实数 ( )
1 1
A. B. 3 C. D. 6
3 3
5. 已知直线 ax y 2 a 0在两坐标轴上的截距相等,则实数a ( )
A. 1 B. 1 C. 2或 1 D. 2或 1
6. 直线 y x b与曲线 x 4 y2 有且仅有一个公共点,则实数 b的取值范围为( )
A. 2 2,2 2 B. 2,2 2 2
C. 2,2 2 2 2 D. 2,2 2 2
7. 已知四面体 A BCD的所有棱长都等于 2,E是棱 AB的中点,F是棱 CD靠近 C的四等分点,
则 EF AC等于( )
1 5 5
A. B. 12 C. D.2 2 2
1
{#{QQABIY6UggAgAAAAAAhCUwHwCEIQkBACAIoGwBAIsAABQQFABAA=}#}
8. 直线 l经过点 A(1,2),在 x轴上的截距的取值范围是(-3,3),则其斜率的取值范围是( )
A. 1
1 1
, B. , ∪(1,+∞)
5 2
1 + 1 C. (-∞,-1)∪ , D. (-∞,-1)∪ , 5 2
9. 直线 l1 : ax y b 0与 l2 :bx y a 0(其中 a 0,b 0, ≠b),在同一坐标系中的图
象是下图中的( )
A. B. C. D.
10. 如图,在正方体 ABCD A1B1C1D1中,M ,N 分别是棱 AB,BB1的中点,点 P在对角线CA1
上运动.当△PMN 的面积取得最小值时,点 P的位置是( )
A. 线段CA1的三等分点,且靠近点 A1
B. 线段CA1的中点
C. 线段CA1的三等分点,且靠近点C
D. 线段CA1的四等分点,且靠近点C
第二部分(非选择题 共 110分)
二、填空题(每小题 5 分,共 25 分)
11. 直线 x 1的倾斜角为___________.
12. 直线3x 2y a 0和直线3x 2y 1 0的位置关系是________.
13. 已知 i, j,k为空间两两垂直的单位向量,且 a 3i 2 j k ,b i j 2k , 则数量积
a b =_________________.
14. 若直线 x y m 0与圆 x2 y2 2相离,则m的取值范围是__________.
2
{#{QQABIY6UggAgAAAAAAhCUwHwCEIQkBACAIoGwBAIsAABQQFABAA=}#}
15. 在平面直角坐标系 xOy中,将直线 l沿 x轴正方向平移 3个单位长度,沿 y轴正方向平移 5个
单位长度,得到直线 l1 .再将直线 l1沿 x轴正方向平移 1个单位长度,沿 y轴负方向平移 2个单位
长度,又与直线 l重合.若直线 l与直线 l1关于点(2,3)对称,则直线 l的方程是________________.
三、解答题(本大题共 6 小题,满分 85 分)
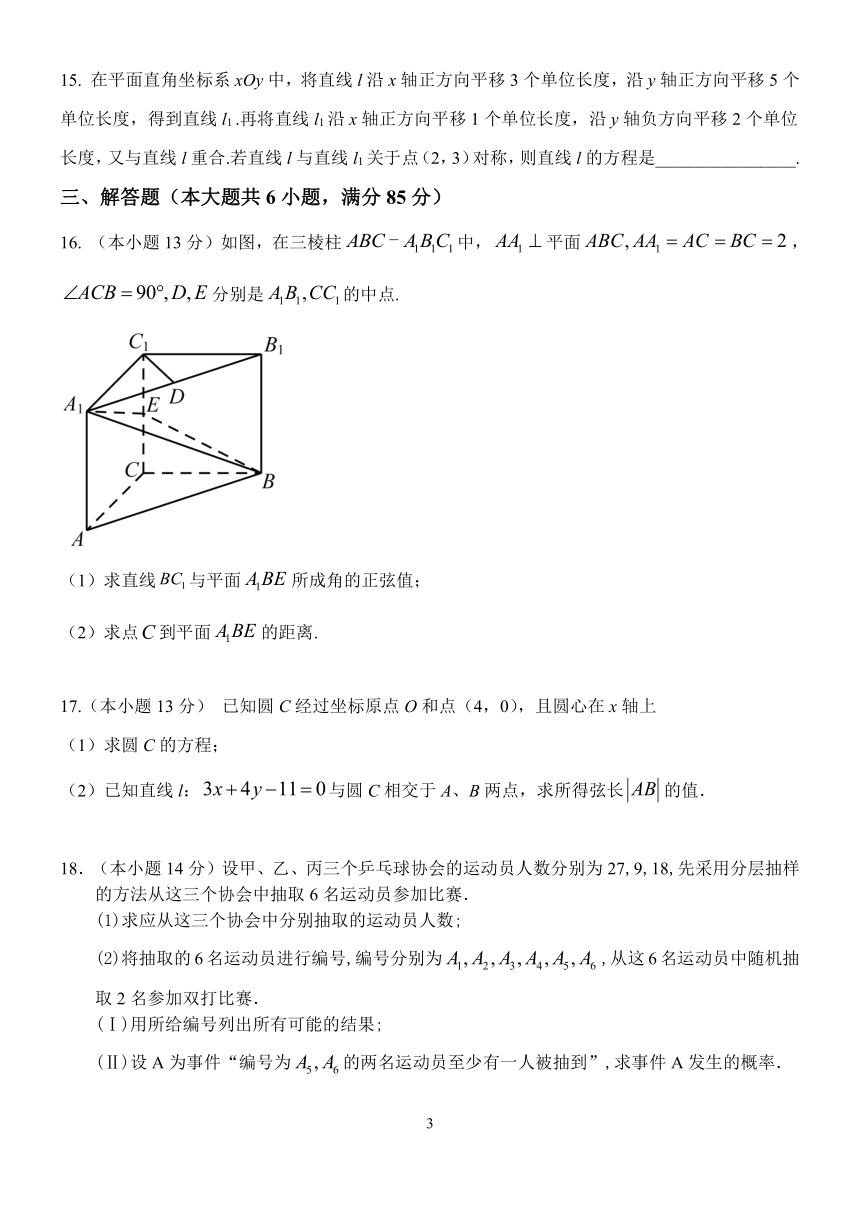
16. (本小题 13分)如图,在三棱柱 ABC - A1B1C1中, AA1 平面 ABC, AA1 AC BC 2,
ACB 90 ,D,E分别是 A1B1,CC1的中点.
(1)求直线 BC1与平面 A1BE 所成角的正弦值;
(2)求点C到平面 A1BE 的距离.
17.(本小题 13分) 已知圆 C经过坐标原点 O和点(4,0),且圆心在 x轴上
(1)求圆 C的方程;
(2)已知直线 l:3x 4y 11 0与圆 C相交于 A、B两点,求所得弦长 AB 的值.
18.(本小题 14分)设甲、乙、丙三个乒乓球协会的运动员人数分别为 27,9,18,先采用分层抽样
的方法从这三个协会中抽取 6名运动员参加比赛.
(1)求应从这三个协会中分别抽取的运动员人数;
(2)将抽取的 6名运动员进行编号,编号分别为 A1, A2 , A3 , A4 , A5 , A6 ,从这 6名运动员中随机抽
取 2名参加双打比赛.
(Ⅰ)用所给编号列出所有可能的结果;
(Ⅱ)设 A为事件“编号为 A5 , A6 的两名运动员至少有一人被抽到”,求事件 A发生的概率.
3
{#{QQABIY6UggAgAAAAAAhCUwHwCEIQkBACAIoGwBAIsAABQQFABAA=}#}
19. (本小题 15分)如图所示,四边形 ABCD是边长为 3的正方形,DE⊥平面 ABCD,AF //DE,
DE 3AF ,BE与平面 ABCD所成角为 60°.
(1)求证: AC 平面 BDE;
(2)求二面角 F BE D的余弦值;
(3)设点 M是线段 BD上的一个动点,试确定点 M的位置,使得 AM //平面 BEF,并证明你的
结论.
2 2
20(. 本小题 15分)已知椭C :
x y
圆2 2 2 1(a b 0)的左 右焦点分别为 F1,F2,其中右焦点坐标为 1,0 ,a b
1
该椭圆的离心率为 2 .
(1)求椭圆的标准方程;
(2)已知点P 1, t 为椭圆上一点,过点 F2的直线 l与椭圆交于异于点 P的 A,B两点,若△PAB的面积
9 2
是 ,求直线 l的方程.
7
4
{#{QQABIY6UggAgAAAAAAhCUwHwCEIQkBACAIoGwBAIsAABQQFABAA=}#}
21.(本小题 15分)“曼哈顿几何”也叫“出租车几何”,是在 19 世纪由赫尔曼·闵可夫斯基提出
来的.图 1 是抽象的城市路网,其中线段 AB 是欧式空间中定义的两点最短距离,但在城市路网
中,我们只能走有路的地方,不能“穿墙”而过,所以在“曼哈顿几何”中,这两点最短距离用 d (A,B)
表示,又称“曼哈顿距离”,即 d(A,B) AB CB ,因此
“曼哈顿两点间距离公式”:若 A x1, y1 ,B x2 , y2 ,则 d (A,B) x2 x1 y2 y1
图 1
(1) ①点 A 3,5 ,B 2, 1 ,求 d (A,B)的值.
②求圆心在原点,半径为 1 的“曼哈顿单位圆”方程.
(2) 已知点 B(1,0),直线 2x y 2 0,求 B点到直线的“曼哈顿距离”最小值;
(3)设三维空间 4个点为 Ai xi , yi , zi ,i 1,2,3,4,且 xi , yi , zi 0,1 .设其中所有两点“曼
哈顿距离”的平均值即 d ,求d 最大值,并列举最值成立时的一组坐标.
5
{#{QQABIY6UggAgAAAAAAhCUwHwCEIQkBACAIoGwBAIsAABQQFABAA=}#}
草 稿 纸
6
{#{QQABIY6UggAgAAAAAAhCUwHwCEIQkBACAIoGwBAIsAABQQFABAA=}#}
高二年级数学科目 期中调研试题
(时长:120 分钟 总分值:150 分 )
第一部分(选择题 共 40分)
一、填空题(每小题 4 分,共 40 分)
2 2
1. 圆 x y 2x 4y 3 0的圆心为( ).
A. (1, 2) B. ( 1, 2) C. (2, 4) D. ( 2,4)
2. 若直线 l1 : x y 1 0与 l2 : x ay 1 0垂直,则实数 a=( )
A. 1 B. 2 C. 3 D. 1
2
3. x若椭圆 y2 1上一点 P到椭圆一个焦点的距离为 6,则 P到另一个焦点的距离为( )
25
A. 3 B. 4 C. 5 D. 6
4. 已知空间向量m (3,1,3),n ( 1, , 1),且m / /n,则实数 ( )
1 1
A. B. 3 C. D. 6
3 3
5. 已知直线 ax y 2 a 0在两坐标轴上的截距相等,则实数a ( )
A. 1 B. 1 C. 2或 1 D. 2或 1
6. 直线 y x b与曲线 x 4 y2 有且仅有一个公共点,则实数 b的取值范围为( )
A. 2 2,2 2 B. 2,2 2 2
C. 2,2 2 2 2 D. 2,2 2 2
7. 已知四面体 A BCD的所有棱长都等于 2,E是棱 AB的中点,F是棱 CD靠近 C的四等分点,
则 EF AC等于( )
1 5 5
A. B. 12 C. D.2 2 2
1
{#{QQABIY6UggAgAAAAAAhCUwHwCEIQkBACAIoGwBAIsAABQQFABAA=}#}
8. 直线 l经过点 A(1,2),在 x轴上的截距的取值范围是(-3,3),则其斜率的取值范围是( )
A. 1
1 1
, B. , ∪(1,+∞)
5 2
1 + 1 C. (-∞,-1)∪ , D. (-∞,-1)∪ , 5 2
9. 直线 l1 : ax y b 0与 l2 :bx y a 0(其中 a 0,b 0, ≠b),在同一坐标系中的图
象是下图中的( )
A. B. C. D.
10. 如图,在正方体 ABCD A1B1C1D1中,M ,N 分别是棱 AB,BB1的中点,点 P在对角线CA1
上运动.当△PMN 的面积取得最小值时,点 P的位置是( )
A. 线段CA1的三等分点,且靠近点 A1
B. 线段CA1的中点
C. 线段CA1的三等分点,且靠近点C
D. 线段CA1的四等分点,且靠近点C
第二部分(非选择题 共 110分)
二、填空题(每小题 5 分,共 25 分)
11. 直线 x 1的倾斜角为___________.
12. 直线3x 2y a 0和直线3x 2y 1 0的位置关系是________.
13. 已知 i, j,k为空间两两垂直的单位向量,且 a 3i 2 j k ,b i j 2k , 则数量积
a b =_________________.
14. 若直线 x y m 0与圆 x2 y2 2相离,则m的取值范围是__________.
2
{#{QQABIY6UggAgAAAAAAhCUwHwCEIQkBACAIoGwBAIsAABQQFABAA=}#}
15. 在平面直角坐标系 xOy中,将直线 l沿 x轴正方向平移 3个单位长度,沿 y轴正方向平移 5个
单位长度,得到直线 l1 .再将直线 l1沿 x轴正方向平移 1个单位长度,沿 y轴负方向平移 2个单位
长度,又与直线 l重合.若直线 l与直线 l1关于点(2,3)对称,则直线 l的方程是________________.
三、解答题(本大题共 6 小题,满分 85 分)
16. (本小题 13分)如图,在三棱柱 ABC - A1B1C1中, AA1 平面 ABC, AA1 AC BC 2,
ACB 90 ,D,E分别是 A1B1,CC1的中点.
(1)求直线 BC1与平面 A1BE 所成角的正弦值;
(2)求点C到平面 A1BE 的距离.
17.(本小题 13分) 已知圆 C经过坐标原点 O和点(4,0),且圆心在 x轴上
(1)求圆 C的方程;
(2)已知直线 l:3x 4y 11 0与圆 C相交于 A、B两点,求所得弦长 AB 的值.
18.(本小题 14分)设甲、乙、丙三个乒乓球协会的运动员人数分别为 27,9,18,先采用分层抽样
的方法从这三个协会中抽取 6名运动员参加比赛.
(1)求应从这三个协会中分别抽取的运动员人数;
(2)将抽取的 6名运动员进行编号,编号分别为 A1, A2 , A3 , A4 , A5 , A6 ,从这 6名运动员中随机抽
取 2名参加双打比赛.
(Ⅰ)用所给编号列出所有可能的结果;
(Ⅱ)设 A为事件“编号为 A5 , A6 的两名运动员至少有一人被抽到”,求事件 A发生的概率.
3
{#{QQABIY6UggAgAAAAAAhCUwHwCEIQkBACAIoGwBAIsAABQQFABAA=}#}
19. (本小题 15分)如图所示,四边形 ABCD是边长为 3的正方形,DE⊥平面 ABCD,AF //DE,
DE 3AF ,BE与平面 ABCD所成角为 60°.
(1)求证: AC 平面 BDE;
(2)求二面角 F BE D的余弦值;
(3)设点 M是线段 BD上的一个动点,试确定点 M的位置,使得 AM //平面 BEF,并证明你的
结论.
2 2
20(. 本小题 15分)已知椭C :
x y
圆2 2 2 1(a b 0)的左 右焦点分别为 F1,F2,其中右焦点坐标为 1,0 ,a b
1
该椭圆的离心率为 2 .
(1)求椭圆的标准方程;
(2)已知点P 1, t 为椭圆上一点,过点 F2的直线 l与椭圆交于异于点 P的 A,B两点,若△PAB的面积
9 2
是 ,求直线 l的方程.
7
4
{#{QQABIY6UggAgAAAAAAhCUwHwCEIQkBACAIoGwBAIsAABQQFABAA=}#}
21.(本小题 15分)“曼哈顿几何”也叫“出租车几何”,是在 19 世纪由赫尔曼·闵可夫斯基提出
来的.图 1 是抽象的城市路网,其中线段 AB 是欧式空间中定义的两点最短距离,但在城市路网
中,我们只能走有路的地方,不能“穿墙”而过,所以在“曼哈顿几何”中,这两点最短距离用 d (A,B)
表示,又称“曼哈顿距离”,即 d(A,B) AB CB ,因此
“曼哈顿两点间距离公式”:若 A x1, y1 ,B x2 , y2 ,则 d (A,B) x2 x1 y2 y1
图 1
(1) ①点 A 3,5 ,B 2, 1 ,求 d (A,B)的值.
②求圆心在原点,半径为 1 的“曼哈顿单位圆”方程.
(2) 已知点 B(1,0),直线 2x y 2 0,求 B点到直线的“曼哈顿距离”最小值;
(3)设三维空间 4个点为 Ai xi , yi , zi ,i 1,2,3,4,且 xi , yi , zi 0,1 .设其中所有两点“曼
哈顿距离”的平均值即 d ,求d 最大值,并列举最值成立时的一组坐标.
5
{#{QQABIY6UggAgAAAAAAhCUwHwCEIQkBACAIoGwBAIsAABQQFABAA=}#}
草 稿 纸
6
{#{QQABIY6UggAgAAAAAAhCUwHwCEIQkBACAIoGwBAIsAABQQFABAA=}#}
同课章节目录
